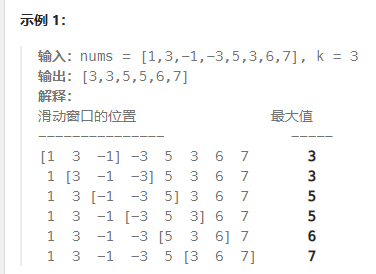
1.滑动窗口最大值
首先我们来回顾一下一个新的数据结构的理解: 单调队列
单调队列普遍是双端队列,且队列里的元素是单调递减的,这样就引申出了他的核心目的:
动态维护候选元素的最大值
- 单调队列的作用是在窗口滑动时,始终让队列头部是当前窗口的最大值下标;
- 为什么存的是下标呢,后来慢慢发现存下标能得到更多的信息,比如维护窗口长度
- 队尾是 "清理一窝":新元素来了,所有比它小的旧候选都没用了,得全清;
- 队首是 "清理一个":窗口挪一步,最多只漏出去一个队首元素,清一个就够。
- 因此入队用的是while,出队用的是if
用单调递减的结构:保证队首始终是当前窗口的最大值
每个元素只入队出队一次,相比暴力解法不断的滑动窗口,把 "求窗口最大值" 的时间从 O (k) 降到 O (1)
回到本题:
核心思路: 1.发现使用定长的单调队列完美解决这个需求
入队:枚举所有元素、如果新进元素比队列最后一个大,直接踢掉
出队:由于定长,超出长度时,踢掉老大
存储结果:当队列长度为3,就可以存储老大的值
每个元素只入队出队一次 时间复杂度O(n)
单调队列的空间开销由「窗口大小 k」决定,而非数组长度 n空间复杂度O(k)
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
ans = []
q = deque()
for i,x in enumerate(nums):
1.入队
while q and x>=nums[q[-1]]:
q.pop()
q.append(i)
2.出队
if i-q[0]+1>k:
q.popleft()
3.记录答案
if i+1>=k:
ans.append(nums[q[0]])
return ans2.最小覆盖子串

首先引入一个新的cnt的功能
比如目前有cnt_s=Counter(s) cnt_t=Counter(t)
cnt_s >= cnt_t:覆盖 简单说就是
cnt_s包含cnt_t所有字符的频次要求cnt_s={A:2 B:2 C:3····} cnt_t = {A:1 B:1 C:1}
可以直接比较
本题核心 1.变量 ans_left ans_right保存当前最好的结果
left right不断再更新窗口长度
if right - left < ans_right - ans_left:说明有更优解,更新
2.其他都是普通滑动窗口的模板
3.边界条件ans_left:初始就是-1,不存在的边界
只有当找到真正的有效覆盖子串 时,才会更新 ans_left 和 ans_right 为合法的下标
class Solution:
def minWindow(self, s: str, t: str) -> str:
m = len(s)
n = len(t)
ans_left = -1
ans_right = m
cnt_s = Counter()
cnt_t = Counter(t)
left = 0
for right,right_str in enumerate(s):
cnt_s[right_str]+=1
while cnt_s>=cnt_t:
if right-left<ans_right-ans_left:
ans_left,ans_right=left,right
cnt_s[s[left]]-=1
left+=1
if ans_left==-1:
return ''
else:
return s[ans_left:ans_right+1]