从根上了解一下复指数
作为一名通信小白,有一天看到实际链路中的数据都是复数,突然一根弦出现在脑海里,复数这玩意儿一开始到底是怎么产生的?遂查阅资料记录之。
文章目录
- 从根上了解一下复指数
-
- 1、虚数的来源-从解一元三次方程说起
- 2、从"虚"到"复":复数的正式确立(17-18世纪:代数与几何的双重认可)
-
- [2.1 笛卡尔的命名与复数的代数形式](#2.1 笛卡尔的命名与复数的代数形式)
- [2.2 高斯的复平面:复数的几何意义突破](#2.2 高斯的复平面:复数的几何意义突破)
- 3、指数的跨越:复指数函数的构建(18世纪:欧拉的大胆推广)
- 4、数学的"最美公式":欧拉公式的推导与意义(1748年)
-
- [4.1 欧拉公式的直接推导](#4.1 欧拉公式的直接推导)
- [4.2 欧拉公式的几何意义](#4.2 欧拉公式的几何意义)
- [4.3 欧拉公式的历史意义](#4.3 欧拉公式的历史意义)
- 5、总结:从"被迫妥协"到"主动构建"的数学思维跃迁
1、虚数的来源-从解一元三次方程说起
早在公元1世纪,古希腊数学家亚历山大的希罗考虑的是一种不可能的平顶金字塔的域积,计算结果会出现 81 − 144 \sqrt{81-144} 81−144 ,不过他觉得难以理解,放弃了继续研究。
16世纪中叶,意大利数学家卡尔达诺在其著作《大术》中,发表了三次代数方程一般解法的卡尔达诺公式(但真正发明此三次代数方程解法的为塔塔利亚,也是如此两人因而结怨。现代,人们已经习惯称呼的三次方程解法的"卡尔达诺公式",实际上应称呼为"塔塔利亚公式")。书中还记载了四次代数方程的一般解法(由他的学生费拉里发现)。尽管他成功得出正确的实数解,但虚数对他而言仅是"计算的中间过程",没有明确的实际意义,甚至被他称为"微不足道的数学怪物"。
为了方便理解,我们简单介绍一下这部分求根的内容:
初中数学学过根据求根公式解一元二次方程:
x = − b ± b 2 − 4 a c 2 a x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} x=2a−b±b2−4ac
根据 Δ = b 2 − 4 a c \Delta=b^2-4ac Δ=b2−4ac与0的关系分为有两个不同的解( Δ > 0 \Delta>0 Δ>0)、有两个相同的解( Δ = 0 \Delta=0 Δ=0)、无解( Δ < 0 \Delta<0 Δ<0)。当 b 2 − 4 a c < 0 b^2-4 a c<0 b2−4ac<0 时,根号下是负数,我们直接就说该方程无解。十六世纪的人们也是这么想的,因为对负数开根号没有数学意义。没解就是没解,对我们确实没有影响。
转折点出现在三次方程的求解上。十六世纪意大利数学家塔塔利亚给出了形如 x 3 = p x + q x^3=p x+q x3=px+q 的三次方程的公式:
x = q 2 + ( q 2 ) 2 − ( p 3 ) 3 3 + q 2 − ( q 2 ) 2 − ( p 3 ) 3 3 x=\sqrt[3]{\frac{q}{2}+\sqrt{\left(\frac{q}{2}\right)^2-\left(\frac{p}{3}\right)^3}}+\sqrt[3]{\frac{q}{2}-\sqrt{\left(\frac{q}{2}\right)^2-\left(\frac{p}{3}\right)^3}} x=32q+(2q)2−(3p)3 +32q−(2q)2−(3p)3
(推导过程以及一般形式的解参考文献 3 或参考文献 4,由于不是这篇文章的重点,不再详细介绍)
于是,一个示例三次方程 x 3 = 15 x + 4 x^3=15 x+4 x3=15x+4 的解就是:
x = 2 + 2 2 − 5 3 3 + 2 − 2 2 − 5 3 3 = 2 + 11 i 3 + 2 − 11 i 3 x=\sqrt[3]{2+\sqrt{2^2-5^3}}+\sqrt[3]{2-\sqrt{2^2-5^3}}=\sqrt[3]{2+11 i}+\sqrt[3]{2-11 i} x=32+22−53 +32−22−53 =32+11i +32−11i
可是 x = 4 x=4 x=4 就满足这个方程呀! 那 2 + 11 i 3 + 2 − 11 3 i \sqrt[3]{2+11 i}+\sqrt[3]{2-11} i 32+11i +32−11 i 又是什么情况?
卡尔达诺之后,意大利数学家邦贝利(Rafael Bombelli)在1572年出版的《代数学》中,对"负数的平方根"进行了系统研究。他发现,只要给这类数制定一套合理的运算规则,它们就能像实数一样进行加减乘除,并且能帮助解决三次方程的求解问题。
邦贝利首先定义了一个"虚数单位",用符号 i i i 表示(后世沿用此符号,由欧拉正式推广),规定 i = − 1 i = \sqrt{-1} i=−1 ,即 i 2 = − 1 i^2 = -1 i2=−1。在此基础上,他确立了虚数的基本运算规则:
- 加法: a i + b i = ( a + b ) i a i + b i = (a + b)i ai+bi=(a+b)i
- 减法: a i − b i = ( a − b ) i a i - b i = (a - b)i ai−bi=(a−b)i
- 乘法: i × i = − 1 i \times i = -1 i×i=−1, a i × b i = − a b a i \times b i = -ab ai×bi=−ab, ( a + b i ) ( c + d i ) = a c + a d i + b c i + b d i 2 = ( a c − b d ) + ( a d + b c ) i (a + b i)(c + d i) = ac + ad i + bc i + bd i^2 = (ac - bd) + (ad + bc)i (a+bi)(c+di)=ac+adi+bci+bdi2=(ac−bd)+(ad+bc)i(这已经是复数乘法的雏形)
邦贝利用这套规则重新计算了方程 x 3 = 15 x + 4 x^3 = 15x + 4 x3=15x+4 的根,他假设 2 + − 121 3 = a + b i \sqrt[3]{2 + \sqrt{-121}} = a + b i 32+−121 =a+bi, 2 − − 121 3 = a − b i \sqrt[3]{2 - \sqrt{-121}} = a - b i 32−−121 =a−bi(对称性假设,因为两个立方根的实数部分相同,虚数部分相反),代入后通过运算解得 a = 2 a = 2 a=2, b = 1 b = 1 b=1,因此:
2 + − 121 3 = 2 + i , 2 − − 121 3 = 2 − i \sqrt[3]{2 + \sqrt{-121}} = 2 + i,\sqrt[3]{2 - \sqrt{-121}} = 2 - i 32+−121 =2+i,32−−121 =2−i
两者相加得到 x = ( 2 + i ) + ( 2 − i ) = 4 x = (2 + i) + (2 - i) = 4 x=(2+i)+(2−i)=4,与真实根完全一致。
邦贝利的工作让"虚数"从一个"诡辩的符号"变成了一套可操作的运算体系。他虽然仍未理解虚数的几何意义,但至少证明了虚数在代数运算中的有效性。这是虚数发展史上的第一个关键突破。
这里我将其划分为第一阶段,在这个阶段中, − 1 \sqrt{-1} −1 看起来并无实际意义,只是一个让代数计算闭合的中间计算附属品。
2、从"虚"到"复":复数的正式确立(17-18世纪:代数与几何的双重认可)
2.1 笛卡尔的命名与复数的代数形式
17世纪,笛卡尔(René Descartes)在1637年的《几何学》中,首次将"负数的平方根"命名为"虚数"(imaginary number),意为"想象中的数";同时将我们熟悉的正数、负数、零、无理数称为"实数"(real number)。这一命名沿用至今。笛卡尔认为虚数只是数学世界中的一种抽象概念,缺乏实际应用价值。笛卡尔虽然指出了虚数的存在,但认为它是无法被理解的数学幻想。笛卡尔还提出了"复数"的雏形------他发现,当解二次方程 x 2 + b x + c = 0 x^2 + bx + c = 0 x2+bx+c=0 时,若判别式小于0,根可以表示为 x = − b 2 ± − ( b 2 4 − c ) x = -\frac{b}{2} \pm \sqrt{-\left(\frac{b^2}{4} - c\right)} x=−2b±−(4b2−c) ,即"实数部分 + 虚数部分"的形式。但笛卡尔并未将这种"实数+虚数"的组合视为一个独立的"数",而是将其看作两个分离的部分。
直到18世纪初,数学家们才逐渐意识到,"实数+虚数"的组合应该是一个完整的、不可分割的数。瑞士数学家欧拉(Leonhard Euler)在1732年的论文中,正式使用 a + b i a + b i a+bi 表示这类数(其中 a a a、 b b b 为实数, i i i 为虚数单位),并将其称为"复数"(complex number)。欧拉明确指出:复数 a + b i a + b i a+bi 是一个独立的数,其运算规则遵循邦贝利确立的法则。
此时,复数的代数体系已基本成型:
- 复数的一般形式: z = a + b i z = a + b i z=a+bi( a a a 为实部,记为 R e ( z ) Re(z) Re(z); b b b 为虚部,记为 I m ( z ) Im(z) Im(z))
- 相等关系: a + b i = c + d i ⟺ a = c a + b i = c + d i \iff a = c a+bi=c+di⟺a=c 且 b = d b = d b=d
- 四则运算:加法 ( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i (a + b i) + (c + d i) = (a + c) + (b + d)i (a+bi)+(c+di)=(a+c)+(b+d)i;减法 ( a + b i ) − ( c + d i ) = ( a − c ) + ( b − d ) i (a + b i) - (c + d i) = (a - c) + (b - d)i (a+bi)−(c+di)=(a−c)+(b−d)i;乘法 ( a + b i ) ( c + d i ) = ( a c − b d ) + ( a d + b c ) i (a + b i)(c + d i) = (ac - bd) + (ad + bc)i (a+bi)(c+di)=(ac−bd)+(ad+bc)i;除法 a + b i c + d i = ( a + b i ) ( c − d i ) c 2 + d 2 = a c + b d c 2 + d 2 + b c − a d c 2 + d 2 i \frac{a + b i}{c + d i} = \frac{(a + b i)(c - d i)}{c^2 + d^2} = \frac{ac + bd}{c^2 + d^2} + \frac{bc - ad}{c^2 + d^2}i c+dia+bi=c2+d2(a+bi)(c−di)=c2+d2ac+bd+c2+d2bc−adi(分母实数化)
2.2 高斯的复平面:复数的几何意义突破
尽管复数的代数运算体系已完善,但18世纪末之前,数学家仍对复数的"真实性"存疑------毕竟"虚数"的名字自带"想象"色彩,人们无法在现实世界中找到直观载体。事实上,在高斯正式提出复平面概念之前,已有多位学者为复数的几何表示付出了探索努力,只是未能形成系统理论或获得广泛认可。这种对复数几何意义的持续探索,直到高斯(Carl Friedrich Gauss)提出"复平面"概念后才完成关键突破,彻底消除了人们的质疑。
追溯复数几何表示的早期探索,最早可至17世纪末的英国数学家沃利斯(John Wallis)。作为牛顿之前英国最具影响力的数学家之一,沃利斯始终致力于为"不可直观"的数学概念寻找几何依托,1673年他在《代数论》(Treatise of Algebra)中专门开辟章节探讨虚数的几何解释,这也是数学史上首次系统性尝试为虚数赋予"实体"意义。他的核心思路是突破"实数仅对应数轴上点"的传统认知,提出在平面直角坐标系中构建"二元表示体系":横轴仍对应实数(正实数居右、负实数居左),而纵轴则专门对应虚数(正虚数居上、负虚数居下),复数的雏形"实数+虚数"组合,便可对应平面内"横向位移+纵向位移"的合成结果,即坐标系中的一个点。为了让这一表示更具说服力,沃利斯还设计了具体的几何构造方法:对于复数对应的"实数+虚数"形式,他以实部绝对值和虚部绝对值为直角边作直角三角形,将斜边长度定义为该复数的"模长雏形",并通过几何证明指出,这一斜边长度与实数的绝对值具有相似的运算性质(如表征"大小"的量化功能)。不过,沃利斯的研究存在明显局限:他始终未将"实数+虚数"的组合视为独立的、不可分割的"数",仍将其看作两个独立部分的"拼接",也未基于这一几何表示推导复数四则运算的几何法则,再加上当时学界对虚数的质疑根深蒂固,其观点在当时未引起广泛关注,仅作为小众理论被记载于文献中。
进入19世纪初,瑞士数学家阿尔冈(Jean-Robert Argand)的研究实现了复数几何表示的关键突破。阿尔冈并非职业数学家,而是一位自学成才的巴黎簿记员,因长期处理商业数据中的线性运算问题,对"数的表示与运算的直观性"产生浓厚兴趣。1806年,他自费出版了一本匿名小册子《试论虚数的几何表示》(Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques),系统提出了与现代复平面几乎一致的几何表示体系。与沃利斯不同,阿尔冈首次明确将复数 z = a + b i z = a + b i z=a+bi定义为平面内的"独立点" ( a , b ) (a, b) (a,b),同时创新性地将其与"从原点指向该点的向量"建立一一对应关系------这一向量视角的引入,成为复数运算几何化的核心突破口。基于这一定义,阿尔冈进一步推导了完整的复数运算几何法则:加法运算对应向量的平行四边形法则(两个复数相加,即对应向量首尾相接或共起点合成新向量);乘法运算则拆解为"模长缩放"与"方向旋转"两个步骤,即两个复数相乘,其结果的模长等于两个复数模长的乘积,结果的方向(辐角)等于两个复数辐角的和。为了验证这一法则的合理性,阿尔冈还以具体复数运算为例进行验证,如 ( 1 + i ) ( 1 − i ) = 2 (1 + i)(1 - i) = 2 (1+i)(1−i)=2,对应几何意义为"模长 2 \sqrt{2} 2 、辐角45°的向量,与模长 2 \sqrt{2} 2 、辐角-45°的向量相乘,得到模长2、辐角0°的向量(即实数2)",与代数运算结果完全一致。遗憾的是,由于阿尔冈并非学界主流人物,且小册子匿名出版、发行量极小,其成果最初仅在小范围传播;直到1813年,法国数学家勒让德偶然发现该小册子并公开推荐,阿尔冈的研究才逐渐被学界知晓,但此时高斯的复平面理论已在逐步成型,其影响力最终未能超越高斯。
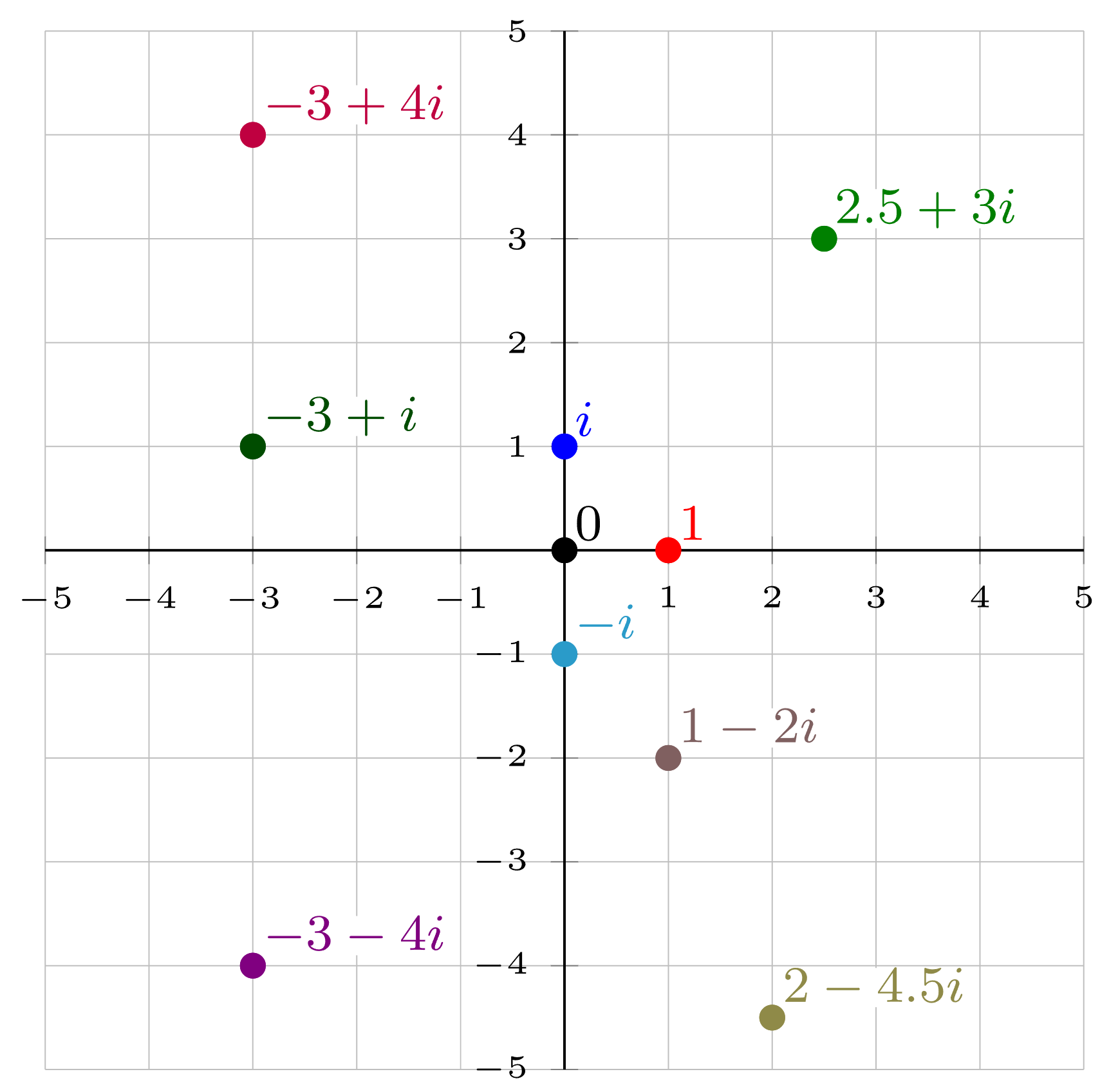
几乎与阿尔冈同时,挪威数学家韦塞尔(Caspar Wessel)从"向量分析"视角独立提出了复数的几何表示体系,且其理论严谨性与完整性毫不逊色。韦塞尔的本职工作是测量工程师,长期参与丹麦、挪威的地图测绘项目,在处理"平面内多方向位移的合成"问题时,深刻意识到需要一种能同时表征"大小"与"方向"的数学工具,这成为他探索复数几何意义的直接动力。1797年,韦塞尔向丹麦皇家科学院提交了论文《关于方向的分析表示》(Om directionens analytiske repræsentation),首次将复数定义为"具有大小和方向的有向线段"(即向量),并明确规定:实轴为水平向右的基准轴,实轴上的单位有向线段对应实数1;虚轴为垂直向上的轴,虚轴上的单位有向线段对应虚数单位 i i i。与阿尔冈相比,韦塞尔的研究更侧重于"运算的系统性":他不仅定义了复数的加法、乘法运算的几何法则,还进一步拓展到减法、除法运算,明确提出"复数减法对应向量的反向合成""复数除法对应模长相除、辐角相减";更重要的是,他首次引入了"辐角"的严格定义,将复数对应向量与实轴正方向的夹角(范围为-π到π)作为复数的核心属性,并用三角函数明确了复数实部、虚部与模长、辐角的关系(即 a = ∣ z ∣ c o s θ a = |z|cos\theta a=∣z∣cosθ, b = ∣ z ∣ s i n θ b = |z|sin\theta b=∣z∣sinθ),这一关系成为后续复数极坐标形式的核心基础。然而,韦塞尔的论文以丹麦语撰写,且发表于丹麦皇家科学院的内部期刊,当时欧洲主流数学界(以德语、法语、英语为主要交流语言)几乎无人知晓;直到1895年,该论文被译成法语重新发表,才被学界认可其价值,但此时复平面理论早已由高斯确立并普及,韦塞尔的贡献因此被长期埋没,仅作为"复数几何表示的独立探索者"被载入数学史。
1799年,高斯(Carl Friedrich Gauss)在首次证明"代数基本定理"(任何n次多项式方程在复数域内必有n个根,重根按重数计算)时,首次系统且严谨地整合了前人的探索成果,提出了"复平面"的完整理论框架。与沃利斯、阿尔冈、韦塞尔不同,高斯的核心优势在于"将几何表示与代数严谨性、分析应用深度融合":他不仅明确将复数 z = a + b i z = a + b i z=a+bi 与平面直角坐标系中的点 ( a , b ) (a, b) (a,b) 一一对应,将横坐标定义为实轴(Re轴)、纵坐标定义为虚轴(Im轴),正式命名这一平面为"复平面"(又称高斯平面);更重要的是,他将这一几何表示作为证明代数基本定理的核心工具------通过复平面上的点的运动轨迹,证明了多项式函数在复平面内必然存在零点,从而为复数的"合法性"提供了最坚实的理论支撑。高斯的研究并非停留在"定义与表示"层面,他还基于复平面完善了复数的运算逻辑:对于复数乘法,他从"代数基本定理的几何意义"出发,严格证明了"模长相乘、辐角相加"的合理性,指出这一运算规则与多项式因式分解的几何意义完全一致;对于复数的模长与辐角,他给出了严格的数学定义(区别于韦塞尔的"工程化定义"),将模长定义为"点到原点的距离",辐角定义为"向量与实轴正方向的最小正角",并明确了辐角的多值性与主值范围(0到2π),为后续复变函数的研究奠定了基础。此外,高斯还首次将复平面理论应用于实际科学问题,在天体力学研究中,他利用复数的几何表示简化了行星轨道的计算,证明了复平面理论的实用价值------这也是学界最终接受复数的关键原因之一。
复数的几何表示彻底改变了人们的认知:复数不再是"想象中的数",而是复平面上的一个点(或从原点指向该点的向量)。这一突破让复数获得"实体"意义,也为后续复指数、欧拉公式的发展奠定了几何基础。值得注意的是,高斯在后续研究中持续完善复平面理论,他还引入了"复数球面"(黎曼球面的雏形)概念,将复平面上的点与球面点一一对应,解决了无穷远点的几何表示问题,进一步拓展了复数几何意义的边界。
基于复平面,高斯系统定义了复数的模长与辐角,完善了前人未厘清的核心概念:
借助模长与辐角,复数还可表示为"极坐标形式": z = ∣ z ∣ ( c o s θ + i s i n θ ) z = |z|(cos\theta + i sin\theta) z=∣z∣(cosθ+isinθ)。这种形式将复数与三角函数关联起来,既延续了棣莫弗公式中复数幂运算与三角运算的联系,也为复指数的引入埋下了伏笔。需要强调的是,极坐标形式的普及,离不开高斯对复平面理论的系统推广------他在1811年给贝塞尔的信件中,明确使用极坐标形式描述复数,并将其应用于天体力学、电磁学等领域的计算,证明了该形式的实用性。
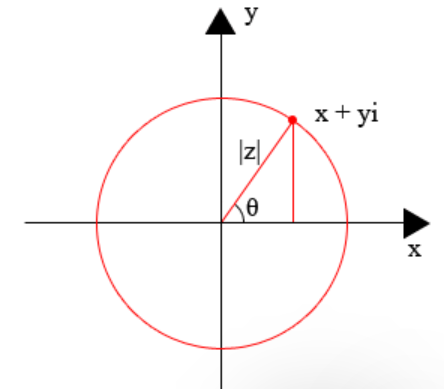
- 模长(绝对值):复数 z = a + b i z = a + b i z=a+bi 对应的向量长度,记为 ∣ z ∣ |z| ∣z∣,即 ∣ z ∣ = a 2 + b 2 |z| = \sqrt{a^2 + b^2} ∣z∣=a2+b2 (本质是该点到原点的距离)。这一定义整合了沃利斯的斜边长度思想,成为复数几何意义的核心量化指标;
- 辐角:复数对应的向量与实轴正方向的夹角,记为 a r g ( z ) arg(z) arg(z),满足 c o s θ = a ∣ z ∣ cos\theta = \frac{a}{|z|} cosθ=∣z∣a, s i n θ = b ∣ z ∣ sin\theta = \frac{b}{|z|} sinθ=∣z∣b( θ \theta θ 即为辐角)。辐角的明确的定义,让阿尔冈、韦塞尔提出的"旋转运算"有了精准的数学表达。
1831年,高斯在《关于复数的几何表示》(Theoria Residuorum Biquadraticorum Commentatio Secunda)一文中,系统总结了复数的几何意义与运算性质,正式将沃利斯的"模长雏形"、阿尔冈的"向量表示"、韦塞尔的"辐角定义"整合为统一的理论体系,彻底确立了复数的数学地位。高斯的工作之所以能打破学界对复数的质疑,关键在于三点:一是理论的系统性,他将几何表示、代数运算、分析应用融为一体,形成了"定义-性质-证明-应用"的完整逻辑链,让复数不再是孤立的"符号"或"工具",而是具备严谨理论基础的数学概念;二是证明的严谨性,通过代数基本定理的严格证明,验证了复数域的完备性(即任何代数方程在复数域内都有完整解),填补了实数域的理论空白;三是应用的广泛性,他将复数应用于天体力学、电磁学、数论等多个领域,如在数论中利用复平面研究二次型的分解问题,在电磁学中用复数表示电场强度的大小与方向,充分展现了复数的理论价值与实用价值。从此,复数成为数学领域不可或缺的重要概念,其几何意义的深入挖掘,也推动了复变函数、拓扑学等新兴学科的发展,应用逐渐延伸到物理、工程等多个领域。
借助模长与辐角,复数还可表示为"极坐标形式": z = ∣ z ∣ ( c o s θ + i s i n θ ) z = |z|(cos\theta + i sin\theta) z=∣z∣(cosθ+isinθ)。这种形式将复数与三角函数关联起来,不仅简化了复数的乘方、开方运算,更让复数的几何意义得以量化表达------模长表征"向量的长度",辐角表征"向量的方向",为复数在需要"同时描述大小与方向"的领域应用提供了便利。而复数几何意义的实际价值,也在后续的科学与工程实践中得到充分体现。
3、指数的跨越:复指数函数的构建(18世纪:欧拉的大胆推广)
复指数与我们后面要介绍的欧拉公式密不可分,两部分都是由欧拉进行了完善的分析和研究,但是由于内容太多分为了两部分。
在复数确立之前,指数函数 e x e^x ex(其中 e e e 是自然常数,约等于2.71828)的定义域仅限于实数。人们已经掌握了实数指数函数的核心性质:
-
指数运算法则: e x ⋅ e y = e x + y e^x \cdot e^y = e^{x + y} ex⋅ey=ex+y, ( e x ) y = e x y (e^x)^y = e^{xy} (ex)y=exy
-
幂级数展开式: e x = ∑ n = 0 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots ex=∑n=0∞n!xn=1+x+2!x2+3!x3+⋯(收敛域为全体实数)。
这一展开式的形成与泰勒(Brook Taylor)的工作密切相关,但并非由泰勒单独完成。1715年,泰勒在著作《正和反的增量方法》中提出了函数幂级数展开的通用理论------泰勒定理,指出"足够光滑的函数可以表示为以函数各阶导数为系数的幂级数形式",即任意函数 f ( x ) f(x) f(x) 在 x = 0 x=0 x=0 处的泰勒级数为 f ( x ) = ∑ n = 0 ∞ f ( n ) ( 0 ) n ! x n f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^n f(x)=∑n=0∞n!f(n)(0)xn(也称为麦克劳林级数,由麦克劳林后续简化完善)。泰勒定理为指数函数的幂级数展开提供了核心方法论基础,但泰勒本人并未明确推导指数函数的具体展开式。事实上,在泰勒之前,牛顿(Isaac Newton)已在17世纪末通过无穷级数的运算,初步得到了指数函数展开的近似形式,但未形成严格的理论框架;直到18世纪,欧拉(Leonhard Euler)在1748年出版的《无穷分析引论》中,基于泰勒定理,结合自然常数 e e e 的定义( e = lim n → ∞ ( 1 + 1 n ) n e = \lim_{n \to \infty}(1 + \frac{1}{n})^n e=limn→∞(1+n1)n),首次严谨推导并明确给出了 e x e^x ex 的幂级数展开式,同时验证了该级数在全体实数域内的收敛性,最终确立了这一展开式的标准形式。
瑞士数学家欧拉是推动指数函数域拓展的核心人物,其契机主要源于两方面:一是数学理论内在统一性的追求,欧拉始终致力于构建连贯的数学体系,他认为指数运算作为基本运算,理应像加减乘除一样适用于已确立的复数域,以填补"复数运算体系的最后一块空白";二是解决实际物理问题的需求,18世纪波动现象(如弦振动、声波传播)的研究需要求解复杂的微分方程(如弦振动方程 u t t = a 2 u x x u_{tt} = a^2 u_{xx} utt=a2uxx),传统实数域的指数函数难以简洁描述波动的相位变化,欧拉预判若能将指数函数推广到复数域,有望为这类物理问题提供更高效的求解工具。基于此,欧拉率先提出疑问:能否将指数函数的定义域推广到复数域,构建一个"复指数函数" e z e^z ez(其中 z = x + y i z = x + y i z=x+yi为复数)?
要构建复指数函数,必须满足两个核心条件:一是继承实数指数函数的基本性质(尤其是 e z 1 ⋅ e z 2 = e z 1 + z 2 e^{z_1} \cdot e^{z_2} = e^{z_1 + z_2} ez1⋅ez2=ez1+z2);二是当复数的虚部为0时(即 z = x z = x z=x),复指数函数应退化为实数指数函数 e x e^x ex。欧拉的核心思路是:既然实数指数函数可以用幂级数表示,而幂级数的运算规则(加法、乘法、逐项求导等)在复数域内依然成立,那么可以直接将实数指数函数的幂级数展开式推广到复数域,以此定义复指数函数。1748年,欧拉在《无穷分析引论》中,正式定义了复指数函数:对于任意复数 z = x + y i z = x + y i z=x+yi,复指数函数 e z e^z ez 的幂级数展开式为:
e z = ∑ n = 0 ∞ z n n ! = 1 + z + z 2 2 ! + z 3 3 ! + ⋯ e^z = \sum_{n=0}^{\infty} \frac{z^n}{n!} = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \cdots ez=n=0∑∞n!zn=1+z+2!z2+3!z3+⋯
第一重验证:兼容性验证(满足退化一致性)。当复数z的虚部y=0时,z=x为实数,此时复指数函数的幂级数展开式即为实数指数函数eˣ的幂级数展开式,即 e x = ∑ n = 0 ∞ x n n ! e^x=\sum_{n=0}^\infty{\frac{x^n}{n!}} ex=∑n=0∞n!xn,完美退化为已知的实数指数函数,验证了定义的"兼容性"。
第二重验证:运算性质验证(满足运算继承性)。为证明定义满足指数加法定理 e z 1 ⋅ e z 2 = e z 1 + z 2 e^{z_1} \cdot e^{z_2} = e^{z_1 + z_2} ez1⋅ez2=ez1+z2(其中 z 1 z_1 z1、 z 2 z_2 z2为任意复数),欧拉采用了幂级数的柯西乘积法则进行严谨证明:设 z 1 = a + b i z_1 = a + b i z1=a+bi, z 2 = c + d i z_2 = c + d i z2=c+di,将 e z 1 e^{z_1} ez1与 e z 2 e^{z_2} ez2的幂级数展开式相乘,得到双重求和形式 ∑ n = 0 ∞ z 1 n n ! ⋅ ∑ m = 0 ∞ z 2 m m ! \sum_{n=0}^{\infty} \frac{z_1^n}{n!} \cdot \sum_{m=0}^{\infty} \frac{z_2^m}{m!} ∑n=0∞n!z1n⋅∑m=0∞m!z2m。通过合并同类项(令 k = n + m k = n + m k=n+m),可将双重求和转化为单求和形式 ∑ k = 0 ∞ [ ∑ n = 0 k z 1 n z 2 k − n n ! ( k − n ) ! ] \sum_{k=0}^{\infty} \left[ \sum_{n=0}^k \frac{z_1^n z_2^{k - n}}{n! (k - n)!} \right] ∑k=0∞[∑n=0kn!(k−n)!z1nz2k−n]。根据二项式定理,内层求和项 ∑ n = 0 k z 1 n z 2 k − n n ! ( k − n ) ! = ( z 1 + z 2 ) k k ! \sum_{n=0}^k \frac{z_1^n z_2^{k - n}}{n! (k - n)!} = \frac{(z_1 + z_2)^k}{k!} ∑n=0kn!(k−n)!z1nz2k−n=k!(z1+z2)k,因此最终乘积结果为 ∑ k = 0 ∞ ( z 1 + z 2 ) k k ! = e z 1 + z 2 \sum_{k=0}^{\infty} \frac{(z_1 + z_2)^k}{k!} = e^{z_1 + z_2} ∑k=0∞k!(z1+z2)k=ez1+z2,成功验证了指数加法定理在复数域内依然成立。
第三重验证:收敛性验证(保证定义域完整性)。欧拉通过比值判别法证明,复指数函数的幂级数展开式收敛半径为无穷大。对于任意给定的复数 z = x + y i z=x+yi z=x+yi,计算幂级数的相邻两项比值的模长 ∣ a n + 1 / a n ∣ = ∣ z n + 1 ( n + 1 ) ! ∣ ⋅ ∣ n ! z n ∣ = ∣ z ∣ n + 1 |a_{n+1}/a_n| = \left| \frac{z^{n+1}}{(n+1)!} \right| \cdot \left| \frac{n!}{z^n} \right| = \frac{|z|}{n+1} ∣an+1/an∣= (n+1)!zn+1 ⋅ znn! =n+1∣z∣,当 n → ∞ n \to \infty n→∞时,该比值的极限为0,小于1,因此幂级数对所有复数 z z z均收敛。这意味着复指数函数的定义域为全体复数,不存在"发散的漏洞",保证了定义的"完整性"。
欧拉进一步将 z = x + y i z = x + y i z=x+yi 代入展开式,拆分实部与虚部:
e x + y i = ∑ n = 0 ∞ ( x + y i ) n n ! = ∑ n = 0 ∞ 1 n ! ∑ k = 0 n C n k x n − k ( y i ) k = ∑ n = 0 ∞ 1 n ! ( ∑ k = 0 ⌊ n / 2 ⌋ ( − 1 ) k n ! ( n − 2 k ) ! ( 2 k ) ! x n − 2 k y 2 k + i ∑ k = 0 ⌊ ( n − 1 ) / 2 ⌋ ( − 1 ) k n ! ( n − 2 k − 1 ) ! ( 2 k + 1 ) ! x n − 2 k − 1 y 2 k + 1 ) \begin{align} e^{x + y i} &= \sum_{n=0}^{\infty} \frac{(x + y i)^n}{n!} \\ &= \sum_{n=0}^{\infty} \frac{1}{n!} \sum_{k=0}^n C_n^k x^{n - k} (y i)^k \\ &= \sum_{n=0}^{\infty} \frac{1}{n!} \left( \sum_{k=0}^{\lfloor n/2 \rfloor} (-1)^k \frac{n!}{(n - 2k)! (2k)!} x^{n - 2k} y^{2k} + i \sum_{k=0}^{\lfloor (n - 1)/2 \rfloor} (-1)^k \frac{n!}{(n - 2k - 1)! (2k + 1)!} x^{n - 2k - 1} y^{2k + 1} \right) \end{align} ex+yi=n=0∑∞n!(x+yi)n=n=0∑∞n!1k=0∑nCnkxn−k(yi)k=n=0∑∞n!1 k=0∑⌊n/2⌋(−1)k(n−2k)!(2k)!n!xn−2ky2k+ik=0∑⌊(n−1)/2⌋(−1)k(n−2k−1)!(2k+1)!n!xn−2k−1y2k+1
交换求和顺序后,可拆分为两个独立的幂级数:
e x + y i = ( ∑ k = 0 ∞ ( − 1 ) k y 2 k ( 2 k ) ! ∑ n = 2 k ∞ x n − 2 k ( n − 2 k ) ! ) + i ( ∑ k = 0 ∞ ( − 1 ) k y 2 k + 1 ( 2 k + 1 ) ! ∑ n = 2 k + 1 ∞ x n − 2 k − 1 ( n − 2 k − 1 ) ! ) e^{x + y i} = \left( \sum_{k=0}^{\infty} \frac{(-1)^k y^{2k}}{(2k)!} \sum_{n=2k}^{\infty} \frac{x^{n - 2k}}{(n - 2k)!} \right) + i \left( \sum_{k=0}^{\infty} \frac{(-1)^k y^{2k + 1}}{(2k + 1)!} \sum_{n=2k + 1}^{\infty} \frac{x^{n - 2k - 1}}{(n - 2k - 1)!} \right) ex+yi=(k=0∑∞(2k)!(−1)ky2kn=2k∑∞(n−2k)!xn−2k)+i(k=0∑∞(2k+1)!(−1)ky2k+1n=2k+1∑∞(n−2k−1)!xn−2k−1)
注意到内层的求和正是实数指数函数 e x e^x ex 的幂级数展开式,因此:
e x + y i = e x ∑ k = 0 ∞ ( − 1 ) k y 2 k ( 2 k ) ! + i e x ∑ k = 0 ∞ ( − 1 ) k y 2 k + 1 ( 2 k + 1 ) ! e^{x + y i} = e^x \sum_{k=0}^{\infty} \frac{(-1)^k y^{2k}}{(2k)!} + i e^x \sum_{k=0}^{\infty} \frac{(-1)^k y^{2k + 1}}{(2k + 1)!} ex+yi=exk=0∑∞(2k)!(−1)ky2k+iexk=0∑∞(2k+1)!(−1)ky2k+1
而这两个求和式,恰好是余弦函数和正弦函数的幂级数展开式:
c o s y = ∑ k = 0 ∞ ( − 1 ) k y 2 k ( 2 k ) ! , s i n y = ∑ k = 0 ∞ ( − 1 ) k y 2 k + 1 ( 2 k + 1 ) ! cos y = \sum_{k=0}^{\infty} \frac{(-1)^k y^{2k}}{(2k)!}, \quad sin y = \sum_{k=0}^{\infty} \frac{(-1)^k y^{2k + 1}}{(2k + 1)!} cosy=k=0∑∞(2k)!(−1)ky2k,siny=k=0∑∞(2k+1)!(−1)ky2k+1
由此,欧拉得到了复指数函数的另一种表达形式------"指数形式"与"三角形式"的转换公式:
e x + y i = e x ( c o s y + i s i n y ) e^{x + y i} = e^x (cos y + i sin y) ex+yi=ex(cosy+isiny)
这一公式将复指数函数与三角函数紧密关联,是后续欧拉公式推导的关键铺垫。
4、数学的"最美公式":欧拉公式的推导与意义(1748年)
4.1 欧拉公式的直接推导
在复指数函数的表达式 e x + y i = e x ( c o s y + i s i n y ) e^{x + y i} = e^x (cos y + i sin y) ex+yi=ex(cosy+isiny) 中,令实部 x = 0 x = 0 x=0,则复数 z = 0 + y i = y i z = 0 + y i = y i z=0+yi=yi(纯虚数),代入后即可得到欧拉公式。值得注意的是,欧拉公式的诞生并非一蹴而就,其前期既有多位学者的研究成果奠定基础,也与二阶微分方程的求解探索密切相关。从求解需求来看,18世纪,物理学对波动现象(如弦振动、声波传播)的研究日益深入,描述这类现象的核心方程是二阶线性偏微分方程(如弦振动方程 u t t = a 2 u x x u_{tt} = a^2 u_{xx} utt=a2uxx)。当时,数学家采用传统实数函数解法时存在局限性,难以简洁描述波动的相位变化与传播规律。欧拉在研究弦振动方程通解时发现,引入复指数函数 e i ( k x − ω t ) e^{i(kx - \omega t)} ei(kx−ωt)(其中k为波数、 ω \omega ω 为角频率)后,借助欧拉公式可将其转化为 c o s ( k x − ω t ) + i s i n ( k x − ω t ) cos(kx - \omega t) + i sin(kx - \omega t) cos(kx−ωt)+isin(kx−ωt),而余弦与正弦函数正是描述简谐振动的基础函数。通过这一转化,不仅能将复杂的偏微分方程求解转化为简便的代数运算,还能统一描述波动的振幅与相位信息,大幅简化求解过程。这一应用场景不仅验证了复指数函数与欧拉公式的合理性,还让它们从纯粹的数学理论走向实际物理应用,进一步巩固了其在数学与物理领域的核心地位。这种偏微分方程可以统一为 y ′ ′ + y = 0 y'' + y = 0 y′′+y=0 这类的形式,欧拉在求解过程中发现,这个方程存在两类看似完全不同的解:一类是三角函数解 y = A c o s x + B s i n x y = A cos x + B sin x y=Acosx+Bsinx(其中A、B为任意常数),这是基于几何直观和三角函数性质得出的;另一类是指数函数形式的解,但这类指数函数需突破实数域限制------假设解为 y = e k x y = e^{kx} y=ekx(k为常数),代入方程 y ′ ′ + y = 0 y'' + y = 0 y′′+y=0 后,可得到特征方程 k 2 + 1 = 0 k^2 + 1 = 0 k2+1=0,其解为 k = ± i k = \pm i k=±i(虚数单位),因此方程的指数形式解为 y = e i x y = e^{i x} y=eix 和 y = e − i x y = e^{-i x} y=e−ix。
这一发现让欧拉敏锐意识到:同一个微分方程的解,形式上却分属指数函数和三角函数两类,背后必然存在深层次的内在联系,而非偶然巧合。结合当时已有的研究基础,这一认知进一步推动了他的探索。其中最具代表性的是瑞士数学家雅各布·伯努利(Jakob Bernoulli)与法国数学家棣莫弗(Abraham de Moivre):雅各布·伯努利在1702年研究复数幂运算时,发现了复数与三角函数的潜在关联,尝试用指数运算表示复数乘方,虽未得出明确公式,却开启了"指数与三角关联"的研究方向;棣莫弗在1730年的《分析杂论》中提出"棣莫弗公式"------ ( c o s θ + i s i n θ ) n = c o s n θ + i s i n n θ (cos\theta + i sin\theta)^n = cos n\theta + i sin n\theta (cosθ+isinθ)n=cosnθ+isinnθ(n为整数),直接搭建了复数幂运算与三角函数的桥梁,且当n为有理数时公式依然成立,已蕴含"复指数与三角函数对应"的核心思想。欧拉正是在求解 y ′ ′ + y = 0 y'' + y = 0 y′′+y=0 得到"指数解与三角解共存"的启发下,结合棣莫弗公式与幂级数理论,将指数函数定义域拓展到复数域,最终推导出形式更简洁、适用范围更广泛的欧拉公式,完成了对前期研究成果的升华与统一,也彻底厘清了两类解的内在等价性。
e i y = c o s y + i s i n y e^{i y} = cos y + i sin y eiy=cosy+isiny
这就是著名的"欧拉公式"(也称为欧拉方程)。当 y = π y = \pi y=π 时,欧拉公式变为:
e i π + 1 = 0 e^{i \pi} + 1 = 0 eiπ+1=0
这个公式被称为"上帝创造的公式",它将数学中最核心的五个常数------自然常数 e e e、虚数单位 i i i、圆周率 π \pi π、自然数单位 1 1 1、零 0 0 0 完美融合在一个等式中,展现了数学的极致和谐。
回顾欧拉公式的推导过程,其核心逻辑链是:
- 基于实数指数函数的幂级数展开式,推广得到复指数函数的幂级数定义;
- 将复指数函数的幂级数拆分为实部和虚部,发现其分别对应余弦函数和正弦函数的幂级数;
- 令实部为0,得到纯虚数的复指数表达式,即欧拉公式。
这一推导过程看似顺理成章,背后却蕴含着欧拉的大胆创新与多领域研究的融合:一方面,他从 y ′ ′ + y = 0 y'' + y = 0 y′′+y=0 的求解中洞察到指数与三角函数的深层关联,明确了探索方向;另一方面,他打破实数与复数、指数函数与三角函数的界限,借助幂级数工具将看似无关的数学概念统一起来。值得补充的是,欧拉公式的诞生也反过来完善了微分方程求解理论------通过欧拉公式可将 y ′ ′ + y = 0 y'' + y = 0 y′′+y=0 的复指数解转化为三角函数解,由此确立了二阶线性微分方程"特征根法"的通用性:无论特征根是实数还是虚数,都能通过统一方法得到方程通解,极大推动了微分方程理论的发展。
4.2 欧拉公式的几何意义
结合复数的极坐标形式,欧拉公式还具有深刻的几何意义。复平面上,纯虚数 e i y e^{i y} eiy 对应的点的极坐标为 ( ∣ e i y ∣ , y ) (|e^{i y}|, y) (∣eiy∣,y):
- 模长: ∣ e i y ∣ = c o s 2 y + s i n 2 y = 1 |e^{i y}| = \sqrt{cos^2 y + sin^2 y} = 1 ∣eiy∣=cos2y+sin2y =1,即该点位于复平面的单位圆上;
- 辐角: a r g ( e i y ) = y arg(e^{i y}) = y arg(eiy)=y,即该点与实轴正方向的夹角为 y y y(弧度制)。
因此,欧拉公式 e i y = c o s y + i s i n y e^{i y} = cos y + i sin y eiy=cosy+isiny 的几何意义是:复平面上,模长为1、辐角为 y y y 的单位复数,等价于以 e e e 为底、纯虚数 i y i y iy 为指数的复指数。
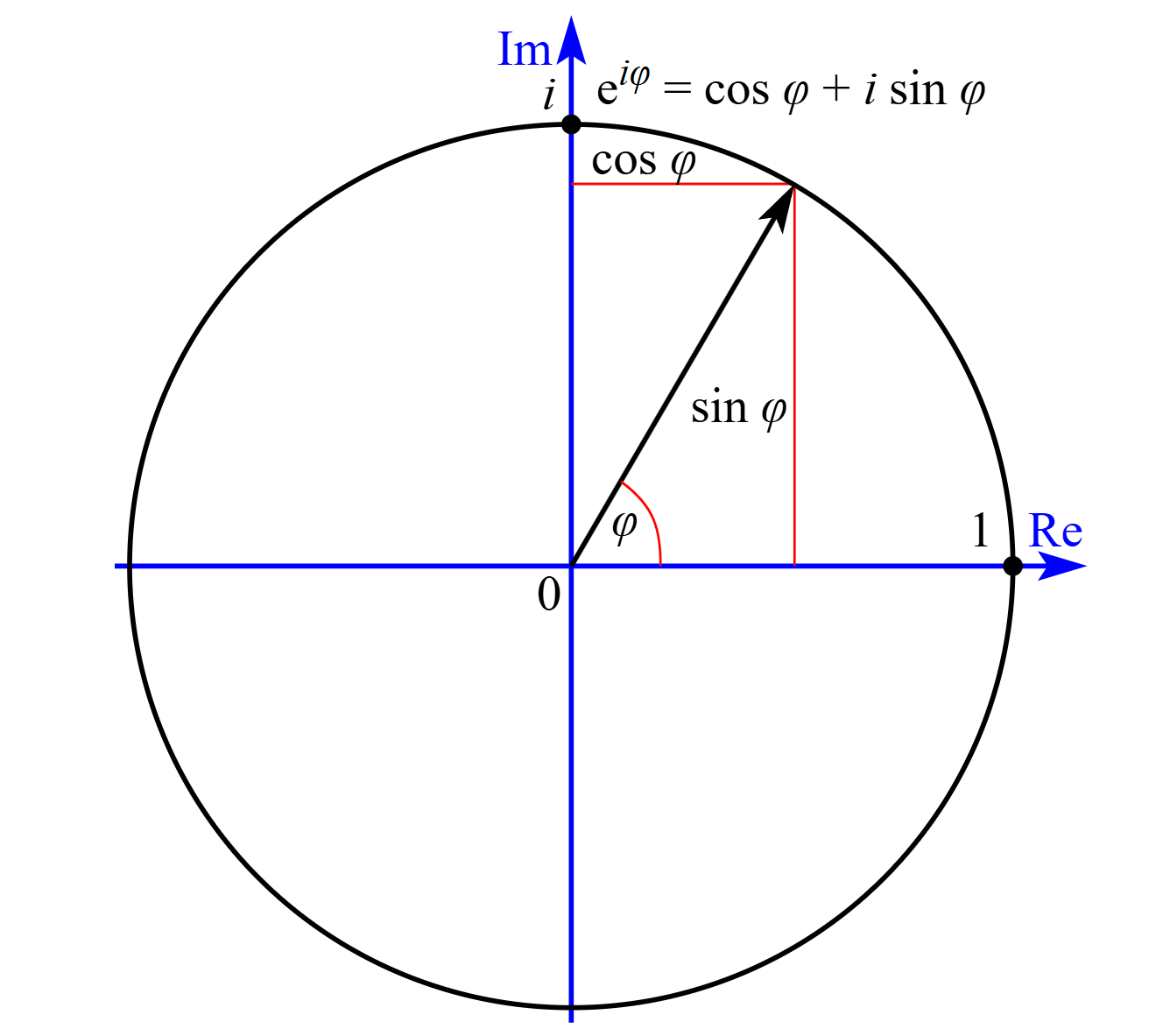
这一几何意义还可以解释复指数的"旋转"性质:当我们对一个复数 z z z 乘以 e i y e^{i y} eiy 时,相当于将 z z z 对应的向量在复平面上绕原点逆时针旋转 y y y 角度(模长保持不变)。例如,复数 1 1 1 乘以 e i π e^{i \pi} eiπ 后,得到 e i π = − 1 e^{i \pi} = -1 eiπ=−1,相当于将向量 1 1 1 旋转 π \pi π(180度),复数 1 1 1 乘以 e i π / 2 e^{i \pi/2} eiπ/2 后,得到 e i π / 2 = i e^{i \pi/2} = i eiπ/2=i,相当于将向量 1 1 1 旋转 π / 2 \pi/2 π/2,这与几何直观完全一致。
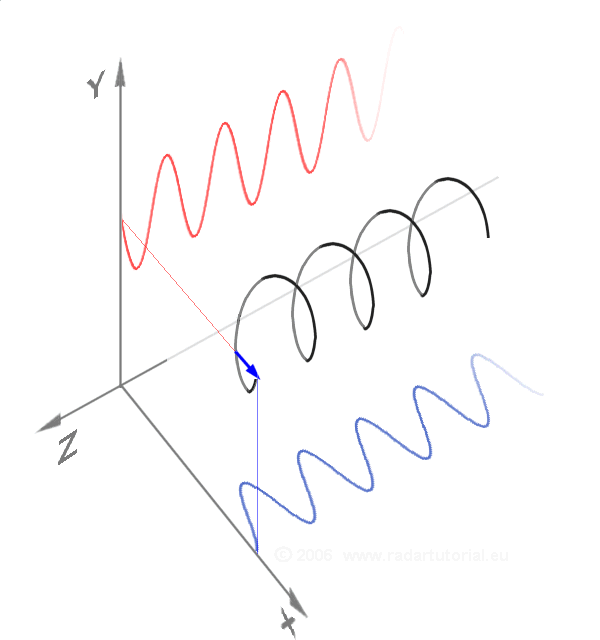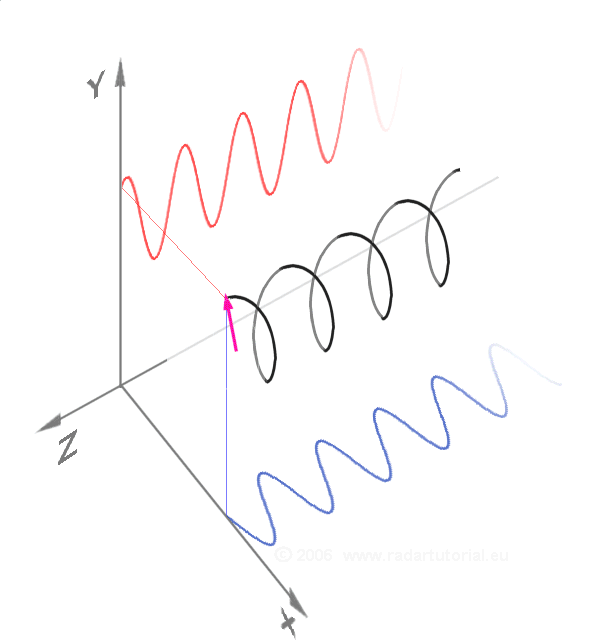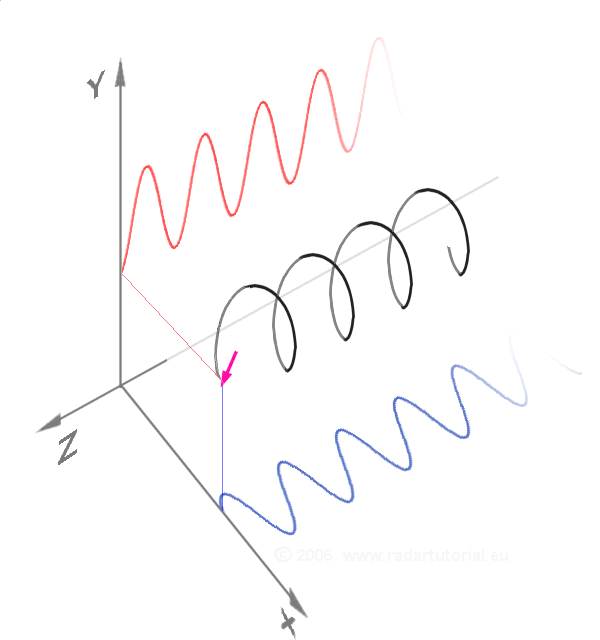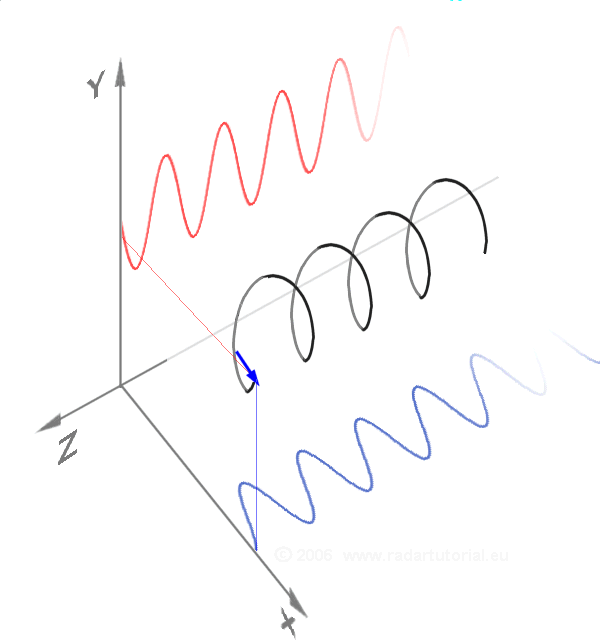
特别的,有些介绍文档中还提到了i的高次方,借助欧拉公式,也就更好理解,每次乘i,相当于逆时针旋转 p i / 2 pi/2 pi/2:

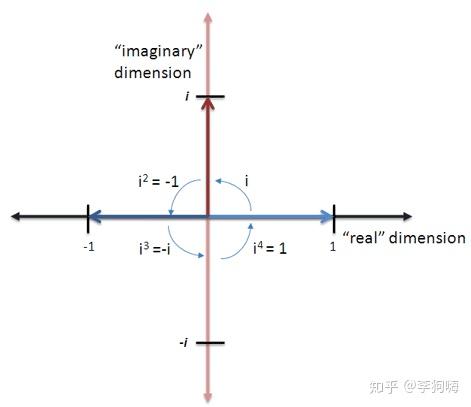
4.3 欧拉公式的历史意义
欧拉公式的诞生,不仅是复数理论发展的巅峰,也对整个数学乃至物理领域产生了深远影响:
- 统一了代数、几何与分析:欧拉公式将代数中的指数运算、几何中的旋转(单位圆)、分析中的三角函数与幂级数完美融合,构建了数学不同分支之间的桥梁;
- 推动了复数理论的完善:欧拉公式让复数的极坐标形式( z = ∣ z ∣ e i θ z = |z| e^{i \theta} z=∣z∣eiθ)成为可能,极大简化了复数的乘法、除法、乘方、开方运算(例如,两个复数相乘,只需将模长相乘、辐角相加);
- 奠定了近代物理的数学基础:在电磁学、量子力学、信号处理等领域,欧拉公式是描述波动、振动、相位变化的核心工具(例如,交流电的相位表示、量子力学中的波函数)。
5、总结:从"被迫妥协"到"主动构建"的数学思维跃迁
回顾虚数、复数、复指数与欧拉公式的发展历程,我们能清晰看到数学思维的演变轨迹:
16世纪,虚数因三次方程求解的"被迫需求"而诞生,此时的数学家们对其充满质疑,仅将其视为"工具";17世纪,笛卡尔确立了虚数与实数的命名,欧拉提出复数的代数形式,让复数逐渐成为独立的数学概念;18世纪,高斯的复平面赋予复数几何意义,彻底消除了人们对复数的质疑;随后,欧拉通过推广实数指数函数的幂级数,构建了复指数函数,并最终推导出欧拉公式,完成了从"虚数"到"复数"、从"代数"到"几何与分析"的全面统一。
高斯奠定了复数的基础后,黎曼(Bernhard Riemann)在19世纪末通过复变函数论进一步扩展了虚数的应用。他构建了黎曼面,使得多值复变函数得以完美地解析。黎曼认为,复数和虚数在描述连续现象和几何空间时具有独特的优势,广泛应用于积分、微分方程和物理学理论中。
进入20世纪,虚数成为现代数学、物理学和工程学不可或缺的工具。量子力学之父薛定谔(Erwin Schrödinger)在描述粒子的波动现象时使用了复数波函数,虚数在量子力学中用于描述粒子的状态和演化。保罗·狄拉克(Paul Dirac)进一步将虚数与电磁场、相对论结合,揭示了电子和正电子的存在。虚数在现代物理学中被视为真实物理现象的数学表现。
在工程领域,虚数被用于电路分析、信号处理和控制理论。例如,奈奎斯特(Harry Nyquist)和布德维奇(Ragazzini Bode)通过复数方法分析线性系统的稳定性,奠定了现代控制系统理论的基础。傅里叶变换和拉普拉斯变换则成为信号与图像处理的核心工具,虚数在现代通信技术中发挥了巨大作用。
参考文献:
1、虚数上位史
4、三次方程