简单多边形三角剖分---耳切法（含源码）

先看效果：

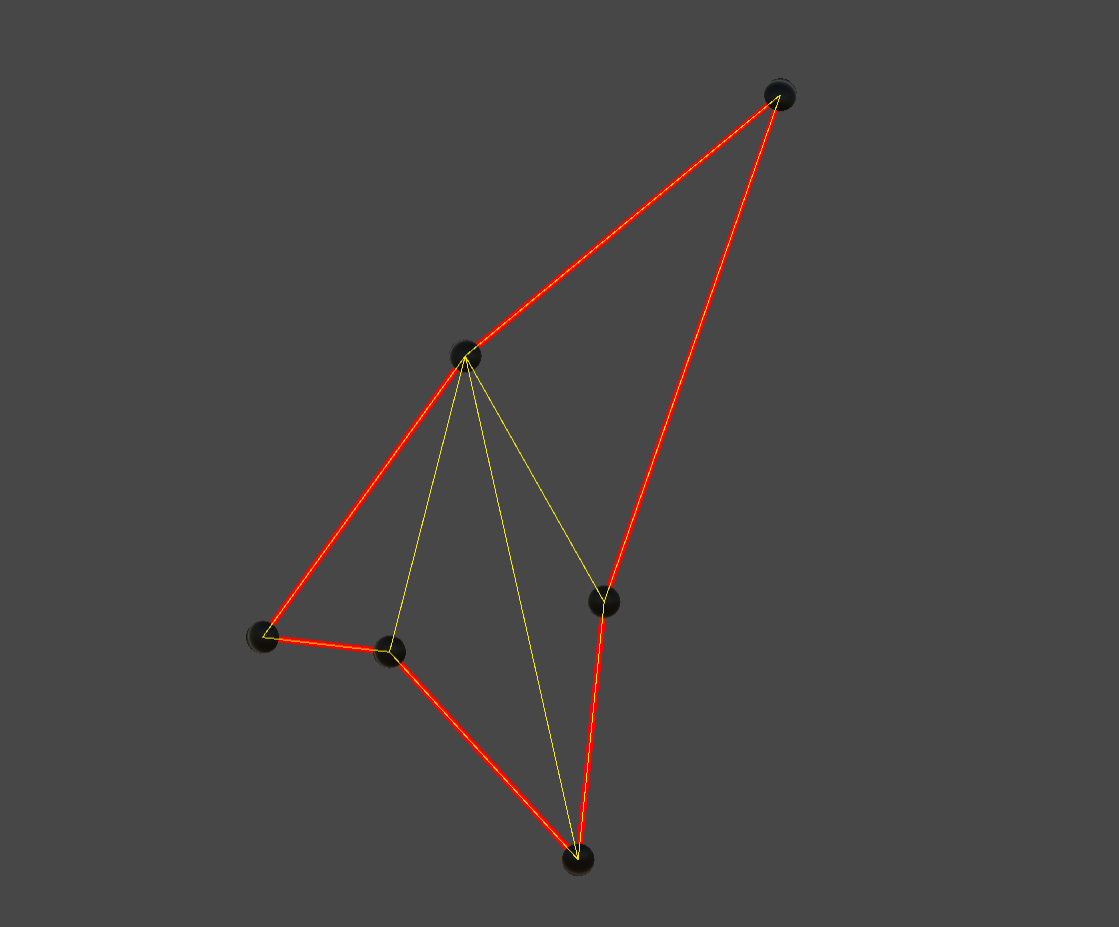
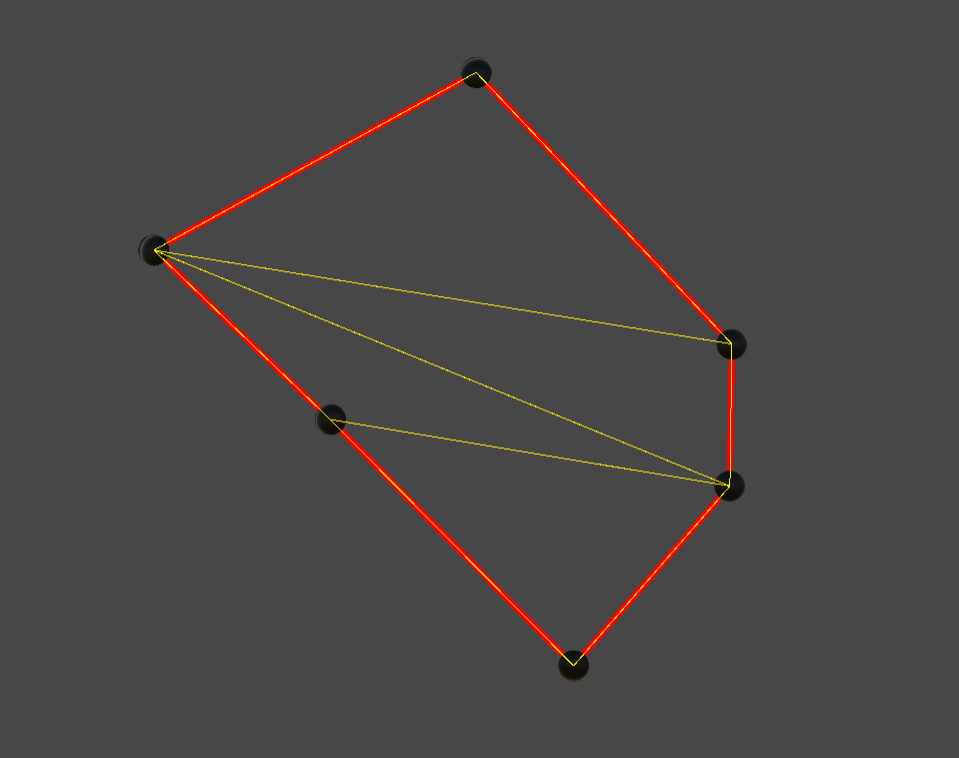
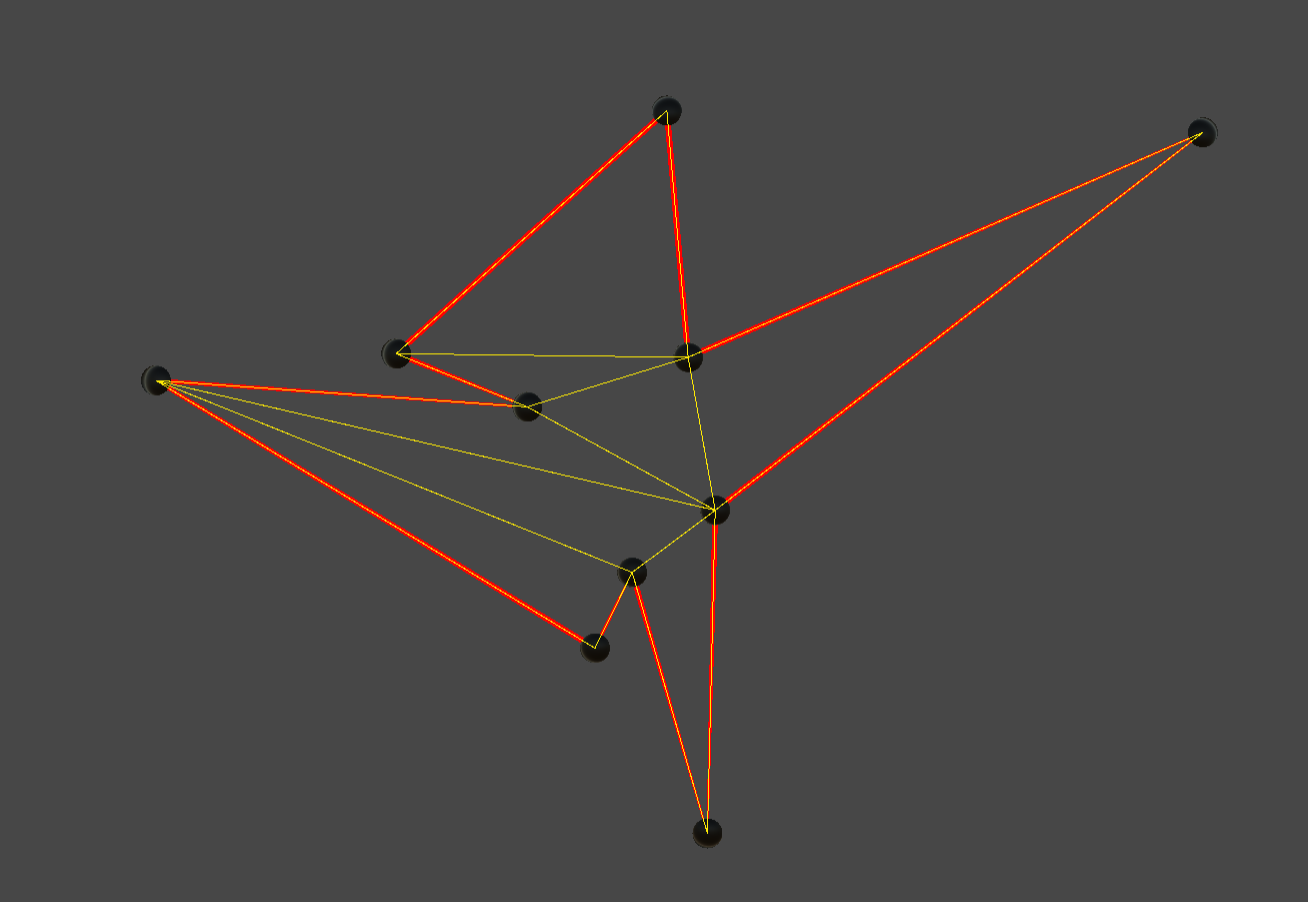
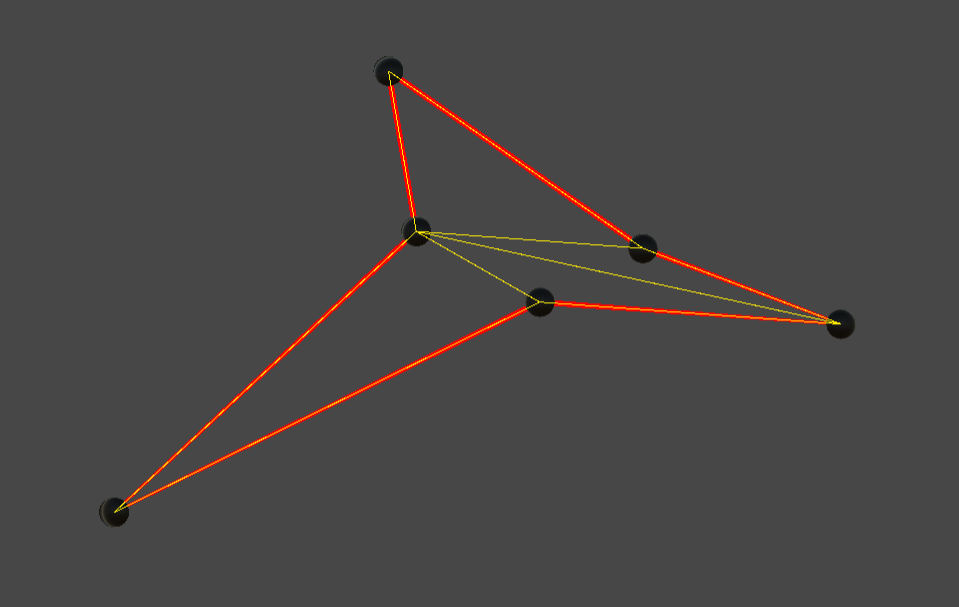
一、耳切法简单定义

简单多边形：由一系列顶点按顺序连接而成的封闭图形，其边除了在顶点处外，彼此不相交。
耳朵：
- 由三个连续顶点 V(i-1), V(i), V(i+1) 组成的三角形。
- 这个三角形必须是凸的（内角 < 180°）。
- 这个三角形的内部不能包含多边形的任何其他顶点。
- 顶点 V(i) 被称为耳尖（Ear Tip）。
三角剖分：将多边形分解为一系列互不重叠的三角形的集合，这些三角形的并集完全等于原始多边形。

二、耳切法流程

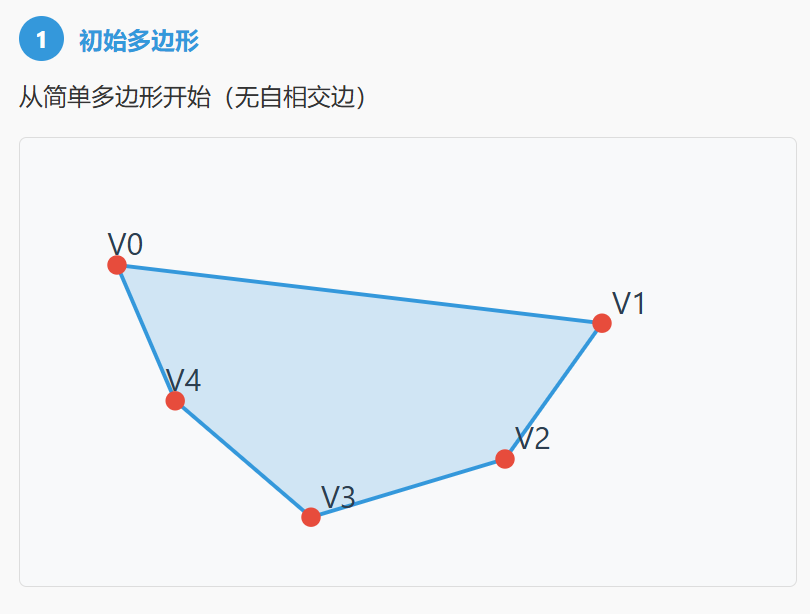
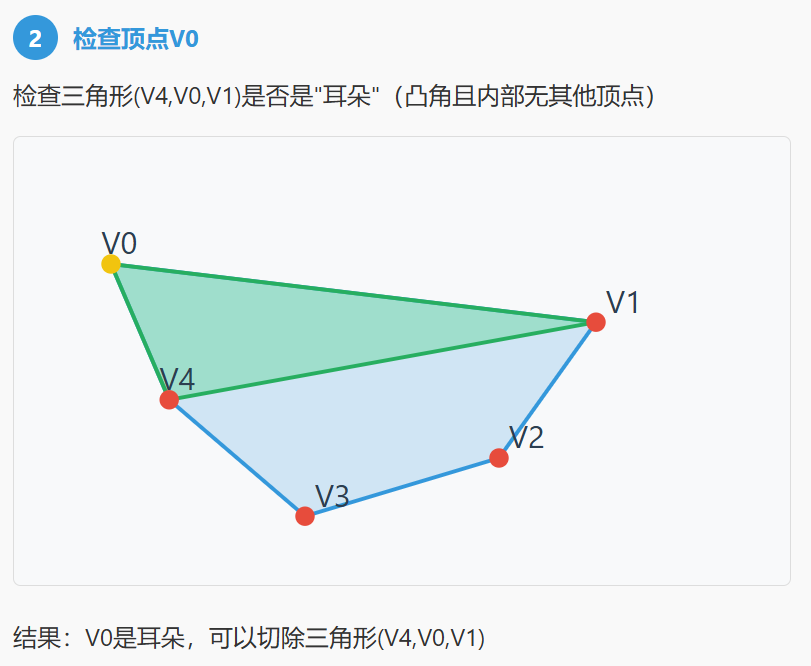
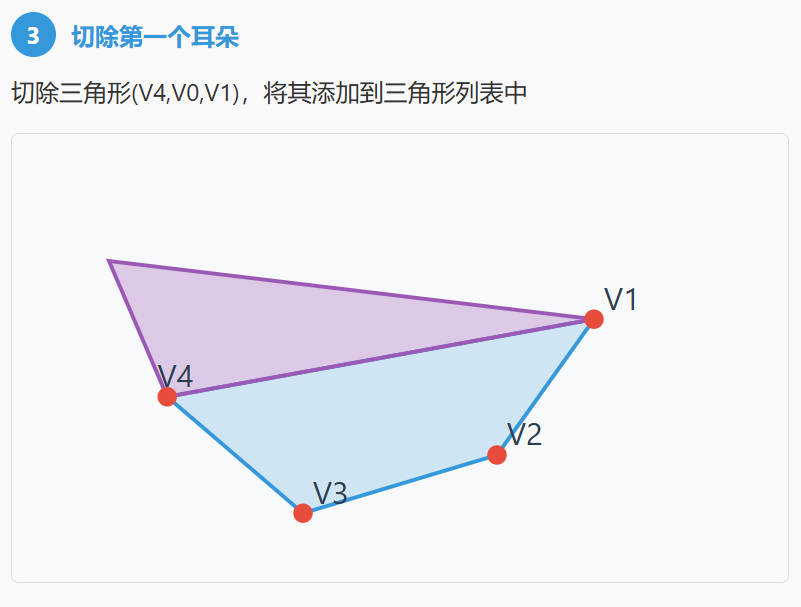
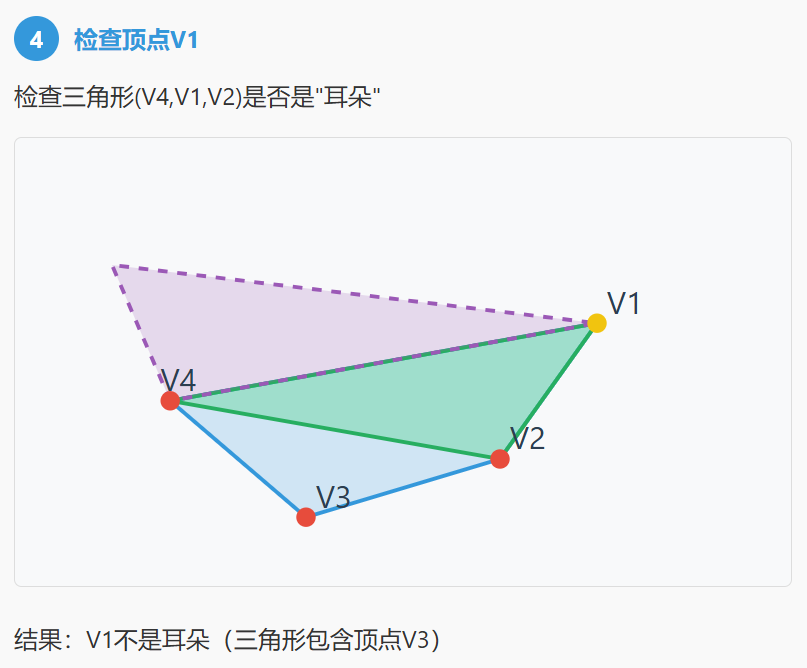
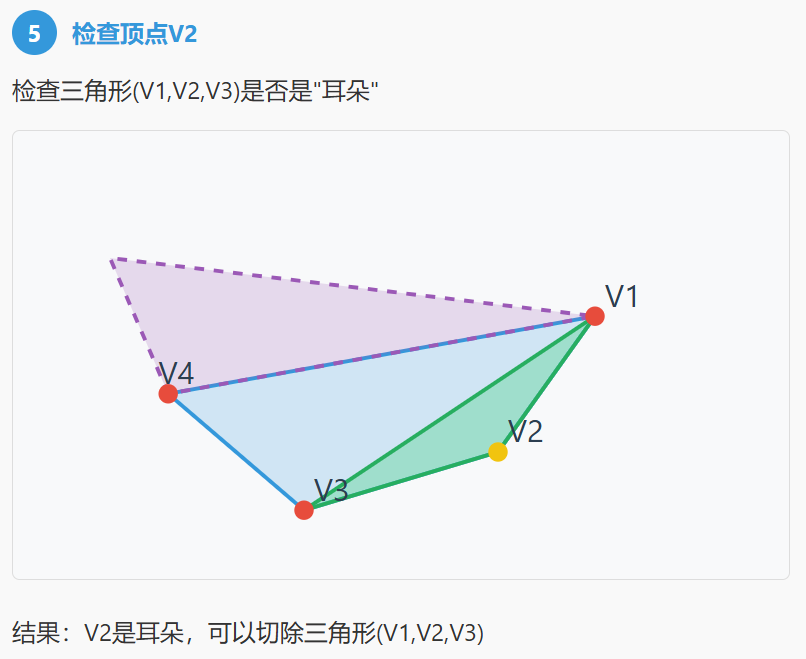
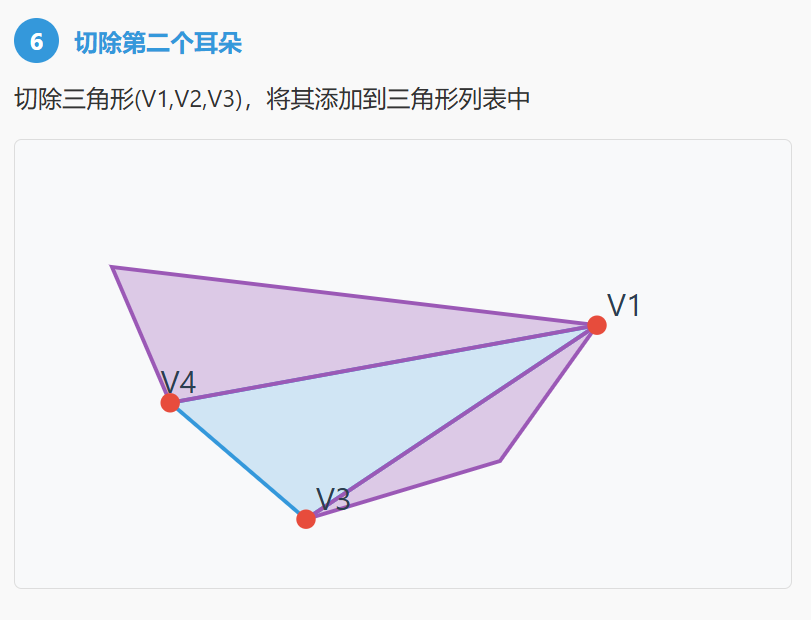
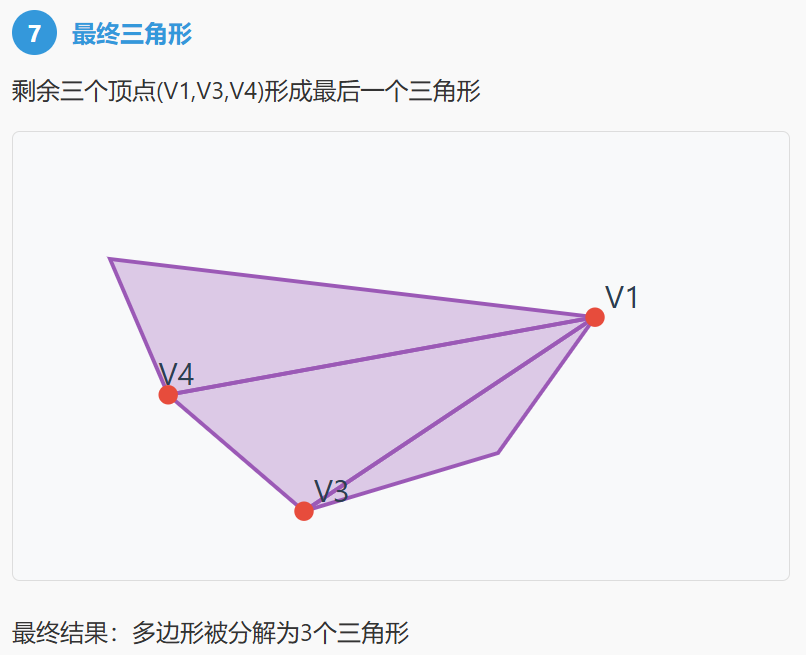
三、算法步骤：

预处理：
- 确保多边形的顶点是按逆时针顺序排列的（通常使用鞋带公式判断和调整）。
- 创建一个包含所有顶点索引的链表或列表。
寻找并剪裁耳朵：
- 遍历当前的顶点列表，对于每个顶点 V(i)，检查由其前一个顶点 V(i-1)、自身 V(i) 和后一个顶点 V(i+1) 构成的三角形是否是一个"耳朵"。
  - 凸性检查 ：检查顶点 V(i) 是否是一个凸顶点（通常用叉积判断）。
  - 空腔检查：检查这个三角形内部是否不包含多边形的任何其他顶点。
- 如果它是一个耳朵：
  - 将三角形 (i-1, i, i+1) 添加到结果三角形列表中。
  - 将顶点 V(i) 从顶点列表中移除。这相当于"剪掉"了这个耳朵，原来的多边形减少了一个顶点。
- 继续遍历剩下的顶点，重复"寻找-剪裁"的过程。
终止条件：
- 当顶点列表中只剩下3个顶点时，将最后这个三角形加入结果列表。
- 算法结束。

cs 复制代码

public class EarClippingTriangulator
{
    // 主函数：将多边形三角剖分，返回三角形顶点索引列表
    public static List<int> Triangulate(List<Vector2> points)
    {
        if (points == null || points.Count < 3)
            throw new ArgumentException("多边形至少需要3个顶点");

        // 创建顶点索引列表
        List<int> indices = new List<int>();
        for (int i = 0; i < points.Count; i++)
        {
            indices.Add(i);
        }

        List<int> triangles = new List<int>();

        // 处理多边形（可能是顺时针或逆时针）
        if (!IsCounterClockwise(points))
        {
            indices.Reverse();
        }

        // 耳切法主循环
        while (indices.Count > 3)
        {
            bool earFound = false;

            for (int i = 0; i < indices.Count; i++)
            {
                int prevIndex = GetPreviousIndex(i, indices.Count);
                int currentIndex = i;
                int nextIndex = GetNextIndex(i, indices.Count);

                Vector2 a = points[indices[prevIndex]];
                Vector2 b = points[indices[currentIndex]];
                Vector2 c = points[indices[nextIndex]];

                // 检查是否是凸顶点
                if (IsConvex(a, b, c))
                {
                    // 检查是否是"耳"（没有其他顶点在三角形内）
                    bool isEar = true;
                    for (int j = 0; j < indices.Count; j++)
                    {
                        if (j == prevIndex || j == currentIndex || j == nextIndex)
                            continue;

                        Vector2 testPoint = points[indices[j]];
                        if (IsPointInTriangle(testPoint, a, b, c))
                        {
                            isEar = false;
                            break;
                        }
                    }

                    if (isEar)
                    {
                        // 找到耳朵，添加三角形
                        triangles.Add(indices[prevIndex]);
                        triangles.Add(indices[currentIndex]);
                        triangles.Add(indices[nextIndex]);

                        // 移除当前顶点（耳朵尖端）
                        indices.RemoveAt(currentIndex);
                        earFound = true;
                        break;
                    }
                }
            }

            if (!earFound)
            {
                throw new InvalidOperationException("无法完成三角剖分 - 多边形可能自交或不是简单多边形");
            }
        }

        // 添加最后一个三角形
        if (indices.Count == 3)
        {
            triangles.Add(indices[0]);
            triangles.Add(indices[1]);
            triangles.Add(indices[2]);
        }

        return triangles;
    }

    // 鞋带公式判断多边形顶点顺序是否为逆时针
    private static bool IsCounterClockwise(List<Vector2> points)
    {
        float area = 0;
        for (int i = 0; i < points.Count; i++)
        {
            Vector2 current = points[i];
            Vector2 next = points[(i + 1) % points.Count];
            area += (current.x * next.y) - (next.x * current.y);
        }
        return area > 0; 
    }

    // 判断三点是否形成凸角
    private static bool IsConvex(Vector2 a, Vector2 b, Vector2 c)
    {
        return CrossProduct(b - a, c - b) > 0;
    }

    // 计算叉积
    private static float CrossProduct(Vector2 a, Vector2 b)
    {
        return a.x * b.y - a.y * b.x;
    }

    // 判断点是否在三角形内
    private static bool IsPointInTriangle(Vector2 p, Vector2 a, Vector2 b, Vector2 c)
    {
        // 使用重心坐标法
        float area = CrossProduct(b - a, c - a);
        float alpha = CrossProduct(b - p, c - p) / area;
        float beta = CrossProduct(c - p, a - p) / area;
        float gamma = 1 - alpha - beta;

        return alpha >= 0 && beta >= 0 && gamma >= 0;
    }

    // 获取前一个索引（循环）
    private static int GetPreviousIndex(int currentIndex, int count)
    {
        return (currentIndex - 1 + count) % count;
    }

    // 获取下一个索引（循环）
    private static int GetNextIndex(int currentIndex, int count)
    {
        return (currentIndex + 1) % count;
    }
}