ARConv：用于遥感全色锐化的自适应矩形卷积

摘要

https://arxiv.org/pdf/2503.00467

近年来，基于卷积神经网络（CNN）的遥感全色锐化技术在图像质量提升方面取得了显著进展。然而，这些方法中传统的卷积模块存在两个关键缺陷。首先，卷积操作中的采样位置被限制在一个固定的方形窗口内。其次，采样点的数量是预设且固定不变的。鉴于遥感图像中物体尺寸的多样性，这些僵化的参数导致特征提取效果欠佳。为了克服这些限制，我们提出了一种创新的卷积模块------自适应矩形卷积（ARConv）。ARConv 能够自适应地学习卷积核的高度和宽度，并根据学习到的尺度动态调整采样点的数量。这种方法使 ARConv 能够有效地捕获图像中不同物体的尺度特异性特征，从而优化卷积核大小和采样位置。此外，我们提出了 ARNet，一种以 ARConv 为主要卷积模块的网络架构。在多个数据集上的广泛评估表明，我们的方法在全色锐化性能上优于先前技术。消融实验和可视化结果进一步证实了 ARConv 的有效性。源代码将在 https://github.com/WangXueyang-uestc/ARconv.git 上提供。

1. 引言

清晰的遥感图像在军事、农业等多个领域至关重要。然而，现有技术只能捕获低分辨率多光谱图像（LRMS）和高分辨率全色图像（PAN）。LRMS 提供了丰富的光谱信息但空间分辨率低，而 PAN 图像虽然空间细节丰富，但仅限于灰度且缺乏光谱信息。

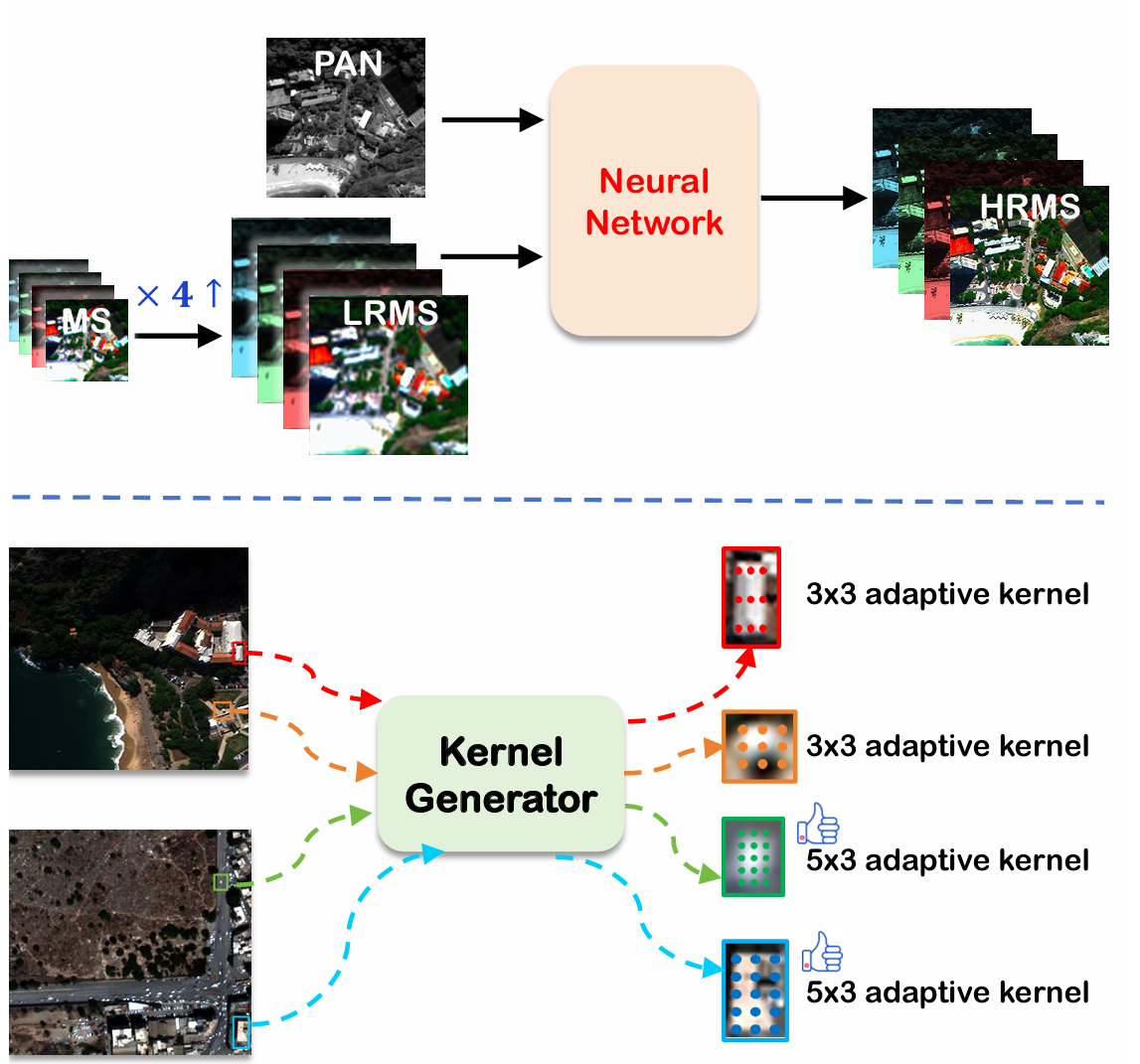
图 1. 上排：基于深度学习的遥感全色锐化流程图。下排：我们提出的自适应矩形卷积（ARConv）示意图，其拥有两个显著优势：1）其卷积核可以根据物体尺寸自适应修改采样位置；2）采样点的数量在不同特征图间动态确定，例如实现一个 5×3 的自适应矩形卷积，据我们所知，这是首次尝试。

全色锐化的目标是融合这两类图像以产生高分辨率多光谱图像（HRMS），如图 1 所示。目前已提出了许多全色锐化方法[20]，包括传统方法和基于深度学习的方法，其中传统方法又可进一步分为分量替换（CS）[4, 28]、多分辨率分析（MRA）[30, 32] 和变分优化（VO）[11, 26]。近年来，深度学习在图像处理领域的显著进展导致了许多基于卷积神经网络的全色锐化方法的广泛应用。与传统方法相比，这些方法主要通过卷积核提取输入 PAN 和 LRMS 图像的特征。然而，标准卷积有两个主要缺点。首先，其采样位置被限制在一个确定尺寸的方形窗口内，这限制了其变形能力，从而无法自适应地寻找采样位置。其次，卷积核的采样点数量是预先确定的，难以自适应地捕获不同尺度的特征。在遥感图像中，不同物体（如小汽车和大型建筑物）之间的尺度差异可能很大，而标准卷积不擅长捕获这些差异，导致特征提取效率低下。

近年来，许多创新的卷积方法被提出用于全色锐化。空间自适应卷积方法，如 PAC [25]、DDF [40]、LAGConv [16] 和 CANConv [9]，可以根据不同的空间位置自适应生成不同的卷积核参数，使它们能够适应不同的空间区域。然而，这些方法尚未充分考虑遥感图像中丰富的尺度信息。形状自适应卷积，如可变形卷积 [5, 41]，可以通过学习偏移量来自适应地调整每个采样点的位置，以提取不同形状物体的特征。虽然这提供了很大的灵活性，但可学习参数的数量随卷积核尺寸呈平方增长，使得在小数据集（例如图像锐化任务）上难以收敛。此外，它不能根据卷积核的形状调整采样点的数量，这进一步限制了其性能。多尺度卷积，如金字塔卷积 [10]，可以在同一特征图中提取不同尺度的信息。然而，它们的卷积核尺寸是预先确定的，而图像中的特征在不同尺度上可能表现出不同的模式和结构。这可能导致尺度间的特征融合不精确，可能影响模型的整体性能。

基于上述分析，我们提出了自适应矩形卷积（ARConv），它不仅可以自适应调整采样位置，还可以调整采样点的数量，如图 1 所示。前者通过仅学习两个参数（卷积核的高度和宽度）来实现，且不随卷积核尺寸增加而产生额外的计算负担。后者则根据学习到的高度和宽度的平均水平选择合适的采样点数量。此外，我们还为 ARConv 引入了仿射变换，从而带来了空间自适应性。所有这些使得我们的模块能够有效地从特征图中提取不同尺寸物体的特征。本文的主要贡献概述如下：

1. 提出了 ARConv 模块，它能够自适应地调整采样位置并改变采样点数量，从而有效地捕获遥感图像中各种物体的尺度特异性特征。基于 ARConv 和 U-net 架构 [23, 35]，引入了 ARNet。
2. 通过热力图可视化，探索了学习到的卷积核高度和宽度与实际物体尺寸之间的关系。观察到了一定程度的相关性，这验证了所提方法的有效性。
3. 通过在多个数据集上与各种全色锐化方法进行比较，验证了 ARConv 的有效性。结果表明 ARConv 实现了出色的性能。

2. 相关工作

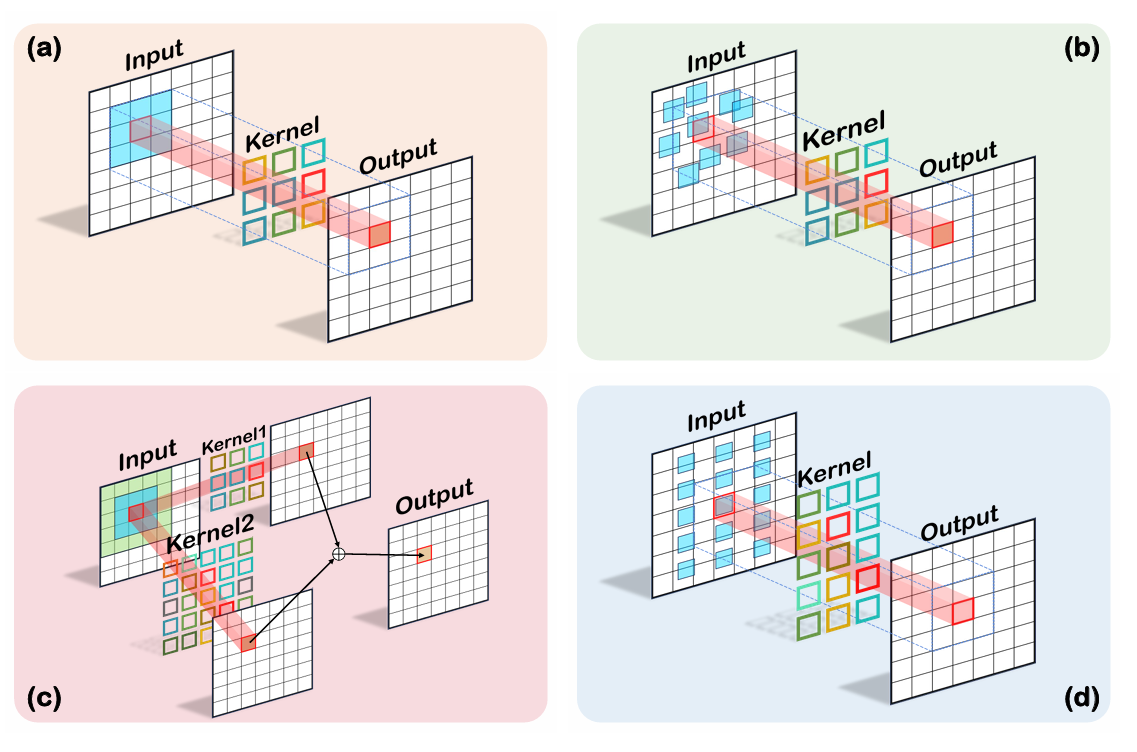
图 2. 四种类型卷积核工作原理示意图。(a) 标准卷积。(b) 可变形卷积 [5, 41]。(c) 多尺度卷积 [10, 18]。(d) 我们提出的卷积（ARConv）。

2.1. 自适应卷积

标准卷积因其固定的形状和尺寸，在处理几何变换时灵活性有限，难以适应视觉任务中常见的物体尺度与形状变化。可变形卷积 [5, 41] 首次通过为每个像素学习一个偏移矩阵来调整采样位置，从而解决了这一限制，如图 2 所示。这一进展首次使卷积核能够以无监督的方式变形。基于可变形卷积的概念，动态蛇形卷积 [22] 通过采用精心设计的损失约束来引导卷积核的变形，专门针对管状结构的特征提取进行了优化。尺度自适应卷积 [39] 通过允许卷积核学习缩放比，动态修改感受野，从而扩展了这种灵活性，以更好地捕获不同尺度的特征。

在上述卷积中，变形要么变得过于灵活，在处理大量采样点时导致计算负担增加；要么过于僵化，难以捕获不规则形状物体的特征。此外，采样点的数量是预先确定的，无法根据卷积核学习到的形状动态调整。

2.2. 多尺度卷积

多尺度卷积通过使用不同尺寸的卷积核来增强对输入数据的分析，从而促进提取不同尺度的特征信息。相比之下，标准卷积仅限于捕获单一尺度的特征。金字塔卷积（PyConv）[10] 通过在每个层内采用分层结构，利用不同尺度的卷积核金字塔来全面处理输入特征图，从而解决了这一限制，如图 2 所述。为了提高计算效率并减少总参数量，每个卷积核的深度（即参与卷积操作的通道数）根据金字塔层级自适应调整。选择性核网络 [18] 进一步改进了这种方法，通过结合一个软注意力机制，动态选择从多尺度卷积生成的最相关特征图，从而增加了网络对空间分辨率变化的适应性。然而，这些卷积模块仍然无法根据特征图中各种物体的大小自适应地调整卷积核的采样位置和采样点数量。

2.3. 动机

遥感图像在内容上表现出相当大的多样性，物体尺寸差异显著。相比于使用固定尺寸的卷积核，使用不同尺寸的卷积核对于从不同区域提取特征更为有效。传统的形状自适应卷积可以修改采样位置以适应物体形状，但不能根据卷积核的形状调整采样点的数量。此外，一些变形策略需要学习很多参数，导致计算成本较高。虽然多尺度卷积可以在同一特征图中捕获各种尺度的特征，但其卷积核尺寸仍然是固定的，因此无法根据特征图内容自适应调整采样位置。为了克服这些限制，我们引入了自适应矩形卷积（ARConv），这是一种将卷积核的高度和宽度视为可学习参数的新模块。这允许卷积核的形状根据不同物体的大小动态调整。通过在矩形可变形区域内均匀分布采样点，ARConv 可以灵活修改采样位置，并根据每个特征图中学习到的卷积核的平均大小调整点的数量。与传统的可变形卷积 [5] 不同，我们的方法只需要学习两个参数，随着采样点数量的增加，计算开销最小。为了进一步增强适应性，我们对卷积核的输出应用仿射变换，以提高空间灵活性。

3. 方法

本节详述 ARConv 和 ARNet 的设计。ARConv 的实现遵循四个步骤：（1）学习卷积核的高度和宽度特征图。（2）选择卷积核采样点的数量。（3）生成采样图。（4）卷积的实现。在 ARNet 中，U-Net [23, 35] 的标准卷积层被替换为 ARConv 模块，以便更有效地为全色锐化任务捕获丰富的尺度信息。ARConv 的整体架构如图 3 所示。

3.1. 自适应矩形卷积

3.1.1. 学习卷积的高度和宽度

学习过程可以用数学公式表示为：

yi=fθi(X),i∈{1,2},\mathbf{y}{i}=f{\theta_{i}}(\mathbf{X}),\quad i\in\{1,2\},yi=fθi(X),i∈{1,2},

其中 X∈RH×W×Cin\mathbf{X}\in\mathbb{R}^{H\times W\times C_{in}}X∈RH×W×Cin 表示输入特征图。H 和 W 分别表示特征图的高度和宽度，CinC_{in}Cin 表示输入通道数。此外，fθi(⋅)f_{\theta_{i}}(\cdot)fθi(⋅) 对应两个负责预测卷积核高度和宽度的子网络，每个子网络由两部分组成：一个共享特征提取器和具有参数 θi\theta_{i}θi 的独立高度-宽度学习器。输出特征图表示为 yi  ∈  RH×W×1\mathbf{y}{i}\;\in\;\mathbb{R}^{H\times W\times1}yi∈RH×W×1 ，其中 y1\mathbf{y}{1}y1 是高度特征图，y2\mathbf{y}{2}y2 是宽度特征图，在图 3 中分别称为 h 和 w。高度-宽度学习器的最后一层是 Sigmoid 函数，其中 Sigmoid⁡(x)=11+e−x.So⁡,yi∈(0,1)\begin{array}{r}{\operatorname{Sigmoid}(x)=\frac{1}{1+e^{-x}}.\quad\operatorname{So},\mathbf{y}{i}\in(0,1)}\end{array}Sigmoid(x)=1+e−x1.So,yi∈(0,1) ，它们仅代表相对大小，因此不能直接对应卷积核的高度和宽度，我们采用以下方法来约束它们的取值范围。

yi=ai⋅yi+bi,i∈{1,2},\mathbf{y}{i}=a{i}\cdot\mathbf{y}{i}+b{i},\quad i\in\{1,2\},yi=ai⋅yi+bi,i∈{1,2},

其中 aia_{i}ai 和 bib_{i}bi 是调制因子，用于约束高度和宽度的范围。因此，卷积核的高度被约束在范围 (b1,a1+b1)(b_{1},a_{1}+b_{1})(b1,a1+b1) 内，宽度被约束在范围 (b2,a2+b2)(b_{2},a_{2}+b_{2})(b2,a2+b2) 内。

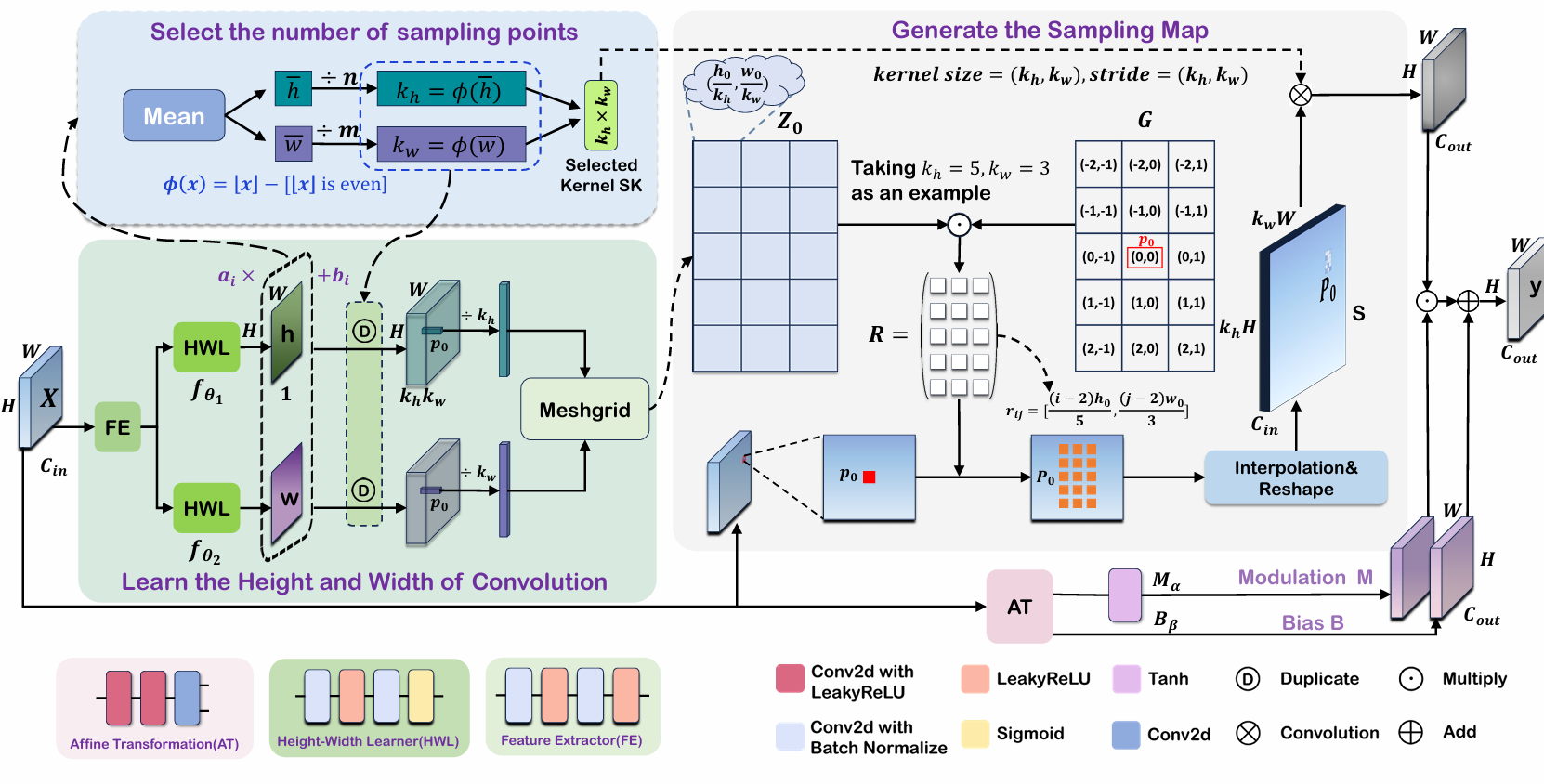
图 3. ARConv 架构概览。该模块包含四个主要部分。第一部分处理卷积核高度和宽度的学习过程。第二部分关注卷积核采样点数量的选择过程。第三部分以网格中心位置 p0\mathbf{p}_{0}p0 为例模拟采样图 S 的生成过程。最后部分描述了 ARConv 的卷积操作过程。

高度和宽度的特征图被送入第二部分（稍后将详述），在那里选择卷积核的采样点数量 kh⋅kwk_{h}\cdot k_{w}kh⋅kw。每个高度和宽度特征图随后被复制 kh⋅kwk_{h}\cdot k_{w}kh⋅kw 次。接着，应用网格化操作生成每个像素位置 (i,j)(i,j)(i,j) 处卷积核形状的缩放矩阵 Zij∈Rkh×kwZ_{i j}\in\mathbb{R}^{k_{h}\times k_{w}}Zij∈Rkh×kw。

3.1.2. 选择采样点的数量

首先，我们计算 y1\mathbf{y}{1}y1 和 y2\mathbf{y}{2}y2 中所有值的均值，以获得学习到的高度和宽度的平均水平。然后，卷积核在垂直和水平方向上的采样点数量由下式得出：kh = ϕ(⌊yˉ1n⌋),kw = ϕ(⌊yˉ2m⌋)\begin{array}{r}{k_{h}\:=\:\phi\big(\lfloor\frac{\bar{\mathbf{y}}{1}}{n}\rfloor\big),k{w}\:=\:\phi\big(\lfloor\frac{\bar{\mathbf{y}}_{2}}{m}\rfloor\big)}\end{array}kh=ϕ(⌊nyˉ1⌋),kw=ϕ(⌊myˉ2⌋) ，其中 ⌊x⌋\lfloor x\rfloor⌊x⌋ 表示 x 的下取整，m 和 n 表示将卷积核的高度和宽度映射到采样点数量的调制系数。函数 ϕ(⋅)\phi(\cdot)ϕ(⋅) 可以表示如下：

ϕ(x)=x−[x  is  even],\phi(x)=x-[x\;\mathrm{is\;even}],ϕ(x)=x−[xiseven],

这里，[.] 表示艾弗森括号。给定固定的卷积核高度和宽度，m 和 n 的值越大，采样点越少，分布越稀疏。根据等式 (3)，我们只选择采样点数为奇数的卷积核。当 ⌊yˉ1n⌋or⌊yˉ2m⌋\left\lfloor{\frac{\bar{\mathbf{y}}{1}}{n}}\right\rfloor{\mathrm{or}}\left\lfloor{\frac{\bar{\mathbf{y}}{2}}{m}}\right\rfloor⌊nyˉ1⌋or⌊myˉ2⌋ 为偶数时，我们选择比该偶数小的最近奇数。最后，采样点数量为：

N=kh⋅kw.N=k_{h}\cdot k_{w}.N=kh⋅kw.

3.1.3. 生成采样图

在标准卷积中，过程涉及使用规则网格 G 从输入特征图 X\mathbf{X}X 中采样，然后将这些采样值与权重 w 进行加权求和。例如，

G={(−1,−1),(−1,0),⋯ ,(1,0),(1,1)},\mathbf{G}=\{(-1,-1),(-1,0),\cdots,(1,0),(1,1)\},G={(−1,−1),(−1,0),⋯,(1,0),(1,1)},

对应一个在输入图上覆盖 3×3 区域且采样点之间无间隔的卷积核。

形式上，一个位置 p0\mathbf{p}_{0}p0 的标准卷积操作可以表示为，

y(p0)=∑gn∈Gw(gn)⋅x(p0+gn),\mathbf{y}(\mathbf{p}{0})=\sum{\mathbf{g}{n}\in\mathbf{G}}\mathbf{w}(\mathbf{g}{n})\cdot\mathbf{x}(\mathbf{p}{0}+\mathbf{g}{n}),y(p0)=gn∈G∑w(gn)⋅x(p0+gn),

其中 y 是输出特征图，w 表示卷积核的参数，gn\mathbf{g}{n}gn 表示网格 G 相对于位置 p0\mathbf{p}{0}p0 的偏移。

对于 ARConv，我们使用 G∈Rkh×kw\mathbf{G}\in\mathbb{R}^{k_{h}\times k_{w}}G∈Rkh×kw 表示卷积核尺寸为 kh×kwk_{h}\times k_{w}kh×kw 的标准卷积的偏移矩阵，该矩阵在所有像素间共享。G 中第 i 行第 jjj 列的元素，记为 gijg_{i j}gij，定义为：

gij=(2i−kh−12,2j−kw−12).g_{i j}=\left(\frac{2i-k_{h}-1}{2},\frac{2j-k_{w}-1}{2}\right).gij=(22i−kh−1,22j−kw−1).

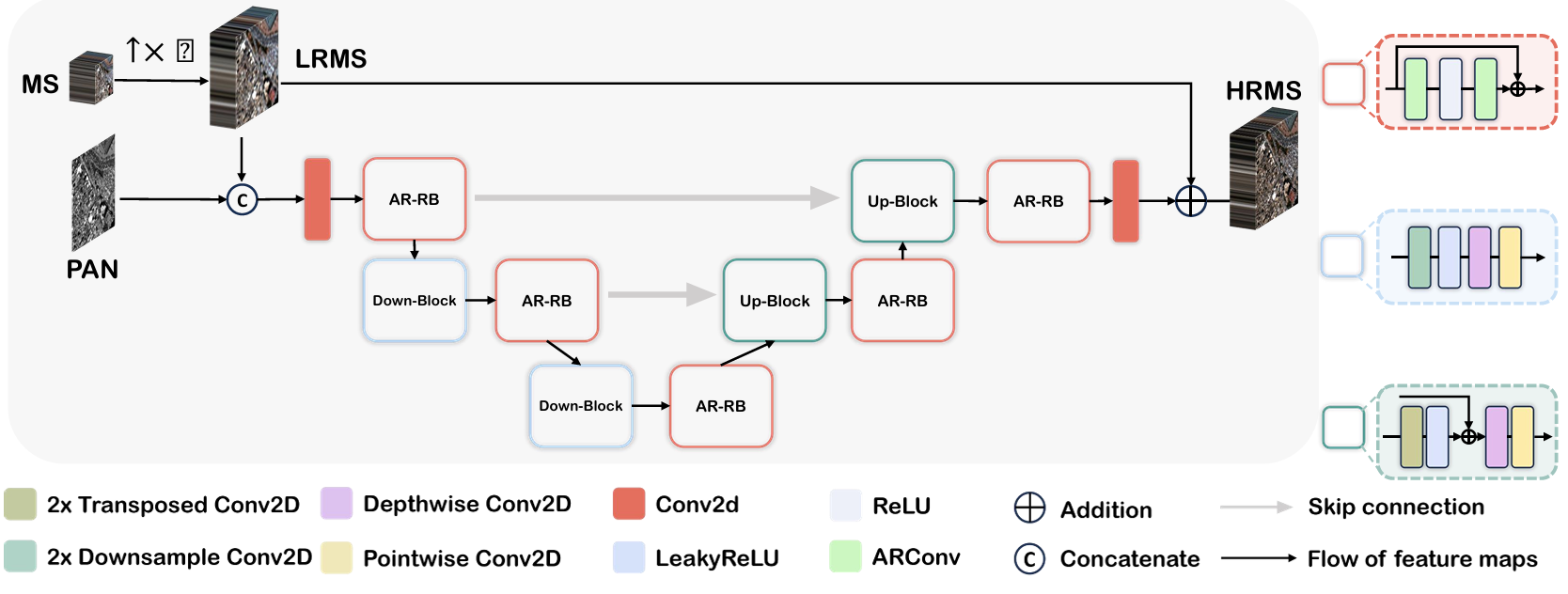
图 4. ARNet 的整体架构。ARNet 将 U-Net 中 Resblock 的标准卷积替换为 ARConv，创建了 ARResblock。模型包含下采样块用于提取高级特征，以及使用转置卷积恢复空间分辨率的上采样块。跳跃连接有助于传递详细的空间信息。

接下来，我们定义 Z0∈Rkh×kw\mathbf{Z}{0}\in\mathbb{R}^{k{h}\times k_{w}}Z0∈Rkh×kw 为位置 p0\mathbf{p}{0}p0 处的尺度矩阵，该矩阵在第一步中计算得出。Z0\mathbf{Z}{0}Z0 中第 i 行第 j 列的元素，记为 zijz_{i j}zij，由下式给出：

zij=(h0kh,w0kw),z_{i j}=\left(\frac{h_{0}}{k_{h}},\frac{w_{0}}{k_{w}}\right),zij=(khh0,kww0),

其中 h0h_{0}h0 和 w0w_{0}w0 分别表示在位置 p0\mathbf{p}{0}p0 学习到的卷积核的高度和宽度。ARConv 在位置 p0\mathbf{p}{0}p0 处的偏移矩阵，记为 R\mathbf{R}R，随后计算为：

R=Z0⊙G,\mathbf{R}=\mathbf{Z}_{0}\odot\mathbf{G},R=Z0⊙G,

其中 ⊙\odot⊙ 表示逐元素乘法。R 中第 i 行第 jjj 列的元素，记为 rijr_{i j}rij，由下式给出：

rij=((2i−kh−1)h02kh,(2j−kw−1)w02kw).r_{i j}=\left(\frac{(2i-k_{h}-1)h_{0}}{2k_{h}},\frac{(2j-k_{w}-1)w_{0}}{2k_{w}}\right).rij=(2kh(2i−kh−1)h0,2kw(2j−kw−1)w0).

显然，在大多数情况下，采样点不与网格中心重合。因此，需要进行插值来估计它们的像素值。在此背景下，我们采用双线性插值，其数学公式如下：

t(x,y)=wxTTwy,\mathbf{t}(x,y)=\mathbf{w}{x}^{\mathrm{T}}\mathbf{T}\mathbf{w}{y},t(x,y)=wxTTwy,

其中 t(x,y)\mathbf{t}(x,y)t(x,y) 表示坐标 (x,y)(x,y)(x,y) 处的像素值。

T=(t(x0,y0)t(x0,y1)t(x1,y0)t(x1,y1)),\mathbf{T}=\left(\begin{matrix}{\mathbf{t}(x_{0},y_{0})}&{\mathbf{t}(x_{0},y_{1})}\\ {\mathbf{t}(x_{1},y_{0})}&{\mathbf{t}(x_{1},y_{1})}\end{matrix}\right),T=(t(x0,y0)t(x1,y0)t(x0,y1)t(x1,y1)),

其中 (x0,y0),(x0,y1),(x1,y0),(x1,y1)(x_{0},y_{0}),(x_{0},y_{1}),(x_{1},y_{0}),(x_{1},y_{1})(x0,y0),(x0,y1),(x1,y0),(x1,y1) 是离 (x,y)(x,y)(x,y) 最近的四个网格点的坐标。

wx=(1−wxwx),wy=(1−wywy),\mathbf{w}{x}=\left(\begin{matrix}{1-w{x}}\\ {w_{x}}\end{matrix}\right),\mathbf{w}{y}=\left(\begin{matrix}{1-w{y}}\\ {w_{y}}\end{matrix}\right),wx=(1−wxwx),wy=(1−wywy),

其中 wx=x−x0x1−x0,wy=y−y0y1−y0\begin{array}{r}{w_{x}=\frac{x-x_{0}}{x_{1}-x_{0}},w_{y}=\frac{y-y_{0}}{y_{1}-y_{0}}}\end{array}wx=x1−x0x−x0,wy=y1−y0y−y0 ，它们分别代表 x 方向和 y 方向上的归一化插值权重。

总而言之，我们提出的卷积操作可以用数学公式表示为：

y(p0)=∑rn∈Rw(rn)⋅t(p0+rn),\mathbf{y}(\mathbf{p}{0})=\sum{\mathbf{r}{n}\in\mathbf{R}}\mathbf{w}(\mathbf{r}{n})\cdot\mathbf{t}(\mathbf{p}{0}+\mathbf{r}{n}),y(p0)=rn∈R∑w(rn)⋅t(p0+rn),

其中 y(p0)\mathbf{y}(\mathbf{p}{0})y(p0) 指的是输出特征图 y\mathbf{y}y 中位置 p0\mathbf{p}{0}p0 处的像素值，w 表示卷积核的参数，rn\mathbf{r}{n}rn 枚举 R 中的元素，t(p0+rn)\mathbf{t}(\mathbf{p}{0}+\mathbf{r}{n})t(p0+rn) 计算位置 p0+rn\mathbf{p}{0}+\mathbf{r}_{n}p0+rn 处的像素值。

无论是使用标准卷积还是我们的方法，图像中的每个像素在卷积操作期间都对应一个采样窗口。在标准卷积中，采样点都位于网格中心，采样窗口只是简单地以固定步长滑过图像。然而，在 ARConv 中，每个像素的采样窗口大小各不相同，使得传统方法不再适用。在实践中，我们不是为每个像素生成一个唯一的卷积核，而是采用一种等效的方法。我们采用一种扩展技术，提取每个像素对应采样窗口的采样点位置处的值，并将它们组合成一个新的网格 P0\mathbf{P}{0}P0，以取代原始像素 p0\mathbf{p}{0}p0，其中 P0  ∈∼  Rkh×kw×Cin,  p∼0  ∈  R1×1×C~in\mathbf{P}{0}\;\stackrel{\sim}{\in}\;\mathbb{R}^{k{h}\times k_{w}\times C_{in}},\;\stackrel{\sim}{\mathbf{p}}{0}\;\in\;\mathbb{R}^{1\times1\times\widetilde{C}{in}}P0∈∼Rkh×kw×Cin,p∼0∈R1×1×C in。完成对每个像素的扩展后，我们得到最终的采样图 S，其属于 R(khH)×(kwW)×Cin\mathbb{R}^{(k_{h}H)\times(k_{w}W)\times C_{in}}R(khH)×(kwW)×Cin。

3.1.4. 卷积的实现

在这一部分，我们对 S 应用卷积进行特征提取，使用的卷积核尺寸和步长均设置为 (kh,kw)(k_{h},k_{w})(kh,kw)。为了引入空间自适应性，我们对输出特征图应用仿射变换。我们使用两个子网络，Mα\mathbf{M}{\alpha}Mα 和 Bβ\mathbf{B}{\beta}Bβ，来预测仿射变换的矩阵 M 和 B，其中 α 和 β 是这些网络的参数。最终输出特征图由下式给出：

y=SK⊗S⊙M⊕B,\mathbf{y}=\mathbf{S}\mathbf{K}\otimes\mathbf{S}\odot\mathbf{M}\oplus\mathbf{B},y=SK⊗S⊙M⊕B,

其中 y∈RH×W×Cout\mathbf{y}\in\mathbb{R}^{H\times W\times C_{out}}y∈RH×W×Cout 是输出特征图。SK∈\mathbf{S K}\inSK∈ RCin×k˘h×kw×Cout\mathbb{R}^{C_{in}\times\breve{\boldsymbol{k}}{h}\times\boldsymbol{k}{w}\times C_{out}}RCin×k˘h×kw×Cout 是所选卷积核的参数，⊗\otimes⊗ 表示卷积操作，⊙\odot⊙ 表示逐元素乘法，⊕ 表示逐元素加法。

3.2. ARNet 架构

本节详述 ARNet 的构建，如图 4 所示。我们的网络灵感来源于 U-net 架构 [23, 35]，这是一种在图像分割中众所周知的模型，它使用编码器-解码器结构并带有跳跃连接以保留空间信息。在 ARNet 中，我们将 ResBlock [14] 中的标准卷积层替换为我们的 ARConv。数据流如下：首先，将 MS 图像上采样以匹配 PAN 图像的分辨率，生成 LRMS 图像。接下来，将 PAN 和 LRMS 图像沿通道维度拼接并输入网络。ARNet 涉及一系列下采样和上采样步骤，不同深度的 ARConv 层自适应地寻找不同尺度特征提取的最佳参数。最后，将学习到的细节信息注入到 LRMS 图像中 [6, 15]，对其进行精炼，并产生具有增强分辨率和细节的最终输出图像。

4. 实验

4.1. 数据集、评估指标与训练细节

我们在多个数据集上评估我们方法的有效性，包括 WorldView3（WV3）传感器捕获的 8 波段数据，以及 QuickBird（QB）和高分二号（GF2）传感器捕获的 4 波段数据。尽管我们采用监督学习方法，但直接获取地面真值数据很困难，因此我们应用 Wald 协议 [7, 34] 来构建我们的数据集。所有三个数据集都可以从公共存储库 [8] 获取。对于不同分辨率的测试集，我们使用不同的评估指标。具体来说，我们使用 SAM[3]、ERGAS[33] 和 Q8[13] 来评估 ARNet 在降分辨率数据集上的性能，并使用 Ds,DλD_{s},D_{\lambda}Ds,Dλ 和 HQNR [2] 来评估其在全分辨率数据集上的性能。在训练期间，我们采用 l1l_{1}l1 损失函数和 Adam 优化器 [17]，批量大小为 16。鉴于我们的方法涉及根据学习到的高度和宽度选择卷积核------这种方法可能使收敛复杂化------我们将前 100 个周期指定为探索阶段。在此阶段，我们允许模型探索不同的配置。在这 100 个周期之后，我们根据得到的结果从 16 个批次中随机选择一个卷积核组合，然后在剩余的培训中固定该选择。关于数据集和训练过程的更多细节在补充材料第 6.1 节和第 6.2 节中提供。

4.2. 结果

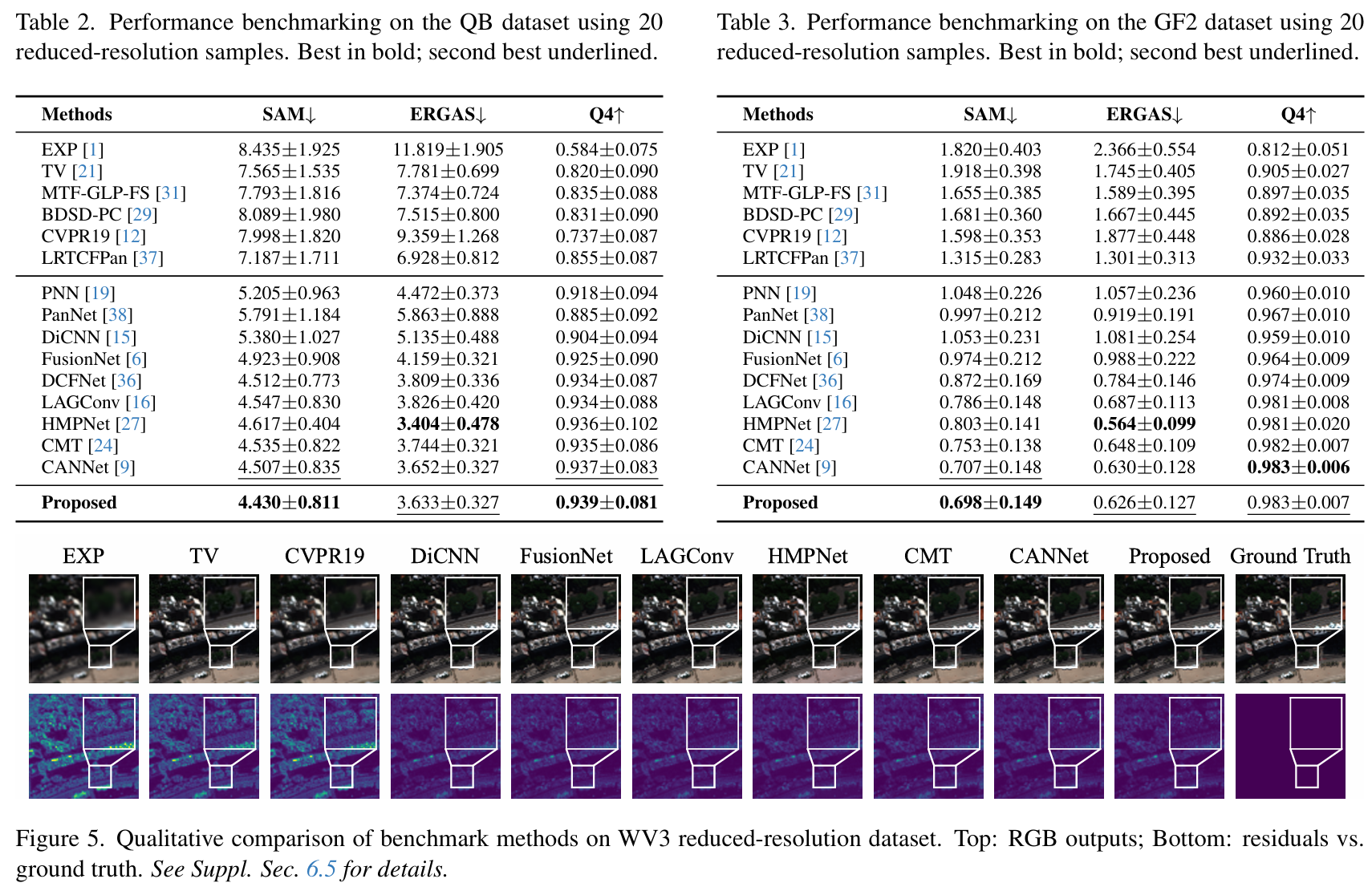
ARNet 的出色性能通过在 WV3、QB 和 GF2 基准数据集上的全面评估得到了充分证明。表 1 至 3 详细比较了 ARNet 与各种最先进技术，包括传统方法、通用深度学习方法以及与我们提出的工作类似的专用卷积深度学习方法，例如 LAGConv [16] 和 CANConv [9]，更多细节可在补充材料第 6.3 节中找到。结果清楚地表明，ARNet 在不同数据集上始终提供高质量的性能，显示出显著的鲁棒性。此外，视觉评估表明，ARNet 生成的图像最接近地面真值，说明我们的卷积方法能够有效适应不同的物体大小并在适当的尺度上提取特征。关于基准测试和视觉示例的更多细节，请参阅补充材料第 6.5 节。

4.3. 消融实验

为了评估 ARConv 中不同组件的影响，我们通过选择性移除某些模块进行了消融实验：（a）无高度和宽度自适应，（b）无采样点数量自适应，以及（c）无仿射变换。结果如表 4 所示。（a）和（b）中的性能下降突显了 ARConv 在适应不同物体尺寸方面的有效性。在（c）中，性能的急剧下降表明我们的变形策略灵活性有限，而通过仿射变换引入空间自适应性有效地缓解了这个问题。值得注意的是，这种变换的计算成本并不随卷积核尺寸增加而增加。
表 4. 在 WV3 降分辨率数据集上的消融研究：HWA（高度和宽度自适应）、NSPA（采样点自适应）、AT（仿射变换）。

|------------|-------------|-------------|-------------|
| 方法 | SAM↓ | ERGAS↓ | Q8↑ |
| (a) 无 HWA | 2.925±0.593 | 2.171±0.557 | 0.920±0.085 |
| (b) 无 NSPA | 2.911±0.603 | 2.152±0.565 | 0.921±0.083 |
| (c) 无 AT | 3.020±0.614 | 2.269±0.562 | 0.916±0.085 |
| Proposed | 2.885±0.590 | 2.139±0.528 | 0.921±0.083 |

4.4. 讨论

不同的高度和宽度学习范围 ：为了评估不同卷积核高度和宽度对 ARNet 性能的影响，我们设计了五组实验，高度和宽度范围分别为：(a) 1-3, (b) 1-9, © 1-18, (d) 1-36, 和 (e) 1-63。在 (a) 中，卷积核尺寸固定为 3×3，而在 (b) 到 (e) 中，最大卷积核尺寸为 7×77\times77×7。如表 5 所示，ARNet 的性能起初随着高度和宽度范围的增加而提高，但在超出 © 情况下的最佳设置后开始下降。这种模式的出现是因为较小的范围导致采样点密集，捕获过多噪声；而较大的范围使采样点分布过于稀疏，降低了卷积核捕获精细细节的能力。
表 5. 在 WV3 降分辨率数据集上，不同卷积核高度和宽度学习范围的性能。

方法	SAM↓	ERGAS↓	Q8↑
(a) 1-3	2.923±0.600	2.164±0.546	0.919±0.085
(b) 1-9	2.896±0.588	2.145±0.544	0.921±0.084
(c) 1-18	2.885±0.590	2.139±0.528	0.921±0.083
(d) 1-36	3.044±0.646	2.216±0.578	0.916±0.087
(e) 1-63	3.066±0.593	2.249±0.554	0.912±0.095

替换其他网络中的卷积模块：我们将 ARConv 作为一个即插即用的模块，替换了全色锐化网络（如 FusionNet [6]、LAGNet [16] 和 CANNet [9]）中的原始卷积层，以证明 ARConv 的有效性。表 6 的结果表明，ARConv 显著提升了这些网络的性能。关于该实验的更多细节在补充材料第 6.4 节中提供。
表6. 当用 ARConv 替换其他全色锐化方法中的卷积核时，在 WV3 降分辨率数据集上的性能。

|-----------------|-------------|-------------|-------------|
| 方法 | SAM↓ | ERGAS↓ | Q8↑ |
| FusionNet [6] | 3.325±0.698 | 2.467±0.645 | 0.904±0.090 |
| AR-FusionNet | 3.171±0.650 | 2.395±0.630 | 0.911±0.087 |
| LAGNet [16] | 3.104±0.559 | 2.300±0.613 | 0.910±0.091 |
| AR-LAGNet | 3.083±0.643 | 2.277±0.547 | 0.916±0.085 |
| CANNet [9] | 2.930±0.593 | 2.158±0.515 | 0.920±0.084 |
| AR-CANNet | 2.885±0.590 | 2.139±0.528 | 0.921±0.083 |

卷积核可视化 ：图 6 显示了 ARNet 不同层的卷积核学习到的高度和宽度特征图。整体热力图揭示了 RGB 图像中各种物体的轮廓，尤其是在网络最外层的特征图中。虽然中间层看起来杂乱，但它们捕获了更深层的语义信息，例如 RGB 图像中的物体尺寸。例如，在第四层的高度热力图中，一个倾斜建筑物的轮廓隐约可见，边缘有一条细蓝线。这表明学习到的卷积核高度在边缘处较小，反映了卷积核对建筑物尺寸的适应。更多可视化内容请参阅补充材料第 6.6 节。

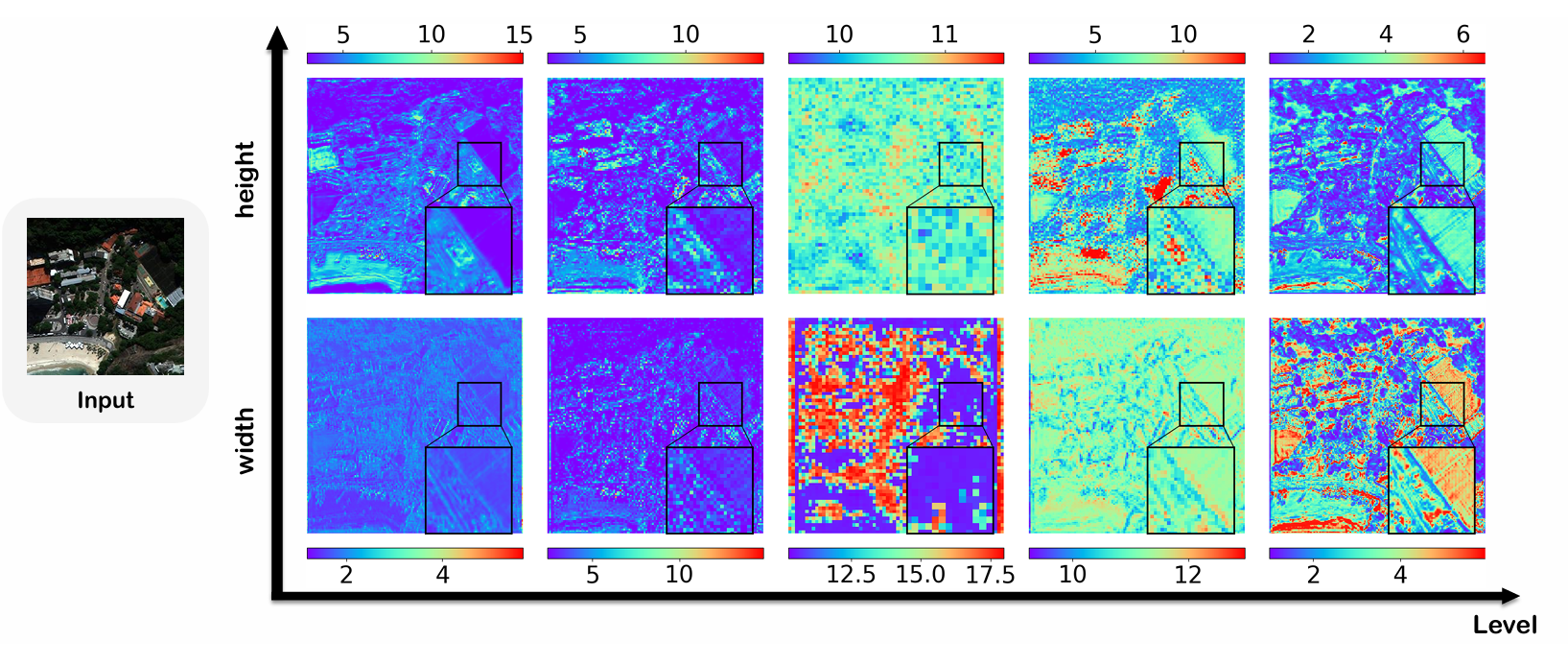
图 6. 不同层卷积核在每个像素处学习到的高度和宽度的热力图。输入图像是来自 WV3 数据集的样本。热力图中，不同颜色代表卷积核捕获的不同高度和宽度。

与 DCNv2 的比较：我们从 ARConv 中移除了仿射变换，并采用了与 DCNv2 [41] 相同的调制方法。两个模型都在 WV3 数据集上训练了 600 个周期。结果如表 7 所示，显然我们的性能超过了 DCNv2。这可能是因为 DCNv2 中的变形策略需要学习大量参数，这可能会阻碍锐化任务的收敛。
表 7. ARConv 与 DCNv2 在 WV3 降分辨率数据集上的性能比较。

|--------------|-------------|-------------|-------------|
| 方法 | SAM↓ | ERGAS↓ | Q8↑ |
| Ours | 2.881±0.590 | 2.149±0.531 | 0.921±0.084 |
| DCNv2 [41] | 3.151±0.679 | 2.425±0.656 | 0.915±0.083 |

5. 结论

总而言之，我们引入了一种自适应矩形卷积模块 ARConv，它可以根据输入图像中物体尺寸的变化，为每个像素动态学习高度和宽度自适应的卷积核。通过根据学习到的尺度调整采样点的数量，ARConv 克服了卷积核中固定采样形状和采样点数量的传统限制。ARConv 作为即插即用模块无缝集成到 U-net 中，形成了 ARNet，该网络在多个数据集上展现了出色的性能。此外，可视化研究证实，我们的卷积核可以根据物体的大小和形状有效调整其高度和宽度，为全色锐化任务提供了一种新颖的解决方案。

参考文献

1]Bruno Aazzi, Luciano Alparone, Stefano Baronti, and Andrea Garzelli. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote. Sens., 40:2300--2312, 2002. 6,7, 2, 3

2\]A. Arienzo, Gemine Vivone, Andrea Garzelli, Luciano Alparone, and Jocelyn Chanussot. Full resolution quality assessment of pansharpening: Theoretical and hands-on approaches. IEEE Geoscience and Remote Sensing Magazine, 10:168-201, 2022. 6 \[3\] Joseph W. Boardman. Automating spectral unmixing of aviris data using convex geometry concepts. 1993.6 \[4\]Jaewan Choi, Kiyun Yu, and Yongil Kim. A new adaptive component-substitution-based satellite image fusion by using partial replacement. IEEE Transactions on Geoscience and Remote Sensing, 49:295--309, 2011. 1 \[5\]Jifeng Dai, Haozhi Qi, Yuwen Xiong, Yi Li, Guodong Zhang, Han Hu, and Yichen Wei. Deformable convolutional networks. 2017 IEEE International Conference on Computer Vision (ICCV), pages 764--773, 2017.2,3 \[6\]Liang-Jian Deng, Gemine Vivone, Cheng Jin, and Jocelyn Chanussot. Detail injection-based deep convolutional neural networks for pansharpening. IEEE Transactions on Geoscience and Remote Sensing, 59:6995--7010, 2021. 6,7,8, 2, 3 \[7\]Liang-Jian Deng, Gemine Vivone, Cheng Jin, and Jocelyn Chanussot. Detail injection-based deep convolutional neural networks for pansharpening. IEEE Transactions on Geoscience and Remote Sensing, 59:6995--7010, 2021. 6 \[8\]Liang-Jian Deng, Gemine Vivone, Mercedes Eugenia Paoletti, Giuseppe Scarpa, Jiang He, Yongjun Zhang, Jocelyn Chanussot, and Antonio J. Plaza. Machine learning in pansharpening: A benchmark, from shallow to deep networks. IEEE Geoscience and Remote Sensing Magazine, 10:279--315, 2022. 6, 1 \[9\]Yule Duan, Xiao Wu, Haoyu Deng, and Liangjian Deng. Content-adaptive non-local convolution for remote sensing pansharpening. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 27738--27747, 2024. 2,6,7,8,3 \[10\]Ionut Cosmin Duta, Li Liu, Fan Zhu, and Ling Shao. Pyramidal convolution: Rethinking convolutional neural networks for visual recognition. ArXiv, abs/2006.11538, 2020. 2, 3 \[11\] Xueyang Fu, Zihuang Lin, Yue Huang, and Xinghao Ding. A variational pan-sharpening with local gradient constraints. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10257--10266, 2019. 1 \[12\]Xueyang Fu, Zihuang Lin, Yue Huang, and Xinghao Ding. A variational pan-sharpening with local gradient constraints. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10257--10266, 2019. 6,7,2, 3 \[13\]Andrea Garzelli and Filippo Nencini. Hypercomplex quality assessment of multi/hyperspectral images. IEEE Geoscience and Remote Sensing Letters, 6:662--665, 2009. 6 \[14\]Kaiming He, X. Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 770--778, 2015. 6 \[15\]Lin He, Yizhou Rao, Jun Yu Li, Jocelyn Chanussot, Antonio J. Plaza, Jiawei Zhu, and Bo Li. Pansharpening via detail injection based convolutional neural networks. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 12:1188--1204, 2018. 6,7,2, 3 \[16\]Zi-Rong Jin, Tian-Jing Zhang, Tai-Xiang Jiang, Gemine Vivone, and Liang-Jian Deng. Lagconv: Local context adaptive convolution kernels with global harmonic bias for pansharpening. In AAAI Conference on Artificial Intelligence, 2022. 2, 6, 7, 8, 3 \[17\]Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. CoRR, abs/1412.6980, 2014. 6,1 \[18\]Xiang Li, Wenhai Wang, Xiaolin Hu, and Jian Yang. Selective kernel networks. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 510--519, 2019. 2, 3 \[19\]Giuseppe Masi, Davide Cozzolino, Luisa Verdoliva, and Giuseppe Scarpa. Pansharpening by convolutional neural networks. Remote. Sens., 8:594, 2016. 6, 7, 2, 3 \[20\] Xiangchao Meng, Huanfeng Shen, Huifang Li, Liangpei Zhang, and Randi Fu. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis: Practical discussion and challenges. Inf. Fusion, 46:102--113, 2019. 1 \[21\]Frosti Palsson, Johannes R. Sveinsson, and Magnus Orn Ulfarsson. A new pansharpening algorithm based on total variation. IEEE Geoscience and Remote Sensing Letters, 11:318--322, 2014. 6,7, 2, 3 \[22\]Yaolei Qi, Yuting He, Xiaoming Qi, Yuanyuan Zhang, and Guanyu Yang. Dynamic snake convolution based on topological geometric constraints for tubular structure segmentation. 2023 IEEE/CVF International Conference on Computer Vision (ICCV), pages 6047--6056, 2023. 2 \[23\] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. ArXiv, abs/1505.04597, 2015. 2, 3, 6, 1 \[24\]Wenjie Shu, Hong-Xia Dou, Rui Wen, Xiao Wu, and Liang-Jian Deng. Cmt: Cross modulation transformer with hybrid loss for pansharpening. IEEE Geoscience and Remote Sensing Letters, 21:1-5, 2024. 6,7,2, 3 \[25\]Hang Su, V. Jampani, Deqing Sun, Orazio Gallo, Erik G. Learned-Miller, and Jan Kautz. Pixel-adaptive convolutional neural networks. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 11158--11167, 2019. 2 \[26\]Xin Tian, Yuerong Chen, Changcai Yang, and Jiayi Ma. Variational pansharpening by exploiting cartoon-texture similarities. IEEE Transactions on Geoscience and Remote Sensing, 60:1-16, 2021. 1 \[27\]Xin Tian, Kun Li, Wei Zhang, Zhongyuan Wang, and Jiayi Ma. Interpretable model-driven deep network for hyperspectral, multispectral, and panchromatic image fusion. IEEE Transactions on Neural Networks and Learning Systems, 35:14382--14395, 2023. 6,7,2, 3 \[28\]Gemine Vivone. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Transactions on Geoscience and Remote Sensing, 57:6421--6433, 2019. 1 \[29\]Gemine Vivone. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Transactions on Geoscience and Remote Sensing, 57:6421--6433, 2019. 6,7,2, 3 \[30\]Gemine Vivone, Rocco Restaino, and Jocelyn Chanussot. Full scale regression-based injection coefficients for panchromatic sharpening. IEEE Transactions on Image Processing, 27:3418--3431, 2018. 1 \[31\]Gemine Vivone, Rocco Restaino, and Jocelyn Chanussot. Full scale regression-based injection coefficients for panchromatic sharpening. IEEE Transactions on Image Processing, 27:3418--3431, 2018. 6, 7,2,3 \[32\]Gemine Vivone, Rocco Restaino, Mauro Dalla Mura, Giorgio Licciardi, and Jocelyn Chanussot. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geoscience and Remote Sensing Letters, 11:930--934, 2014. 1 \[33\] Lucien Wald. Data fusion. definitions and architectures -- fusion of images of different spatial resolutions. 2002.6 \[34\] Lucien Wald, Thierry Ranchin, and Marc Mangolini. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogrammetric Engineering and Remote Sensing, 63:691--699, 1997. 6 \[35\]Yudong Wang, Liang-Jian Deng, Tian-Jing Zhang, and Xiao Wu. Ssconv: Explicit spectral-to-spatial convolution for pansharpening. Proceedings of the 29th ACM International Conference on Multimedia, 2021.2,3,6,1 \[36\]Xiao Wu, Tingzhu Huang, Liang-Jian Deng, and Tian-Jing Zhang. Dynamic cross feature fusion for remote sensing pansharpening. 2021 IEEE/CVF International Conference on Computer Vision (ICCV), pages 14667--14676, 2021. 6,7,2, 3 \[37\]Zhong-Cheng Wu, Ting-Zhu Huang, Liang-Jian Deng, Jie Huang, Jocelyn Chanussot, and Gemine Vivone. Lrtcfpan: Low-rank tensor completion based framework for pansharpening. IEEE Transactions on Image Processing, 32:1640--1655, 2023. 6,7, 2, 3 \[38\]Junfeng Yang, Xueyang Fu, Yuwen Hu, Yue Huang, Xinghao Ding, and John Paisley. Pannet: A deep network architecture for pan-sharpening. In 2017 IEEE International Conference on Computer Vision (ICCV), pages 1753--1761, 2017. 6,7,2, 3 \[39\]Rui Zhang, Sheng Tang, Yongdong Zhang, Jintao Li, and Shuicheng Yan. Scale-adaptive convolutions for scene parsing. 2017 IEEE International Conference on Computer Vision (ICCV), pages 2050-2058, 2017. 2 \[40\]Jingkai Zhou, V. Jampani, Zhixiong Pi, Qiong Liu, and Ming-Hsuan Yang. Decoupled dynamic filter networks. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 6643--6652, 2021. 2 \[41\]Xizhou Zhu, Han Hu, Stephen Lin, and Jifeng Dai. Deformable convnets v2: More deformable, better results. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 9300--9308, 2018.2,8 ## 附录 补充材料 ### 摘要 本补充材料详细描述了使用 ARConv 模块的实验设置，涵盖了几个关键方面。它包括对数据集组成的概述，然后是训练过程的配置。此外，材料简要介绍了基准方法，并概述了卷积核替换实验的具体细节。最后，提供了进一步的结果比较和可视化以支持研究结果。 ### 6. 实验细节 #### 6.1. 数据集 本研究中使用的实验数据由三种不同的传感器捕获：WorldView3 (WV3)、QuickBird (QB) 和 高分二号 (GF2)。使用降采样过程来模拟和构建我们的数据集，其中包含三个训练集，分别对应三个传感器。每个训练集都配有降分辨率和全分辨率测试集，从而能够全面评估模型在不同图像质量下的表现。训练集由 PAN/LRMS/GT 图像对组成，尺寸分别为 64×64,  64×64×C,  and  64×64×C64\\times64,\\;64\\times64\\times C,\\;{\\mathrm{and}}\\;64\\times64\\times C64×64,64×64×C,and64×64×C。WV3 训练集包含 9,714 对 PAN/LRMS/GT 图像对 (C=8)(\\mathbf{C}=8)(C=8)，QB 训练集包含 17,139 对 (C=4)(\\mathbf{C}=4)(C=4)，GF2 训练集包含 19,809 对 (C=4)(\\mathbf{C}=4)(C=4)。对应的降分辨率测试集各包含 20 对 PAN/LRMS/GT 图像对，尺寸分别为 256×256,256×256×C256\\times256,256\\times256\\times C256×256,256×256×C, 和 256×256×C256\\times256\\times C256×256×C。全分辨率数据集包含 20 对 PAN/LRMS 图像对，尺寸为 512×512,512×512×C512\\times512,512\\times512\\times C512×512,512×512×C。这些数据集可通过 PanCollection 存储库 \[8\] 公开获取。 #### 6.2. 训练细节 本节详细描述了我们所有实验的训练细节，重点关注损失函数、优化器、批量大小、训练周期数、探索阶段周期数、卷积核高度和宽度学习范围、初始学习率以及学习率衰减方法等方面。在所有实验中，使用的损失函数是 l1l_{1}l1 损失，优化器是 Adam 优化器 \[17\]，批量大小为 16，初始学习率为 0.0006，学习率每 200 个周期衰减为原来的 0.8 倍，探索阶段为 100 个周期。探索阶段的目的是解决根据学习到的卷积核高度和宽度的平均水平选择卷积核采样点数量所带来的收敛挑战。探索阶段结束后，我们根据得到的结果随机选择一组卷积核采样点组合，并在后续训练过程中保持固定。剩余的配置差异如表 9 所示。 #### 6.3. 基准方法 在主文本中，我们详细比较了提出的方法与几种现有方法。为了便于比较，表 12 简要概述了我们研究中使用的基准方法。该表由一条水平线分为两部分，线上列出的是传统方法，线下列出的是深度学习方法。 #### 6.4. 替换卷积实验 在 FusionNet 中，原始架构由四个标准残差块组成。在 AR-FusionNet 中，我们将中间两个残差块中的卷积层替换为我们提出的 ARConv。这一修改使得网络中总共包含四个 ARConv 层，从而增强了其捕获更复杂特征的能力。类似地，在具有五个标准残差块的 LAGNet 中，我们将第二和第四个块中的卷积层替换为 ARConv。这种策略性布局使我们能够在更深的网络结构中评估 ARConv，从而与其他模型进行比较。ARNet 和 CANNet 的构建方式相似，各自将 U-Net 架构 \[23, 35\] 中的标准卷积模块替换为它们各自提出的卷积模块。具体来说，在 CANNet 中，所有标准卷积都被替换为 ARConv，从而将其转化为 ARNet。这为两种网络之间的比较提供了自然的对比，为不同卷积技术的影响提供了有价值的见解。所有三个实验的训练集都是 WV3，其他训练细节可以在表 8 中找到。 #### 6.5. 更多结果 表 10 和 11 展示了在全分辨率 QB 和 GF2 数据集上的性能基准测试，评估了各种方法的有效性。在这三个指标中，DλD_{\\lambda}Dλ 衡量网络捕获光谱信息的能力，而 DsD_{s}Ds 反映了网络保留空间细节的能力。指标 HQNR=(1−Dλ)(1−Ds)\\mathrm{H Q N R}=(1-D_{\\lambda})(1-D_{s})HQNR=(1−Dλ)(1−Ds) 提供了对网络整体性能的全面评估，被认为是评估全分辨率数据集方法的最关键指标。 表 8. 替换卷积实验的不同配置。前三列代表实验名称、训练周期数和卷积核高度宽度学习范围。后续的 Layer1-10 列代表十个卷积层中每一层的最终采样点数量。 | 实验 | 周期数 | 范围 | Layer1-2 | Layer3-4 | Layer5-6 | Layer7-8 | Layer9-10 | |--------------|-----|------|----------|----------|----------|----------|-----------| | AR-FusionNet | 400 | 1-9 | 3×5,7×7 | 7×3,5×5 | | | | | AR-LAGNet | 220 | 1-9 | 5×3,5×3 | 5×3,7×7 | | | | | AR-CANNet | 600 | 1-18 | 3×3,3×3 | 7×5,3×5 | 3×3,3×3 | 3×3,5×5 | 3×5,3×3 | 表 9. 除第 6.4 节详述的替换卷积实验外，所有实验的不同配置。前三列代表实验名称、训练周期数和卷积核高度宽度学习范围，其中"HWR"代表高度和宽度范围。后续的 Layer1-10 列代表 ARNet 中十个卷积层中每一层的最终采样点数量。前三个实验的名称对应于各自的训练数据集，而所有后续实验都使用 WV3 数据集进行训练。 | 实验 | 周期数 | 范围 | Layer1-2 | Layer3-4 | Layer5-6 | Layer7-8 | Layer9-10 | |------------|-----|------|----------|----------|----------|----------|-----------| | WV3 | 600 | 1-18 | 3×3,3×3 | 7×5,3×5 | 3×3,3×3 | 3×3,5×5 | 3×5,3×3 | | QB | 200 | 1-9 | 3×3,3×5 | 5×7,3×3 | 5×3,3×3 | 3×3,7×7 | 3×3,3×3 | | GF2 | 630 | 1-18 | 3×3,3×3 | 3×7,3×5 | 3×3,3×3 | 3×3,5×3 | 3×3,3×3 | | 消融实验 (a) | 600 | 3-3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | | 消融实验 (b) | 600 | 1-18 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | | 消融实验 (c) | 600 | 1-18 | 3×3,3×3 | 5×5,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | | HWR1-3 | 600 | 1-3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | | HWR1-9 | 600 | 1-9 | 5×3,3×3 | 3×3,3×3 | 5×3,5×3 | 3×3,3×3 | 5×3,3×3 | | HWR1-18 | 600 | 1-18 | 3×3,3×3 | 7×5,3×5 | 3×3,3×3 | 3×3,5×5 | 3×5,3×3 | | HWR1-36 | 600 | 1-36 | 3×3,3×3 | 3×3,3×3 | 3×3,5×5 | 5×3,3×3 | 3×3,3×3 | | HWR1-63 | 600 | 1-63 | 3×3,3×3 | 5×5,5×5 | 5×5,5×5 | 3×5,5×5 | 3×3,3×3 | | 与 DCNv2 比较 | 600 | 1-18 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 3×3,3×3 | 表 10. 使用 20 个全分辨率样本在 QB 数据集上的性能基准测试。最佳结果以粗体突出显示，次优结果以下划线表示。 |-------------------|---------------------------|--------------------|--------------| | 方法 | $D_{\\lambda}\\downarrow$ | $D_{s}\\downarrow$ | HQNR↑ | | EXP \[1\] | 0.0436±0.0089 | 0.1502±0.0167 | 0.813±0.020 | | TV \[21\] | 0.0465±0.0146 | 0.1500±0.0238 | 0.811±0.034 | | MTF-GLP-FS \[31\] | 0.0550±0.0142 | 0.1009±0.0265 | 0.850±0.037 | | BDSD-PC \[29\] | 0.1975±0.0334 | 0.1636±0.0483 | 0.672±0.058 | | CVPR19 \[12\] | 0.0498±0.0119 | 0.0783±0.0170 | 0.876±0.023 | | LRTCFPan \[37\] | 0.0226±0.0117 | 0.0705±0.0351 | 0.909±0.044 | | PNN \[19\] | 0.0577±0.0110 | 0.0624±0.0239 | 0.844±0.030 | | PanNet \[38\] | 0.0426±0.0112 | 0.1137±0.0323 | 0.849±0.039 | | DiCNN \[15\] | 0.0947±0.0145 | 0.1067±0.0210 | 0.809±0.031 | | FusionNet \[6\] | 0.0572±0.0182 | 0.0522±0.0088 | 0.894±0.021 | | DCFNet \[36\] | 0.0469±0.0150 | 0.1239±0.0269 | 0.835±0.016 | | LAGConv \[16\] | 0.0859±0.0237 | 0.0676±0.0136 | 0.852±0.018 | | HMPNet \[27\] | 0.1832±0.0542 | 0.0793±0.0245 | 0.753±0.065 | | CMT \[24\] | 0.0504±0.0122 | 0.0368±0.0075 | 0.915±0.016 | | CANNet \[9\] | 0.0370±0.0129 | 0.0499±0.0092 | 0.915±0.012 | | Proposed | 0.0384±0.0148 | 0.0396±0.0090 | 0.924±0.0191 | 表 11. 使用 20 个全分辨率样本在 GF2 数据集上的性能基准测试。最佳结果以粗体突出显示，次优结果以下划线表示。 |-------------------|---------------------------|--------------------|-------------| | 方法 | $D_{\\lambda}\\downarrow$ | $D_{s}\\downarrow$ | HQNR↑ | | EXP \[1\] | 0.0180±0.0081 | 0.0957±0.0209 | 0.888±0.023 | | TV \[21\] | 0.0346±0.0137 | 0.1429±0.0282 | 0.828±0.035 | | MTF-GLP-FS \[31\] | 0.0553±0.0430 | 0.1118±0.0226 | 0.839±0.044 | | BDSD-PC \[29\] | 0.0759±0.0301 | 0.1548±0.0280 | 0.781±0.041 | | CVPR19 \[12\] | 0.0307±0.0127 | 0.0622±0.0101 | 0.909±0.017 | | LRTCFPan \[37\] | 0.0325±0.0269 | 0.0896±0.0141 | 0.881±0.023 | | PNN \[19\] | 0.0317±0.0286 | 0.0943±0.0224 | 0.877±0.036 | | PanNet \[38\] | 0.0179±0.0110 | 0.0799±0.0178 | 0.904±0.020 | | DiCNN \[15\] | 0.0369±0.0132 | 0.0992±0.0131 | 0.868±0.016 | | FusionNet \[6\] | 0.0350±0.0124 | 0.1013±0.0134 | 0.867±0.018 | | DCFNet \[36\] | 0.0240±0.0115 | 0.0659±0.0096 | 0.912±0.012 | | LAGConv \[16\] | 0.0284±0.0130 | 0.0792±0.0136 | 0.895±0.020 | | HMPNet \[27\] | 0.0819±0.0499 | 0.1146±0.0126 | 0.813±0.049 | | CMT \[24\] | 0.0225±0.0116 | 0.0433±0.0096 | 0.935±0.014 | | CANNet \[9\] | 0.0194±0.0101 | 0.0630±0.0094 | 0.919±0.011 | | Proposed | 0.0189±0.0097 | 0.0515±0.0099 | 0.931±0.012 | 图 7 到 14 展示了 ARNet 与各种基准方法在 WV3、QB 和 GF2 数据集的降分辨率和全分辨率测试集上的输出对比。此外，还提供了降分辨率数据集输出与地面真值之间的残差图。这些图表强烈证明了我们提出的方法在多个数据集上的鲁棒性。 #### 6.6. 更多可视化 在 ARNet 中，总共有五个 AR-Resblocks，每个包含两个 ARConv 层。为了分析，我们从每个块中选择一个 ARConv，并可视化其学习到的卷积核高度和宽度的热力图。如图 15 到 18 所示的热力图，为了解卷积核形状与特征图中物体尺寸之间的关系提供了有价值的见解。这种适应性突出了我们方法在处理各种物体尺度方面的灵活性，并为我们方法动态适应不同输入特征的有效性提供了令人信服的证据，使其成为需要精确和可扩展特征提取任务的强大工具。 表12. 各种基准方法的简要介绍。 | 方法 | 年份 | 简介 | |-------------------|------|-----------------------------------| | EXP \[1\] | 2002 | 对 MS 图像进行上采样。 | | MTF-GLP-FS \[31\] | 2018 | 专注于基于回归的全色锐化方法，特别是用于在全分辨率下估计注入系数。 | | TV \[21\] | 2014 | 使用全变差来正则化广泛使用的图像形成模型中的不适定问题。 | | BSDS-PC \[29\] | 2019 | 解决了融合超过四个波段的多光谱图像时传统 BDSD 方法的局限性。 | | CVPR2019 \[12\] | 2019 | 提出了一种基于局部梯度约束的新变分全色锐化模型以改进空间保持。 | | LRTCFPan \[37\] | 2023 | 提出了一种新颖的基于低秩张量补全（LRTC）的多光谱全色锐化框架。 | | | | | | PNN \[19\] | 2016 | 为全色锐化调整了一个简单的三层架构。 | | PanNet \[38\] | 2017 | 用于全色锐化的更深 CNN，结合领域特定知识以保留光谱和空间信息。 | | DiCNN \[15\] | 2018 | 提出了一种新的基于细节注入的卷积神经网络框架用于全色锐化。 | | FusionNet \[6\] | 2021 | 引入了将深度卷积神经网络与传统融合方案结合用于全色锐化。 | | DCFNet \[36\] | 2021 | 通过同时考虑高级语义和低级特征来解决单尺度特征融合的局限性。 | | LAGConv \[16\] | 2022 | 采用具有全局谐波偏置的局部上下文自适应卷积核。 | | HMPNet \[27\] | 2023 | 一种用于融合高光谱、多光谱和全色图像的可解释模型驱动深度网络。 | | CMT \[24\] | 2024 | 将信号处理启发的调制技术集成到注意力机制中，以有效融合图像。 | | CANNet \[9\] | 2024 | 结合非局部自相似性来提高遥感图像融合的有效性并减少冗余学习。 | !\[在这里插入图片描述\](https://i-blog.csdnimg.cn/direct/a166a8a3a58a414cb5554f9d6a3b6133.png) 图 7. WV3 全分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。 !\[在这里插入图片描述\](https://i-blog.csdnimg.cn/direct/ce8c722e8b6b4bd58d141bcbdd8cc8d5.png) 图 8. WV3 降分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。 !\[在这里插入图片描述\](https://i-blog.csdnimg.cn/direct/2e7ea3986c474bce8b113edb21753090.png) 图 9. WV3 降分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。 !\[在这里插入图片描述\](https://i-blog.csdnimg.cn/direct/bf1c5580769845908f8f7087a232b07b.png) 图 10. QB 降分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。  图 11. QB 全分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。  图 12. GF2 全分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。  图 13. GF2 降分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。  图 14. GF2 全分辨率数据集上基准方法的定性结果比较。第一行显示 RGB 输出，第二行显示相对于地面真值的残差。请放大查看最佳效果。 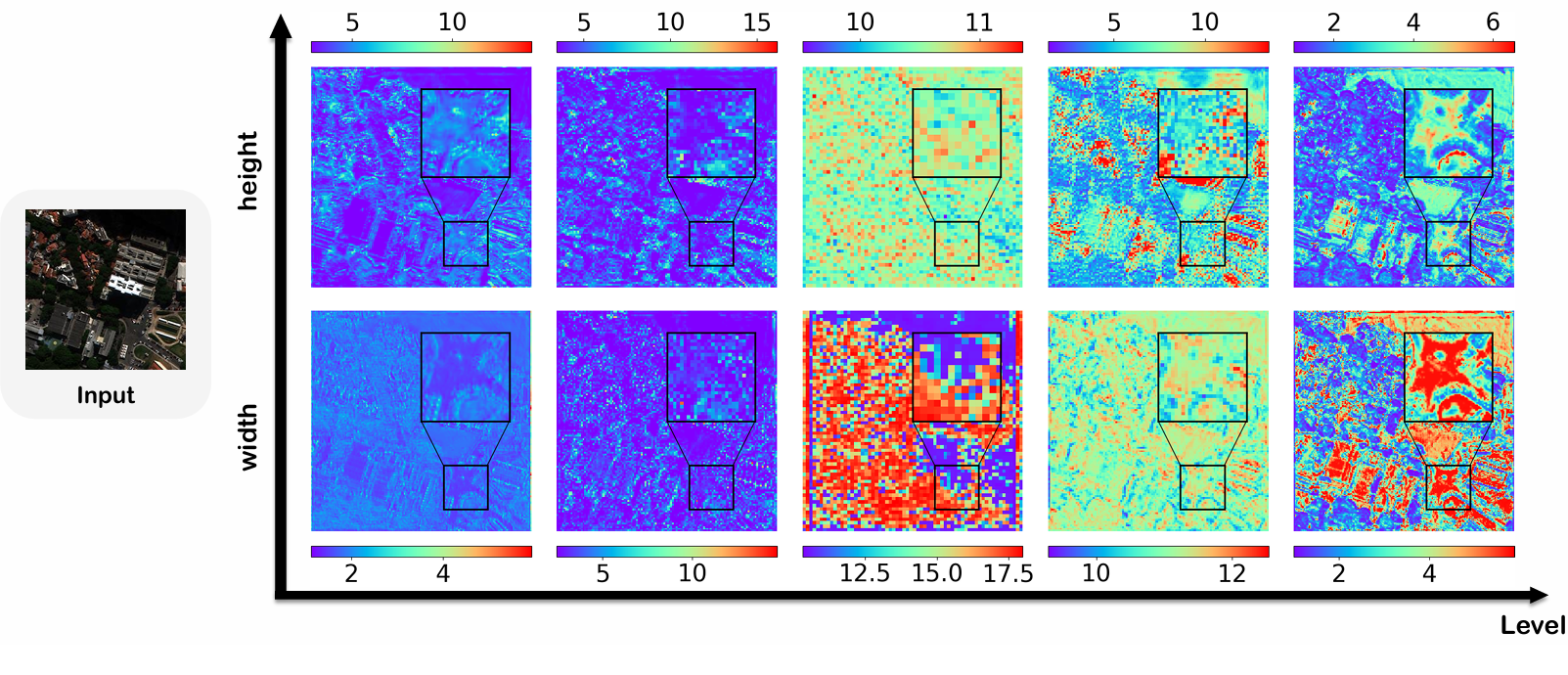 图 15. 不同层卷积核在每个像素处学习到的高度和宽度的热力图。输入图像是来自 WV3 数据集的样本。 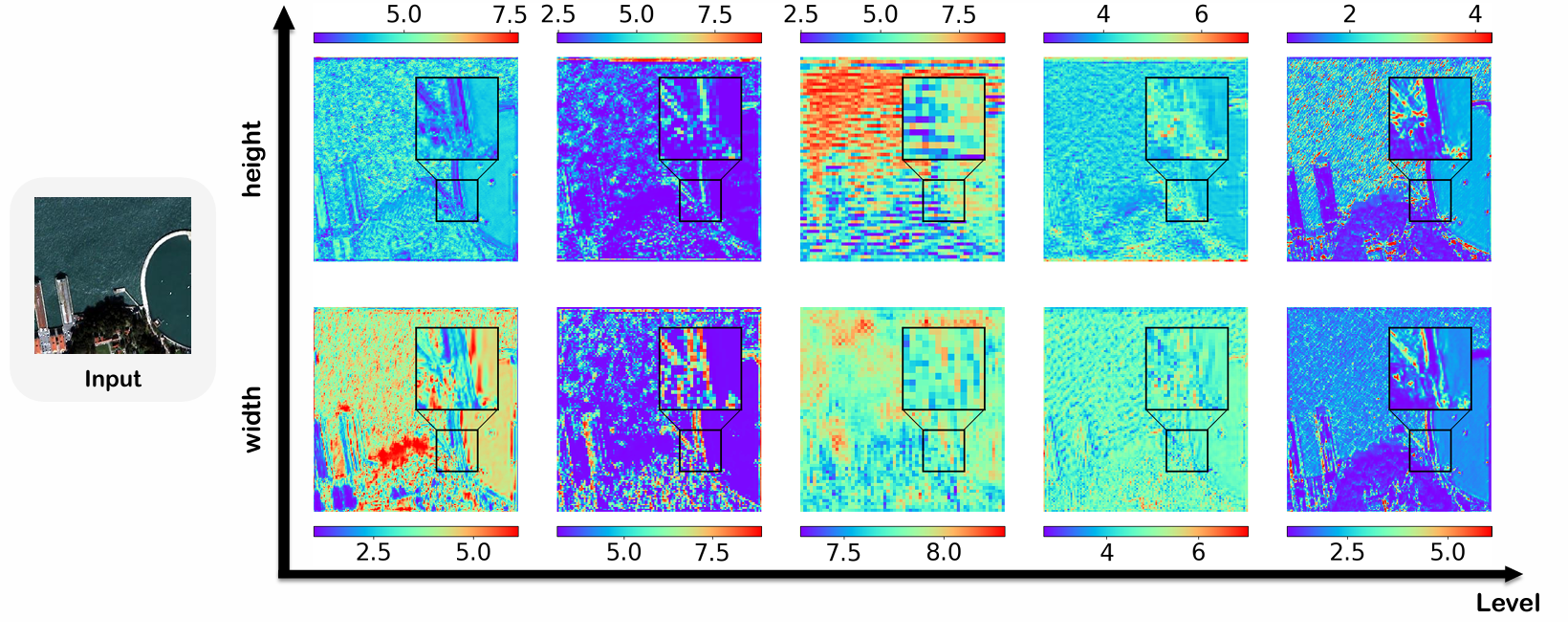 图 16. 不同层卷积核在每个像素处学习到的高度和宽度的热力图。输入图像是来自 QB 数据集的样本。 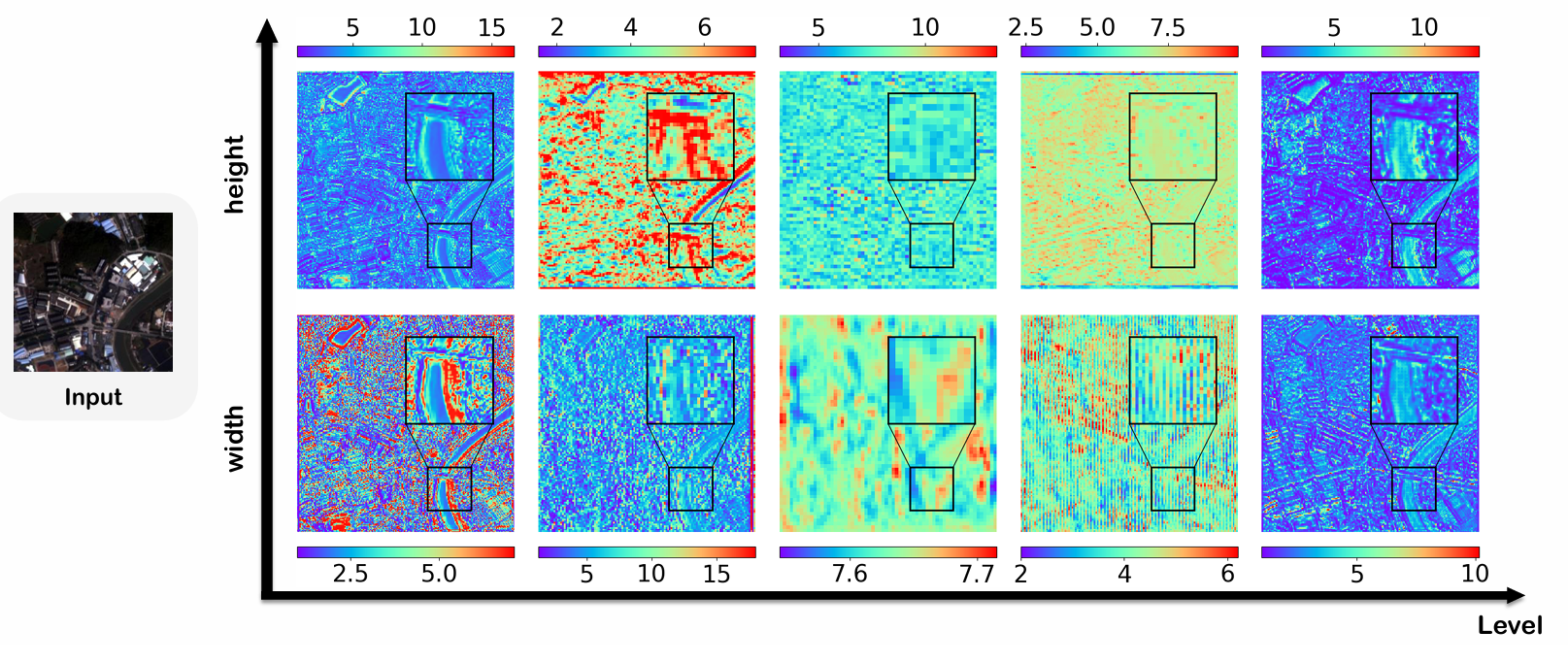 图 17. 不同层卷积核在每个像素处学习到的高度和宽度的热力图。输入图像是来自 GF2 数据集的样本。 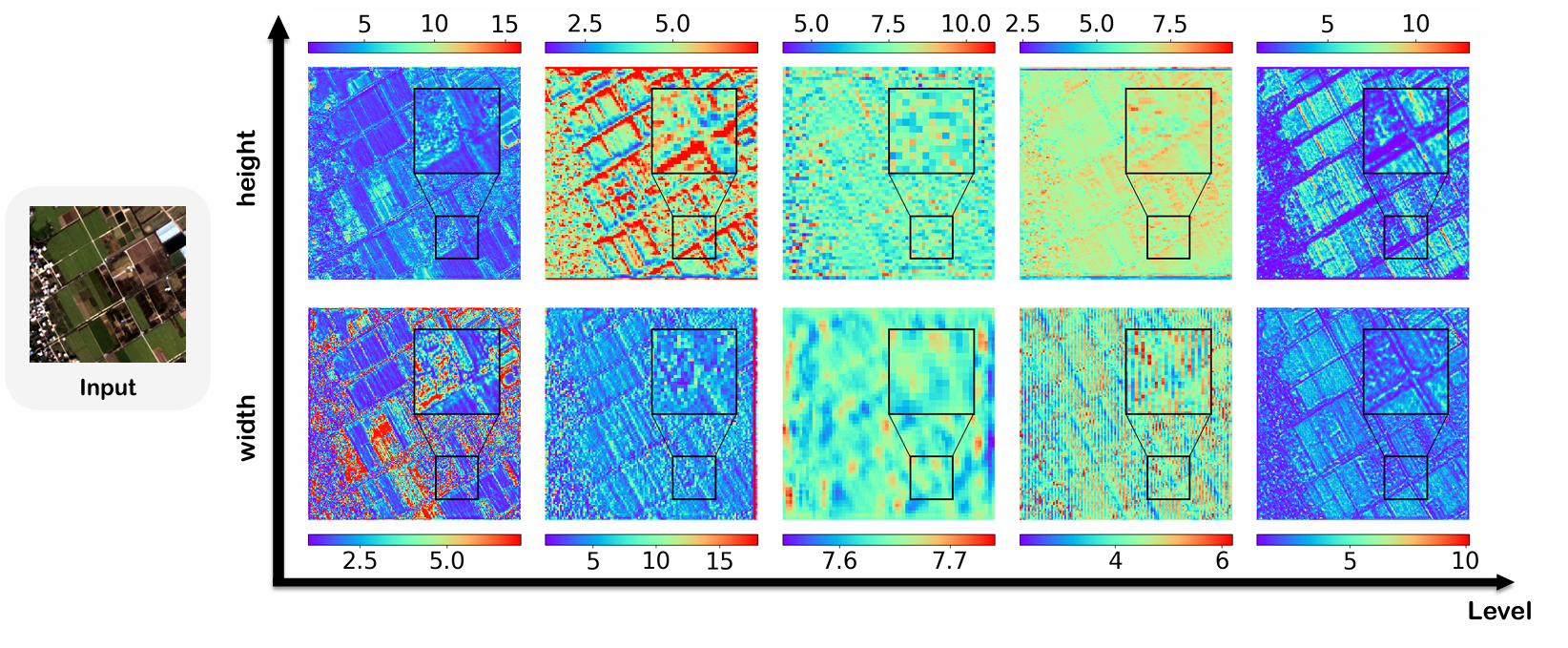 图 18. 不同层卷积核在每个像素处学习到的高度和宽度的热力图。输入图像是来自 GF2 数据集的样本。