【文献阅读】Half-Quadratic Quantization of Large Machine Learning Models

https://dropbox.github.io/hqq_blog/

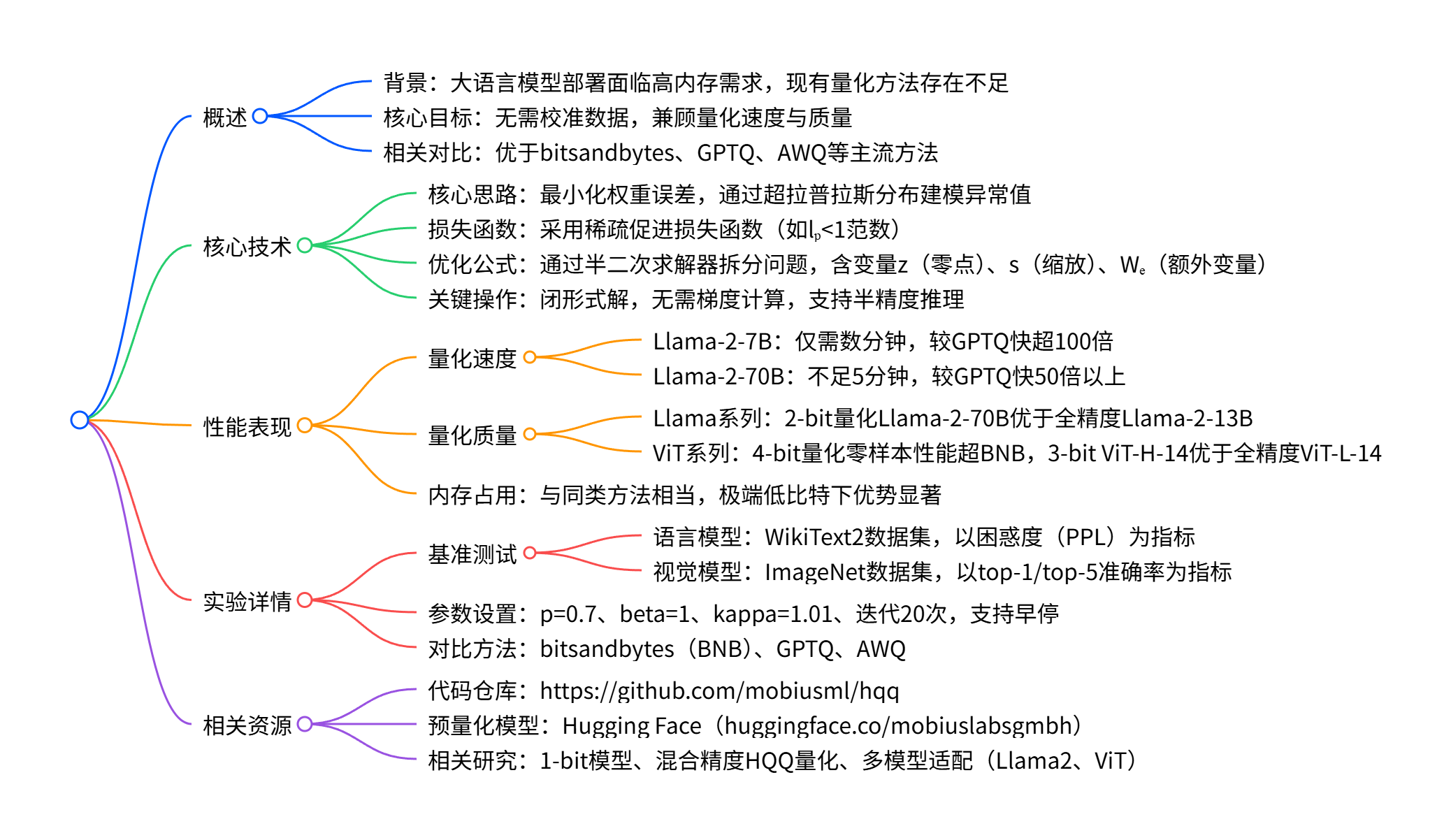
大型机器学习模型的半二次量化（HQQ）

大型语言模型（LLMs）已彻底改变了机器学习的多个子领域，如自然语言处理、语音识别和计算机视觉，使机器能够以前所未有的准确性和流畅度理解并生成输出。然而，部署大型语言模型面临的最关键挑战之一是其高昂的内存需求 ------ 无论是训练阶段还是推理阶段均是如此。bitsandbytes、GPTQ 和 AWQ 等量化方法已实现以显著更低的内存占用运行 Llama-2 等热门大型模型，让机器学习社区能够仅使用单块消费级 GPU 开展卓越的研究工作。

在本文中，我们提出了一种新的量化技术，称为半二次量化（HQQ）。我们的方法无需校准数据，可显著加快大型模型的量化速度，同时提供与基于校准的方法相当的压缩质量。例如，HQQ 处理庞大的 Llama-2-70B 模型仅需不到 5 分钟，较被广泛采用的 GPTQ 快 50 倍以上；在内存占用相当的情况下，2 位量化的 Llama-2-70B 模型通过 HQQ 实现了大幅优于全精度 Llama-2-13B 模型的性能。

支持代码可在 https://github.com/mobiusml/hqq 获取。

引言

模型量化是在有限资源下部署大型模型并节省成本的关键步骤，这对于大型语言模型的训练和推理尤为重要。bitsandbytes 等软件包已实现让消费级 GPU 运行大型模型，这对机器学习社区而言是一项变革性突破。

在仅权重量化领域，主要存在两类方法：一类是无数据校准技术（如 bitsandbytes），仅依赖模型权重而无需外部数据；另一类是基于校准的方法（如 GPTQ 和 AWQ），依赖外部数据集。尽管基于校准的方法量化质量更优，但存在两个主要问题：

校准数据偏差：量化质量会受所提供校准数据的影响而下降；
量化时间：校准过程计算量庞大，对于超大型模型尤为如此，这使得测试和部署多个模型变得困难。

要是能以无校准量化方法的速度达到基于校准方法的量化质量，岂不是很好？这正是我们通过半二次量化（HQQ）方法所实现的目标。

半二次量化

基础量化通常会导致模型精度损失。这是因为这些模型中的权重值范围广泛，在量化过程后可能会发生显著变化。偏离分布的权重（通常称为异常值）是一个特殊的挑战。分组精度调优量化（GPTQ）和激活感知层量化（AWQ）是两类尝试解决该问题的算法，它们依赖校准数据来最小化层输出的误差。

与这些方法不同，我们的方法专门侧重于最小化权重误差而非层激活误差。此外，通过引入稀疏促进损失（如\(l_{p<1}\)范数），我们利用超拉普拉斯分布对异常值进行有效建模 。与平方误差相比，该分布能更准确地捕捉异常值误差的重尾特性，从而更细致地描述误差分布。

我们提出了一种稳健的优化公式来求解量化参数（零点 z 和缩放因子 s）。更具体地说，我们采用稀疏促进损失函数\(\phi()\)（如原始权重 W 与其反量化版本之间的\(l_{F}\)范数）：

这个稀疏促进损失函数的作用，可以通俗理解成 "给权重误差'分优先级'，重点照顾关键少数"：你可以把模型里的权重想象成一堆 "数值物品"------ 大部分是普通、接近的数值（比如都是 1~5 之间），但少数是特别离谱的 "异常值"（比如突然出现 100），这些异常值对模型效果影响还挺大。普通的损失函数（比如平方误差）会 "一视同仁"：不管是普通值还是异常值的误差，都同等较真。但这样容易被异常值的大误差带偏，要么把普通值的量化搞乱，要么异常值的误差没处理好。而 "稀疏促进损失函数"（这里用的\(l_{p<1}\)范数）是专门干 "抓重点" 的：

对大部分普通权重的误差，它 "睁一只眼闭一只眼"（让这些误差尽量 "稀疏"、不用太精细）；
但对那些关键的异常值误差，它会 "盯得很紧"（因为这些异常值对模型效果影响大），逼着量化过程把这些异常值的误差控制得更好。

这么做的好处是：既能快速完成量化（不用在普通权重上花太多精力），又能保住模型精度（把关键异常值的损失降到最低）。

\(\underset{z, s}{argmin} \phi\left(W-Q_{z, s}^{-1}\left(Q_{z, s}(W)\right)\right)\)

其中\(Q_{z, s}()\)是依赖于 z 和 s 参数的量化算子，用于生成量化权重\(W_{q}\)；\(Q_{z, s}()^{-1}\)是反量化算子：\(Q_{z, s}(W)=round(W / s+z)=W_{q}\)\(Q_{z, s}^{-1}\left(W_{q}\right)=s\left(W_{q}-z\right)\)

\(Q_{z,s}(W)\)：用 "打包规则（参数z是打包时的对齐基准，s是压缩比例）" 把物品打包压缩；

\(Q_{z,s}^{-1}(Q_{z,s}(W))\)：把打包好的东西拆出来，恢复成 "打包后再拆开的物品"；

\(W - Q_{z,s}^{-1}(Q_{z,s}(W))\)："原来的物品" 和 "打包拆后物品" 的差距（也就是 "打包造成的损坏 / 变形"）。

而 \(\underset{z,s}{argmin} \phi(\dots)\) 的意思是："找最合适的打包规则（选z和s），让'偏心的检查标准（\(\phi\)，也就是稀疏促进损失函数）'觉得这个'打包损坏'最小"。

第一个公式：\(Q_{z,s}(W) = round(W/s + z) = W_q\)

这里的两个等号是 **"操作定义 + 结果命名"**：

第一个等号 \(Q_{z,s}(W) = round(W/s + z)\)：我们人为规定 "量化操作（Q）" 就是做这三步：先把原物品尺寸（W）除以压缩比例 s，再加对齐基准 z，最后取整（round）。（就像你规定 "打包相机必须先缩 1/20、再对齐格子基准、最后记整数编号"，这是你定的打包规则，不是推导的）
第二个等号 \(round(W/s + z) = W_q\)：我们把 "打包操作的结果（round 后的整数）" 起个名字叫 W_q（量化后的权重）。（就像你把 "相机打包后的格子编号" 叫 "打包编号 W_q"，只是起个名字）

第二个公式：\(Q_{z,s}^{-1}(W_q) = s(W_q - z)\)

这个等号是 **"反量化操作的定义"**------ 因为反量化是量化的 "逆操作"，要把打包步骤反过来：量化的步骤是 "\(W \stackrel{÷s}{\rightarrow} \stackrel{+z}{\rightarrow} \stackrel{round}{\rightarrow} W_q\)"，那逆操作（反量化）就要把步骤倒着做：先抵消 "+z"（减 z），再抵消 "÷s"（乘 s），而 "round（取整）" 是不可逆的（取整会丢小数），所以反量化只能还原到 "取整前的近似值"。

因此我们人为规定 "反量化操作（Q⁻¹）" 就是：用打包编号 W_q 先减 z，再乘 s------ 这是量化步骤的逆运算（除 s 和乘 s 抵消，加 z 和减 z 抵消），所以写成式子就是 \(s(W_q - z)\)。

采用\(l_{p<1}\)范数会使问题变为非凸问题。为求解该问题，我们引入额外变量\(W_{e}\)，采用半二次求解器。这一额外参数能将主问题拆分为更易求解的子问题。此外，为简化问题，我们固定缩放因子 s，仅优化零点 z：\(\underset{z, W_{e}}{argmin} \phi\left(W_{e}\right)+\frac{\beta}{2}\left\| W_{e}-\left(W-Q_{z}^{-1}\left(Q_{z}(W)\right)\right\| _{2}^{2}\right.\)

随后，我们构建子问题并通过交替优化求解：

\(\left(sp_{1}\right) W_{e}^{(t+1)} \leftarrow \underset{W_{e}}{argmin} \phi\left(W_{e}\right)+\frac{\beta^{(t)}}{2}\left\| W_{e}-\left(W-Q_{z}^{-1}\left(Q_{z}(W)\right) \| _{2}^{2}\right.\right.\)

\(\left(sp_{2}\right) z^{(t+1)} \leftarrow argmin \frac{1}{2}\left\| Q_{z}^{-1}\left(Q_{z}(W)\right)-\left(W-W_{e}^{(t+1)}\right)\right\| _{2}^{2}\)\(\beta^{(t+1)} \leftarrow \kappa \beta^{(t)}\)

其中 β 和 κ 为严格正数参数。

为什么要引入额外变量\(W_e\)？------"把'同时干两件事'拆成'分两步干'"

之前的打包难题是：你得同时做两件事：

用 "偏心检查（只较真贵重物品）" 判断打包的损坏程度；
调整打包规则（零点z）让这个损坏尽可能小。

这就像你一边盯着相机有没有摔碎，一边还要手忙脚乱调整打包盒的格子位置 ------ 两件事绑在一起，顾不过来，很容易乱（对应数学里的 "非凸问题"，直接解太复杂）。

引入额外变量\(W_e\)，相当于先 "假装" 一个 "打包损坏情况"（\(W_e\)就是这个 "假装的损坏"），把难题拆成两步：

第一步：先按 "假装的损坏（\(W_e\)）"，调整 "偏心检查" 的标准（让检查更贴合这个假装的情况）；
第二步：再根据调整后的检查标准，微调打包规则（零点z）。

相当于把 "同时盯损坏 + 调打包"，拆成 "先假装损坏→再调打包"，分步骤干就轻松多了（对应把复杂主问题拆成两个好解的子问题）。

额外变量\(W_e\)怎么初始化？------"先随便猜个'初始损坏'，后面慢慢改"

初始化\(W_e\)不用太较真，一般先假设 "打包没怎么损坏"：比如直接把\(W_e\)初始化成 0（相当于刚开始默认 "所有物品打包后都完好无损"）。

这就像你刚开始打包时，先拍胸脯说 "我包得肯定没问题"，后面拆开检查发现有损坏，再慢慢修正这个 "假装的损坏"（更新\(W_e\)）就行 ------ 反正后面会反复调整，初始值不用太精准。

固定缩放因子s，难道要反复实验选s吗？------"s是'大致压缩比例'，不用反复试"

s是 "打包的压缩比例"，不用反复实验选：你可以先看所有物品的尺寸范围（比如模型里权重最小是 1、最大是 100），要塞进 16 个格子（比如 4 位量化），那直接把s设成 "（最大 - 最小）÷ 格子数"（比如\((100-1)÷16≈6\)），先固定这个s。

这就像你打包前先看所有物品的大小，大致定个 "把 100cm 的相机缩成 16 格内的尺寸"，先按这个比例缩，不用试很多比例 ------ 因为后面调z（格子的对齐基准），能微调打包的 "贴合度"，就算s不是最完美，也能通过调z把贵重物品的损坏控住。

子问题\((sp_{1})\)

该问题属于近邻算子形式。当\(\phi()\)为\(l_{1}\)范数时，其解为软阈值算子。对于\(0 ≤p ≤1\)的\(l_{p}\)范数，存在更通用的阈值解，我们采用的是广义软阈值算子：

\(W_{e}^{(t+1)} \leftarrow shrink_{l_{p}}\left(W-Q_{z}^{-1}\left(Q_{z}(W)\right), \beta\right)\)

\(shrink_{l_{p}}(x, \beta)=sign(x) relu\left(|x|-\frac{|x|^{p-1}}{\beta}\right)\)

子问题\((sp_{2})\)

第二个子问题可重写为：

\(z^{(t+1)} \leftarrow \underset{z}{argmin} \frac{1}{2}\left\| z-\left(W_{q}^{(t+1)}-\frac{\left(W-W_{e}^{(t+1)}\right)}{s}\right)\right\| {2}^{2}\)\(W{q}^{(t+1)}=round\left(W / s+z^{(t)}\right)\)

其解为量化分组所沿维度的平均值：\(z^{(t+1)} \leftarrow\left< W_{q}^{(t+1)}-\frac{\left(W-W_{e}^{(t+1)}\right)}{s}\right>\)

在我们的实现中，我们使用缩放因子的倒数\(1/s\)而非 s，因为我们发现这在半精度计算中更稳定。

需注意的是，与基于自动微分（autograd）的梯度下降法不同，我们提出的方法依赖闭形式解，这意味着无需计算梯度。这使得我们能在推理模式下以半精度运行所有计算。此外，求解器仅需几次迭代即可收敛。相比之下，使用 AdamW 优化器和 PyTorch 的自动微分需要数千次迭代才能获得良好结果，且在\(p<1\)（我们实际用于促进稀疏性的参数）情况下会失效。得益于半二次求解方案，我们的量化方法实现了显著的速度提升（量化 Llama-2-7B 时，较自动微分快 100 倍以上），甚至能在几分钟内处理最大型的模型。

量化时间

我们报告了 Llama-2 系列模型的量化时间。我们发现，GPTQ 和 AWQ 的量化时间在不同机器上差异显著。我们的方法全程在 GPU 上以半精度执行量化，仅在求解器完成后使用 CPU 将数据传输至 GPU。HQQ 量化最大的 Llama-2-70B 模型仅需几分钟，较 GPTQ 快 50 倍以上。

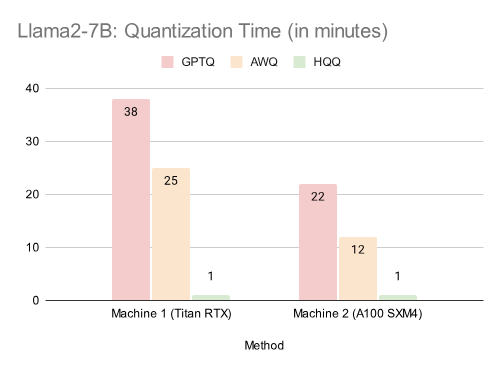
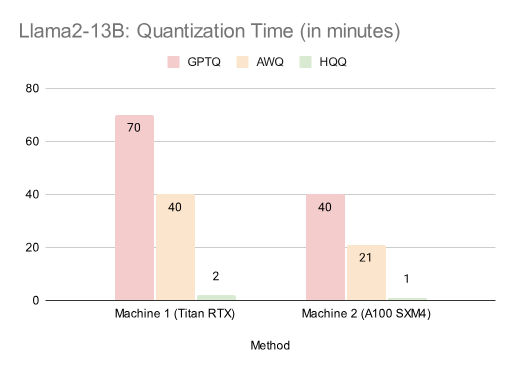
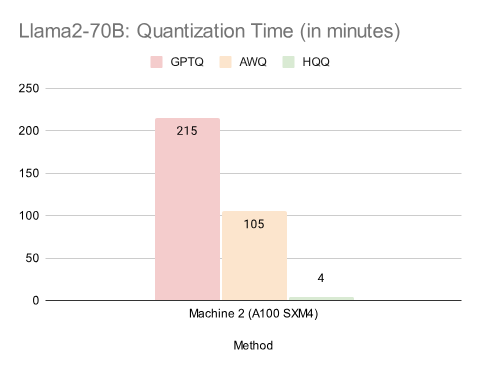
表 1：Llama2-7B：量化时间（单位：分钟）表 2：Llama2-13B：量化时间（单位：分钟）表 3：Llama2-70B：量化时间（单位：分钟）

基准测试

Llama-2 基准测试

为衡量我们方法的量化质量，我们在广泛使用的 wikitext2 数据集上采用困惑度（PPL）指标进行评估。我们还报告了运行量化模型时的 GPU 内存占用（单位：GB，记为 MEM）------ 预测时需额外内存，具体取决于序列长度。我们与社区中广泛使用的主流方法进行对比：BNB（bitsandbytes）、基于 AutoGPTQ 的 GPTQ 以及基于 AutoAWQ 的 AWQ。

关于参数设置，我们固定半二次求解器的参数如下：\(p=0.7\)、beta=1、\(kappa=1.01\)、迭代次数 = 20。此外，我们采用早停策略，当误差不再改善时终止求解器。我们尚未对参数进行大量实验，因此不同的设置可能会带来更优结果。与其他方法类似，我们采用分组策略将权重量化为缓冲区（g128 表示分组大小为 128）。我们还将零点量化为 8 位，且不进行分组或优化。

表 4：Llama-2-7B、Llama-2-13B、Llama-2-70B 模型的量化性能对比（PPL：困惑度，数值越低越好；MEM：GPU 内存占用，单位：GB，数值越低越好）

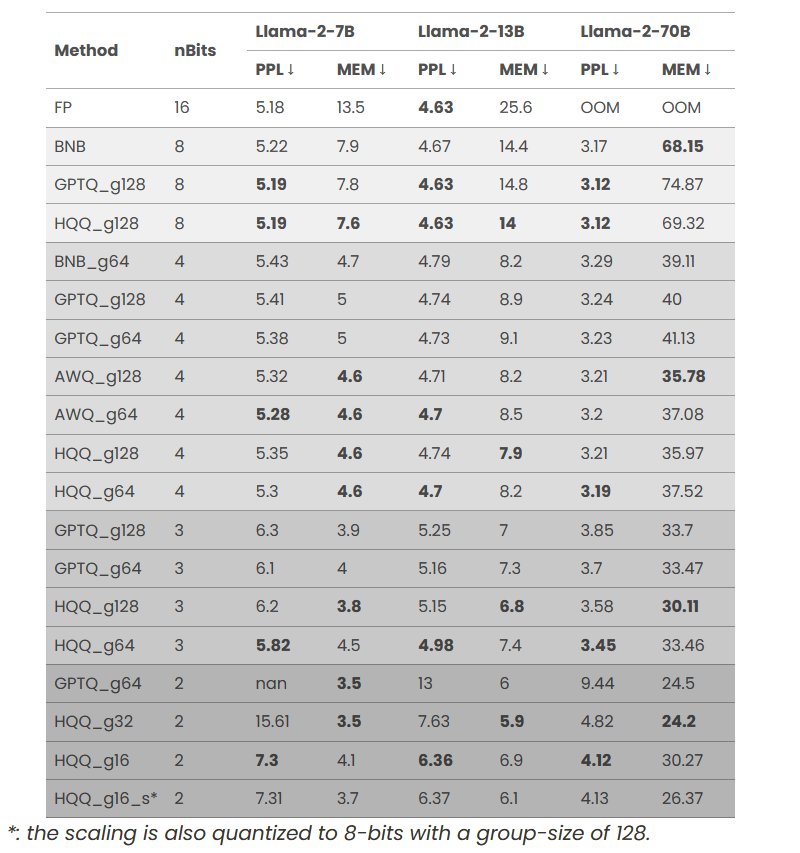
如上表所示，我们的方法在无需校准数据的情况下仍展现出优异性能。将 HQQ 应用于 Llama-2-70B 等大型模型时，2 位量化的 HQQ 模型困惑度低于全精度 Llama-2-13B 模型，且内存占用相当。

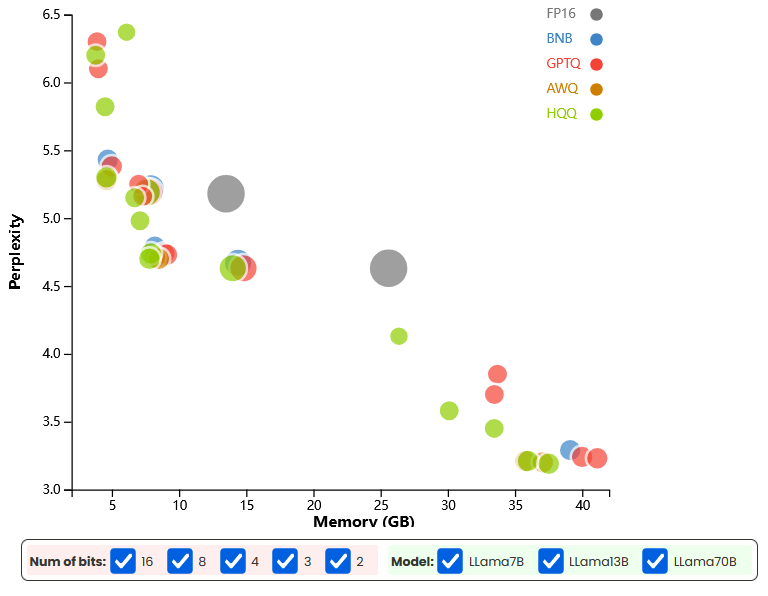
图 1：Llama 系列模型量化性能散点图（横轴：内存占用，单位：GB；纵轴：困惑度；气泡颜色 / 大小对应不同模型和量化位数，悬停或点击气泡可查看详细信息）

ViT 基准测试

我们还在视觉模型上评估了我们量化方法的有效性。具体而言，我们对基于 LAION 数据集训练的视觉 Transformer（ViT）家族中的多个 OpenCLIP 模型进行了量化。由于 Auto-GPTQ 和 Auto-AWQ 的校准仅适用于文本输入，因此我们仅能与 bitsandbytes 进行对比 ------ 将 Transformer 块内的所有线性层替换为其量化版本。

我们进行了两组基准测试，并报告了在 ImageNet 数据集上的 top-1 和 top-5 准确率。第一组基准测试衡量量化模型的零样本性能：我们使用 OpenAI 提示词，通过对所有模板的文本特征求平均来生成零样本分类器。该基准测试直接衡量量化模型的质量，因为评估过程中不涉及任何训练。第二组基准测试将量化模型用作冻结骨干网络，并在其特征之上训练线性 Softmax 分类器，这被称为线性探测（Linear Probing），用于衡量量化模型作为冻结骨干网络的质量。所有结果如下表所示：

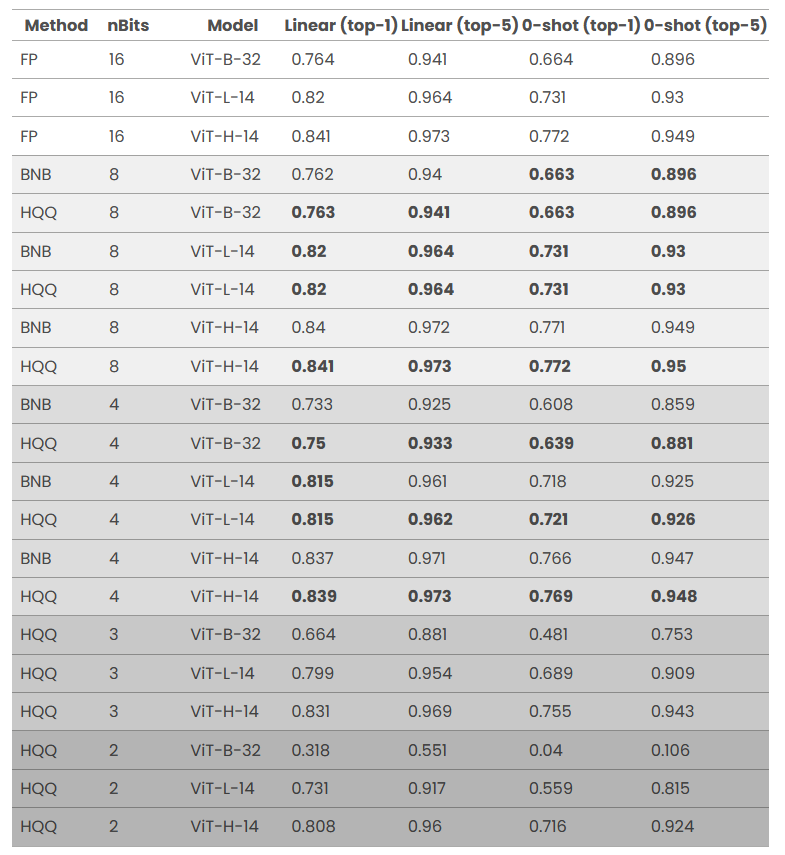
表 5：ViT 系列模型的量化性能对比（指标：线性探测 top-1/top-5 准确率、零样本 top-1/top-5 准确率，数值越高越好）

从结果可以看出，尽管不使用任何校准数据，我们的方法仍能生成高质量的量化模型。在零样本性能上，4 位 HQQ 量化模型大幅优于 4 位 bitsandbytes（BNB）模型（ViT-B-32 的 top-1 准确率提升 3.1%）。在极端低比特量化场景下，3 位量化的 ViT-H-14 模型性能优于全精度 ViT-L-14 模型（零样本 top-1 准确率提升 2.4%），2 位量化版本则大幅优于全精度 ViT-B-32 模型（零样本 top-1 准确率提升 5.2%）。

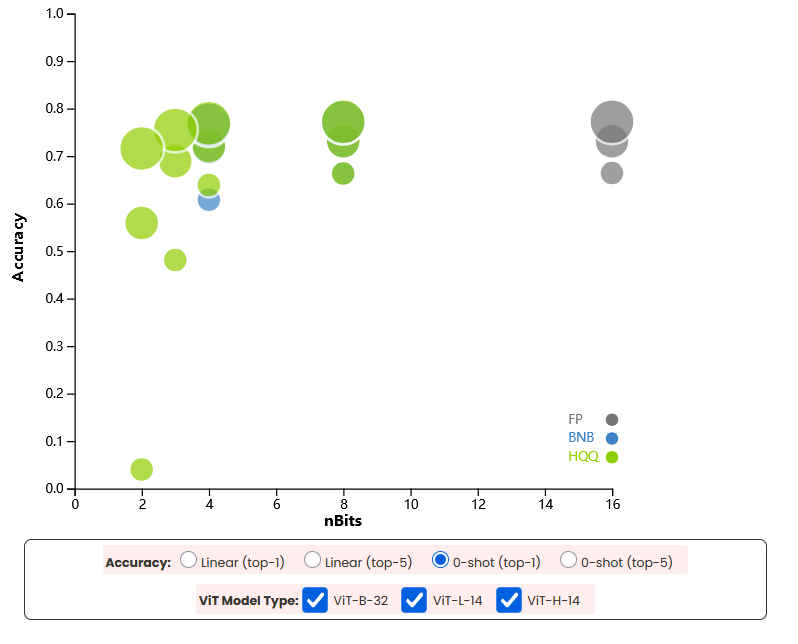
图 2：ViT 系列模型量化性能散点图（横轴：量化位数；纵轴：准确率；气泡颜色 / 大小对应不同模型类型和准确率指标，悬停或点击气泡可查看详细信息）

结论

本文证明，通过我们提出的半二次量化（HQQ）方法，无校准量化能够达到与 GPTQ 和 AWQ 等主流数据依赖型方法相当的量化质量。我们还验证了 HQQ 在不同模型规模和应用场景下，即使在极端低比特量化场景中也具有有效性。此外，借助半二次拆分等高效优化技术，我们的方法将量化时间缩短至几分钟，即使是 Llama-2-70B 等超大型模型也不例外。

我们提供了复现本文所有结果的代码：https://github.com/mobiusml/hqqhttps://github.com/mobiusml/hqq 现成的量化模型可在我们的 Hugging Face 页面获取：https://huggingface.co/mobiuslabsgmbhhttps://huggingface.co/mobiuslabsgmbh

参考文献

@misc{badri2023hqq,title = {Half-Quadratic Quantization of Large Machine Learning Models},url = {https://mobiusml.github.io/hqq_blog/},author = {Hicham Badri and Appu Shaji},month = {November},year = {2023}}