CART是一种构建决策树的经典算法,它能够自动从数据中学习出"if-then"规则,既可以用于分类问题(预测类别),也可以用于回归问题(预测连续值),其核心是通过递归地选择最佳特征和分割点来构建二叉树。
1. CART的本质与特点
1.1. 基本概念
-
Classification And Regression Trees(分类与回归树)
-
由Leo Breiman等人在1984年提出,是决策树算法家族中最经典、最常用的算法之一
-
构建的是二叉树(每个节点最多有两个子节点)
1.2. 核心特点
-
双重用途:同一套算法框架既可处理分类任务,也可处理回归任务
-
二叉树结构:每个节点只进行二分裂(是与否的判断)
-
非参数方法:不对数据分布做任何假设
-
可解释性强:生成的规则易于理解和解释
-
处理混合类型数据:能同时处理数值型和类别型特征
2. CART如何工作?
构建树的三个关键问题:
2.1. 问题1:如何选择最佳分割特征和分割点?
这是CART算法的核心。算法会遍历所有特征和所有可能的分割点,选择使不纯度下降最多的分割方式。
对于分类问题(使用基尼不纯度或熵):
python
# 基尼不纯度公式
Gini(p) = 1 - Σ(p_i)² # p_i是每个类别的比例
# 信息增益(基于熵)
Entropy(p) = -Σ(p_i * log₂(p_i))对于回归问题(使用方差减少):
python
# 选择使子节点方差和最小的分割
MSE = Σ(y_i - y_mean)² / n2.2. 问题2:什么时候停止分裂?
停止条件(预剪枝策略):
-
节点中的样本数少于最小阈值
-
树的深度达到最大限制
-
不纯度下降小于某个阈值
-
所有特征都已使用或没有更多有效分割
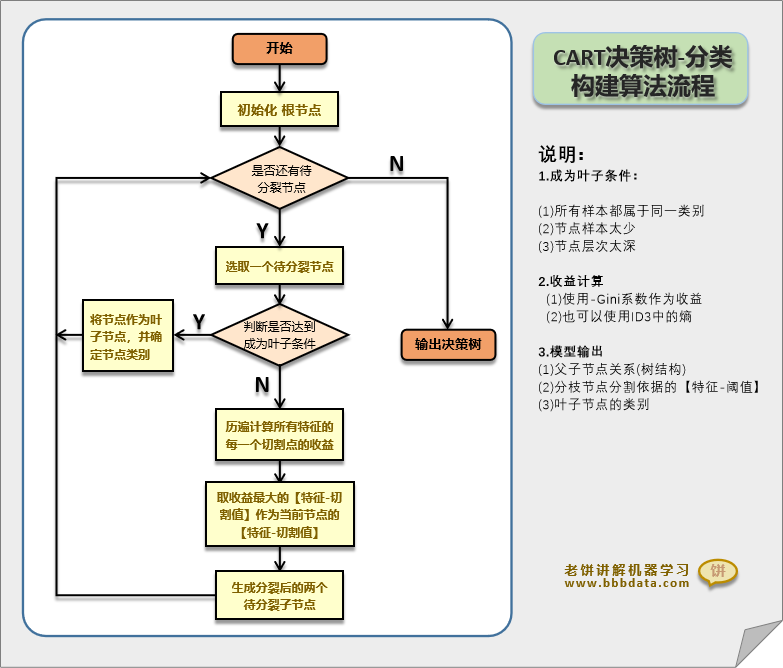
2.3. 问题3:如何确定叶节点的值?
-
分类树:叶节点取该节点中多数类
-
回归树:叶节点取该节点中所有样本的目标值均值
3. CART vs. 其他决策树算法
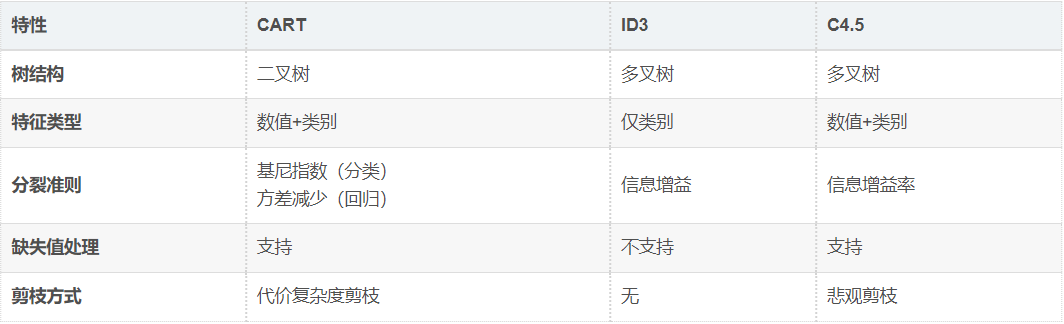
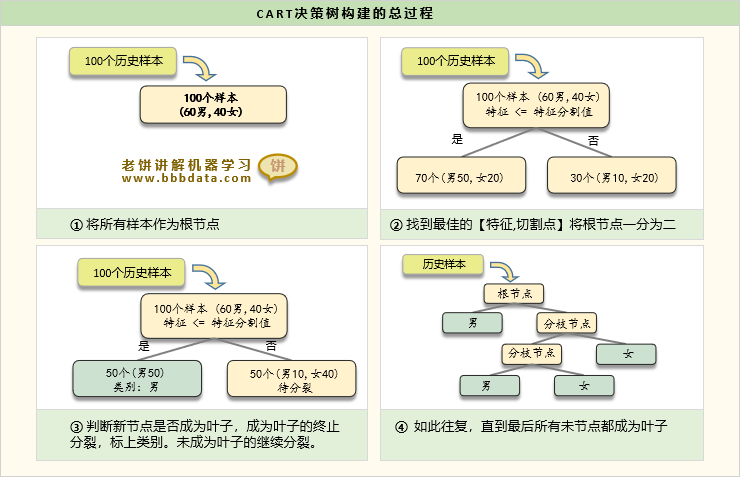
4. 数学原理:以分类树为例
基尼指数计算示例:
假设一个节点有100个样本,其中:
-
类别A:60个
-
类别B:40个
计算基尼不纯度:
python
Gini = 1 - [(60/100)² + (40/100)²]
= 1 - [0.36 + 0.16]
= 1 - 0.52
= 0.48如果按照某个特征分割后:
-
左子节点:70个样本(A:50, B:20),Gini_left = 0.408
-
右子节点:30个样本(A:10, B:20),Gini_right = 0.444
加权基尼指数:
python
Gini_split = (70/100)*0.408 + (30/100)*0.444 = 0.4188基尼指数减少(信息增益):
python
ΔGini = 0.48 - 0.4188 = 0.0612算法会选择使ΔGini最大的特征和分割点。
5. 回归树的特殊处理
回归树预测连续值,其构建过程稍有不同:
python
# 回归树的节点值计算
# 叶节点的预测值 = 该节点所有样本目标值的平均值
# 分割准则:最小化平方误差
For each possible split:
左子节点预测值 = mean(左子节点所有y)
右子节点预测值 = mean(右子节点所有y)
计算两个子节点的MSE(均方误差)之和
选择使MSE和最小的分割6. CART的剪枝策略:代价复杂度剪枝
CART使用后剪枝方法,防止过拟合:
6.1. 代价复杂度公式
python
R_α(T) = R(T) + α|T|
R(T):树T在训练集上的误差
|T|:树的叶节点数量(复杂度)
α:复杂度参数(权衡拟合度与复杂度)6.2. 剪枝过程
-
从完整树T₀开始
-
对每个内部节点,计算剪枝前后的代价复杂度
-
剪掉使R_α减少最多的子树
-
得到一系列嵌套的树{T₀, T₁, ..., T_k}(T_k只剩根节点)
-
通过交叉验证选择最优的α和对应的树
7. CART的优点与缺点
7.1. 优点
-
解释性强:生成的规则像人类思考过程
-
无需数据预处理:对缺失值、异常值相对鲁棒
-
非参数:不对数据分布做假设
-
处理混合特征:数值型、类别型特征都可以
-
特征选择:自动评估特征重要性
-
可视化友好:树结构易于可视化展示
7.2. 缺点
-
不稳定:数据微小变化可能导致完全不同的树
-
容易过拟合:需要仔细剪枝
-
局部最优:贪心算法可能找不到全局最优树
-
不擅长处理线性关系:需要大量分裂来近似线性关系
-
偏向于多值特征:基尼指数更倾向于选择有多个取值的特征
8. 实际应用与代码示例
python
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor, plot_tree
import matplotlib.pyplot as plt
# 1. 分类树示例
from sklearn.model_selection import train_test_split
# 加载鸢尾花数据集
iris = load_iris()
X, y = iris.data, iris.target
# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建CART分类树(使用基尼指数)
clf = DecisionTreeClassifier(
criterion='gini', # 使用基尼指数(默认)
max_depth=3, # 最大深度
min_samples_split=10, # 最小分裂样本数
min_samples_leaf=5, # 叶节点最小样本数
random_state=42
)
# 训练模型
clf.fit(X_train, y_train)
# 预测和评估
accuracy = clf.score(X_test, y_test)
print(f"分类准确率: {accuracy:.2f}")
# 可视化决策树
plt.figure(figsize=(12, 8))
plot_tree(clf,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True,
rounded=True)
plt.title("CART分类树 - 鸢尾花数据集")
plt.show()
# 2. 回归树示例
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
X_reg, y_reg = housing.data[:500], housing.target[:500] # 取前500个样本
# 创建CART回归树
reg = DecisionTreeRegressor(
criterion='squared_error', # 使用均方误差
max_depth=4,
min_samples_split=20,
random_state=42
)
reg.fit(X_reg, y_reg)
print(f"回归树R²分数: {reg.score(X_reg, y_reg):.2f}")
# 特征重要性
import pandas as pd
importance = pd.DataFrame({
'feature': housing.feature_names,
'importance': reg.feature_importances_
}).sort_values('importance', ascending=False)
print("\n特征重要性排序:")
print(importance)关键参数解释:
-
criterion:分裂准则('gini'或'entropy'用于分类,'squared_error'等用于回归)
-
max_depth: 树的最大深度
-
min_samples_split:节点分裂所需的最小样本数
-
min_samples_leaf:叶节点所需的最小样本数
-
max_features:寻找最佳分割时考虑的特征数
9. CART的现代应用
虽然单独的CART树可能不如集成方法强大,但它仍然是许多先进算法的基础:
-
随机森林:由多棵CART树组成
-
梯度提升树:如XGBoost、LightGBM、CatBoost的核心组件
-
孤立森林:用于异常检测
-
特征工程:用于创建交互特征
-
可解释AI:在需要模型解释性的场景中使用
10. 总结
CART算法是决策树家族的经典代表,以其简单性、可解释性和灵活性而闻名。虽然单棵决策树容易过拟合且不稳定,但作为许多集成学习算法的基础构建块,CART在现代机器学习中仍然占有重要地位。
核心价值在于它提供了一种将复杂决策过程可视化和量化的方法,使得非专业人士也能理解模型的决策逻辑。无论是作为独立的可解释模型,还是作为复杂集成模型的组件,CART都展现了其持久的生命力。