大学院-筆記試験練習:线性代数和数据结构(1)
- 1-前言
- 2-线性代数-题目
- 共通問題① 線形代数(大学院入試対策)
-
- 【問題1】一次独立・一次従属
- 【問題2】点と平面
- 【問題3】固有値・固有ベクトルと行列のべき
- [✅ 出題のポイント(学習目的)](#✅ 出題のポイント(学習目的))
- 3-线性代数-参考答案
- 【線形代数】点と平面に関する問題(大学院入試対策)
-
- [(1) 点 A A A を通り,平面 α \alpha α に垂直な直線の方程式](#(1) 点 A A A を通り,平面 α \alpha α に垂直な直線の方程式)
- [(2) 直線と平面の交点および距離 A P AP AP](#(2) 直線と平面の交点および距離 A P AP AP)
- 【結論】
- 4-数据结构-题目
- 5-数据结构-参考答案
- 問1 解法・書写方式
- 問2 解法・書写方式
-
- [(1)O(n log n)・安定](#(1)O(n log n)・安定)
- (2)O(n²)・不安定
- (3)O(n²)・安定
- 問3 解法・書写方式
- [✅ 考试时「照抄模板总结」](#✅ 考试时「照抄模板总结」)
- 6-总结
1-前言
为了升到自己目标的大学院,所作的努力和学习,这里是线性代数和数据结构部分。

2-线性代数-题目
共通問題① 線形代数(大学院入試対策)
以下の問いにすべて答えよ。計算の途中過程も記せ。
【問題1】一次独立・一次従属
次の 3 つのベクトルについて,一次独立か一次従属かを判定せよ。
( 1 0 2 ) , ( 2 1 4 ) , ( − 1 1 − 2 ) \begin{pmatrix} 1\ 0\ 2 \end{pmatrix}, \quad \begin{pmatrix} 2\ 1\ 4 \end{pmatrix}, \quad \begin{pmatrix} -1\ 1\ -2 \end{pmatrix} (1 0 2),(2 1 4),(−1 1 −2)
【問題2】点と平面
点
A ( 2 , − 1 , 3 ) A(2,-1,3) A(2,−1,3)
と,平面
α : ; 2 x − y + 2 z − 5 = 0 \alpha:;2x-y+2z-5=0 α:;2x−y+2z−5=0
が与えられている。
(1)
点 A A A を通り,平面 α \alpha α に垂直な直線の方程式を求めよ。
(2)
その直線と平面 α \alpha α との交点を P P P とするとき,距離 A P AP AP を求めよ。
【問題3】固有値・固有ベクトルと行列のべき
行列
D = ( 4 − 2 1 1 ) D= \begin{pmatrix} 4 & -2\ 1 & 1 \end{pmatrix} D=(4−2 11)
について,以下の問いに答えよ。
(1)
行列 D D D の固有値および固有ベクトルを求めよ。
(2)
D n D^n Dn を求めよ。
✅ 出題のポイント(学習目的)
- 問題1:行列式による一次独立・一次従属の判定
- 問題2 :
法線ベクトル → 垂直直線 → 平面へ代入 → 距離計算 - 問題3 :
固有値 2 つ → 対角化 → 行列のべき D n D^n Dn
3-线性代数-参考答案
【線形代数】点と平面に関する問題(大学院入試対策)
点
A ( 2 , − 1 , 3 ) A(2,-1,3) A(2,−1,3)
および平面
α : ; 2 x − y + 2 z − 5 = 0 \alpha:;2x-y+2z-5=0 α:;2x−y+2z−5=0
が与えられている。以下の問いに答える。
(1) 点 A A A を通り,平面 α \alpha α に垂直な直線の方程式
平面 α \alpha α の法線ベクトルは,方程式の係数より
n ⃗ = ( 2 , − 1 , 2 ) \vec n=(2,-1,2) n =(2,−1,2)
である。
したがって,点 A ( 2 , − 1 , 3 ) A(2,-1,3) A(2,−1,3) を通り,平面 α \alpha α に垂直な直線は,
( x , y , z ) = ( 2 , − 1 , 3 ) + t ( 2 , − 1 , 2 ) (x,y,z)=(2,-1,3)+t(2,-1,2) (x,y,z)=(2,−1,3)+t(2,−1,2)
と表される。
(2) 直線と平面の交点および距離 A P AP AP
直線の式を平面の方程式に代入する。
2 ( 2 + 2 t ) − ( − 1 − t ) + 2 ( 3 + 2 t ) − 5 = 0 2(2+2t)-(-1-t)+2(3+2t)-5=0 2(2+2t)−(−1−t)+2(3+2t)−5=0
整理すると,
4 + 4 t + 1 + t + 6 + 4 t − 5 = 0 4+4t+1+t+6+4t-5=0 4+4t+1+t+6+4t−5=0
6 + 9 t = 0 ⇒ t = − 2 3 6+9t=0 \Rightarrow t=-\frac{2}{3} 6+9t=0⇒t=−32
これを直線の式に代入すると,交点 P P P は
P ( 2 3 , − 1 3 , 5 3 ) P\left(\frac{2}{3},-\frac{1}{3},\frac{5}{3}\right) P(32,−31,35)
である。
次に,距離 A P AP AP を求める。
A P = ∣ t ∣ ⋅ ∣ n ⃗ ∣ = 2 3 2 2 + ( − 1 ) 2 + 2 2 = 2 3 ⋅ 3 = 2 AP=|t|\cdot|\vec n| =\frac{2}{3}\sqrt{2^2+(-1)^2+2^2} =\frac{2}{3}\cdot3 =2 AP=∣t∣⋅∣n ∣=3222+(−1)2+22 =32⋅3=2
【結論】
-
点 A A A を通り平面 α \alpha α に垂直な直線
( x , y , z ) = ( 2 , − 1 , 3 ) + t ( 2 , − 1 , 2 ) (x,y,z)=(2,-1,3)+t(2,-1,2) (x,y,z)=(2,−1,3)+t(2,−1,2) -
交点
P ( 2 3 , − 1 3 , 5 3 ) P\left(\frac{2}{3},-\frac{1}{3},\frac{5}{3}\right) P(32,−31,35) -
距離
A P = 2 AP=2 AP=2
補足(理解のポイント)
- 平面に垂直な直線の方向ベクトルは,平面の法線ベクトルである
- 点から平面までの距離は
A P = ∣ t ∣ ∣ n ⃗ ∣ AP=|t||\vec n| AP=∣t∣∣n ∣
として簡潔に求めることができる
4-数据结构-题目
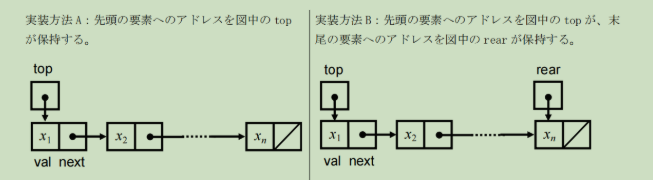
問1
n 個の要素
( x_1, x_2, \ldots, x_n )
からなる連結リストを,以下の実装方法 A や実装方法 B で実現したときの挙動を考える。
以下の問いに答えよ。
実装方法A
先頭の要素へのアドレスを図中の top が保持する。
実装方法B
先頭の要素へのアドレスを図中の top が,
末尾の要素へのアドレスを図中の rear が保持する。
(1)
実装方法Bで実現され,
新たな要素を末尾に追加し,先頭の要素から削除する機能を有する連結リストの分類としてあてはまるものを,
選択肢(a)から 1 つ選び答えよ。
選択肢(a)
- キュー
- スタック
- 単方向連結リスト
- 双方向連結リスト
- 環状(循環)リスト
(2)
実装方法Aと実装方法Bにおける,
末尾の要素を探索するために要する最悪時間計算量を,必要ならば要素数 n を用いて,
オーダー表記でそれぞれ答えよ。
(3)
先頭から順に要素 {7, 5, 3} を格納し,
先頭の要素のアドレスを list1 で保持した線形リストと,
先頭から順に要素 {6, 4} を格納し,
先頭の要素のアドレスを list2 で保持した連結リストが,
図1の擬似コードの関数に与えられたとき,
関数が返す連結リストの要素を先頭から順にすべて答えよ。
なお,与えられたどちらの連結リストも 実装方法A で実現されている。
図1:2つの連結リストに対する擬似コード
text
1: function searchTwoList(list1, list2) {
2: if (list1 == NULL) return list2
3: if (list2 == NULL) return list1
4: if (list1.val >= list2.val) {
5: list1.next = searchTwoList(list1.next, list2)
6: return list1
7: } else {
8: list2.next = searchTwoList(list1, list2.next)
9: return list2
10: }
11: }(4)
実装方法Aで実現され,
先頭の要素のアドレスを list1 と list2 でそれぞれ保持した
2 つの線形リストを,図1の擬似コードの関数を適用したときの
最悪時間計算量を,線形リスト list1 の要素数 n と list2 の要素数 m を用いて,
オーダー表記で答えよ。
問2
ソートする配列の要素数を n とするとき,
以下の(1)から(3)の各条件を満たす ソートアルゴリズムの名前を
選択肢(b)からすべて選び答えよ。
なお,ソートアルゴリズムが 安定 とは,
値が同じ要素が 2 つ以上存在する配列をソートした場合に,
ソートの前後でそれらの要素の順序が変わらないことをさす。
(1)
最悪時間計算量が O(n log n) の 安定なアルゴリズム である。
(2)
最悪時間計算量が O(n²) の 不安定なアルゴリズム である。
(3)
最悪時間計算量が O(n²) の 安定なアルゴリズム である。
選択肢(b)
- バブルソート
- 選択ソート
- 挿入ソート
- ヒープソート
- マージソート
- クイックソート
問3
ハッシュ法(hashing)はデータ探索のアルゴリズムの一種で,
探索対象の n 個の要素
( x_1, x_2, \ldots, x_n )
の値を,ハッシュ関数でデータを記憶するための配列の添字などの値へと写像する。
以下の問いに答えよ。
(1)
データ
( S = {10, 5, 6, 4, 2, 7, 3} )
の先頭の要素から順に,
各要素の値 a を 3 で割った剰余
mod(a, 3) を用いるハッシュ関数を適用するとき,
最初に衝突が起きるのはどの要素の値か答えよ。
(2)
データの要素にハッシュ関数の衝突が起きていない場合の
探索にかかる最悪時間計算量をオーダー表記で答えよ。
5-数据结构-参考答案
問1 解法・書写方式
(1)連結リストの分類
解答例(满分写法)
実装方法Bでは,
要素の追加を末尾で行い,削除を先頭で行うため,
先入先出(FIFO)の構造をもつ キュー に該当する。
よって,① キュー。
(2)末尾要素探索の計算量
解答例
実装方法Aでは末尾への直接参照を持たないため,
先頭から順に探索する必要があり,
最悪時間計算量は O(n) である。
一方,実装方法Bでは末尾要素への参照(rear)を保持しているため,
末尾要素の探索は定数時間で可能であり,
最悪時間計算量は O(1) である。
(3)擬似コードの返す連結リスト
解答例(結果のみ書く)
与えられた擬似コードは,
2 つの降順に整列された連結リストを比較しながら統合する処理である。
よって,返される連結リストの要素は
7 → 6 → 5 → 4 → 3
である。
※ 途中計算は不要(書いても減点されないが時間ロス)
(4)最悪時間計算量
解答例
擬似コードでは,再帰呼び出しのたびに
list1 または list2 のいずれかの要素が 1 つずつ処理される。
よって,全体の比較回数は最大で
list1 の要素数 n と list2 の要素数 m の和に比例し,
最悪時間計算量は O(n + m) である。
問2 解法・書写方式
(※ 理由は不要、番号だけで可)
(1)O(n log n)・安定
解答例
⑤ マージソート
(2)O(n²)・不安定
解答例
② 選択ソート
(3)O(n²)・安定
解答例
① バブルソート,③ 挿入ソート
問3 解法・書写方式
(1)最初に衝突が起きる要素
解答例
各要素に対し mod(a, 3) を適用すると,
10 → 1
5 → 2
6 → 0
4 → 1
となり,値 4 は値 10 と同じ添字に写像される。
よって,最初に衝突が起きる要素は 4 である。
(2)探索の最悪時間計算量
解答例
ハッシュ関数に衝突が発生していない場合,
探索は配列の直接参照により行われるため,
最悪時間計算量は O(1) である。
✅ 考试时「照抄模板总结」
你可以直接记这几句话:
- 「よって,〜である。」
- 「最悪時間計算量は O( ) である。」
- 「〜に該当する。」
- 「直接参照が可能であるため」
6-总结
训练成长。!!