深度神经网络及其问题
深度学习
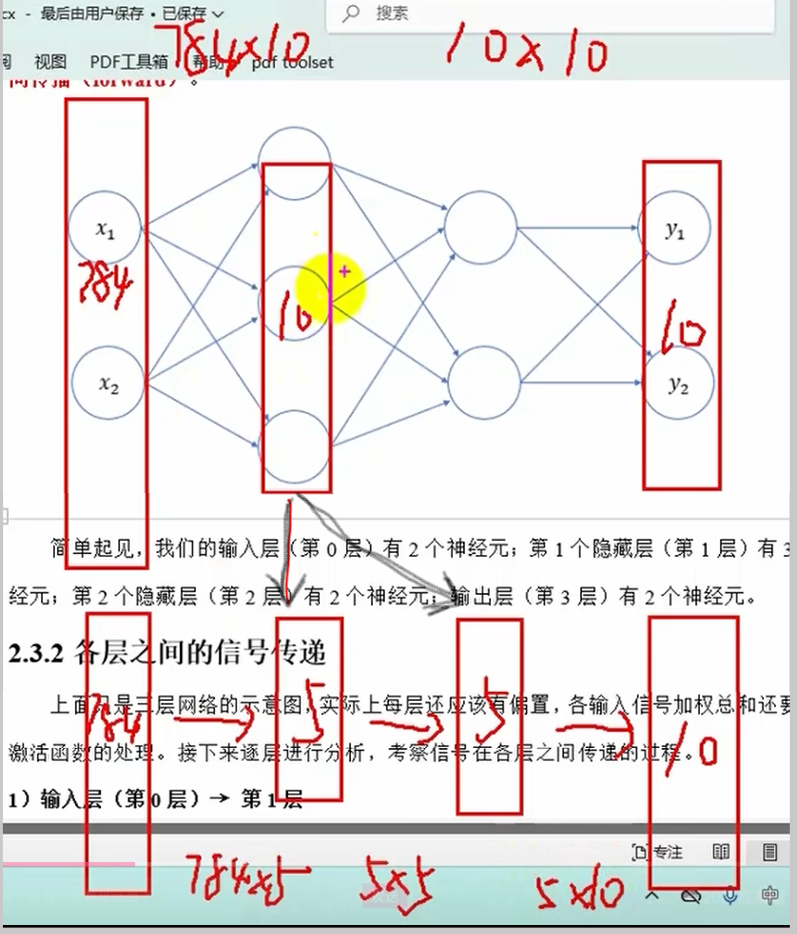
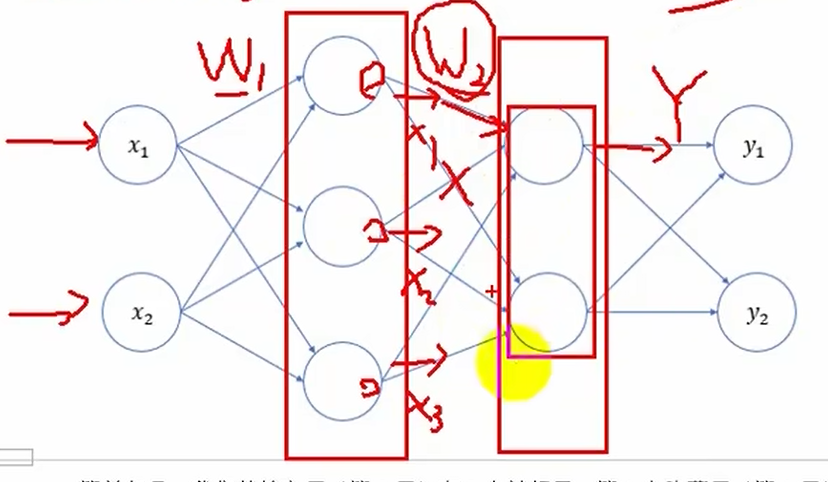
将中间的10个神经元分成两层,每层5个神经元,总参数大大减小

梯度消失和梯度爆炸

更新参数w方法的优化
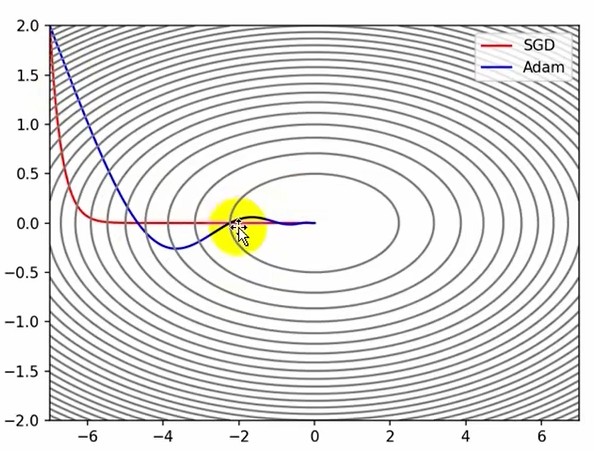
SGD的缺点


# 随机梯度下降SGD
class SGD:
# 初始化
def __init__(self,lr=0.01):
self.lr=lr
# 参数更新w<--w-lr*grads
def update(self,params,grads):
# 遍历传入的所有参数,按照公式更新
for key in params:
params[key]=params[key]-self.lr*grads[key]Momentum(动量法)

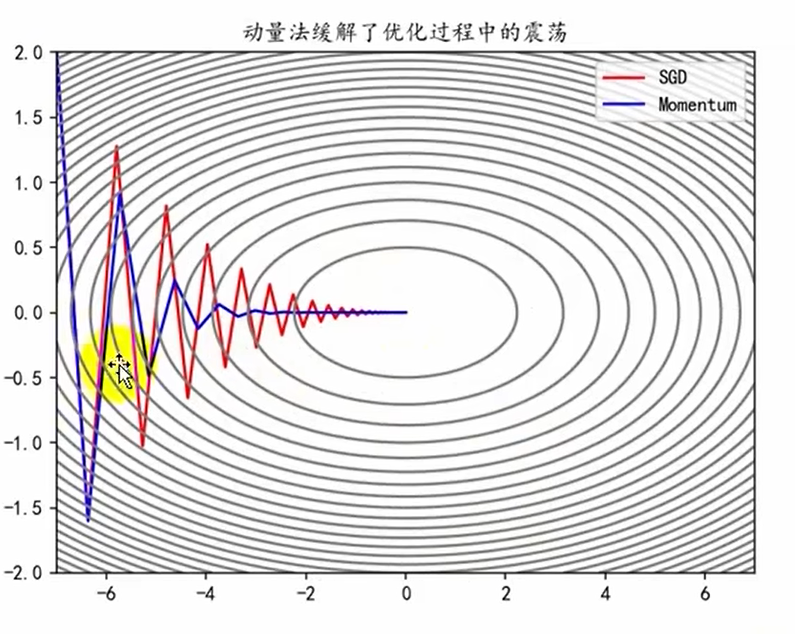
# 动量法Momentum
class Momentum:
def __init__(self,lr=0.01,momentum=0.9):
self.lr=lr
self.momentum=momentum
self.v=None
# 参数更新方法v=momentum*v-lr*grad w=w+v
def update(self,params,grads):
# 对v进行初始化
if self.v==None:
self.v={}
for key,val in params.items():
self.v[key]=np.zeros_like(val)
# 按照公式进行参数更新
for key in params.keys():
self.v[key]=self.momentum*self.v[key]-self.lr*grads[key]
params[key]+=self.v[key]学习率衰减

可以解决动量法找最优解过程中,振幅过大直接冲过最优点太多的问题
等间隔衰减
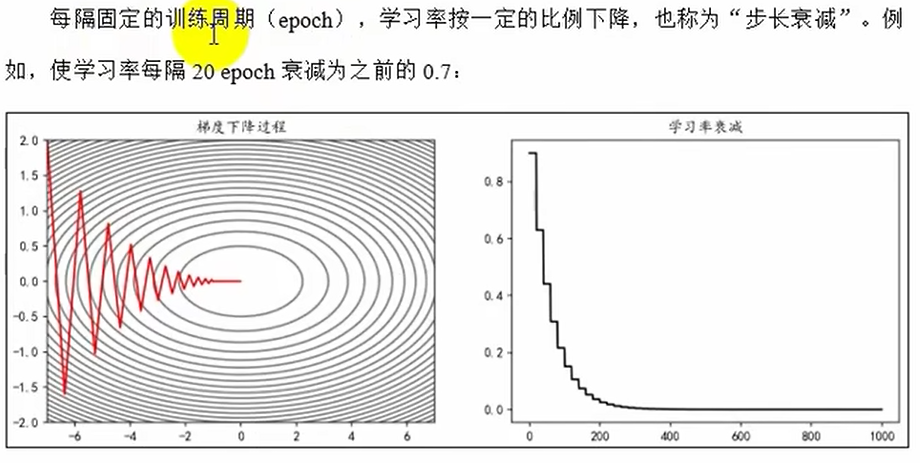
指定间隔衰减
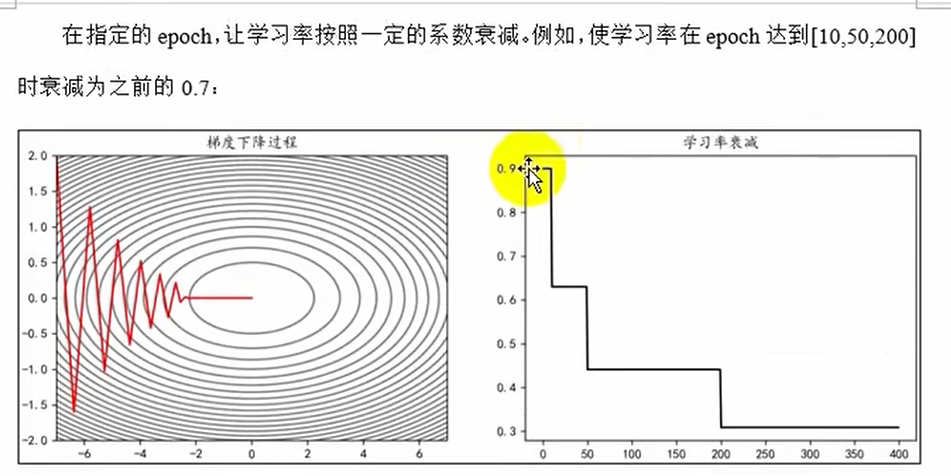
指数衰减
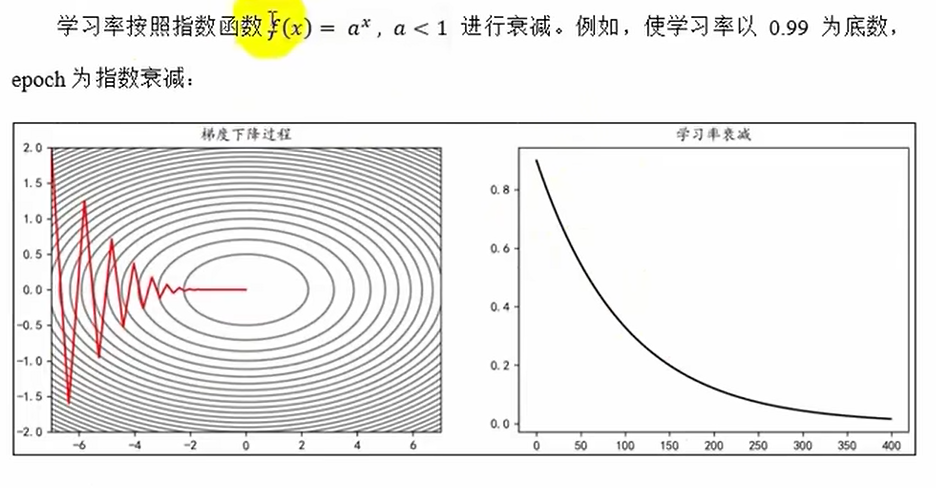
AdaGrad自适应梯度
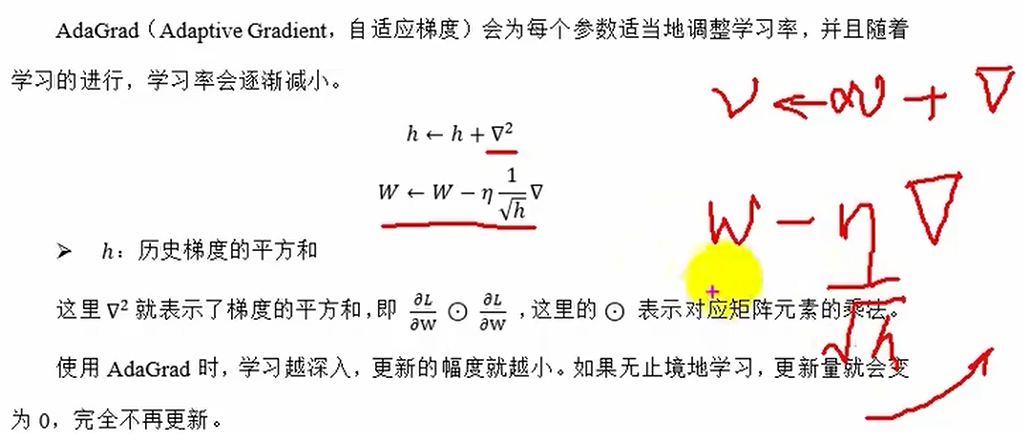
学习率逐渐减小
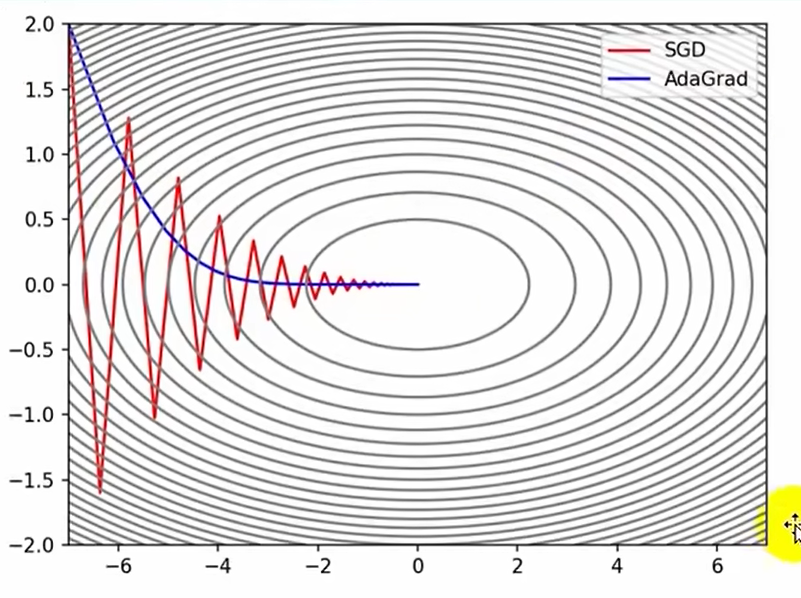
# AdaGrad
class AdaGrad:
# 初始化
def __init__(self,lr=0.01):
self.lr=lr
self.h=None
# 更新方法 h=h+grads^2 w=w-lr*(1/√h ̄)*grads
def update(self,params,grads):
# 对h进行初始化
if self.h==None:
self.h={}
for key,val in params.items():
self.h[key]=np.zeros_like(val)
# 按照公式进行参数更新
for key in params.keys():
self.h[key]+=grads[key]*grads[key]
# 加一个微小量,防止分母为0
params[key]-=self.lr*grads[key]/(np.sqrt(self.h[key])+1e-8)RMSProp均方根传播

αh表示历史梯度占多大比例,(1-α)grads^2表示当前梯度占多大比例
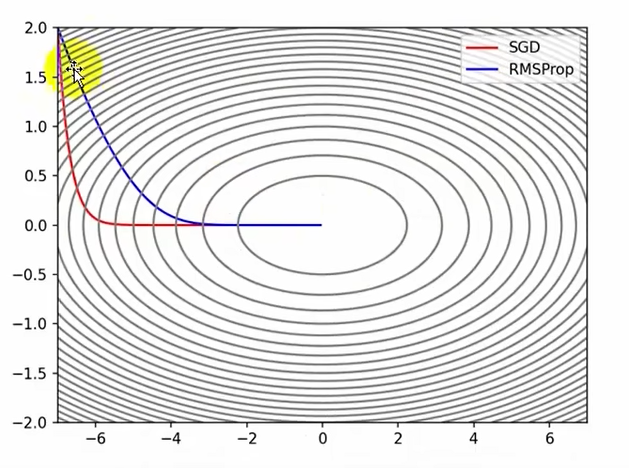
# RMSProp
class RMSProp:
# 初始化 decay-->α
def __init__(self,lr=0.01,decay=0.9):
self.lr=lr
self.h=None
self.decay=decay
# 更新方法 h=decay*h+(1-decay)grads^2 w=w-lr*(1/√h ̄)*grads
def update(self,params,grads):
# 对h进行初始化
if self.h==None:
self.h={}
for key,val in params.items():
self.h[key]=np.zeros_like(val)
# 按照公式进行参数更新
for key in params.keys():
self.h[key]=self.decay*self.h[key]+(1-self.decay)*grads[key]*grads[key]
# 加一个微小量,防止分母为0
params[key]-=self.lr*grads[key]/(np.sqrt(self.h[key])+1e-8)Momentum和( AdaGrad,RMSProp)是两种思路:
Momentum是给梯度一个冲量冲过去那个冲量就是一个加权的历史负梯度
AdaGrad,RMSProp是对学习率进行衰减处理,给学习率添加一个1/根号h
Adam自适应矩估计

v是历史正梯度(包括本次梯度)的累积
h是历史正梯度平方(包括本次梯度)的累积
初始v,h=0都很小,第一次启动v=(1-α1)grads,h=(1-α2)grads**2都很小太慢,
所以给v^=v/1-α1^t,h^=h/1-α2^t,初始启动就很大了
class Adam:
def __init__(self,lr=0.1,alpha1=0.9,alpha2=0.999):
self.lr=lr
self.alpha1=alpha1
self.alpha2=alpha2
self.v=None
self.h=None
self.t=0 # 迭代次数
# 更新方法v=a1*v+(1-a1)*grads h=a2*h+(1-a2)grads**2
# v^=v/(1-a1^t) h^=h/(1-a2^t)
# w=w-lr*v^/√h^ ̄=w-lr_t*v/h ̄
def update(self,params,grads):
# 初始化v和h,这里只判断v就行,因为v的grads为0,则h的grads**2也为0
if self.v==None:
self.v,self.h={},{}
# key一般在神经网络中代表一整层的w or b
for key,val in params.items:
self.v[key]=np.zeros_like(val)
self.h[key]=np.zeros_like(val)
self.t+=1 # 迭代次数加1
# 按照当前的迭代次数改变学习率
lr_t=self.lr*np.sqrt(1-self.alpha2**self.t)/(1-self.alpha1**self.t)
# 遍历所有参数,按公式进行更新
for key in params.keys():
self.v[key]=self.alpha1*self.v[key]+(1-self.alpha1)*grads[key]
self.h[key]=self.alpha2*self.h[key]+(1-self.alpha2)*grads[key]*grads[key]
params[key]-=lr_t*self.v[key]/(np.sqrt(self.h[key])+1e-8)优化方法的综合对比
# 参数w更新--->优化器
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict # 引入有序字典?
from common.optimizer import *
# 定义目标函数:f(w1,w2)--->f(x,y)=1/20x^2+y^2
def f(x,y):
return x**2/20+y**2
# 正常来说(在神经网络),要先进行前向传播得到w,y,J等各种参数
# 再进行反向传播得到dJ/dw求梯度
# 最后带入各种优化器如SGD,Adam等更新梯度
# 但本例直接用上述函数求偏导当梯度向量
def f_grad(x,y):
return x/10,2*y
# 定义初始点位置
init_por=(-7.0,2.0)
# 定义参数和梯度
params={}
grads={}
# 定义优化器,指定学习率
optimizers=OrderedDict()
optimizers['SGD']=SGD(lr=0.1)
optimizers['Momentum']=Momentum(lr=0.1)
optimizers['AdaGrad']=AdaGrad(lr=0.1)
optimizers['Adam']=Adam(lr=0.1)
idx=1 # 子图序号
# 遍历优化器,用优化器更新参数求解最小值点
for key in optimizers:
optimizer=optimizers[key]
# 记录参数点更新的历史
x_history=[]
y_history=[]
# 参数初始化
params['x'],params['y']=init_por[0],init_por[1]
# 指定迭代30次
for i in range(30):
# 保存当前点坐标
x_history.append(params['x'])
y_history.append(params['y'])
# 1.计算梯度
grads['x'],grads['y']=f_grad(params['x'],params['y'])
# 2.更新参数(利用优化器)
optimizer.update(params,grads)
# 画图
x=np.arange(-10,10,0.01)
y=np.arange(-5,5,0.01)
X,Y=np.meshgrid(x,y) # 等高线方法
Z=f(X,Y)
Z[Z>7]=0 # Z高度大于7则不画了
plt.subplot(2,2,idx)
idx+=1
# 绘制等高线
plt.contour(X,Y,Z)
# 画出最小值点
plt.plot(0,0,'+')
# 画出点轨迹曲线
plt.plot(x_history,y_history,'o-',color='red',markersize=2,label=key)
plt.xlim(-10,10)
plt.ylim(-5,5)
plt.legend(loc='best')
plt.show()运行结果:
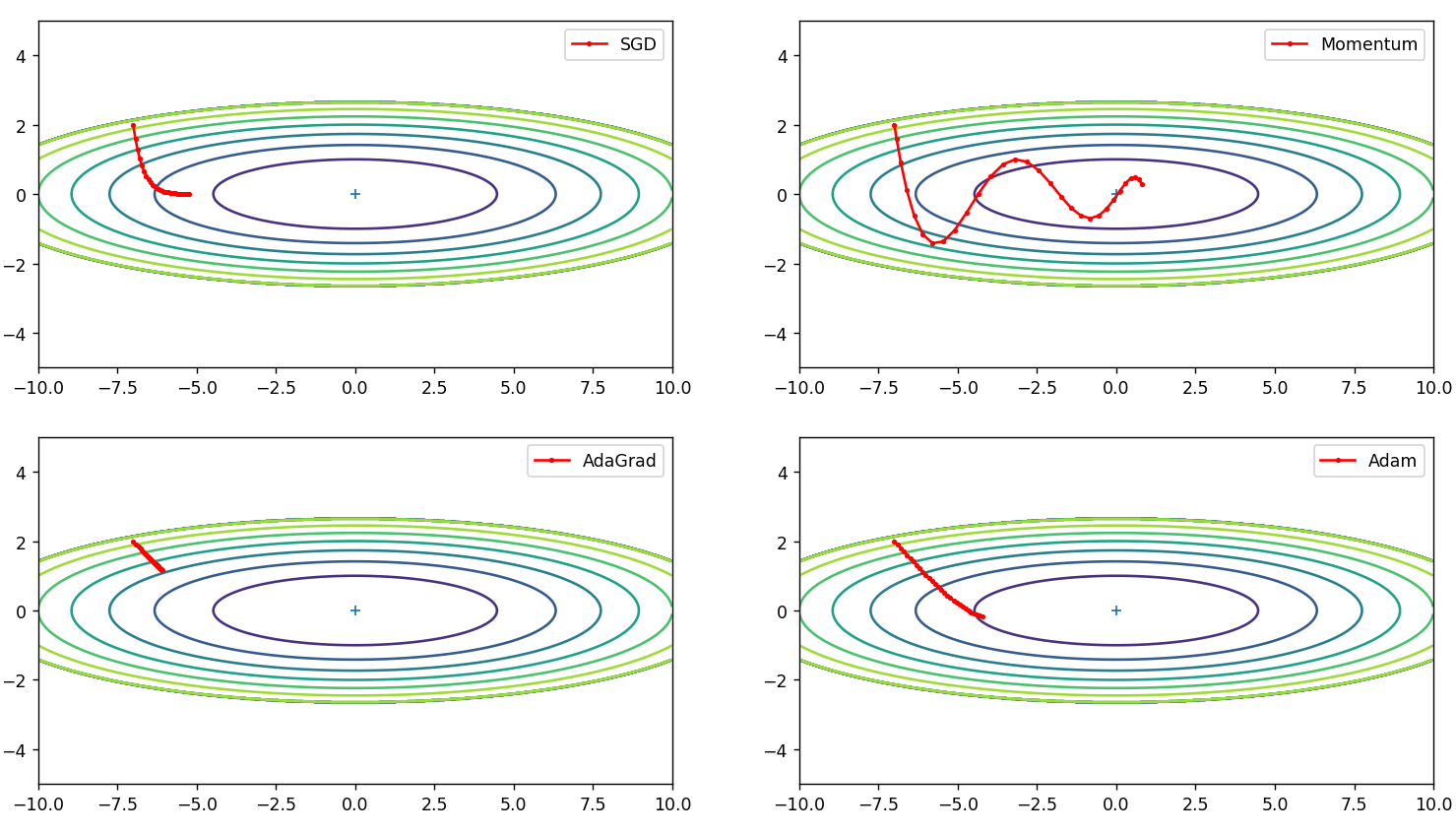
Momentum优化算法加入了历史权重,只用了30次迭代甚至直接冲过了最优解,后面再迭代会冲回来
其他三种方法都因学习率太小迭代次数太少没有找到最优解
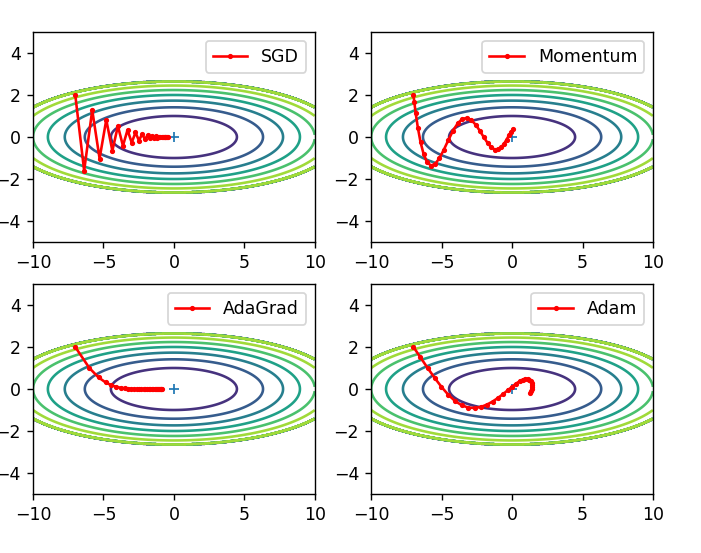
SGD-->0.9
Momentum-->0.08
AdaGrad-->1
Adam-->0.5
参数初始化
参数w一般在Affine(全连接层/仿射层),选择时可以与激活函数的选择结合
常数初始化


秩初始化

正态分布初始化

均匀分布初始化

Xavier初始化(Glorot初始化)

He初始化(Ksiming初始化)

正则化

在机器学习上,对损失函数进行正则化惩罚,来抑制过拟合的可能
Batch Normalization批量标准化

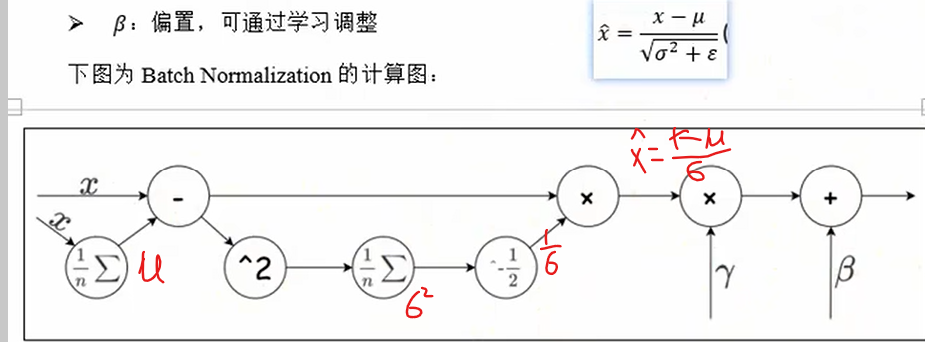
权值衰减

权值方法就类似于机器学习的正则化,是对损失函数进行正则化
Dropout随机失活(隐式集成)

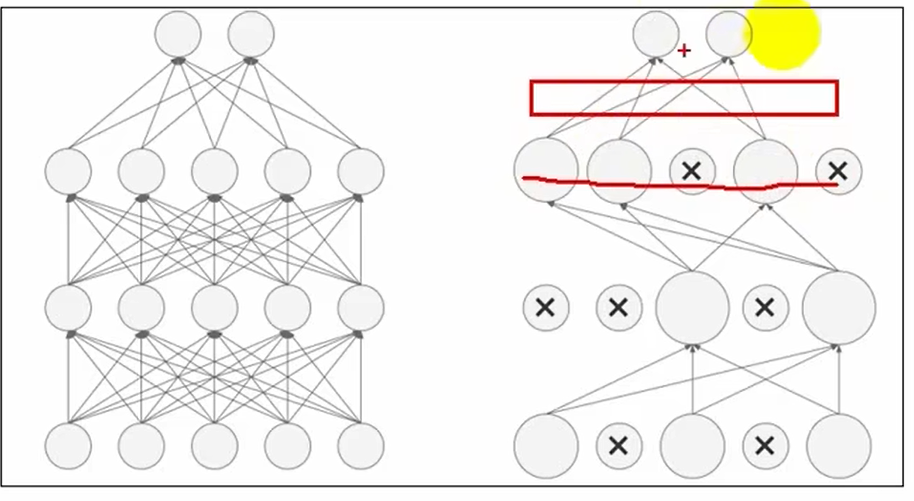
神经元输出值×1/(1-p)是因为关闭输入的神经元会导致输出神经元减小,所以为保证特征一致要进行放大