[机器学习-从入门到入土] 线性回归

[机器学习-从入门到入土] 线性回归

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

• [[机器学习-从入门到入土] 线性回归](#[机器学习-从入门到入土] 线性回归)
• 个人导航
• [线性回归 linear regression](#线性回归 linear regression)
• • • • 基本形式
• 模型表达能力
• • • • 1.特征组合优化（以手机价格预测为例）
      • 2.多项式特征扩展
• 欠拟合与过拟合
• • • • 1.三种拟合状态对比
      • 2.过拟合的权重特征
• 代价函数
• • • • 平方损失函数
      • 梯度下降更新规则
• [L2 正则化（Ridge Regularization）](#L2 正则化（Ridge Regularization）)
• • • • 正则化后的损失函数
      • [λ \lambda λ 的影响](#λ \lambda λ 的影响)
• 含正则化的梯度下降
• • • • 1.偏置项bias更新（不正则化）
      • 2.其他参数weight更新（正则化）
• 正则化的闭式解
• 偏差-方差分解
• 贝叶斯线性回归
• • • • 1.正则化怎么来的
      • 2.OLS只有"一个答案"
      • [2.通过 ln ⁡ λ \ln \lambda lnλ 控制正则化强度](#2.通过 ln ⁡ λ \ln \lambda lnλ 控制正则化强度)
      • 3.数据量对模型参数和预测结果的影响
• 例题

线性回归 linear regression

线性回归用于刻画连续目标变量与输入特征之间的函数关系，其核心假设是：

模型对参数是线性的（linearity in parameters）

基本形式

单变量线性回归模型：
y = w 0 + w 1 x y = w_0 + w_1 x y=w0+w1x

多变量线性回归模型：
y = w 0 + ∑ j = 1 d w j x j = w ⊤ x y = w_0 + \sum_{j=1}^{d} w_j x_j = \mathbf{w}^\top \mathbf{x} y=w0+j=1∑dwjxj=w⊤x

其中：

• w 0 w_0 w0：偏置项（bias）
• w \mathbf{w} w：权重向量
• x \mathbf{x} x：特征向量（含 x 0 = 1 x_0=1 x0=1）

模型表达能力

线性回归的表达能力不取决于是否"线性"拟合数据，而取决于特征设计

1.特征组合优化（以手机价格预测为例）

单独使用高度、宽度：
h ( x ) = w 0 + w 1 ⋅ h e i g h t + w 2 ⋅ w i d t h h(x)=w_0 + w_1 \cdot height + w_2 \cdot width h(x)=w0+w1⋅height+w2⋅width

融合特征（面积）：
h ( x ) = w 0 + w 1 ⋅ ( h e i g h t × w i d t h ) h(x)=w_0 + w_1 \cdot (height \times width) h(x)=w0+w1⋅(height×width)

结论：

合理的特征组合可以显著提升模型表达能力，而不增加模型复杂度

2.多项式特征扩展

通过引入高阶特征，线性模型可拟合非线性关系：
y = w 0 + w 1 x + w 2 x 2 + ⋯ + w n x n y = w_0 + w_1 x + w_2 x^2 + \cdots + w_n x^n y=w0+w1x+w2x2+⋯+wnxn

注意：

• 对 w w w 仍然是线性的
• 对 x x x 是非线性的

欠拟合与过拟合

1.三种拟合状态对比

状态	根本原因	典型表现
欠拟合underfit	模型复杂度过低	高偏差，训练误差大
合适拟合	复杂度匹配数据	泛化性能最佳
过拟合overfit	模型复杂度过高	高方差，测试误差大

原则：在不过拟合的前提下，优先选择更简单的模型

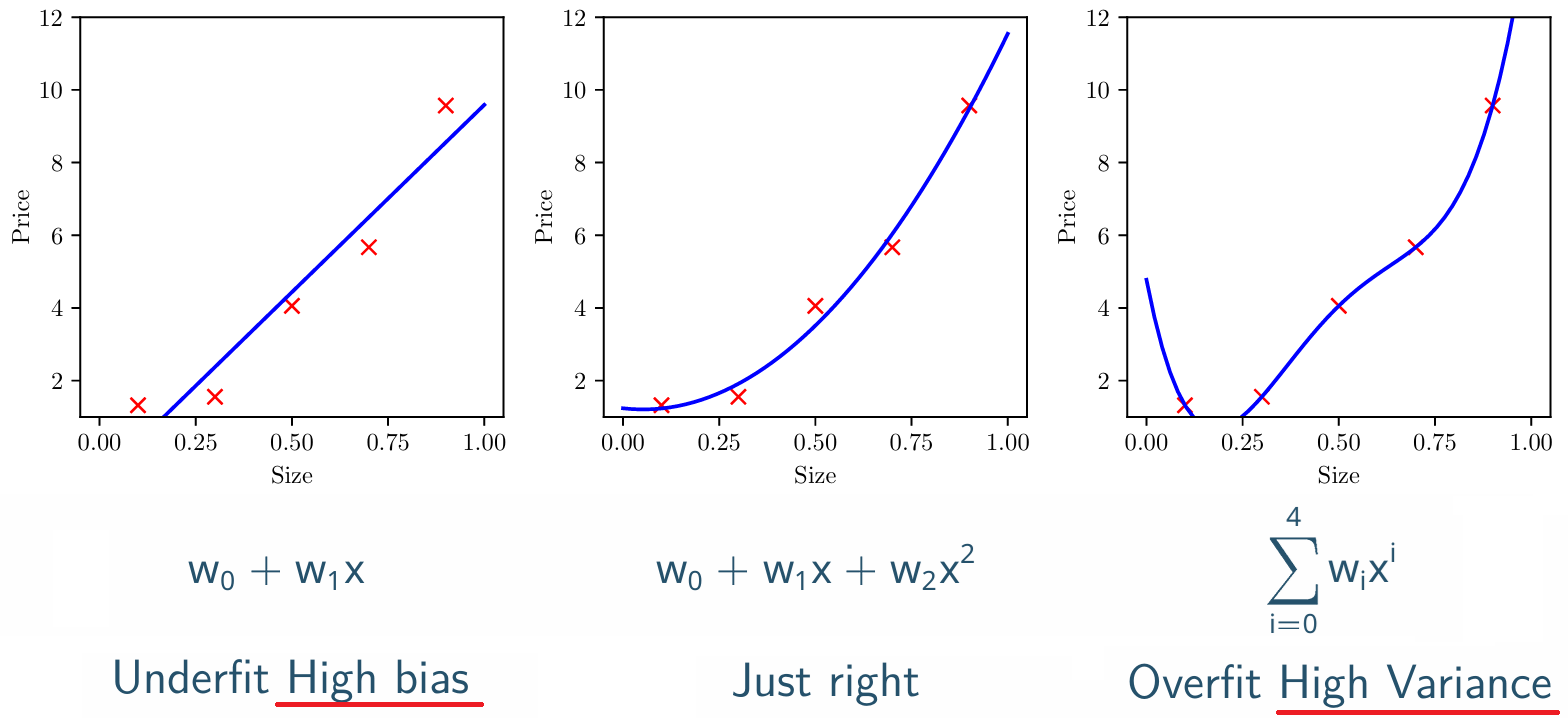
2.过拟合的权重特征

• 权重绝对值异常大
• 高阶项系数正负交替、剧烈振荡

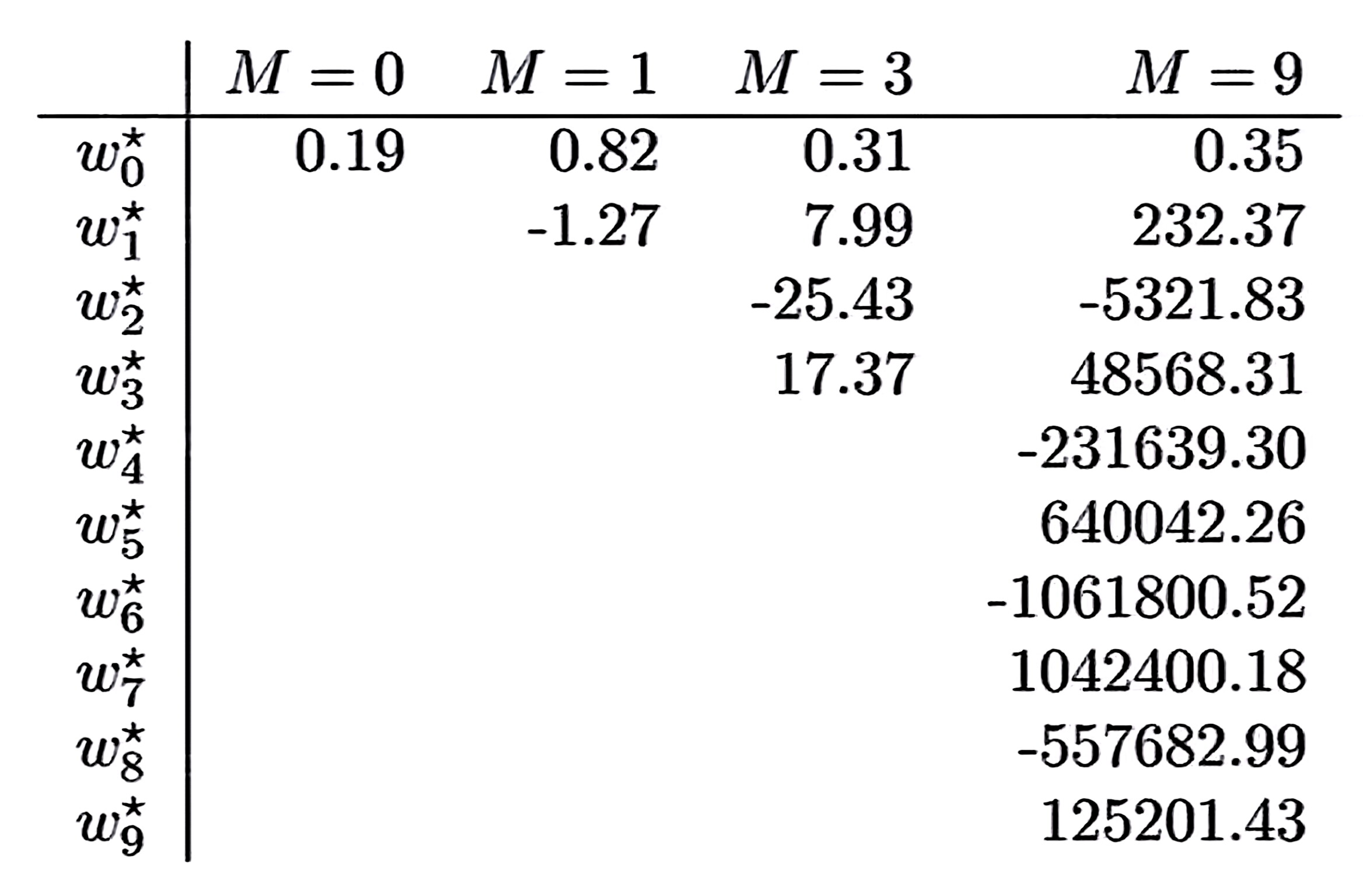
代价函数

平方损失函数

给定训练集 { ( x ( i ) , y ( i ) ) } i = 1 m \{(x^{(i)},y^{(i)})\}{i=1}^m {(x(i),y(i))}i=1m，定义均方误差损失：
J ( w ) = 1 2 m ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) 2 J(w)=\frac{1}{2m}\sum{i=1}^{m}(h_w(x^{(i)})-y^{(i)})^2 J(w)=2m1i=1∑m(hw(x(i))−y(i))2

目标：
min ⁡ w J ( w ) \min_w J(w) wminJ(w)

梯度下降更新规则

w j : = w j − α 1 m ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) x j ( i ) w_j := w_j - \alpha \frac{1}{m}\sum_{i=1}^{m}(h_w(x^{(i)})-y^{(i)})x_j^{(i)} wj:=wj−αm1i=1∑m(hw(x(i))−y(i))xj(i)

L2 正则化（Ridge Regularization）

正则化的基本思想: 加入复杂度惩罚项

正则化后的损失函数

J(w)=\\frac{1}{2m}\\left\[ \\sum_{i=1}^{m}(h_w(x^{(i)})-y^{(i)})^2 * \\lambda \\sum_{j=1}\^{n} w_j\^2 \\right\]

说明：

• w 0 w_0 w0 不参与正则化
• λ \lambda λ 控制惩罚强度

λ \lambda λ 的影响

• λ = 1 \lambda=1 λ=1时：惩罚力度极强，权重参数被强烈压缩，除bias外其余权重趋于0
  -> 模型接近 常数函数
• λ \lambda λ过小时：惩罚力度不足，无法有效限制权重，仍可能发生过拟合
• λ \lambda λ过大时：惩罚过重，权重趋近于0，模型失去拟合能力，导致欠拟合

最优选择：一般希望 λ \lambda λ取较小值，在缓解过拟合的同时，保留模型对数据规律的拟合能力

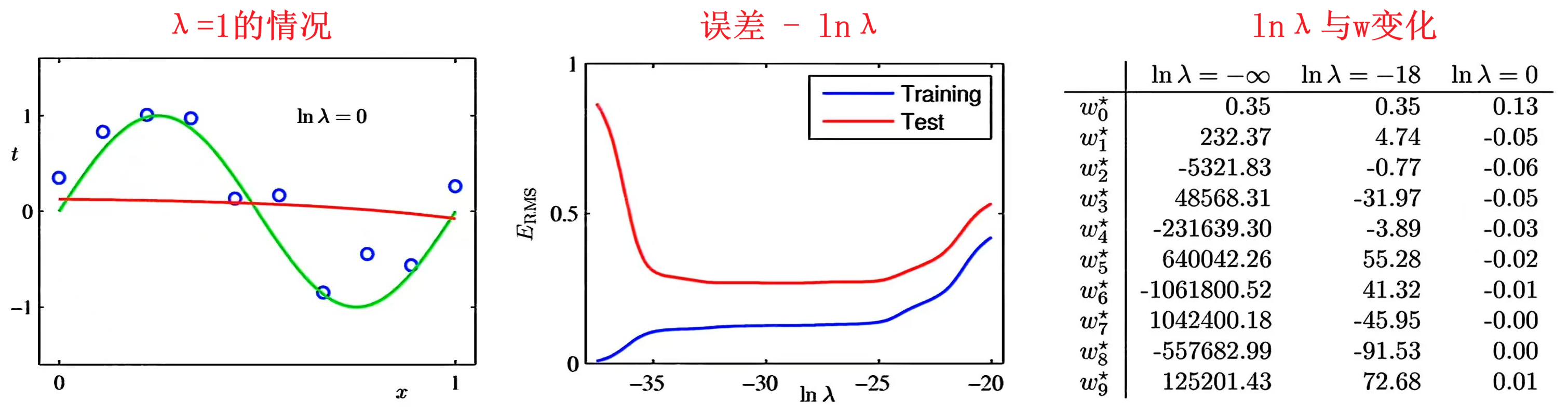
• λ → 0 \lambda \to 0 λ→0：趋近普通最小二乘（易过拟合）
• λ \lambda λ 过大：权重趋近 0（欠拟合）

含正则化的梯度下降

1.偏置项bias更新（不正则化）

w 0 : = w 0 − α 1 m ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) \mathbf{ w_0 := w_0 - \alpha \frac{1}{m} \sum_{i=1}^{m}(h_w(x^{(i)})-y^{(i)}) } w0:=w0−αm1i=1∑m(hw(x(i))−y(i))

2.其他参数weight更新（正则化）

\\mathbf{ w_j := w_j \\left(1-\\alpha\\frac{\\lambda}{m}\\right) * \\alpha \\frac{1}{m} \\sum_{i=1}^{m}(h_w(x^{(i)})-y^{(i)})x_j^{(i)} }

理解：先压缩参数 ( 1 − α λ m ) (1-\alpha\frac{\lambda}{m}) (1−αmλ)，再根据数据更新

正则化的闭式解

无正则化的闭式解: (也是正规方程)
w = ( X ⊤ X ) − 1 X ⊤ y \mathbf{w} = ( X^\top X )^{-1} X^\top y w=(X⊤X)−1X⊤y

矩阵形式解：
w = ( X ⊤ X + λ ⋅ diag ( 0 , 1 , 1 , ... , 1 ) ) − 1 X ⊤ y \mathbf{w} = \left( X^\top X + \lambda \cdot \text{diag}(0,1,1,\dots,1) \right)^{-1} X^\top y w=(X⊤X+λ⋅diag(0,1,1,...,1))−1X⊤y

作用：

• 避免 X ⊤ X X^\top X X⊤X 奇异
• 提升数值稳定性

偏差-方差分解

平方损失下的期望误差：
E [ ( y − y ^ ) 2 ] = ( bias ) 2 + variance + noise \mathbb{E}[(y-\hat{y})^2] = (\text{bias})^2 + \text{variance} + \text{noise} E[(y−y^)2]=(bias)2+variance+noise

• 偏差bias：模型假设带来的系统误差
• 方差variance：对训练数据扰动的敏感度
• 噪声noise：数据本身不可消除误差

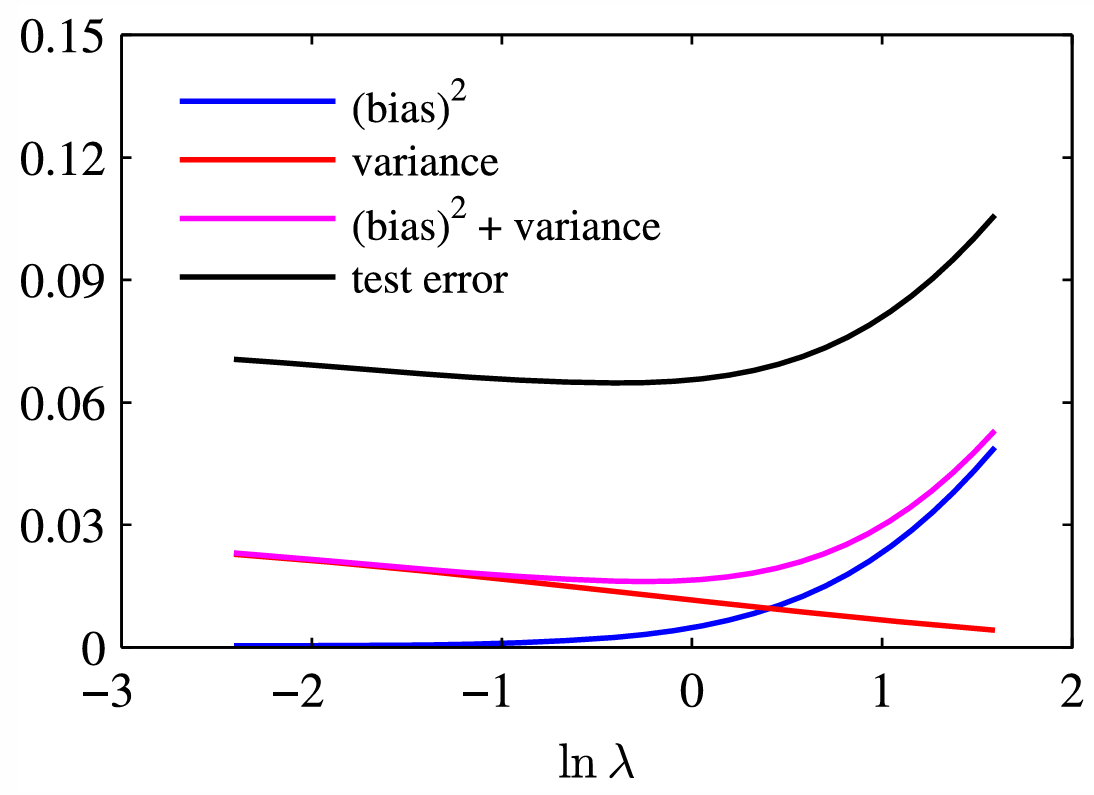
贝叶斯线性回归

前面的内容回答的是：'我该怎么拟合？'
贝叶斯线性回归回答的是：'我凭什么这样拟合？以及我有多确定？'

-> λ 是从哪儿来的？为什么是平方？为什么是 L2，而不是 L1？

频率学派： w w w 是未知但固定的常数, 各参数得到点估计

贝叶斯学派： w w w 是一个随机变量, 每个参数都有一个分布

假设：
t n = w ⊤ φ ( x n ) + ε , ε ∼ N ( 0 , β − 1 ) t_n = w^\top \varphi(x_n) + \varepsilon, \quad \varepsilon \sim \mathcal N(0,\beta^{-1}) tn=w⊤φ(xn)+ε,ε∼N(0,β−1)

于是：
p ( t n ∣ w ) = N ( t n ∣ w ⊤ φ ( x n ) , β − 1 ) p(t_n \mid w) = \mathcal N(t_n \mid w^\top \varphi(x_n), \beta^{-1}) p(tn∣w)=N(tn∣w⊤φ(xn),β−1)

整个数据集（独立同分布）：
p ( t ∣ w ) = ∏ n = 1 N N ( t n ∣ w ⊤ φ ( x n ) , β − 1 ) p(t \mid w) = \prod_{n=1}^N \mathcal N(t_n \mid w^\top \varphi(x_n), \beta^{-1}) p(t∣w)=n=1∏NN(tn∣w⊤φ(xn),β−1)

1.正则化怎么来的

先验: "一开始就相信权重 w w w不应该太大"
p ( w ) = N ( 0 , α − 1 I ) p(w)=\mathcal N(0,\alpha^{-1}I) p(w)=N(0,α−1I)

做 MAP（最大后验）估计 ：
arg ⁡ max ⁡ w p ( w ∣ t ) → max ⁡ w ln ⁡ p ( t ∣ w ) + ln ⁡ p ( w ) \arg\max_w p(w \mid t) \\ \rightarrow \\ \max_w \ln p(t|w) + \ln p(w) argwmaxp(w∣t)→wmaxlnp(t∣w)+lnp(w)

推导得:
ln ⁡ p ( t ∣ w ) + ln ⁡ p ( w ) = − β 2 ∑ n = 1 N ( t n − w ⊤ φ ( x n ) ) 2 − α 2 w ⊤ w + const \ln p(t|w) + \ln p(w) = -\frac{\beta}{2} \sum_{n=1}^N (t_n - w^\top \varphi(x_n))^2 - \frac{\alpha}{2} w^\top w + \text{const} lnp(t∣w)+lnp(w)=−2βn=1∑N(tn−w⊤φ(xn))2−2αw⊤w+const

相当于要最小化:
∑ n = 1 N ( t n − w ⊤ φ ( x n ) ) 2 + α β w ⊤ w → 平方误差 + λ ∥ w ∥ 2 \sum_{n=1}^N (t_n - w^\top \varphi(x_n))^2 + \frac{\alpha}{\beta} w^\top w \\ \rightarrow \\ 平方误差+λ∥w∥^2 n=1∑N(tn−w⊤φ(xn))2+βαw⊤w→平方误差+λ∥w∥2

得到了 λ = α β \lambda = \frac{\alpha}{\beta} λ=βα

• 先验精度 α \alpha α：控制权重偏小的强度
• 数据精度 β \beta β：控制对数据的信任程度

α \alpha α 越大 → 越相信"权重应小"

β \beta β 越大 → 越相信数据

-> L2 正则不是技巧，而是"高斯先验"的必然结果

2.OLS只有"一个答案"

前面所有方法，最后得到的都是 w ^ \hat w w^ 一个解

但不知道：

• 这个解稳不稳？
• 数据少的时候靠不靠谱？
• 哪个预测区间更可信？

贝叶斯给的不是一个点，而是：
p ( w ∣ t ) = N ( m N , S N ) p(w|t)=\mathcal N(m_N,S_N) p(w∣t)=N(mN,SN)

• 每个参数都有 方差
• 预测输出也是一个 分布

-> 可以说："预测 y = 3.2 y=3.2 y=3.2，但 95% 的概率在 [ 2.8 , 3.6 ] [2.8,3.6] [2.8,3.6] 之间"

2.通过 ln ⁡ λ \ln \lambda lnλ 控制正则化强度

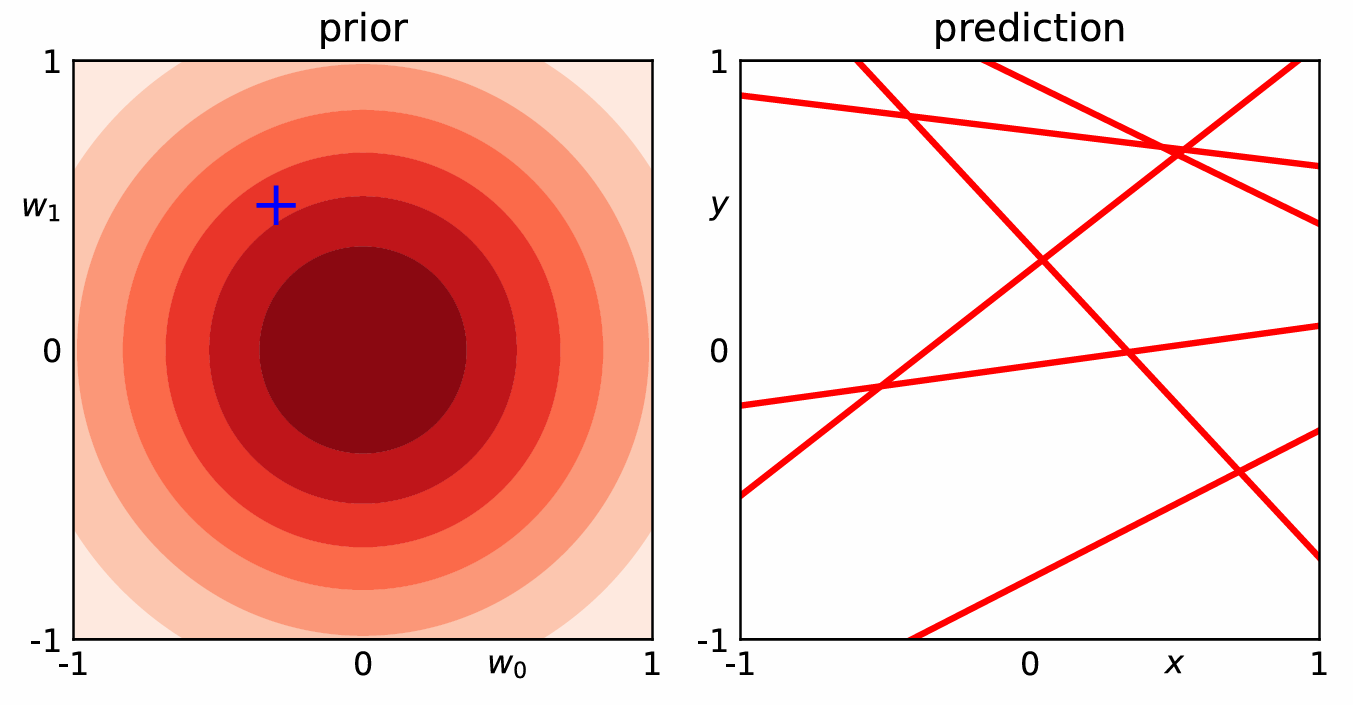
1. 先验阶段：无数据时，参数分布（prior）集中在初始猜测附近，预测（prediction）是分散的直线
2. 少量数据：后验分布（posterior）向数据方向偏移，预测直线开始集中
3. 更多数据：后验分布更集中，预测直线收敛到拟合数据的趋势
4. 强正则化 / 弱正则化 ：
   • ln ⁡ λ \ln \lambda lnλ 越小（正则化越弱），后验分布越分散、预测波动越大
   • ln ⁡ λ \ln \lambda lnλ 越大（正则化越强），后验越集中、预测越稳定

3.数据量对模型参数和预测结果的影响

颜色越深代表 "这个参数组合出现的概率越高"

还没看数据时，参数的 "先验分布" 是一堆同心圆:

(预测线是乱的, 因为参数不确定)

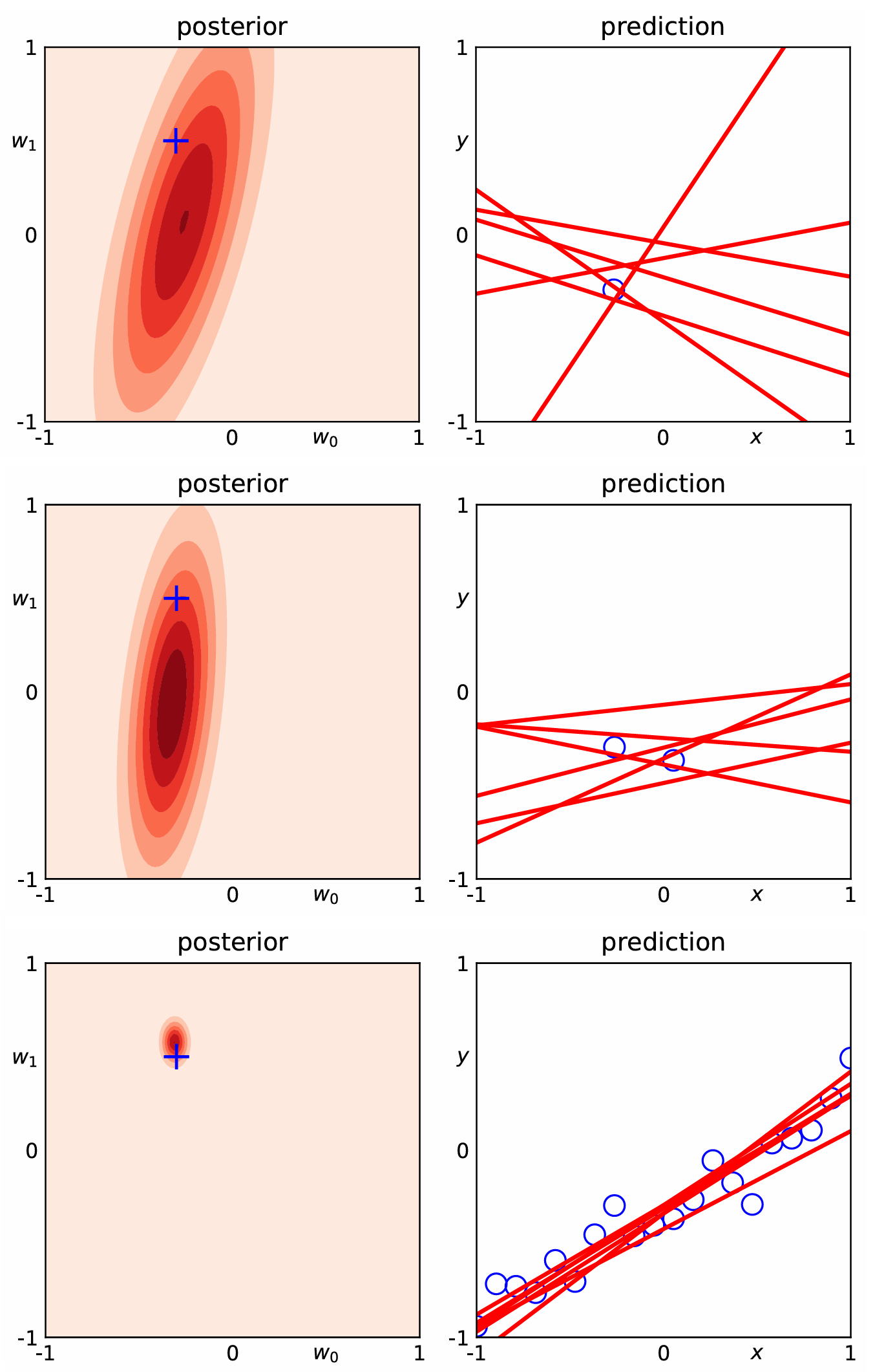
随着数据变多，参数的 "后验分布" 从 "扁椭圆" 变成 "小圆圈":

-> 说明数据让我们对参数的猜测越来越精准（分布越来越集中）

(随着数据变多，红色直线越来越 "挤在一起"，最后几乎重合)

例题

在机器学习模型中引入 L 2 L_2 L2正则化项的目的是什么? 其工作原理是什么?

答:

防止模型过拟合（即模型在训练数据上表现好，但泛化能力差）

在损失函数中加入模型参数的L2范数，迫使参数取值更小，降低模型复杂度，避免对训练数据的 "过度拟合", 学习到噪声