Abs Function - Derivatives and Gradients (导数和梯度)

Yongqiang Cheng2026-01-06 15:22

Abs Function - Derivatives and Gradients {导数和梯度}

  • [1. Abs (Absolute Value) Function](#1. Abs (Absolute Value) Function)
    • [1.1. Parameters](#1.1. Parameters)
    • [1.2. Keyword Arguments](#1.2. Keyword Arguments)
  • [2. Abs Function - Derivatives and Gradients (导数和梯度)](#2. Abs Function - Derivatives and Gradients (导数和梯度))
    • [2.1. PyTorch `torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor`](#2.1. PyTorch torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor)
    • [2.2. PyTorch `torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor`](#2.2. PyTorch torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor)
    • [2.3. Python Abs Function](#2.3. Python Abs Function)
    • [2.4. Python Abs Function](#2.4. Python Abs Function)
  • References

1. Abs (Absolute Value) Function

torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor
https://docs.pytorch.org/docs/stable/generated/torch.abs.html

torch.absolute(input: Tensor, *, out: Optional[Tensor]) -> Tensor
https://docs.pytorch.org/docs/stable/generated/torch.absolute.html

Alias for torch.abs().

Computes the absolute value of each element in input.

The absolute value of a number is the number without a sign.

复制代码 
sign [saɪn]
v. 签名；签署；叹息；预示
n. 符号；信号；表示；招牌

The definition of the Abs function:

out i = ∣ input i ∣ \text{out}{i} = |\text{input}{i}| outi=∣inputi∣

In mathematics, the absolute value or modulus of a real number x x x, denoted ∣ x ∣ |x| ∣x∣, is the non-negative value of x x x without regard to its sign. Namely, ∣ x ∣ = x {\displaystyle |x|=x} ∣x∣=x if x {\displaystyle x} x is a positive number, and ∣ x ∣ = − x {\displaystyle |x|=-x} ∣x∣=−x if x {\displaystyle x} x is negative (in which case negating x {\displaystyle x} x makes − x {\displaystyle -x} −x positive), and ∣ 0 ∣ = 0 {\displaystyle |0|=0} ∣0∣=0.

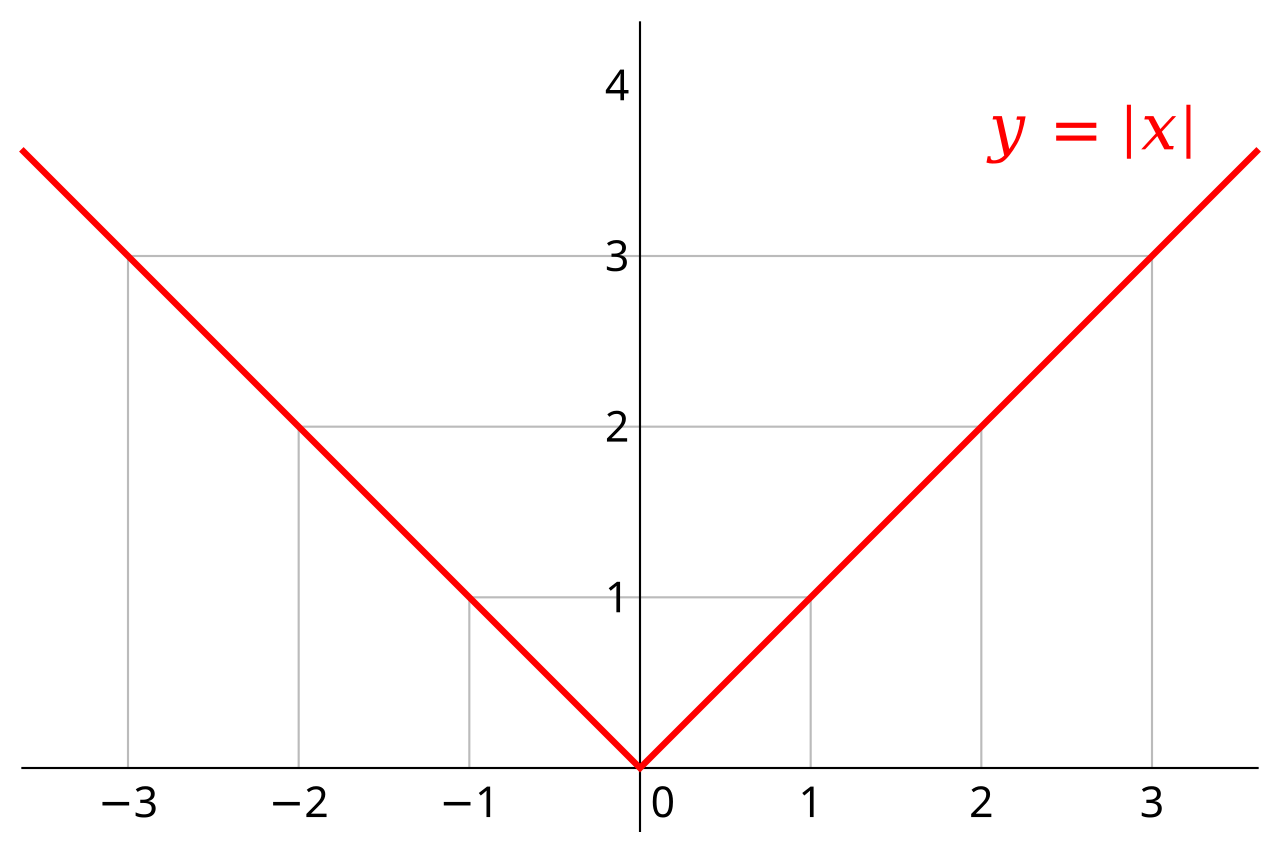
Abs ( x ) = ∣ x ∣ = { x , x ≥ 0 − x , x < 0 \begin{aligned} \text{Abs}(x) &= |x| \\ &= \begin{cases} x, & x \geq 0\\ -x, & x < 0\\ \end{cases} \\ \end{aligned} Abs(x)=∣x∣={x,−x,x≥0x<0

The absolute value of x {\displaystyle x} x is thus always either a positive number or zero, but never negative. When x {\displaystyle x} x itself is negative ( x < 0 {\displaystyle x<0} x<0), then its absolute value is necessarily positive ( ∣ x ∣ = − x > 0 {\displaystyle |x|=-x>0} ∣x∣=−x>0).

The absolute value function of a real number returns its value irrespective of its sign, whereas the sign (or signum) function returns a number's sign irrespective of its value.

实数的绝对值函数返回该数的数值，而不考虑其正负号；而符号函数或正负号函数返回该数的正负号，而不考虑其数值大小。

The following equations show the relationship between these two functions:
∣ x ∣ = x sgn ⁡ ( x ) , {\displaystyle |x|=x\operatorname {sgn} (x),} ∣x∣=xsgn(x),

or
∣ x ∣ sgn ⁡ ( x ) = x , {\displaystyle |x|\operatorname {sgn} (x)=x,} ∣x∣sgn(x)=x,

and for x ≠ 0 x \neq 0 x=0,
sgn ⁡ ( x ) = ∣ x ∣ x = x ∣ x ∣ . {\displaystyle \operatorname {sgn} (x)={\frac {|x|}{x}}={\frac {x}{|x|}}.} sgn(x)=x∣x∣=∣x∣x.

The derivative of the Abs function:

d y d x = f ′ ( x ) = d ( { x , x ≥ 0 − x , x < 0 ) d x = { 1 , x > 0 0 ( common convention ) , x = 0 − 1 , x < 0 \begin{aligned} \frac{dy}{dx} &= f'(x) \\ &= \frac{d \left( \begin{cases} x, & x \geq 0\\ -x, & x < 0\\ \end{cases} \right) }{dx} \\ &= \begin{cases} 1, & x > 0\\ 0 \ (\text{common convention}), & x = 0\\ -1, & x < 0\\ \end{cases} \\ \end{aligned} dxdy=f′(x)=dxd({x,−x,x≥0x<0)=⎩ ⎨ ⎧1,0 (common convention),−1,x>0x=0x<0

The derivative is undefined at x = 0 x=0 x=0. In practice, deep learning frameworks like PyTorch or TensorFlow return 0 0 0 at this point.

The derivative is the sign function. At x = 0 x=0 x=0, the derivative is technically undefined, but frameworks typically default to 0 0 0.

1.1. Parameters

  • input (Tensor) - the input tensor.

1.2. Keyword Arguments

  • out (Tensor, optional) - the output tensor.

    !/usr/bin/env python

    coding=utf-8

    import torch
    from matplotlib import pyplot as plt

    def plot(X, Y=None, xlabel=None, ylabel=None, legend=[], xlim=None, ylim=None, xscale='linear', yscale='linear',
    fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """
    https://github.com/d2l-ai/d2l-en/blob/master/d2l/torch.py
    """

    复制代码 
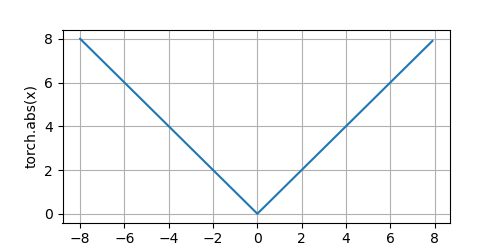
      def has_one_axis(X):  # True if X (tensor or list) has 1 axis
      return ((hasattr(X, "ndim") and (X.ndim == 1)) or (isinstance(X, list) and (not hasattr(X[0], "__len__"))))

  if has_one_axis(X): X = [X]

  if Y is None:
      X, Y = [[]] * len(X), X
  elif has_one_axis(Y):
      Y = [Y]

  if len(X) != len(Y):
      X = X * len(Y)

  # Set the default width and height of figures globally, in inches.
  plt.rcParams['figure.figsize'] = figsize

  if axes is None:
      axes = plt.gca()  # Get the current Axes

  # Clear the Axes
  axes.cla()

  for x, y, fmt in zip(X, Y, fmts):
      axes.plot(x, y, fmt) if len(x) else axes.plot(y, fmt)

  axes.set_xlabel(xlabel), axes.set_ylabel(ylabel)  # Set the label for the x/y-axis
  axes.set_xscale(xscale), axes.set_yscale(yscale)  # Set the x/y-axis scale
  axes.set_xlim(xlim), axes.set_ylim(ylim)  # Set the x/y-axis view limits

  if legend:
      axes.legend(legend)  # Place a legend on the Axes

  # Configure the grid lines
  axes.grid()

  plt.show()
  plt.savefig("yongqiang.png", transparent=True)  # Save the current figure

    x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
    y = torch.abs(x)
    plot(x.detach(), y.detach(), 'x', 'torch.abs(x)', figsize=(5, 2.5))

    Clear out previous gradients

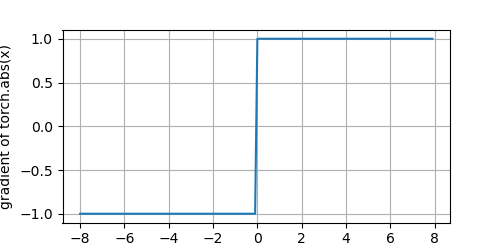
    x.grad.data.zero_()

    y.backward(torch.ones_like(x), retain_graph=True)
    plot(x.detach(), x.grad, 'x', 'gradient of torch.abs(x)', figsize=(5, 2.5))

The Abs function:

The derivative of the Abs function:

2. Abs Function - Derivatives and Gradients (导数和梯度)

Notes

  • Element-wise Multiplication (Hadamard Product) (* operator or numpy.multiply()): Multiplies corresponding elements of two arrays that must have the same shape (or be broadcastable to a common shape).
  • Matrix Multiplication (Dot Product) (@ operator or numpy.matmul() or numpy.dot()): Performs the standard linear algebra operation that requires specific dimension compatibility rules. (e.g., the number of columns in the first array must match the number of rows in the second).

2.1. PyTorch torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor

复制代码 
# !/usr/bin/env python
# coding=utf-8

import torch
import torch.nn as nn

torch.set_printoptions(precision=6)

input = torch.tensor([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=torch.float, requires_grad=True)

print(f"input.requires_grad: {input.requires_grad}, input.shape: {input.shape}")

forward_output = torch.abs(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

forward_output.backward(torch.ones_like(input), retain_graph=True)

print(f"\nbackward_output.shape: {input.grad.shape}")
print(f"Backward Pass Output:\n{input.grad}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/abs.py 
input.requires_grad: True, input.shape: torch.Size([2, 3])

forward_output.shape: torch.Size([2, 3])
Forward Pass Output:
tensor([[1.500000, 0.000000, 1.500000],
        [0.500000, 2.000000, 3.000000]], grad_fn=<AbsBackward0>)

backward_output.shape: torch.Size([2, 3])
Backward Pass Output:
tensor([[-1.,  0.,  1.],
        [ 1., -1.,  1.]])

Process finished with exit code 0

2.2. PyTorch torch.abs(input: Tensor, *, out: Optional[Tensor]) -> Tensor

复制代码 
# !/usr/bin/env python
# coding=utf-8

import torch
import torch.nn as nn

torch.set_printoptions(precision=6)

input = torch.tensor([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=torch.float, requires_grad=True)

print(f"input.requires_grad: {input.requires_grad}, input.shape: {input.shape}")

forward_output = torch.abs(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

forward_output.backward(torch.ones_like(input), retain_graph=True)

print(f"\nbackward_output.shape: {input.grad.shape}")
print(f"Backward Pass Output:\n{input.grad}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/abs.py 
input.requires_grad: True, input.shape: torch.Size([6])

forward_output.shape: torch.Size([6])
Forward Pass Output:
tensor([1.500000, 0.000000, 1.500000, 0.500000, 2.000000, 3.000000],
       grad_fn=<AbsBackward0>)

backward_output.shape: torch.Size([6])
Backward Pass Output:
tensor([-1.,  0.,  1.,  1., -1.,  1.])

Process finished with exit code 0

2.3. Python Abs Function

复制代码 
# !/usr/bin/env python
# coding=utf-8

import numpy as np


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class AbsLayer:
    """
    A class to represent the Abs layer for a neural network.
    """

    def __init__(self):
        # Cache the input for the backward pass
        self.input = None

    def forward(self, input):
        """
        Forward Pass: f(x) = abs(x)
        Computes the element-wise absolute value
        """

        self.input = input
        output = np.abs(input)
        return output

    def backward(self, upstream_gradient):
        """
        Backward Pass (Backpropagation): f'(x) = -1 if x < 0, 0 if x == 0, 1 if x > 0
        The derivative of |x| is the sign function, np.sign(0) returns 0 by default in NumPy
        The total gradient is the element-wise product of the upstream
        gradient and the derivative of the Log.
        """

        abs_derivative = np.sign(self.input)
        print(f"abs_derivative.shape: {abs_derivative.shape}")
        print(f"Abs Derivative:\n{abs_derivative}")

        # upstream_gradient: the gradient of the loss with respect to the output
        # Computes the gradient of the loss with respect to the input (dL/dx)
        # Apply the chain rule: multiply the derivative by the upstream gradient
        # dL/dx = dL/dy * dy/dx = upstream_gradient * f'(x)
        downstream_gradient = upstream_gradient * abs_derivative
        return downstream_gradient


layer = AbsLayer()

input = np.array([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=np.float32)

# Forward pass
forward_output = layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/abs.py 

forward_output.shape: (2, 3)
Forward Pass Output:
[[1.5 0.  1.5]
 [0.5 2.  3. ]]
abs_derivative.shape: (2, 3)
Abs Derivative:
[[-1.  0.  1.]
 [ 1. -1.  1.]]

backward_output.shape: (2, 3)
Backward Pass Output:
[[-0.1  0.   0.1]
 [ 0.1 -0.1  0.1]]

Process finished with exit code 0

2.4. Python Abs Function

复制代码 
# !/usr/bin/env python
# coding=utf-8

import numpy as np


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class AbsLayer:
    """
    A class to represent the Abs layer for a neural network.
    """

    def __init__(self):
        # Cache the input for the backward pass
        self.input = None

    def forward(self, input):
        """
        Forward Pass: f(x) = abs(x)
        Computes the element-wise absolute value
        """

        self.input = input
        output = np.abs(input)
        return output

    def backward(self, upstream_gradient):
        """
        Backward Pass (Backpropagation): f'(x) = -1 if x < 0, 0 if x == 0, 1 if x > 0
        The derivative of |x| is the sign function, np.sign(0) returns 0 by default in NumPy
        The total gradient is the element-wise product of the upstream
        gradient and the derivative of the Log.
        """

        abs_derivative = np.sign(self.input)
        print(f"abs_derivative.shape: {abs_derivative.shape}")
        print(f"Abs Derivative:\n{abs_derivative}")

        # upstream_gradient: the gradient of the loss with respect to the output
        # Computes the gradient of the loss with respect to the input (dL/dx)
        # Apply the chain rule: multiply the derivative by the upstream gradient
        # dL/dx = dL/dy * dy/dx = upstream_gradient * f'(x)
        downstream_gradient = upstream_gradient * abs_derivative
        return downstream_gradient


layer = AbsLayer()

input = np.array([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=np.float32)

# Forward pass
forward_output = layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/abs.py 

forward_output.shape: (6,)
Forward Pass Output:
[1.5 0.  1.5 0.5 2.  3. ]
abs_derivative.shape: (6,)
Abs Derivative:
[-1.  0.  1.  1. -1.  1.]

backward_output.shape: (6,)
Backward Pass Output:
[-0.1  0.   0.1  0.1 -0.1  0.1]

Process finished with exit code 0

References

1\] Yongqiang Cheng (程永强), \[2\] 动手学深度学习, \[3\] Deep Learning Tutorials, \[4\] Gradient boosting performs gradient descent, \[5\] Matrix calculus, \[6\] Artificial Inteligence,

相关推荐
Yongqiang Cheng4 天前
Softplus Function - Derivatives and Gradients (导数和梯度)
梯度·导数·gradients·derivatives·softplus
課代表6 天前
从初等数学到高等数学
算法·微积分·函数·极限·导数·积分·方程
点云SLAM6 天前
Derivative 英文单词学习
导数·英文单词学习·雅思备考·derivative·派生物 / 衍生量·非原创的 / 模仿性的
Yongqiang Cheng10 天前
SELU Function - Derivatives and Gradients (导数和梯度)
梯度·导数·gradients·derivatives·selu
Yongqiang Cheng16 天前
ELU Function - Derivatives and Gradients (导数和梯度)
梯度·导数·gradients·derivatives·elu
Yongqiang Cheng17 天前
Tanh Function - Derivatives and Gradients (导数和梯度)
梯度·导数·tanh·gradients·derivatives
Yongqiang Cheng18 天前
ReLU Function and Leaky ReLU Function - Derivatives and Gradients (导数和梯度)
梯度·导数·relu·gradients·derivatives·leaky relu
小毅&Nora18 天前
【数学】【微积分】 ③ 导数的核心应用：从变化率到现实世界优化
微积分·导数
Yongqiang Cheng1 个月前
Mean Absolute Error (MAE) Loss Function - Derivatives and Gradients (导数和梯度)
梯度·导数·mae·gradients·loss function·derivatives
热门推荐
01GitHub 镜像站点02安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）03Labelme从安装到标注：零基础完整指南04Linux下V2Ray安装配置指南05【踩坑笔记】50系显卡适配的 PyTorch 安装06手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！07GitLab 零基础入门指南：从安装到项目管理全流程08jdk21下载、安装（Windows、Linux、macOS）09UV安装并设置国内源102025-04-03 Latex学习1——本地配置Latex + VScode环境