代码随想录刷题——二叉树篇（九）

cpp 复制代码

class Solution{
public:
	void traversal(TreeNode* node,vector<int>& path,vector<string>& ans){
		path.push_back(node->val);
		if(!node->left&&!node->right){
			string sPath;
			for(int i=0;i<path.size()-1;i++){
				sPath += to_string(path[i]);
				sPath += "->";
			}
			sPath += to_string(path[path.size()-1]);
			ans.push_back(sPath);
		}
		if(node->left){
			traversal(node->left,path,ans);
			path.pop_back();
		}
		if(node->right){
			traversal(node->right,path,ans);
			path.pop_back();
		}
		return ;
	} 
	vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> ans;
        vector<int> path;
		if(!root) return ans;
		traversal(root,path,ans);
		return ans;
    }
};

迭代+回溯：

cpp 复制代码

class Solution{
public:
	vector<string> binaryTreePaths(TreeNode* root){
		vector<string> ans;
		if(!root) return ans;
		queue<TreeNode*> qu;
		queue<string> qs;
		qu.push(root);
		qs.push(to_string(root->val));
		while(!qu.empty()){
			TreeNode* node=qu.front();
			qu.pop();
			string path=qs.front();
			qs.pop();
			if(!node->left&&!node->right){
				ans.push_back(path);
			} 
			if(node->right){
				qu.push(node->right);
				qs.push(path+"->"+to_string(node->right->val));
			}
			if(node->left){
				qu.push(node->left);
				qs.push(path+"->"+to_string(node->left->val));
			}
		}
		return ans;
	}
};

其他：

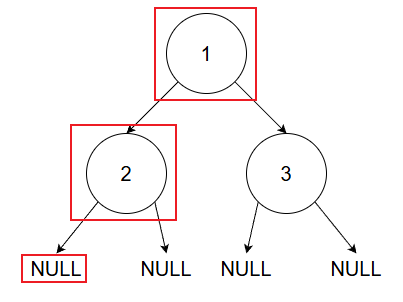
（1）递归新理解：想象一棵如下图所示的树，从NULL开始，分三种情况 向上分别思考。考虑终止处理逻辑出现在哪一层，以及需要的处理逻辑是什么样的。因为红框框起来的三个节点代表了递归中的三种情况：一是空节点，二是叶子节点，三是连接叶子节点的节点

这样的好处在于，三种节点的情况由简单到复杂，同时也是递归本身的总体顺序（从下往上），便于理清递归的整体逻辑。

（3）递归和回溯：

a.递归和回溯要在一起

b.递归和回溯时，共享变量 就像是记录情况的进度条，有增有减

（4）迭代和回溯：

a.只要是回溯，就应该有记录情况的进度条

b.迭代时的回溯更像是复制了多次备份

迭代法这里用于遍历的容器适配器 必须和用于存储string的容器适配器一致，如果一个是queue、另一个是stack，顺序就不对了

（5）to_string()的使用