1 今日打卡
组合总和Ⅲ 216. 组合总和 III - 力扣(LeetCode)
电话号码的字母总和 17. 电话号码的字母组合 - 力扣(LeetCode)
2 组合
2.1 思路
动作 1:终止条件(停止递归的依据)
逻辑:path.size() == k
目的:当前选好的数字个数等于 k 时,说明这是一个合法组合,必须保存下来;
细节:res.add(new ArrayList<>(path)) 而不是 res.add(path):因为 path 是全局的,后续会被修改(比如移除元素),如果直接加引用,res 里的内容会跟着变,最终全是空列表。
动作 2:遍历选择列表(控制可选范围)
逻辑:for(int i = startIndex; i <= n; i++)
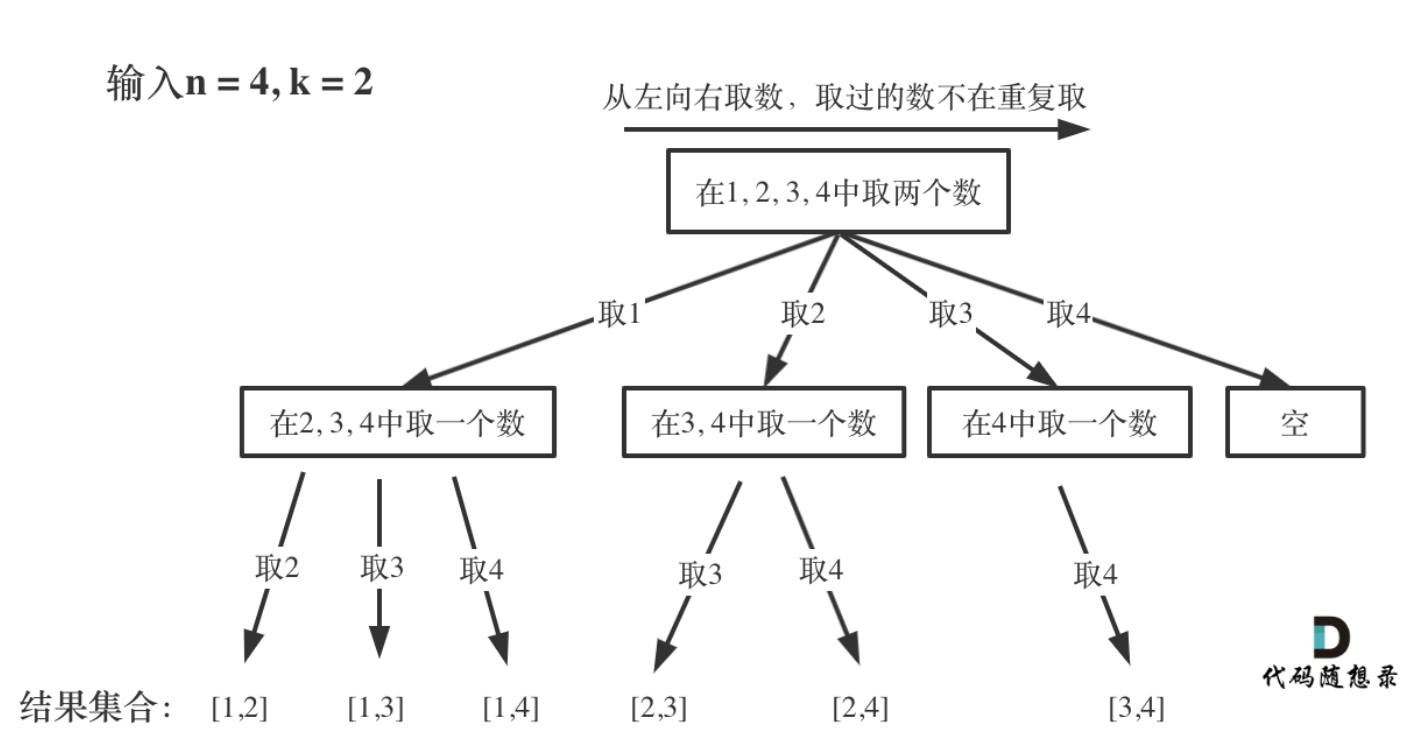
核心目的:避免重复组合(组合不考虑顺序);
比如第一轮选了 1,下一轮只能从 2 开始选(startIndex=2),不会再选 1,因此不会出现 [1,2] 和 [2,1] 这种重复;
如果去掉 startIndex,直接从 1 开始遍历,会生成大量重复组合(比如 [1,2]、[2,1]、[1,1] 等),不符合要求。
动作 3:做选择(构建路径)
逻辑:path.add(i)
目的:把当前选中的数字加入路径,扩展当前组合的长度(比如 path=[1] 加入 2 后变成 [1,2])。
动作 4:递归(深入穷举)
逻辑:backtracking(n, k, i + 1)
目的:基于当前选择(选了 i),继续从 i+1 开始选下一个数字,直到路径长度达标(触发终止条件)。
动作 5:撤销选择(回溯的核心)
逻辑:path.remove(path.size() - 1)
目的:回到选当前数字之前的状态,尝试选择列表中的下一个数字;
比如选了 1→2 后,触发终止条件保存 [1,2],然后撤销 2(path 回到 [1]),再选 3,生成 [1,3],以此类推;
如果不撤销,path 会一直累加(比如变成 [1,2,3]),无法构建新的组合。
2.2 实现代码
java
class Solution {
// 1. 全局变量:path记录当前组合,res记录所有符合条件的组合
List<Integer> path = new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
// 主方法:对外暴露的接口,调用回溯函数后返回结果
public List<List<Integer>> combine(int n, int k) {
backtracking(n, k, 1); // 回溯入口:从数字1开始选
return res;
}
// 核心回溯函数:参数说明
// n:可选数字的最大值(1~n)
// k:需要选的数字个数
// startIndex:本轮选数的起始位置(避免重复组合)
public void backtracking(int n, int k, int startIndex) {
// 2. 递归终止条件:当前组合的长度等于k,说明选够了
if(path.size() == k) {
// 把当前组合的副本加入结果集(必须new ArrayList,否则res会引用同一个path)
res.add(new ArrayList<>(path));
return; // 终止当前递归,回到上一层
}
// 3. 遍历:从startIndex开始,逐个选择数字
for(int i = startIndex; i <= n; i++) {
// 3.1 选择:把当前数字i加入当前组合path
path.add(i);
// 3.2 递归:选完i后,下一轮从i+1开始选(避免重复)
backtracking(n, k, i + 1);
// 3.3 回溯:撤销选择的i,回到选i之前的状态,尝试选下一个数字
path.remove(path.size() - 1);
}
}
}2.3 剪枝优化
java
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backtracking(n, k, 1);
return res;
}
public void backtracking(int n, int k, int startIndex) {
if(path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
for(int i = startIndex; i <= n - (k - path.size()) + 1; i++) {
path.add(i);
backtracking(n, k, i + 1);
path.remove(path.size() - 1);
}
}
}已经选择的元素个数:path.size();
所需需要的元素个数为: k - path.size();
列表中剩余元素(n-i) >= 所需需要的元素个数(k - path.size())
在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1,开始遍历
3 组合总和Ⅲ
3.1 思路
两个关键剪枝(效率核心)
剪枝的目的是提前终止无效分支,减少递归次数,这段代码有两个核心剪枝:
剪枝 1(sum 超界):if (sum > n) return;
比如 k=3、n=7,path=[4,5](sum=9>7),后续加任何数字 sum 都会更大,直接返回,不做无用功。
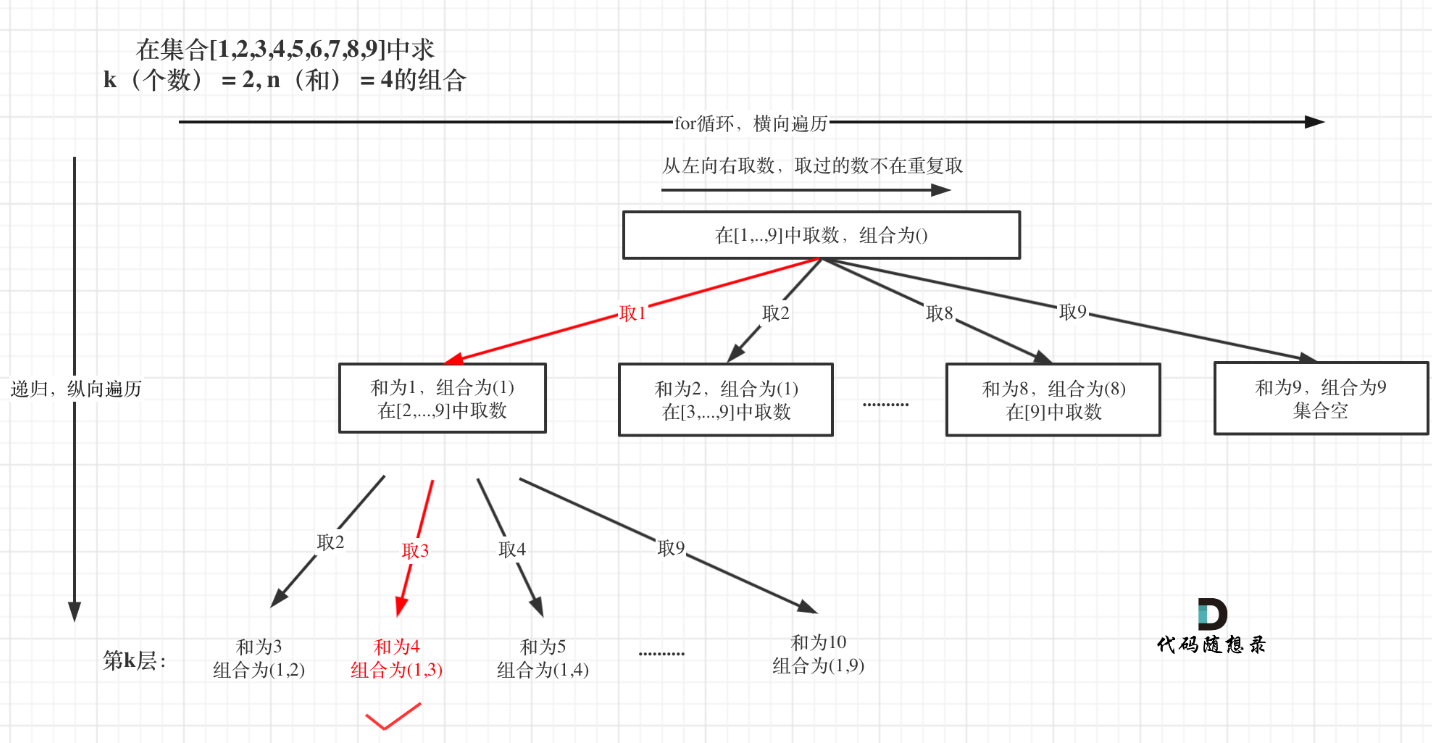
剪枝 2(数字范围 + 数量足够):i <= 9 - (k - path.size()) + 1
既限制了数字只能到 9(组合总和 Ⅲ 的规则),又保证从 i 开始有足够数字选够 k 个(比如 k=3、path.size ()=1,i 最大到 8,因为 8、9 刚好 2 个数字)。
在收集结果的时候,不能用path.size() == k && sum == n作为判断条件,因为选够了k个数字,但是和不是n的话,代码没有触发 return,会继续执行后面的 for 循环,而循环会不断递归调用自身,最终超出栈的容量。
3.2 代码实现
java
class Solution {
// 全局变量1:记录当前正在构建的组合(路径),比如选了1、2,path=[1,2]
List<Integer> path = new ArrayList<>();
// 全局变量2:收集所有符合条件的组合(最终结果集)
List<List<Integer>> res = new ArrayList<>();
// 全局变量3:记录当前path中所有数字的和,避免每次遍历path计算和(提升效率)
int sum = 0;
// 主方法:对外暴露的接口,返回所有符合条件的组合
// k:要求选的数字个数;n:要求数字的和
public List<List<Integer>> combinationSum3(int k, int n) {
// 调用回溯函数,从数字1开始选(startIndex=1,避免重复组合)
backtracking(k, n, 1);
return res;
}
// 核心回溯函数
// k:需要选的数字总数;n:目标和;startIndex:本轮选数的起始位置(去重关键)
public void backtracking(int k, int n, int startIndex) {
// 剪枝1:提前终止无效分支
// 如果当前sum已经超过n,后续加数字只会更大,不可能等于n,直接返回
if (sum > n) {
return;
}
// 递归终止条件1:已经选够k个数字
if (path.size() == k) {
// 只有当前sum等于目标n时,才是符合条件的组合,加入结果集
if (sum == n) {
// 必须new ArrayList<>(path):保存path的副本,避免后续回溯修改res中的内容
res.add(new ArrayList<>(path));
}
// 无论sum是否等于n,选够k个数字都要返回(不够的话也凑不齐了)
return;
}
// 遍历选择列表:从startIndex开始选,避免重复组合
// 剪枝2:i <= 9 - (k - path.size()) + 1
// 解释:
// 1. 9:组合总和Ⅲ的数字范围固定是1~9,i不能超过9;
// 2. 9 - (k - path.size()) + 1:保证从i开始还有足够的数字选够k个(比如k=3,path.size()=1,还需选2个,i最大只能是8,因为8、9刚好2个)
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
// 1. 做选择:把当前数字i加入路径
path.add(i);
// 2. 累加和:更新当前组合的和
sum += i;
// 3. 递归:基于当前选择,继续选下一个数字(startIndex=i+1,避免重复选同一个数字)
backtracking(k, n, i + 1);
// 4. 回溯(撤销选择):先减和,再移除数字,回到选i之前的状态
sum -= i;
path.remove(path.size() - 1);
}
}
}4 电话号码的字母组合
4.1 思路
用str数组来存储字符串,加两个空串更方便一点。
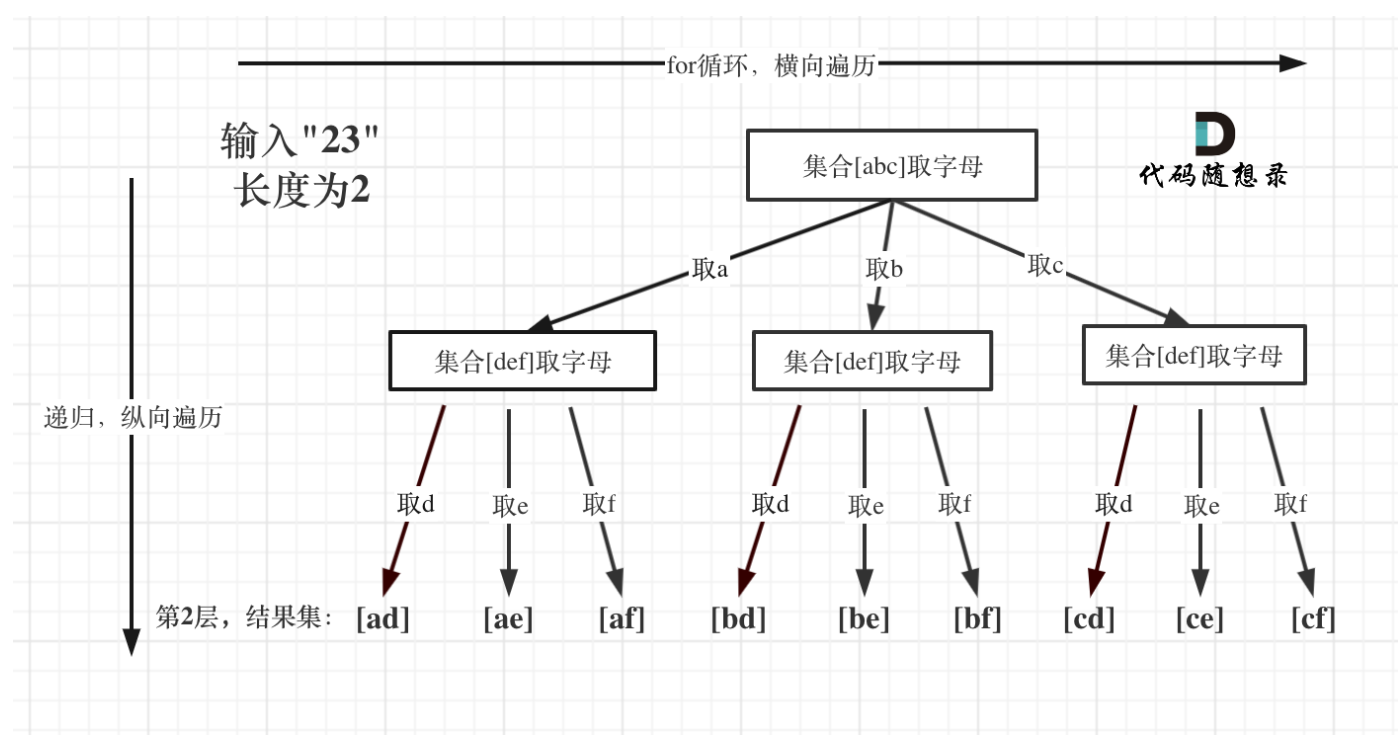
回溯函数参数:传入digits、index,index表示 "当前处理到数字字符串的第几个数字",而非普通组合的startIndex;普通组合的startIndex是为了 "去重 / 避免回头选",而这里的index是为了 "按顺序处理每个数字"(比如先处理第 0 位的 2,再处理第 1 位的 3),每一层递归对应一个数字的处理。
终止条件:sb的长度等于index时,表示所有输入字符都处理完了。
单层处理:用for循环遍历当前层的字符串cur。每加入一个就递归调用函数,index深度+1。等回溯回来的时候,再继续本层的for循环,直到遍历完所有元素。
4.2 实现代码
java
class Solution {
// 最终结果集:存储所有符合条件的字母组合
List<String> res = new ArrayList<>();
// 路径:记录当前正在构建的字母组合(StringBuilder比String高效,适合频繁增删)
StringBuilder sb = new StringBuilder();
// 数字到字母的映射表:索引对应数字(0/1无对应字母,2对应abc,以此类推)
String[] str = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
// 主方法:输入数字字符串,返回所有字母组合
public List<String> letterCombinations(String digits) {
// 边界条件:如果输入为空字符串,直接返回空结果(避免空递归)
if (digits == null || digits.length() == 0) {
return res;
}
// 回溯入口:从第0个数字开始处理
backtracking(digits, 0);
return res;
}
// 核心回溯函数
// digits:输入的数字字符串
// index:当前处理到digits的第几个数字(递归层级标识)
public void backtracking(String digits, int index) {
// 递归终止条件:处理完所有数字(index等于数字字符串长度)
if (index == digits.length()) {
// 将当前构建好的字母组合加入结果集
res.add(sb.toString());
return; // 终止当前递归分支,回溯到上一层
}
// 1. 获取当前处理的数字(字符转数字:'2'-'0'=2)
int number = digits.charAt(index) - '0';
// 2. 获取当前数字对应的字母串(比如数字2对应"abc")
String cur = str[number];
// 3. 遍历当前数字对应的所有字母(选择列表)
for (int i = 0; i < cur.length(); i++) {
// 做选择:将当前字母加入路径
sb.append(cur.charAt(i));
// 递归:处理下一个数字(index+1,进入下一层递归)
backtracking(digits, index + 1);
// 回溯:撤销选择,删除最后一个字母(回到选当前字母前的状态)
sb.deleteCharAt(sb.length() - 1);
}
}
}