二元分类，机器学习为什么可行？

背景

为什么我们说机器学习一定能从我们数据集中学到东西，有无理论证明？

霍夫丁不等式

为了证明这个问题，于是有了霍夫丁不等式。

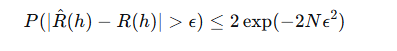
对于一个固定的假设 h，只要训练数据足够多（N 大），训练误差大概率接近真实误差。

问题

但这只能保证单个固定假设，而我们训练时会从假设集中选择表现最好的那个！

但是当前表现最好的就一定是最接近f(x)的吗？

好的h 总是相似的，不好的h各有各的不好

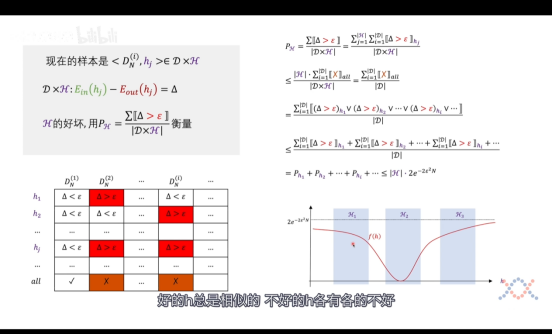
对于单个的h，我们无法确定其距离真实的f(x)相差多少，无法评判h的好坏。但是如果对于一群h（后续写作H），我们就能评判其好坏，因为好的h总是相似的，不好的h各有各的不好。

以一个笛卡尔乘积的形式列下来，只要有一个h在Di中犯了错，那么就认为最终的h all是坏的情况。所以我们可以得到：Ph_i <= Ph_all <= |H| * 2e^(-2N(期望^2))。

其中：|H|所表达的意义就是所有可能的h的个数

不过：H****不是训练过程中选出来的，而是在训练之前就由模型架构确定的。

模型设计 = 设计****H ，模型训练 = 从H中选****h。VC维理论告诉我们如何根据数据量来设计合适的H，从而保证学习可行。

H****分类无限转有限

进一步推导，以线性分类器为例。

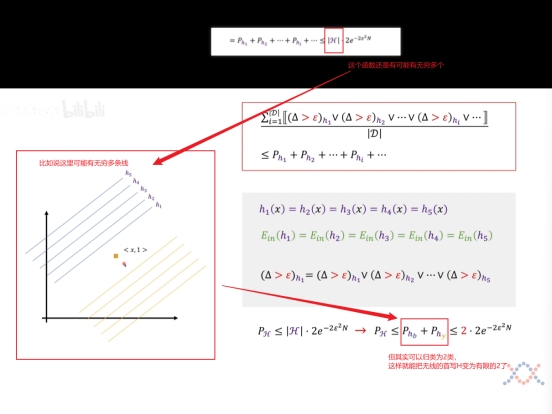
增加一个数据点则可以拿到四类曲线，我们可以归类出来了2^N这个指数级别函数了。分母指数级别递增增长，因此无上界限，所以我们无法确定这个坏事情发生的概率是否会随着N的增加而变小，所以我们要继续推导，能否把2^N****降级！

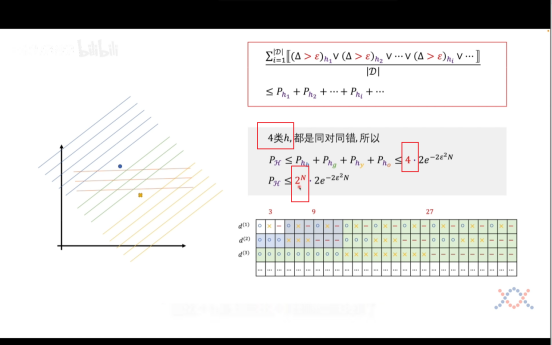
不等式右界降级

但其实我们继续往后推理，会发现其实并不会永远遵循2^N的规律，

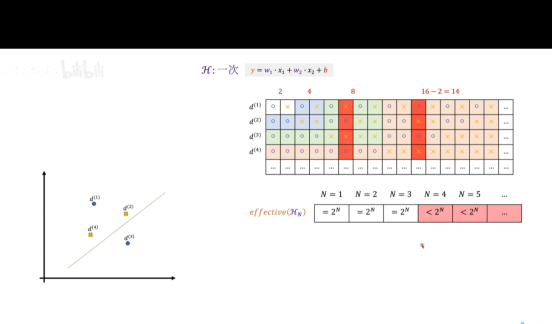
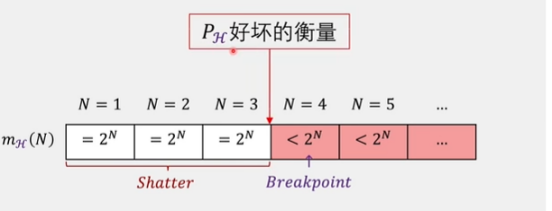
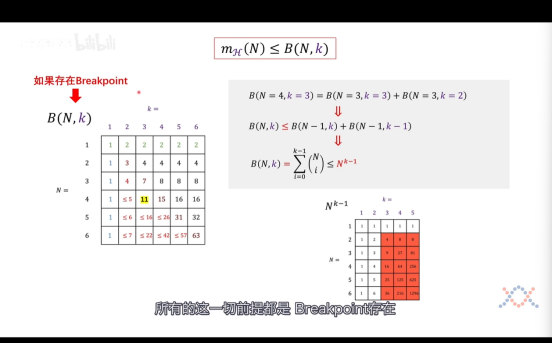
往后继续推论我们可以知道这样的h个数是**不会超过N^(k-1)的，至此，我们已经证明了 霍夫丁不等式**式子是可行的了，**随着N****数据集的增多，我们训练出来的模型表现坏的概率就越小**

最后得到式子如下，记住结论即可。

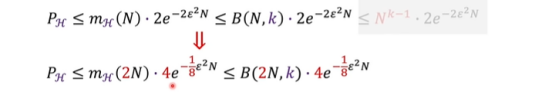
**VC **维

对于线性分类器（d维）：dVC=d+1

VC维的深刻意义

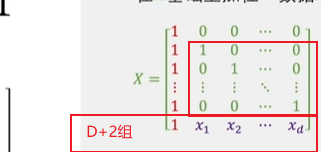
d是空间维度

上图中，在d+2组之前，存在某种情况可以使得所有的向量都是线性无关的（数学意义就是在整个空间中所有的点都能被d+2组之前的向量所表示），所以加入的d+2组数据，一定是能被目前空间中的数据所表示的，那么就表示这不是新的一类数据（也就无法被h函数所分割，无法产生新的h函数）。

d+1分别代表的含义如下

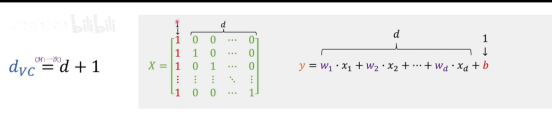
总结

因此，机器学习可行的充要条件是：

Appendix

哔哩哔哩王木头