TL;DR
- 场景：从机器学习视角系统理解线性回归（表示形式、目标函数、参数求解）
- 结论：线性回归=线性预测函数+SSE损失最小化；最小二乘可导出正规方程解
- 产出：得到从标量到矩阵的统一表达、SSE定义、最小二乘/多元求解推导路径
概述
在正式进入到回归分析的相关算法讨论之前，我们需要对监督学习算法中的回归问题进一步进行分析和理解。虽然回归问题同属于有监督的学习范畴，但实际上，回归问题要远比分类问题更加复杂。 首先关于输出结果的对比，分类模型最终输出结果为离散变量，而离散变量本身包含信息量较少，其本身并不具备代数运算性质，因此其评价指标体系也较为简单，最常用的就是混淆矩阵以及ROC 曲线。 而回归问题最终输出的是连续变量，其本身不仅能够代表运算，且还具有更精致的方法，希望对事物运行的更底层原理进行挖掘。即回归问题的模型更加全面、完善的描绘了事物客观规律，从而能够得到更加细粒度的结论。因此，回归问题的模型往往更加复杂，建模所需要数据所提供的信息量也越多，进而在建模过程中可能遇到的问题也越多。
线性回归与机器学习
线性回归问题是解决回归类问题最常用使用的算法模型，其算法思想和基本原理都是由多元统计分析发展而来，但在数据挖掘和机器学习领域中，也是不可多得的行之有效的算法模型。一方面，线性回归蕴藏的机器学习思想非常值得借鉴和学习，并且随着时间发展，在线性回归的基础上还诞生了许多强大的非线性模型。 因此，我们在进行机器学习算法学习过程中，仍然需要对线性回归这个统计分析算法进行系统深入的学习。但这需要说明的是，线性回归的建模思想有很多理解的角度，此处我们并不需要从统计学的角度上理解、掌握和应用线性回归算法，很多时候，利用机器学习的思维来理解线性回归，会是一种更好的理解方法，这也将是我们这部分内容讲解线性回归的切入角度。
线性回归的机器学习表示方法
核心逻辑
任何机器学习算法首先都有一个最底层的核心逻辑，当我们利用机器学习思维理解线性回归的时候，首先也是要探究其底层逻辑。值得庆幸的是，虽然线性回归源于统计分析，但其算法底层逻辑和机器学习算法高度契合。 在给定的 n 个属性描述的客观事物 X = （x1,x2,x3...）中，每个 xi 都用于描述某一次观测时事物在某个维度表现出来的数值属性值。 当我们建立机器学习模型捕捉事物运行的客观规律时，本质上是希望能够综合这些维度的属性来描述事物最终运行结果，而最简单的综合这些属性的方法就是对其进行加权求和汇总，这即是线性回归的方程式表达形式： 
W 被统称为模型的参数，其中 W0 被称为截距（intercept），W1-Wn 被称为回归系数（regression conefficient），有时也是使用 β 或者 θ 来表示，其实就和我们小学时就无比熟悉的 y = ax + b 是同样的性质。其中 y 是我们的目标变量，也就是标签。Xi1 是样本 i 上的特征不同特征。 如果考虑我们有 m 个样本，则回归结果可以被写作：
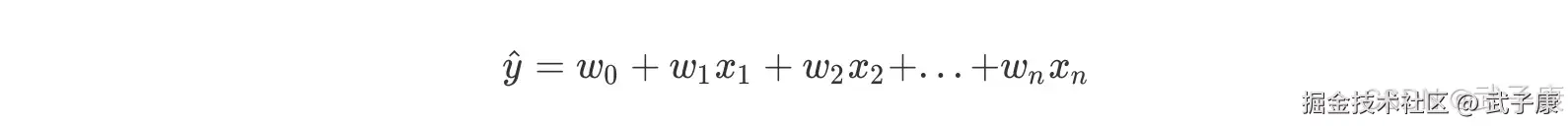其中 y 是包含了 m 个全部的样本回归结果的列向量（结构为（m,1），由于只有一列，以列的形式表示，所以叫做列向量）。注意，我们通常使用粗体的小写字母来表示向量，粗体的大写字母表示矩阵或者行列式。 我们可以使用矩阵来表示这个方程，其中 w 可以被看作是一个结构为（n+1,1）的列矩阵，X 是一个结构为（m,n+1）的特征矩阵，则有：
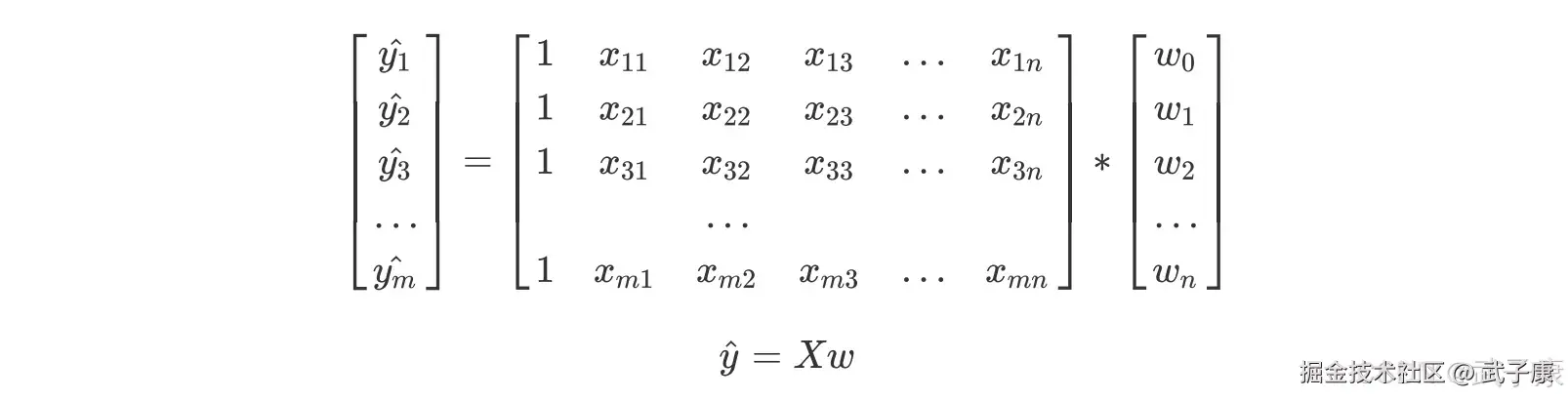线性回归的任务，就是构造一个预测函数来映射输入的特征矩阵 X 和标签值 y 的线性关系，这个预测函数在不同的教材上写法不同，可能写作 f(x)，y我（x），或者 h(x)等等形式，但无论如何，这个预测函数的本质就是我们需要构建的模型。
优化目标
对于线性回归而言，预测函数 y = Xw 就是我们的模型，在机器学习我们也称作"决策函数"。其中只有 w 是未知的，所以线性回归原理的核心就是找到模型的参数向量 w。但我们怎么才能求解呢？我们需要依赖一个概念叫：损失函数。
在之前的算法学习中，我们提到过两种模型表现：在训练集上的表现，和在测试集上的表现。我们建模，是追求模型在测试集上的表现最优，因此模型的评估指标往往是用来衡量模型在测试集上的表现的。然而，线性回归有着基于训练数据求解参数 w 的需求，并且希望训练出来模型尽可能的拟合训练数据，即模型在训练集上的预测准确率靠近 100% 越好。 因此，我们使用损失函数这个评估指标，来衡量系数为 w 的模型拟合训练集时产生的信息损失的大小，并以此衡量参数 w 的优劣。如果用一组参数建模后，模型在训练集上表现良好，那我们就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀。相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差。 即使说，我们在求解参数 w 时，追求损失函数最小，让模型在训练数据上拟合效果最优，即预测准确率尽量靠近 100%。
对于有监督的学习算法而言，建模都是依据有标签的数据集，回归类问题则是对客观事物的一个定量判别。这里以 yi 作为第 i 行数据的标签，且 yi 为连续变量，xi 为第 i 行特征所组成的向量，则线性回归建模优化方向就是希望模型判别的 yi^ 尽可能接近实际的 yi。而对于连续型变量而言，领近度度量方法可采用 SSE 来进行计算，SSE 称做【残差平方和】，也称做【误差平方和】或者【离差平方和】，因此我们优化目标可以用下述方程来表示： 
来看一个简单的例子，假设现在 w 为 [1,2] 这样的一个向量，求解出的模型：y = x1 + 2x2；
则我们的损失函数的值就是： 
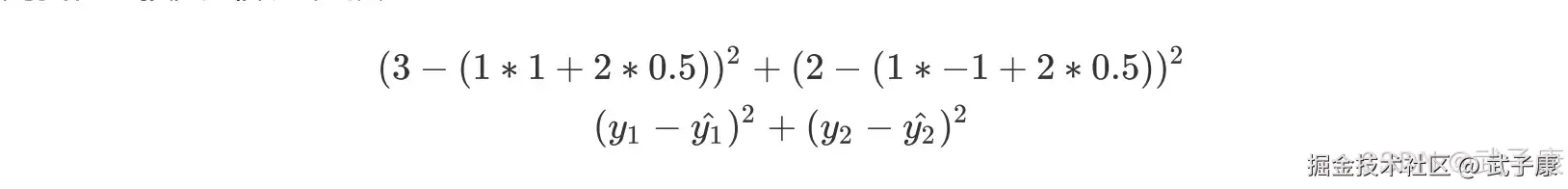
最小二乘法
现在问题转换成了求解让 SSE 最小化的参数向量 w，这种通过最小化真实值和预测值之间的 SSE来求解参数的方法叫做最小二乘法。
回顾一元线性回归的求解过程：
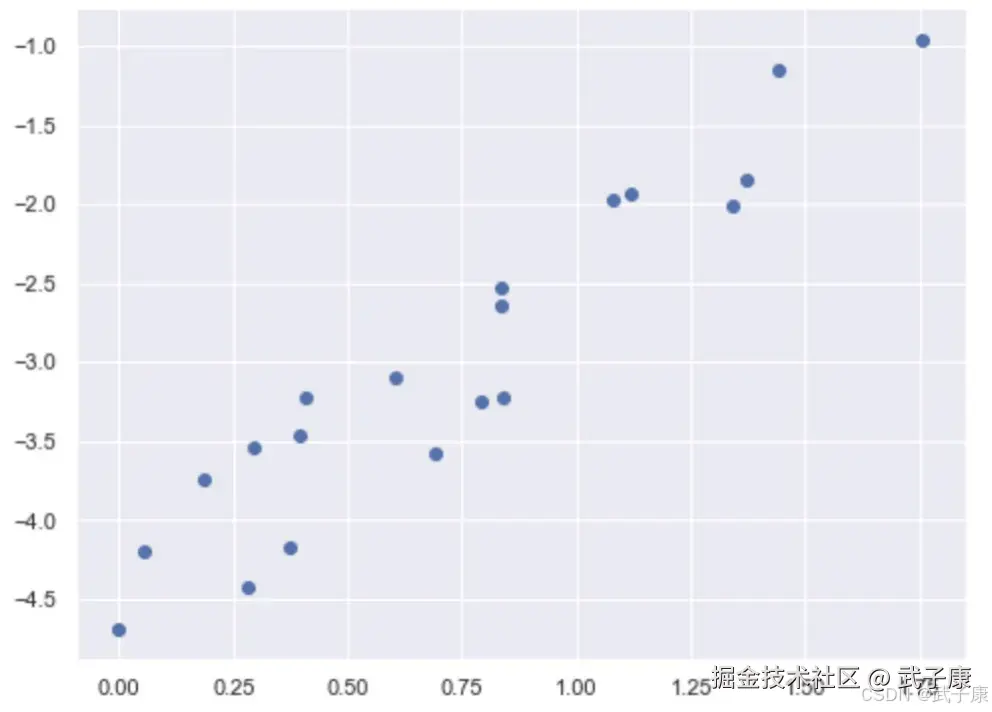对上述的数据进行拟合，可以得到： 
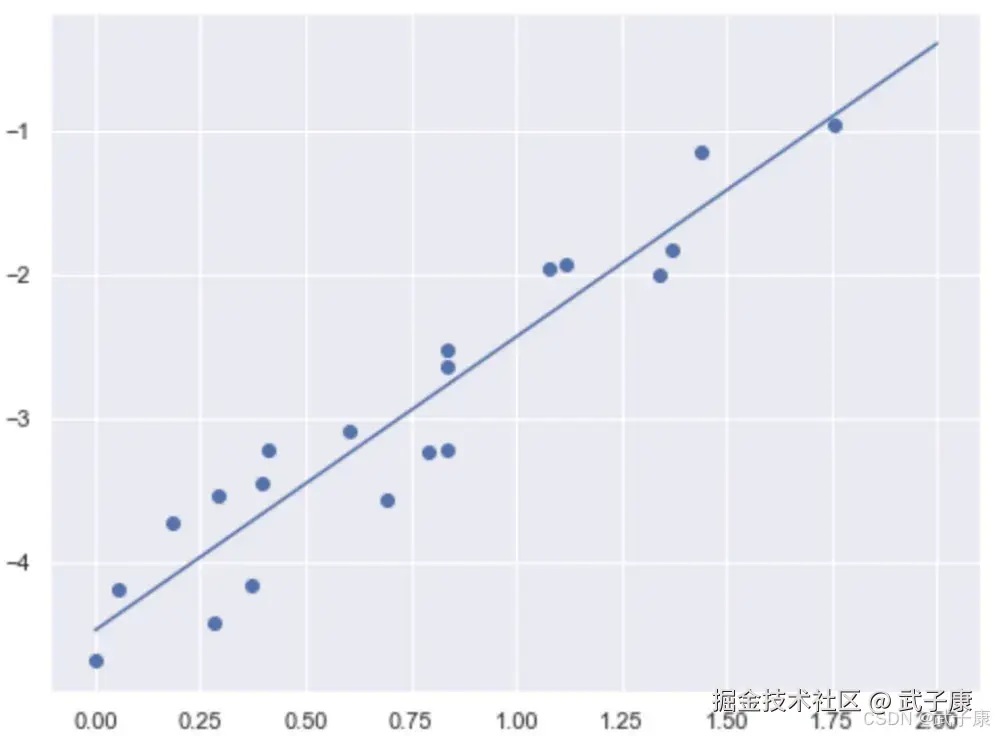假设该拟合直线为 y^ = w0 + w1x，现在我们的目标是使得该拟合直线的总的残差和达到最小，也就是最小化 SSE。 我们令该直线是以均值为核心的【均值回归】，即散点的 x 平均和 y 平均必然经过这条直线：
对于真实值 y 来说，我们可以得到：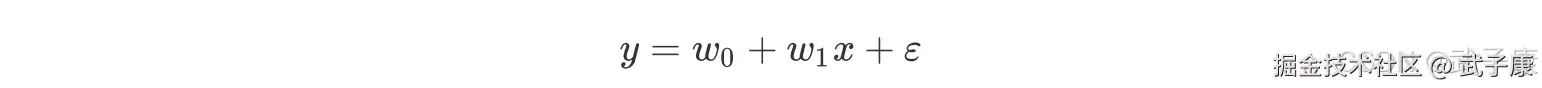 
这里 ε 为【残差】，对其进行变形，则残差平方和 SSE 为：
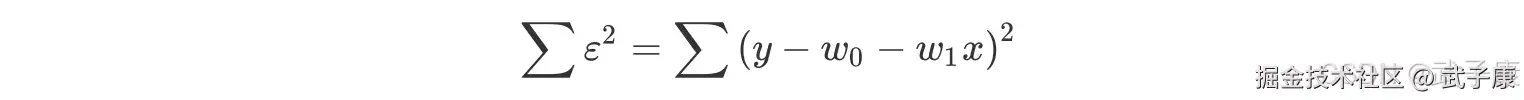要求残差平方和最小值，我们通过微积分求偏导算其极值来解决。 这里我们计算残差最小对应的参数 w1：
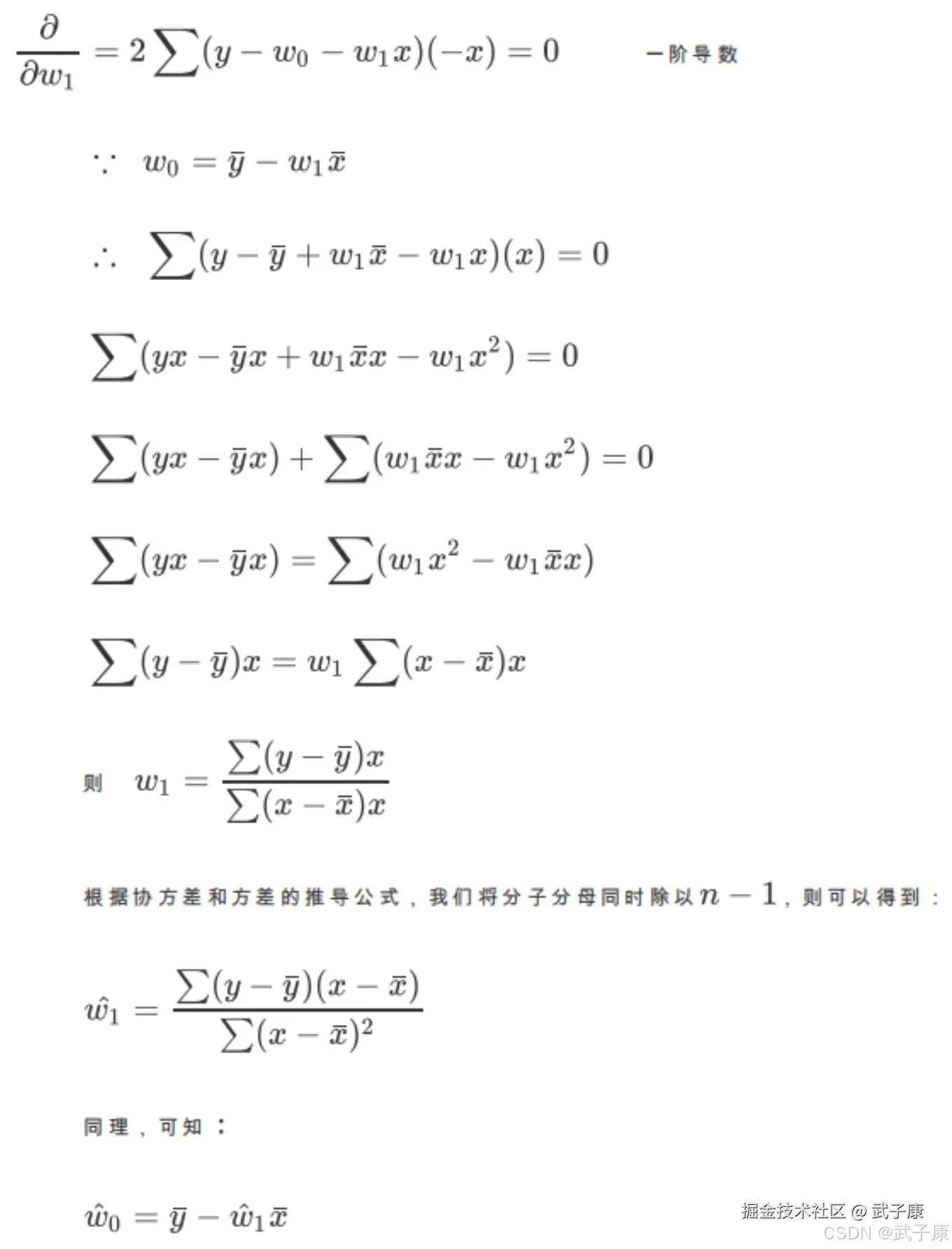
多元线性回归求解参数
更一般情况，如果我们在刚才的例子中有两列特征属性，则损失函数为：
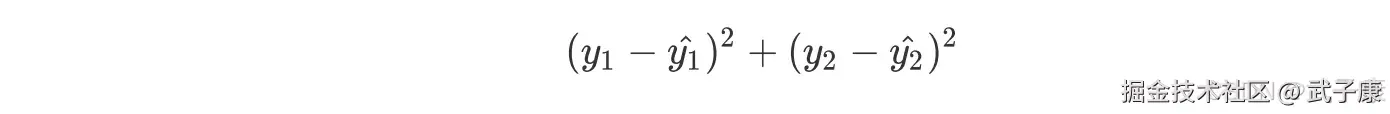这样的形式如果矩阵来表达，可以写成： 
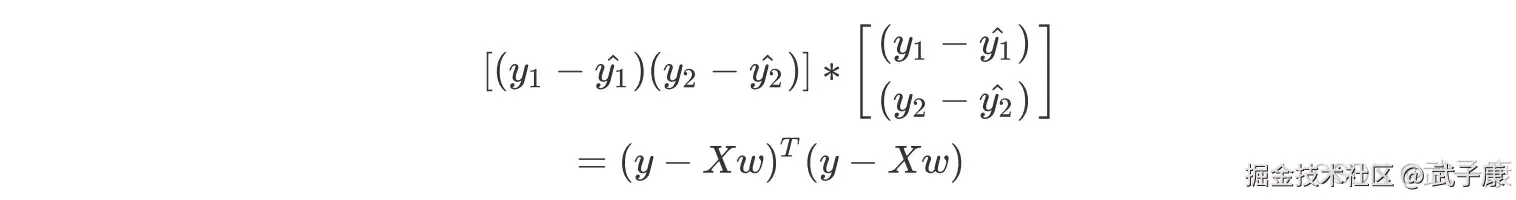矩阵相乘是对应未知元素相乘相加，就会得到和上面的式子一模一样的结果。 我们同时对 w 求偏导：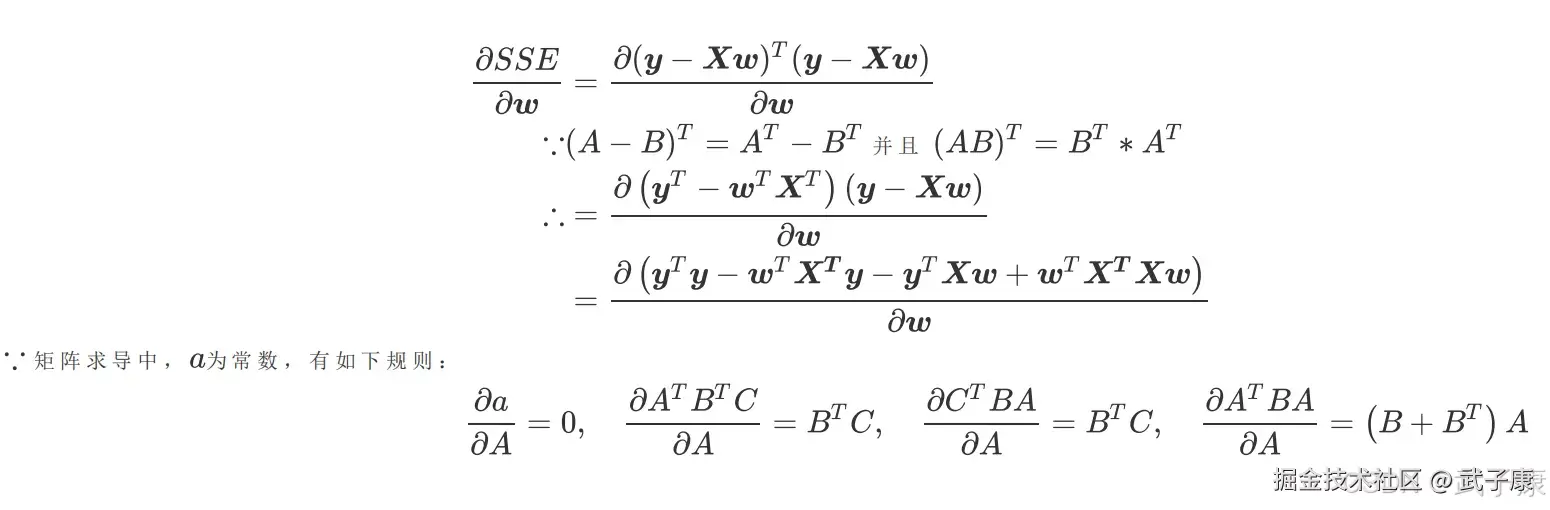 
最后得到：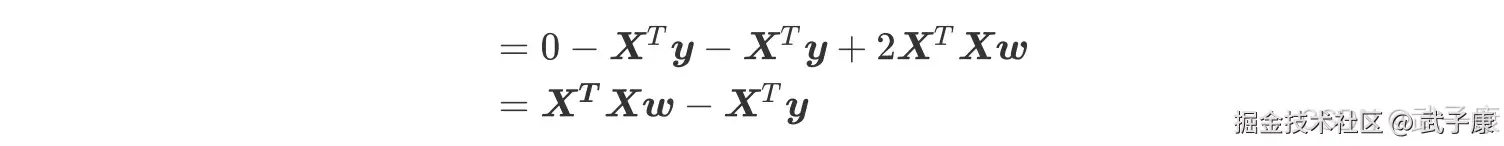 
求导后的一阶导数为 0：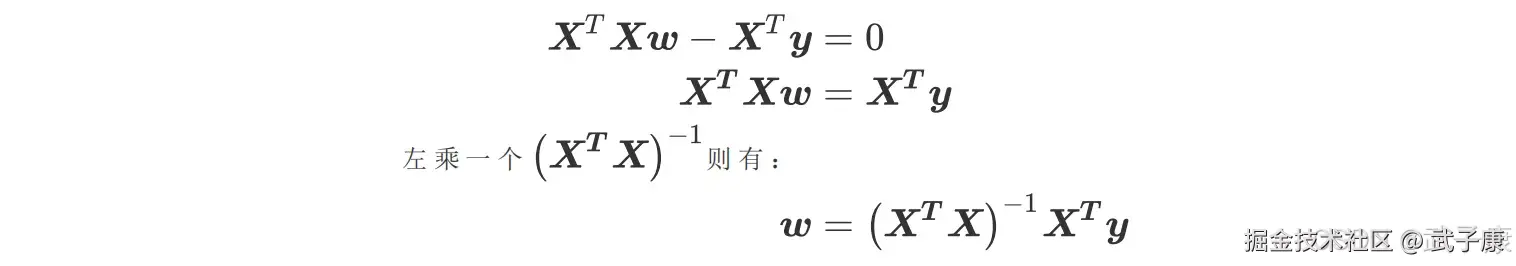 
到了这里，我们希望能够将w 留在等式的左边，其他与特征矩阵有关的部分都放到等式的右边，如此就可以求出 W 的最优解了。
错误速查
| 症状 | 根因 | 定位 | 修复 |
|---|---|---|---|
| 维度对不上：Xw 乘不出来 / 广播错误 | 未把截距并入特征（缺少全 1 列）；样本/特征维度定义不一致 | 明确 X∈ R^{m×(n+1)}、w∈ R^{(n+1)×1}、y∈ R^{m×1} | 给 X 增加 bias 列；统一符号与维度约定 |
| 解正规方程报错/不可逆：(X^TX)^{-1} 不存在 | 多重共线性、特征冗余、样本不足导致 X^TX 奇异或病态 | 看秩/条件数；检查高度相关特征；看是否 m 远小于 n | 用伪逆 pinv；做特征筛选/降维；改用岭回归（L2）稳定求解 |
| 系数巨大、符号反常、对噪声极敏感 | 特征尺度差异大；病态矩阵；异常值拉偏 | 查看特征量纲与分布；检查条件数、异常点 | 标准化/归一化；稳健回归；正则化（Ridge/Lasso） |
| 训练集拟合很好但泛化差 | 追求训练 SSE 极小导致过拟合；特征过多 | 对比训练/测试误差；交叉验证 | 降低模型复杂度；正则化；增加数据；合理划分验证集 |
| 损失数值"很大/很小"难解释 | SSE 随样本量与尺度增长；与 MSE/RMSE不可直接对比 | 看是否使用 SSE 而非 MSE/RMSE；样本量变化 | 报告 MSE/RMSE/MAE；对比时统一指标与数据尺度 |
| 推导步骤正确但实现结果不一致 | 推导假设与实现不一致：是否中心化、是否包含截距、是否用矩阵形式一次性求解 | 对齐：是否加 bias、是否做中心化/标准化、损失定义是否一致 | 固化实现约定：bias/标准化/损失；用同一公式链路复现 |
其他系列
🚀 AI篇持续更新中（长期更新）
AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架 私有部署 测试上手 架构研究 ，持续打造实用AI工具指南！ AI研究-132 Java 生态前沿 2025：Spring、Quarkus、GraalVM、CRaC 与云原生落地
💻 Java篇持续更新中（长期更新）
Java-218 RocketMQ Java API 实战：同步/异步 Producer 与 Pull/Push Consumer MyBatis 已完结，Spring 已完结，Nginx已完结，Tomcat已完结，分布式服务已完结，Dubbo已完结，MySQL已完结，MongoDB已完结，Neo4j已完结，FastDFS 已完结，OSS已完结，GuavaCache已完结，EVCache已完结，RabbitMQ已完结，RocketMQ正在更新... 深入浅出助你打牢基础！
📊 大数据板块已完成多项干货更新（300篇）：
包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！ 大数据-278 Spark MLib - 基础介绍 机器学习算法 梯度提升树 GBDT案例 详解