一、简介
为了实现机器人能够高精度的抓取,或者按照工件外轮廓形状,走特定的轨迹,需要进行一系列的标定工作;具体标定流程可以分为以下四步:
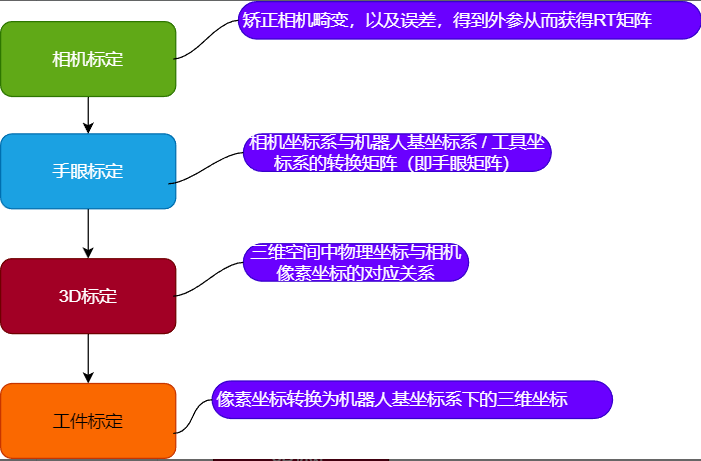
二、标定流程
1、前期准备
本文中使用2D相机为海康相机:MV-CS050-10UM
(1)、确定好棋盘格标定板的尺寸(棋盘格方格边长、标定板尺寸);
(2)、保证机器人现场各项硬件设备均正常运行,设备包括(2d相机、3D相机、相机硬件连接线,网络,相机软件,标定板等);
(3)、根据相机情况,以及实际拍照距离,调整合适的光圈(光圈越大,拍照景深越浅,反之则相反 ),将棋盘格放置到视野范围内,相机连接到MVS软件中,调整焦距直至看到棋盘格的焦点,如下图,这里相机镜头为16mm C 口定焦工业镜头, 物距为40cm左右:

2、开始标定
步骤1:相机标定(矫正相机畸变,求解内外参)
注意:这里采用的眼在手上,相机装在机械臂末端上,眼在手外时,固定相机,标定板装到机械臂末端上,移动标定板;
(1)、固定标定板 (12*9,单格6mm)整个标定过程中不能动 ,调整相机位置,确保标定板完整出现在相机视野中且图像清晰。

(2)、控制机器人多角度移动相机,**采集 15-20 张不同姿态的标定板图像以及模态姿态坐标(姿态覆盖平移、旋转、倾斜,避免图像重复,姿态尽量变化大)**尽量将标定板置为在视野上下左右,以及四个角,中间等位置;
bash
//末端位姿数据X,Y,Z,Rx,Ry,Rz
1051.6, -516.6, 960.6, -53.6, 86.7, -127.2
997.5, -457.8, 960.6, -69.8, 86.7, -127.2
1240.6,, -457.8, 1047.9, -172.2, 66.8, -24.2
1122.8, -721.5, 980.6, -130.8, 77.8, -37
1134.2, -362.3, 980.2, -149.4, 84.9, -56.9
1426.7, -668.6, 1079.8, 178.1, 56.6, 13.8
1356.6, -423.7, 1052.5, 127.4, 53.9, 49.8
1473.0, -210.4, 967.6, 87.7, 5.6, 84.1
1115.7, -812.7, 959.3, -77.2, 46.5, -91.4
1416.6, -399.0, 1075.6, 136.3, 51.9, 47.4
1486.6, -450.2, 1107.2, 117.3, 14.7, 85.9
1528.8, -236.0, 961.5, 91.3, 6.6, 83.0
1537.3, -211.8, 950.4, 88.4, 6.7, 83.5
1123.2, -870.6, 935.2, -87.2, 30.5, -92.1
1333.6, -416.3, 1070.4, 135.7, 53.8, 53.3
1422.5, -205.8, 978.9, 98.1, 27.0, 78.3
1494.0, -186.1, 998.6, 91.7, 6, 92.9
1118.6, -718.9, 953.0, -84.8, 55.2, -91.7(3)、相机软件中要清楚看到标定板的角点,计算相机的内参矩阵(焦距、主点坐标)和畸变系数(径向 + 切向畸变);
(4)、验证标定结果:用标定后的参数矫正一张测试图像,观察直线是否无畸变,角点检测误差是否在允许范围内(一般≤0.5 像素);
(5)、保存相机内参和畸变系数,外参;
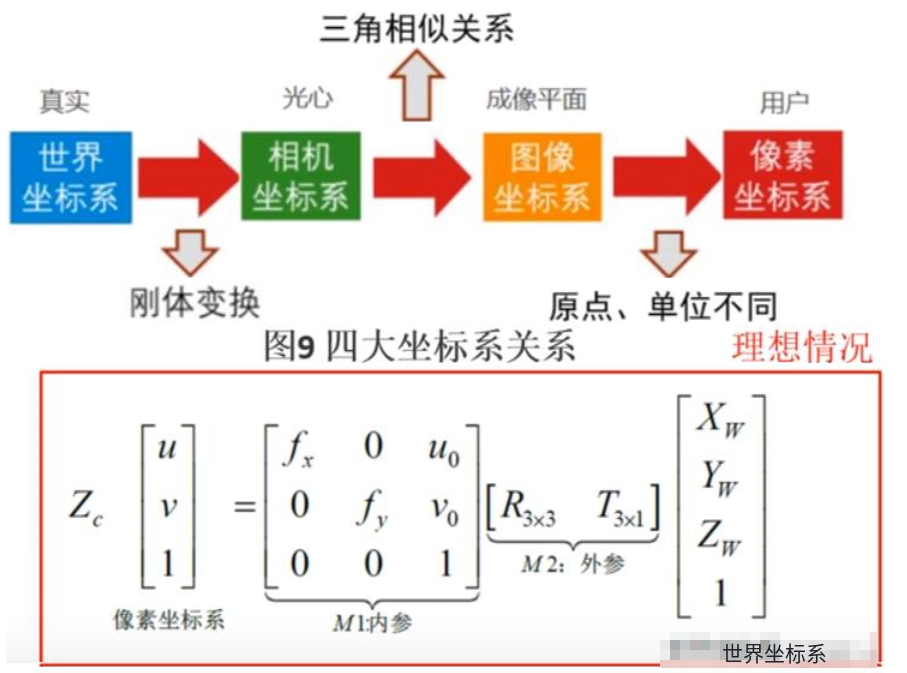
(6)、坐标系关系介绍:

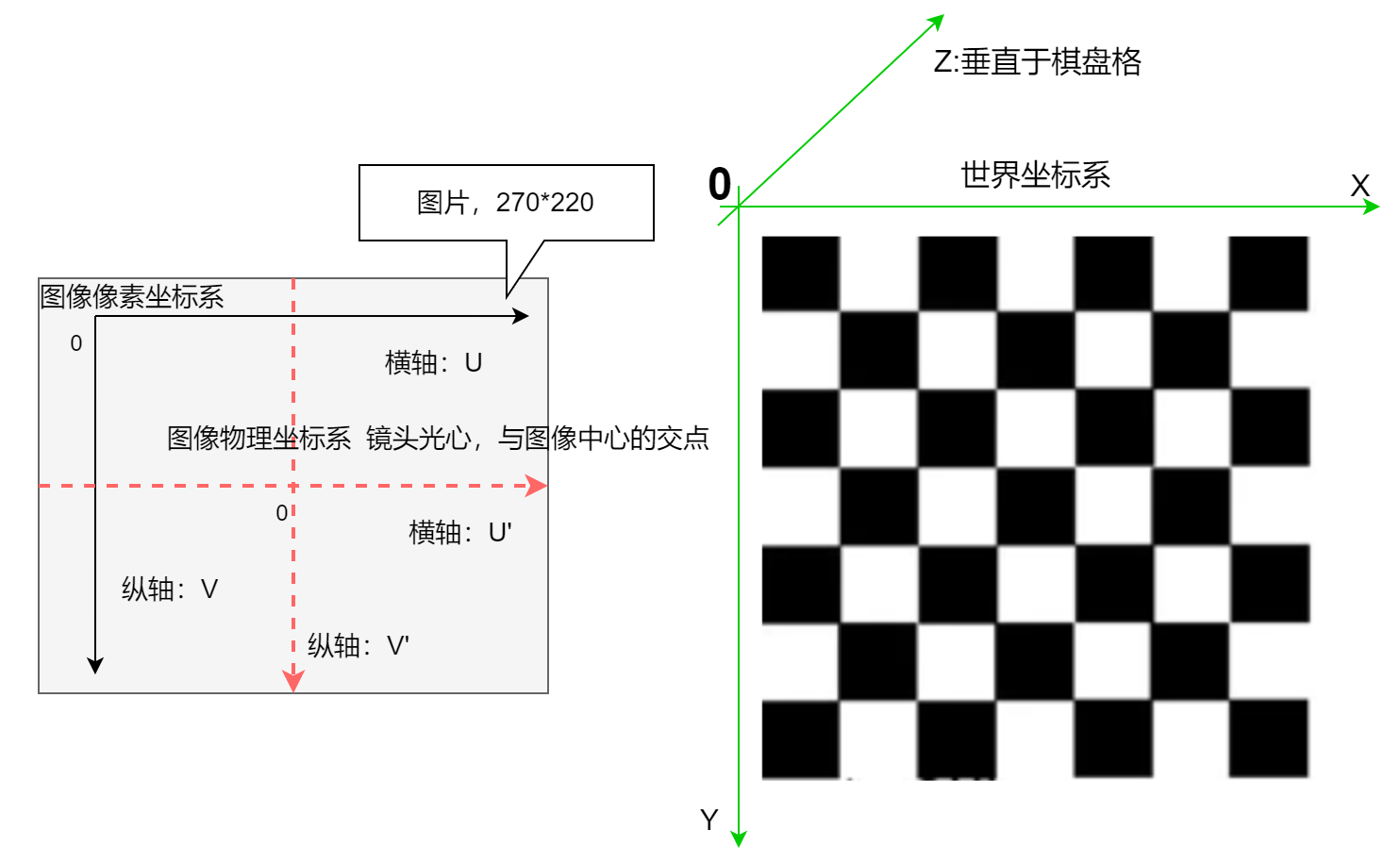
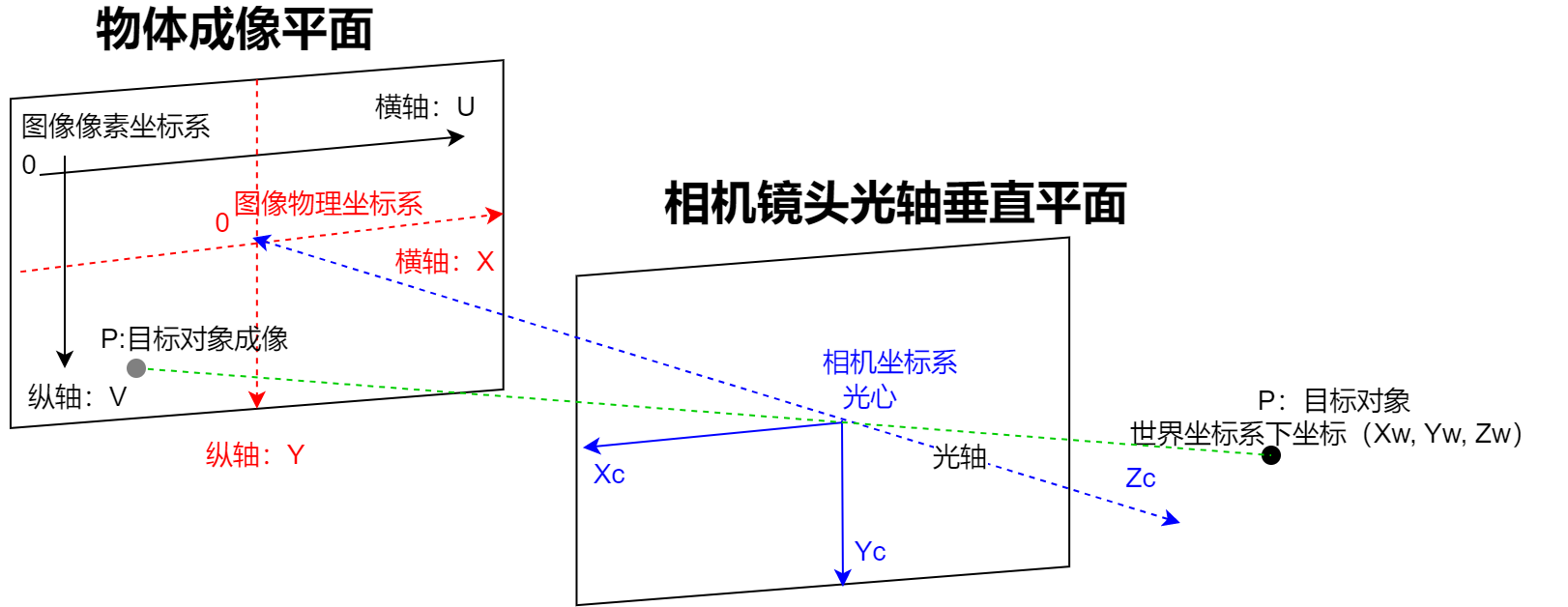
坐标系转换关系:
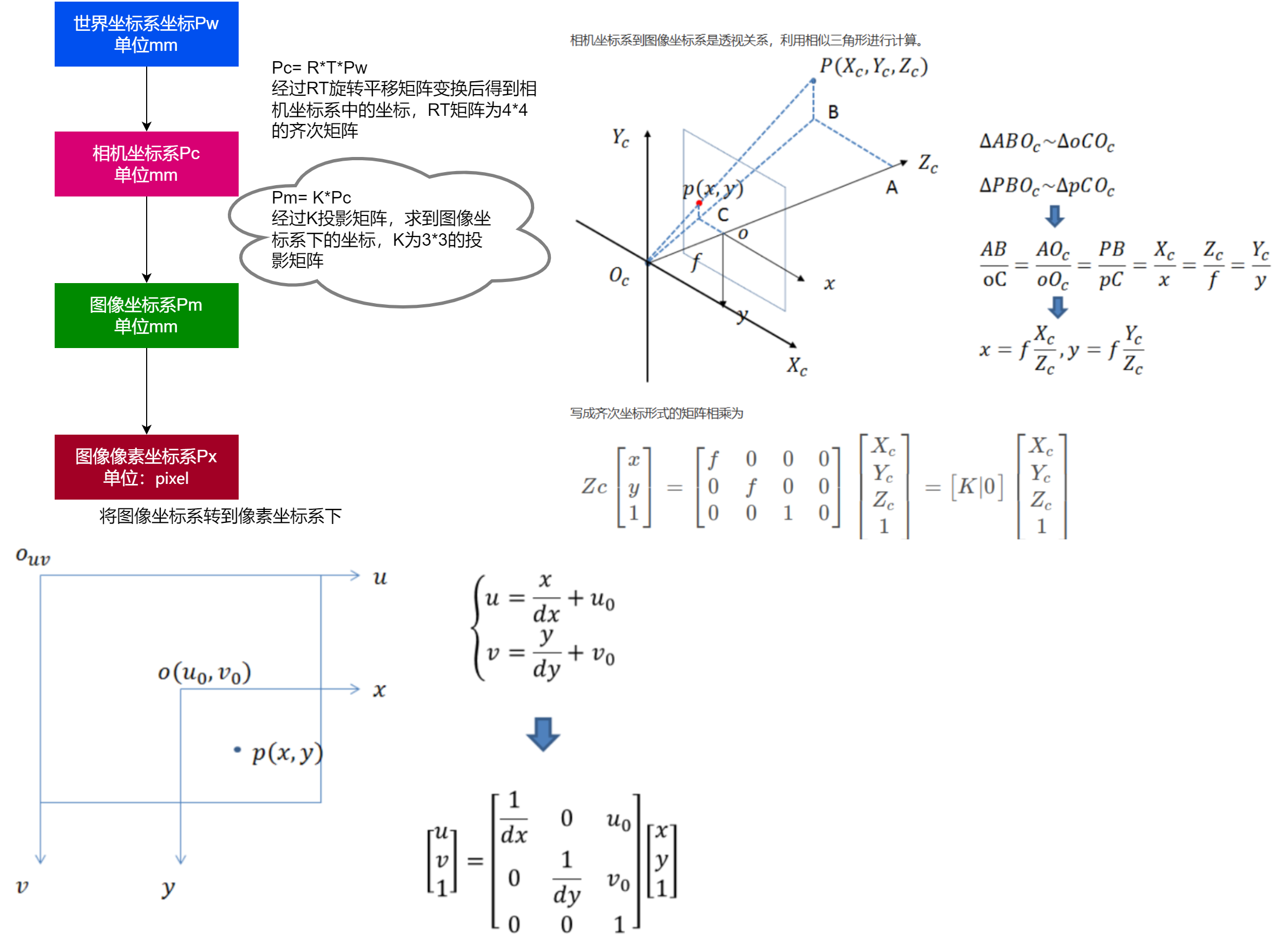
f:表示焦距;
dx: 每一像素代表多少毫米;
u0:表示图片中心点的u轴像素;
v0:表示图片中心点的v轴像素;

核心代码:
cpp
std::vector<cv::Mat> EyeInHandCal::Cam_Calibration_Corner(std::vector<cv::Mat> images, // 采集的图片数据
cv::Size board_size, // 棋盘格纵横向角点数
cv::Size2f square_size, // 棋盘格单格格的尺寸
std::string filename )// 结果存放文件
{
std::vector<std::vector<cv::Point2f>> image_points_seq;
int image_count = 0;
cv::Size image_size(0,0); // 图像尺寸
for (int i = 0; i < images.size(); i++)
{
image_count++;
cv::Mat imageInput = images[i];
if (image_count == 1)
{
image_size.width = imageInput.cols;
image_size.height = imageInput.rows;
}
std::vector<cv::Point2f> image_points_buf;
// 1. 粗检测棋盘格内角点
if (false == findChessboardCorners(imageInput, board_size, image_points_buf))
{
std::cout << "None " << i << "find the corners in the image!" << std::endl;
}
else
{
// 角点检测到,
// 2、亚像素级细化角点坐标(提升标定精度的核心操作)
// 像素级角点精度不足以支撑高精度相机标定,亚像素细化能显著降低重投影误差,提升标定精度。
cv::cornerSubPix(imageInput, // 输入图像
image_points_buf, // 输入输出:粗检测角点 → 细化后角点
cv::Size(5, 5), // 搜索窗口大小
cv::Size(-1, -1), // 死区大小(-1表示无死区)
// 迭代终止条件:迭代次数30次 或 精度0.01像素
cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::COUNT, 30, 0.01)
);
image_points_seq.push_back(image_points_buf);
}
}
//以下是摄像机标定
std::vector<std::vector<cv::Point3f>> object_points; // 所有图像对应的3D坐标集合
/* 初始化标定板上角点的三维坐标 */
int i = 0, j = 0, t = 0;
for (t = 0; t < image_points_seq.size(); t++) // 遍历所有图片数据
{
std::vector<cv::Point3f> tempPointSet; // 单张图像的3D坐标集合
for (i = 0; i < board_size.height; i++) // 遍历棋盘格的行
{
for (j = 0; j < board_size.width; j++) // 遍历棋盘格的列
{
cv::Point3f realPoint(0, 0, 0);// 计算每个角点的3D坐标:基于单个格子的物理尺寸
realPoint.x = i * square_size.width; // X轴坐标
realPoint.y = j * square_size.height; // Y轴坐标
realPoint.z = 0; // 棋盘格在XY平面,Z=0
tempPointSet.push_back(realPoint);
}
}
object_points.push_back(tempPointSet);
}
/*内外参数*/
cv::Mat cameraMatrix = cv::Mat(3, 3, CV_32FC1, cv::Scalar::all(0));// 内参矩阵(3x3)
cv::Mat distCoeffs = cv::Mat(1, 5, CV_32FC1, cv::Scalar::all(0));// 畸变系数(1x5)
std::vector<cv::Mat> tvecsMat;// 平移向量集合(每张图像一个 3x1 向量)
std::vector<cv::Mat> rvecsMat;// 旋转向量集合(每张图像一个 3x1 向量)
/* 开始标定 */
// 重投影误差(像素):评估标定精度的核心指标,越小越好(理想值 < 1 像素)
double rmsproj = cv::calibrateCamera(
object_points,// 输入:所有图像的3D世界坐标
image_points_seq,// 输入:所有图像的2D图像坐标
image_size,// 输入:图像尺寸
cameraMatrix,// 输出:内参矩阵
distCoeffs,// 输出:畸变系数
rvecsMat,// 输出:旋转向量(外参)
tvecsMat);// 输出:平移向量(外参)
std::cout << "camera the reprojection error is:" << rmsproj << std::endl;
std::cout << "camera calibration complete!\n";
// 相机内参和畸变系数是相机固有属性,一旦标定完成,可重复使用(除非相机硬件改动)
std::string camPathStr = filename + "/cam_calibration.yml";
fs::path rel_path(camPathStr);
fs::path abs_path = fs::absolute(rel_path); // 转换为绝对路径
std::string abs_path_str = abs_path.string();
cv::FileStorage fs(abs_path_str, cv::FileStorage::WRITE);
if (fs.isOpened())
{
fs << "camera_matrix" << cameraMatrix; // 写入内参矩阵
fs << "dist_coeffs" << distCoeffs;// 写入畸变系数
fs.release();
}
// 将外参转换为 4×4 齐次变换矩阵,返回结果
std::vector<cv::Mat> Pose_cam_board; // 存储所有图像的4x4位姿矩阵
for (i = 0; i < rvecsMat.size(); i++)
{
cv::Mat rot;
// 1. 罗德里格斯变换:旋转向量(3x1)→ 旋转矩阵(3x3)
cv::Rodrigues(rvecsMat[i], rot);
// 每张图片下的,平移分量
const double* tvec_data = tvecsMat[i].ptr<double>(0);
// 2. 构造4x4齐次变换矩阵 「标定板坐标系(世界坐标系) → 相机坐标系」的刚性变换
// 矩阵格式:[R | T]
// [0 | 1]
cv::Mat RT = (cv::Mat_<double>(4, 4) <<
rot.at<double>(0, 0), rot.at<double>(0, 1), rot.at<double>(0, 2), tvec_data[0],
rot.at<double>(1, 0), rot.at<double>(1, 1), rot.at<double>(1, 2), tvec_data[1],
rot.at<double>(2, 0), rot.at<double>(2, 1), rot.at<double>(2, 2), tvec_data[2],
0, 0, 0, 1);// 齐次矩阵最后一行固定为 [0,0,0,1]
Pose_cam_board.push_back(RT);
}
return Pose_cam_board;
}步骤2:手眼标定(建立相机与机器人坐标系映射)
根据机器人位姿数据和图像中标定板的位姿,计算相机坐标系相对于机器人工具坐标系的转换矩阵(手眼矩阵)。
控制机器人移动到任意未参与标定的位姿,通过手眼矩阵计算标定板在机器人基坐标系中的位置,与实际测量值对比,误差需满足项目要求(如≤0.1mm)。
情况1、眼在手上的标定方式:
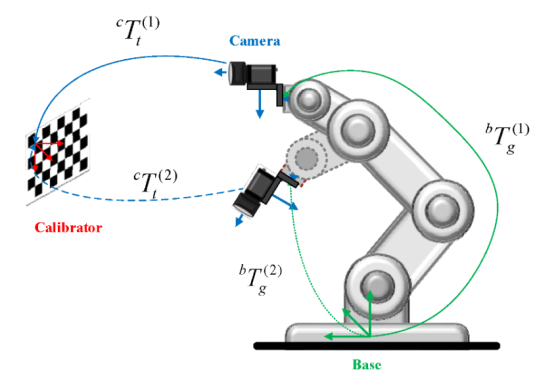
标定板上的点到机器人基座的标定关系下:
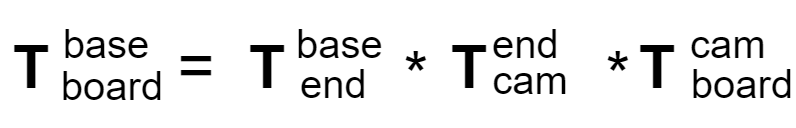
眼在手上在整个标定过程中,有两组变量是固定的,标定板到机器人基底是固定的、相机到机器人末端的关系是固定的,因此每组数据转换满足下面规则:
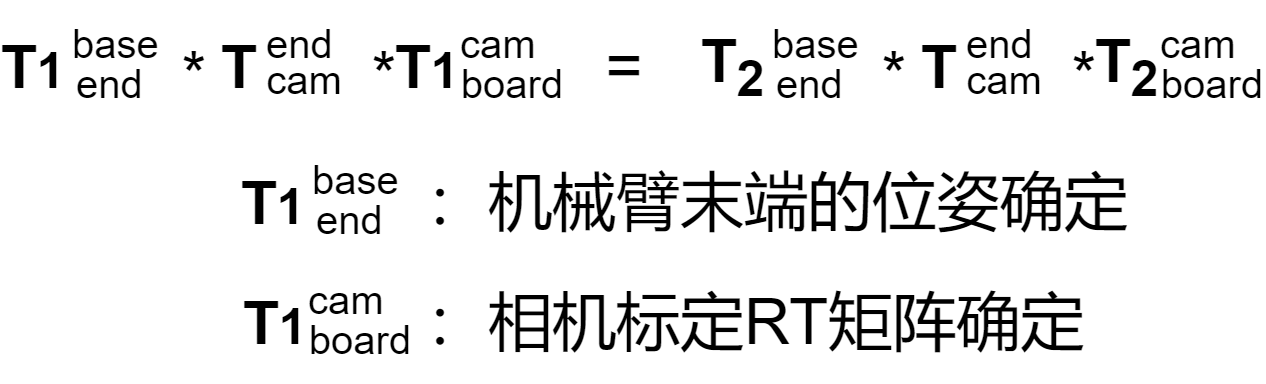
这里只需要求得矩阵,这是个定值:

核心代码:
cpp
// 拆解矩阵
void EyeInHandCal::HomogeneousMtr2RT(cv::Mat& HomoMtr, cv::Mat& R, cv::Mat& T)
{
cv::Rect R_rect(0, 0, 3, 3);
cv::Rect T_rect(3, 0, 1, 3);
R = HomoMtr(R_rect);
T = HomoMtr(T_rect);
}
// 拼接手眼矩阵
cv::Mat EyeInHandCal::R_T2HomogeneousMatrix(const cv::Mat& R, const cv::Mat& T)
{
cv::Mat HomoMtr;
cv::Mat_<double> R1 = (cv::Mat_<double>(4, 3) <<
R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2),
R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2),
R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2),
0, 0, 0);
cv::Mat_<double> T1 = (cv::Mat_<double>(4, 1) <<
T.at<double>(0, 0),
T.at<double>(1, 0),
T.at<double>(2, 0),
1);
cv::hconcat(R1, T1, HomoMtr);//矩阵拼接
return HomoMtr;
}
// 手眼标定
cv::Mat EyeInHandCal::Calibrate_HandEye(std::vector<cv::Mat> Pose_cam_board,
std::vector<cv::Mat> Pose_tool, std::string& filename)
{
//数据声明
// 机器人工具→基坐标系:旋转矩阵(3x3)和平移向量(3x1)的集合
std::vector<cv::Mat> R_gripper2base;
std::vector<cv::Mat> T_gripper2base;
// 标定板→相机坐标系:旋转矩阵(3x3)和平移向量(3x1)的集合
std::vector<cv::Mat> R_target2cam;
std::vector<cv::Mat> T_target2cam;
// 相机→机器人工具坐标系:最终求解的旋转矩阵(3x3)和平移向量(3x1)
cv::Mat R_cam2gripper = cv::Mat(3, 3, CV_64FC1);
cv::Mat T_cam2gripper = cv::Mat(3, 1, CV_64FC1);
// 相机→机器人工具坐标系:齐次变换矩阵(4x4,由旋转矩阵+平移向量组合而成)
cv::Mat Homo_cam2gripper;
// 齐次变换矩阵缓存(输入参数的备份)
std::vector<cv::Mat> Homo_target2cam;
std::vector<cv::Mat> Homo_gripper2base;
cv::Mat tempR, tempT, temp;
//计算标定板与相机间的齐次矩阵(旋转矩阵与平移向量)
for (int i = 0; i < Pose_cam_board.size(); i++)
{
temp = Pose_cam_board[i];
Homo_target2cam.push_back(temp);
//齐次转rt 4x4 齐次矩阵 → 3x3 旋转矩阵 + 3x1 平移向量
HomogeneousMtr2RT(temp, tempR, tempT);
R_target2cam.push_back(tempR);
T_target2cam.push_back(tempT);
}
for (int j = 0; j < Pose_tool.size(); j++)
{
temp = Pose_tool[j];
Homo_gripper2base.push_back(temp);
HomogeneousMtr2RT(temp, tempR, tempT);
R_gripper2base.push_back(tempR);
T_gripper2base.push_back(tempT);
}
////TSAI计算速度最快(试一下标定方法)
cv::calibrateHandEye(R_gripper2base, T_gripper2base, R_target2cam, T_target2cam, R_cam2gripper, T_cam2gripper, cv::CALIB_HAND_EYE_TSAI);
Homo_cam2gripper = R_T2HomogeneousMatrix(R_cam2gripper, T_cam2gripper);
std::cout << "Hand-eye matrix (eye on hand)" << Homo_cam2gripper << std::endl;
std::string handEyePathStr = filename + "/HandInEye_calibration.yml";
std::filesystem::path rel_path(handEyePathStr);
std::filesystem::path abs_path = fs::absolute(rel_path); // 转换为绝对路径
std::string handEyeAbs_path_str = abs_path.string();
cv::FileStorage fs1(handEyeAbs_path_str, cv::FileStorage::WRITE);
if (fs1.isOpened())
{
fs1 << "calibration_result" << Homo_cam2gripper;
fs1.release();
}
return Homo_cam2gripper;
}即为所求未知矩阵,其他矩阵都为已知值。相机内外参及手眼标定完成后,后续如果整体结构和位置未发生变化,则不再需要进行标定。
通过上述可以求得手眼矩阵为:
bash
data: [ -3.0800181771835300e-02, -3.5519725622691251e-01, 9.3428382088725859e-01, 4.7502537069954926e+01, // x = 4.7502537069954926
9.9952085943240698e-01, -1.3812516610564485e-02, 2.7699565779723656e-02, -7.0661239637111962e+01, // y = -7.0661239637111962
3.0660010313520725e-03, 9.3468931926804211e-01, 3.5545249483428831e-01, 2.0935566047297883e+02, //z = 209.35566047297883, 单位为mm
0, 0, ., 1. ]
// 有了x,y, z, 可以实际测量一下2D相机相对于机械臂末端的位置信息,从而验证标定是否正确
情况2、眼在手外的标定方式:
**整个标定过程中,相机到机器人基座的位置关系是固定的,标定板到末端也是固定的,**标定板固定在机械臂末端上,移动 15-20个不同位姿,可以获取到各个角点的的RT变化矩阵,同时根据末端位姿可以获取机器人的;
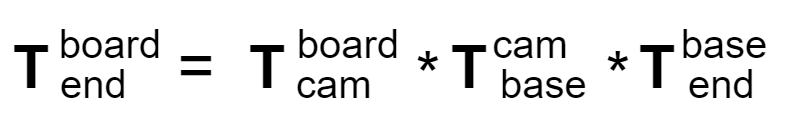
从上面的公式变换中,可以得出以下等式关系:
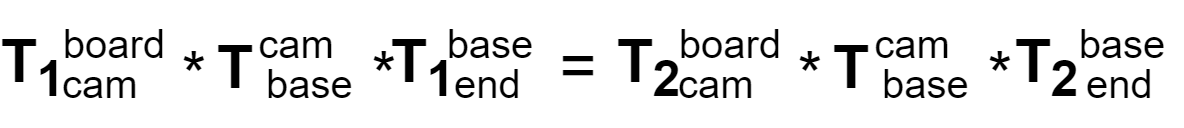
从这里不难看出只需要求出定值矩阵 :
步骤3:3D标定
前面的标定,仅仅获得了2d相机看到物体的2D信息,但是实际用机械臂,进行码垛抓取时,还需要3D的Z方向信息,因而需要3D标定;
完成相机和机械臂的标定后,开始进行工件标定。移动机械臂,在3D相机的合适成像范围内采集点云数据(本文中使用的是梅卡曼德为1m-2m,1.5m最好);
3D标定的核心目的:
(1)修正相机(采集相机)的镜头畸变;
(2)求解**「结构光投射器坐标系」与「相机坐标系」的相对位姿(外参)**,建立两者的精准映射;
(3)建立"光栅图案的相位/灰度信息"与"真实物理深度"的对应关系,生成深度查询表(LUT);
(4) 最终输出"像素坐标→3D物理坐标(X,Y,Z)"的精准转换模型;
(1)、点云位姿数据采集
在采集数据的时候,尽量采集特征点比较多的区域,方便后续的配准定位,使用3D相机拍照的同时,也要记录好机器人末端的数据;
修正相机(采集相机)的镜头畸变;
求解「结构光投射器坐标系」与「相机坐标系」的相对位姿(外参),建立两者的精准映射------>手眼矩阵;

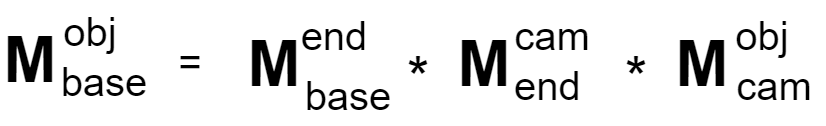
采集15-20组数据,由于整个标定过程中标定板始终固定,所以等式左边是个定值;
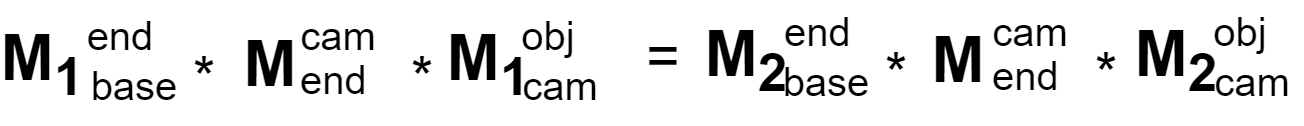
这里同理,整个标定过程中要求的定值为:
该矩阵为3D相机的手眼标定矩阵;
核心代码:
cpp
//3d相机标定 非均匀圆点标定板使用下列算法
std::vector<cv::Mat> EyeInHandCal::Cam_Calibration_Circle(std::vector<cv::Mat> images, // 输入:采集的多张标定板图像
cv::Size board_size,// 输入:标定板的圆点网格尺寸(如cv::Size(8,5)表示8列5行)
cv::Size2f square_size, // 输入:圆点中心的物理间距(单位:mm,width/x方向,height/y方向)
std::string filename)// 输入:保存标定结果的目录路径
{
std::vector<std::vector<cv::Point2f>> image_points_seq;
int image_count = 0;
cv::Size image_size;
std::vector<cv::Point2f> image_points_buf;
for (int i = 0; i < images.size(); i++)
{
image_count++;
cv::Mat imageInput = images[i];
if (image_count == 1)
{
image_size.width = imageInput.cols;
image_size.height = imageInput.rows;
}
// 初始化Blob检测器参数(针对圆点特征优化)
cv::SimpleBlobDetector::Params params;
params.thresholdStep = 10;//阈值越小检测越精确,计算速度变慢
params.filterByInertia = true;//斑点圆度的限制变量,默认是不限制 开启圆度过滤(保证只检测圆形斑点)
params.minInertiaRatio = 0.5f;// 最小圆度(0.5表示至少是"半椭圆"以上的圆形)
params.filterByColor = true; //按颜色过滤(只检测白色圆点)
params.blobColor = 255;//255表示只提取白色斑点,0表示只提取黑色斑点
params.filterByArea = true;//按面积过滤(排除过小的噪声斑点)
params.minArea = 500;// 最小斑点面积(像素)
// 创建Blob检测器,用于圆点中心提取
cv::Ptr<cv::FeatureDetector> detector = cv::SimpleBlobDetector::create(params);
// 核心:检测非均匀圆点网格的中心(CALIB_CB_ASYMMETRIC_GRID表示不对称网格)
if (false == findCirclesGrid(imageInput, board_size, image_points_buf, cv::CALIB_CB_ASYMMETRIC_GRID, detector))
{
std::cout << "No circle center detected!" << std::endl;
}
else
{
image_points_seq.push_back(image_points_buf); // 保存检测到的像素坐标
std::cout << "NO:" << i << ", image dot detection completed" << std::endl;
}
}
//以下是摄像机标定
std::vector<std::vector<cv::Point3f>> object_points;
/* 初始化标定板上角点的三维坐标 */
for (int t = 0; t < image_points_seq.size(); t++)
{
std::vector<cv::Point3f> tempPointSet;
for (int i = 0; i < board_size.height; i++)// 遍历标定板行数
{
for (int j = 0; j < board_size.width; ++j)// 遍历标定板列数
{
cv::Point3f realPoint;
// 非均匀网格的核心坐标规则:奇数行的列坐标偏移半个间距
realPoint.x = (2 * j + (i % 2)) * square_size.width;
realPoint.y = i * square_size.height;
realPoint.z = 0;// 标定板在世界坐标系的Z=0平面
tempPointSet.push_back(realPoint);
}
}
object_points.push_back(tempPointSet);// 保存每幅图像对应的世界坐标
}
// 初始化内参、畸变系数、外参存储变量
cv::Mat cameraMatrix = cv::Mat(3, 3, CV_32FC1, cv::Scalar::all(0));// 相机内参矩阵(3x3)
cv::Mat distCoeffs = cv::Mat(1, 5, CV_32FC1, cv::Scalar::all(0));// 畸变系数(k1,k2,p1,p2,k3)
std::vector<cv::Mat> tvecsMat;// 平移向量(每幅图像的相机→标定板的平移)
std::vector<cv::Mat> rvecsMat;// 旋转向量(每幅图像的相机→标定板的旋转)
/* 开始标定 */
double rmsproj = cv::calibrateCamera(
object_points,// 标定板世界坐标
image_points_seq,// 圆点像素坐标
image_size,// 图像尺寸
cameraMatrix,// 输出:相机内参矩阵
distCoeffs,// 输出:畸变系数包含径向畸变 (k1,k2,k3) 和切向畸变 (p1,p2),修正镜头畸变;
rvecsMat,// 输出:畸变系数
tvecsMat);// 输出:每幅图像的平移向量
std::cout << "Calibration complete!\n";
std::string cam3dPathStr = filename + "/cam_calibration.yml";
fs::path rel_path(cam3dPathStr);
fs::path abs_path = fs::absolute(rel_path); // 转换为绝对路径
std::string cam3d_abs_path_str = abs_path.string();
cv::FileStorage fs(cam3d_abs_path_str, cv::FileStorage::WRITE);
if (fs.isOpened())
{
fs << "camera_matrix" << cameraMatrix;
fs << "dist_coeffs" << distCoeffs;
fs.release();
}
// 将旋转向量+平移向量转换为4x4 RT矩阵(相机→标定板的位姿)
std::vector<cv::Mat> Pose_cam_board;
for (i = 0; i < rvecsMat.size(); i++)
{
cv::Mat rot;
cv::Rodrigues(rvecsMat[i], rot);// 旋转向量→旋转矩阵(3x3)
// 构建4x4齐次变换矩阵(RT)
cv::Mat RT = (cv::Mat_<double>(4, 4) << rot.at<double>(0, 0), rot.at<double>(0, 1), rot.at<double>(0, 2), tvec_data[0],
rot.at<double>(1, 0), rot.at<double>(1, 1), rot.at<double>(1, 2), tvec_data[1],
rot.at<double>(2, 0), rot.at<double>(2, 1), rot.at<double>(2, 2), tvec_data[2],
0, 0, 0, 1);
Pose_cam_board.push_back(RT);
}
return Pose_cam_board;
}(2)、手眼标定
这里手眼标定逻辑跟2D一致
步骤4、工件标定
用3D相机采集工件数据,尽量集中在特征点较多的区域,采集到的点云数据为待配准点云数据,模型文件作为目标点云数据,进行点云配准(fpfh),描述点云局部结构,步骤如下所示:
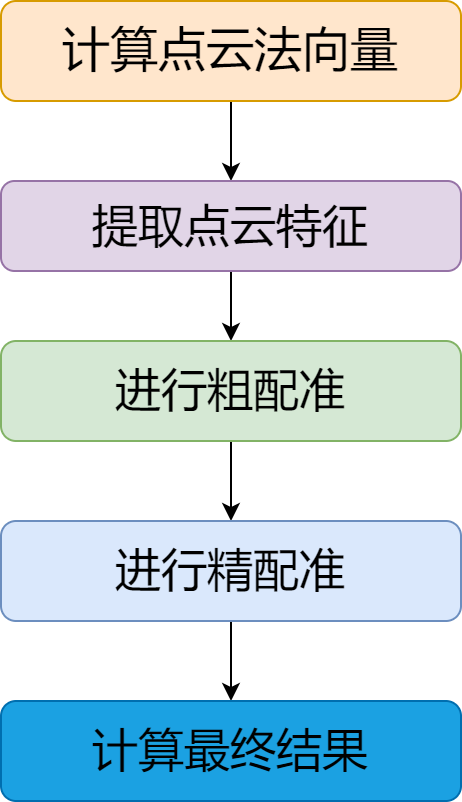
点云配准目的是得到,3D相机与产品点云的转化关系矩阵;
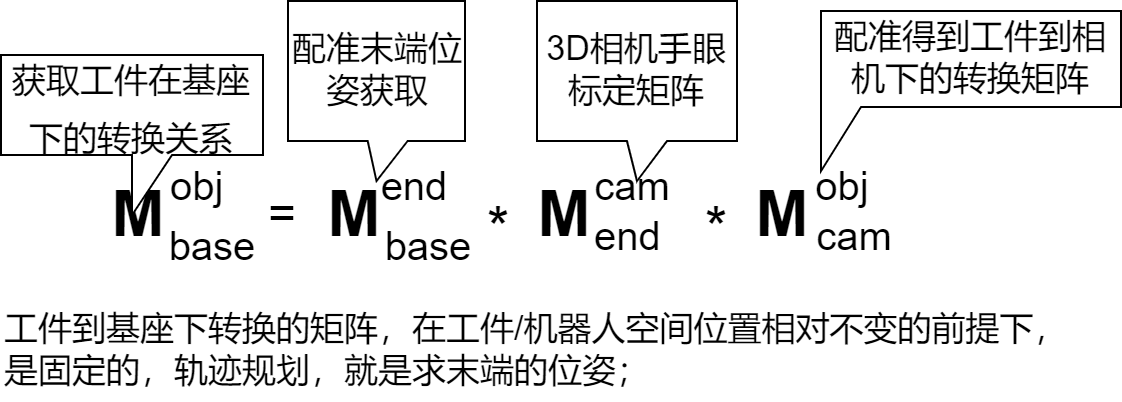
点云配准后得到的矩阵,就是工件在3D相机下的变换关系;因为标定中末端位姿是确定的,因而满足以下转换:
核心代码:
cpp
// 计算点云法向量
// 计算每个点的法向量(描述点云表面的朝向),是 FPFH 特征提取的必要前提。
pcl::PointCloud<pcl::Normal>::Ptr Registration::computeNormals(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud,
int k, bool rever)
{
pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);
// 多线程法向量估计(NormalEstimationOMP比普通版快)
pcl::NormalEstimationOMP<pcl::PointXYZ, pcl::Normal> norm_omp;
norm_omp.setInputCloud(cloud); // 输入点云
norm_omp.setSearchMethod(tree); // 用KdTree加速邻域搜索
norm_omp.setKSearch(k); // 取每个点的k个近邻计算法向量(k=10)
norm_omp.setNumberOfThreads(8); // 8线程加速
norm_omp.compute(*normals); // 计算法向量
if (rever){ // 反转法向量方向(解决法向量朝向不一致的问题)
for (auto& n : normals->points)
{
n.normal_x *= -1.0f;
n.normal_y *= -1.0f;
n.normal_z *= -1.0f;
}
}
return normals;
}
//提取点云特征
pcl::PointCloud<pcl::FPFHSignature33>::Ptr Registration::computeFpfhWithNormals(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud,
const pcl::PointCloud<pcl::Normal>::Ptr& normals, int k)
{
pcl::PointCloud<pcl::FPFHSignature33>::Ptr fpfh(new pcl::PointCloud<pcl::FPFHSignature33>);
// 多线程FPFH特征估计
pcl::FPFHEstimationOMP<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh_est;
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree_fpfh(new pcl::search::KdTree<pcl::PointXYZ>);
fpfh_est.setNumberOfThreads(8);
fpfh_est.setInputCloud(cloud); // 输入点云
fpfh_est.setInputNormals(normals); // 输入法向量
fpfh_est.setSearchMethod(tree_fpfh); // KdTree加速
fpfh_est.setKSearch(k); // num必须大于等于k, 取k个近邻计算特征(k=10)
fpfh_est.compute(*fpfh); // 输出33维FPFH特征
return fpfh;
}
Eigen::Matrix4f Registration::registration(const std::string& model_path,
const std::string& cloud_path)
{
pcl::PointCloud<pcl::PointXYZ>::Ptr target_cloud(new pcl::PointCloud<pcl::PointXYZ>);
if (pcl::io::loadPLYFile<pcl::PointXYZ>(model_path, *target_cloud) == -1)
{
std::cout << "Failed to load the model point cloud file!" << std::endl;
}
pcl::PointCloud<pcl::PointXYZ>::Ptr source_cloud(new pcl::PointCloud<pcl::PointXYZ>);
if (pcl::io::loadPLYFile<pcl::PointXYZ>(cloud_path, *source_cloud) == -1)
{
std::cout << "Failed to load camera point cloud file!" << std::endl;
}
//点云滤波
/*pcl::PointCloud<pcl::PointXYZ>::Ptr target_cloud_filtered = voxelFilter(target_cloud, 0.05);
pcl::PointCloud<pcl::PointXYZ>::Ptr source_cloud_filtered = voxelFilter(source_cloud, 0.05);*/
//计算点云法线
// 计算法向量(目标点云不反转,源点云反转)
pcl::PointCloud<pcl::Normal>::Ptr target_cloud_normals = computeNormals(target_cloud, 10);
pcl::PointCloud<pcl::Normal>::Ptr source_cloud_normals = computeNormals(source_cloud, 10, true);
// 提取FPFH特征
pcl::PointCloud<pcl::FPFHSignature33>::Ptr target_fpfh = computeFpfhWithNormals(target_cloud, target_cloud_normals, 10);
pcl::PointCloud<pcl::FPFHSignature33>::Ptr source_fpfh = computeFpfhWithNormals(source_cloud, source_cloud_normals, 10);
//粗配准
pcl::PointCloud<pcl::PointXYZ>::Ptr sac_result(new pcl::PointCloud<pcl::PointXYZ>);
//没有必要的话,参数尽量不要进行调整
pcl::SampleConsensusPrerejective<pcl::PointXYZ, pcl::PointXYZ, pcl::FPFHSignature33> sac_ia;
sac_ia.setInputSource(source_cloud);
sac_ia.setSourceFeatures(source_fpfh);
sac_ia.setInputTarget(target_cloud);
sac_ia.setTargetFeatures(target_fpfh);
// 核心参数(无需轻易调整)
sac_ia.setMaximumIterations(300); // 最大迭代次数(越多越准,越慢)
sac_ia.setNumberOfSamples(3); // 每次迭代随机采样3个点(估计变换矩阵的最小点数)
sac_ia.setCorrespondenceRandomness(5); // 每个源点取5个候选匹配点(提升鲁棒性)
sac_ia.setSimilarityThreshold(0.3f); // 法向量相似度阈值(越小匹配越严格)
sac_ia.setMaxCorrespondenceDistance(3); // 匹配点的最大空间距离(单位:米)
//sac_ia.setInlierFraction(0.25f);//内点所占最小比例
sac_ia.align(*sac_result); // 执行粗配准
Eigen::Matrix4f coarseTrans = sac_ia.getFinalTransformation(); // 粗配准变换矩阵
pcl::IterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> icp;
// 输入:粗配准后的源点云 + 目标点云
pcl::PointCloud<pcl::PointXYZ>::Ptr reg_result(new pcl::PointCloud<pcl::PointXYZ>);
////设置ICP参数
icp.setInputSource(sac_result);
icp.setInputTarget(target_cloud);
// ICP核心参数
icp.setMaximumIterations(300); // 最大迭代次数
icp.setRANSACIterations(100); // RANSAC迭代次数(剔除外点)
icp.setRANSACOutlierRejectionThreshold(0.05); // RANSAC外点剔除阈值(米)
icp.setMaxCorrespondenceDistance(3); // 匹配点最大距离(米)
icp.setTransformationEpsilon(0.0000001); // 变换矩阵的最小变化量(收敛条件)
icp.setEuclideanFitnessEpsilon(0.000001); // 点云间的最小均方误差(收敛条件)
//执行ICP
icp.align(*reg_result);
Eigen::Matrix4f transMatrix = icp.getFinalTransformation(); // 精配准变换矩阵
// 最终变换矩阵 = 精配准矩阵 * 粗配准矩阵(矩阵乘法顺序不能反!)
Eigen::Matrix4f final_matrix = transMatrix * coarseTrans;
std::cout << "The final transformation is:" << final_matrix << std::endl;
return final_matrix;
}}
三、总结
以上就是机器人标定相关的核心技术逻辑与实践要点啦。从相机标定的坐标系统一,到点云配准的变换矩阵求解,再到矩阵求逆在坐标转换中的关键作用,每一步都是实现机器人精准感知与运动控制的基石。希望这些内容能为正在深耕机器人标定领域的你提供些许参考~