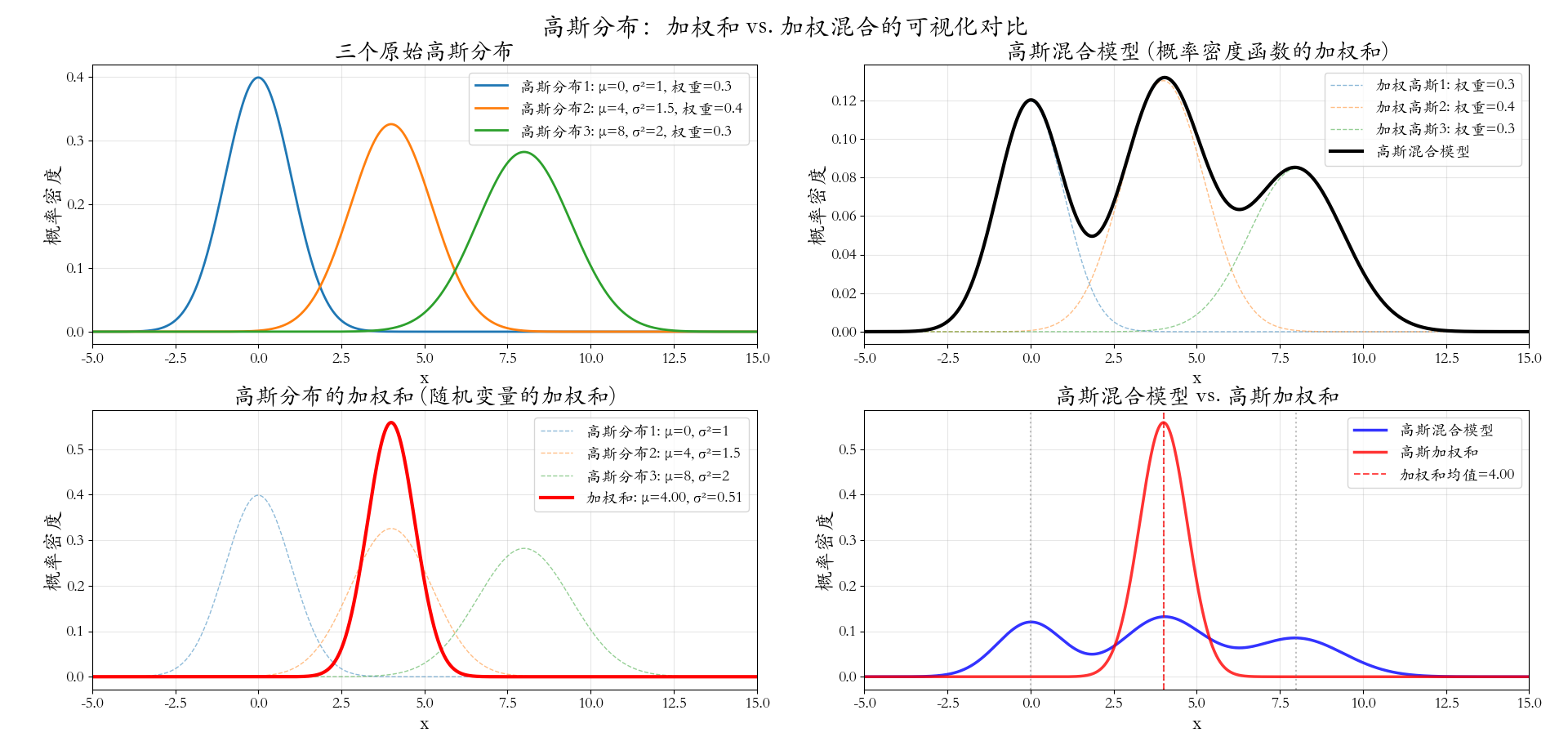
这两个概念虽然都基于高斯分布,但代表着两种完全不同的数学操作和思维方式。简单来说,高斯分布的加权和产生的是一个新的高斯分布,而高斯分布的加权混合描述的是一个复杂的多模态分布。
| 维度 | 高斯分布的加权和 | 高斯混合模型 |
|---|---|---|
| 数学本质 | 随机变量的线性组合 | 概率密度函数的凸组合 |
| 结果分布 | 仍然是高斯分布 | 通常不是高斯分布 |
| 参数计算 | 直接计算(解析解) | 迭代优化(如EM算法) |
| 可解释性 | 参数有直接物理意义 | 分量代表数据中的子群体 |
| 典型形态 | 单峰 | 多峰(可拟合复杂形状) |
| 计算复杂度 | 低(封闭形式解) | 高(需要迭代优化) |
一、高斯分布基础
高斯分布(又称正态分布)是最重要的概率分布之一,其概率密度函数呈钟形曲线:
N(x∣μ,σ2)=12πσe−(x−μ)22σ2\mathcal{N}(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}N(x∣μ,σ2)=2π σ1e−2σ2(x−μ)2
其中,μ\muμ是均值,决定了分布的中心位置;σ2\sigma^2σ2是方差,决定了分布的宽度。高斯分布之所以无处不在,很大程度上归功于中心极限定理:大量独立同分布的随机变量之和趋近于高斯分布。
二、高斯分布的加权和
核心思想 :高斯随机变量的线性组合仍然是高斯随机变量。
假设有两个独立的高斯随机变量:
X1∼N(μ1,σ12)X_1 \sim \mathcal{N}(\mu_1, \sigma_1^2)X1∼N(μ1,σ12)
X2∼N(μ2,σ22)X_2 \sim \mathcal{N}(\mu_2, \sigma_2^2)X2∼N(μ2,σ22)
它们的加权和定义为:
Y=aX1+bX2Y = aX_1 + bX_2Y=aX1+bX2
其中 aaa 和 bbb 是权重系数。根据高斯分布的性质,YYY 也是一个高斯随机变量:
Y∼N(aμ1+bμ2,a2σ12+b2σ22)Y \sim \mathcal{N}(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2)Y∼N(aμ1+bμ2,a2σ12+b2σ22)
关键特性:
- 封闭性:这是高斯分布最优雅的性质之一。无论你如何线性组合高斯随机变量,结果仍然是高斯分布。
- 参数可计算:结果分布的参数可以直接从原始分布的参数和权重计算得出,无需复杂迭代。
- 可扩展到多维 :对于多维高斯分布,类似的性质同样成立。如果 X1∼N(μ1,Σ1)X_1 \sim \mathcal{N}(\mu_1, \Sigma_1)X1∼N(μ1,Σ1) 和 X2∼N(μ2,Σ2)X_2 \sim \mathcal{N}(\mu_2, \Sigma_2)X2∼N(μ2,Σ2) 是独立的多维高斯向量,那么 Y=AX1+BX2Y = AX_1 + BX_2Y=AX1+BX2 也是一个高斯向量,其参数为:
Y∼N(Aμ1+Bμ2,AΣ1AT+BΣ2BT)Y \sim \mathcal{N}(A\mu_1 + B\mu_2, A\Sigma_1A^T + B\Sigma_2B^T)Y∼N(Aμ1+Bμ2,AΣ1AT+BΣ2BT)
这就像是调配一种新的颜色:
- 红色油漆(高斯分布1)
- 蓝色油漆(高斯分布2)
- 按比例混合后,你得到一种全新的、均匀的紫色油漆(仍然是高斯分布,但参数不同)
三、高斯混合模型(GMM)
核心思想 :用多个高斯分布的加权平均来近似任意复杂的概率分布。
高斯混合模型的概率密度函数定义为:
p(x)=∑k=1KπkN(x∣μk,Σk)p(x) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x|\mu_k, \Sigma_k)p(x)=k=1∑KπkN(x∣μk,Σk)
其中:
- KKK是高斯分量的数量
- πk\pi_kπk是第 kkk个分量的混合权重,满足0≤πk≤10 \leq \pi_k \leq 10≤πk≤1且 ∑k=1Kπk=1\sum_{k=1}^{K} \pi_k = 1∑k=1Kπk=1
- N(x∣μk,Σk)\mathcal{N}(x|\mu_k, \Sigma_k)N(x∣μk,Σk) 是第 kkk个高斯分量的概率密度函数
关键特性:
- 多模态性:高斯混合模型可以描述具有多个峰值(模式)的复杂分布
- 万能逼近:理论上,足够多的高斯分量可以逼近任何连续概率分布
- 软分配:每个数据点可以同时以不同概率属于多个分量
- 需要迭代学习:模型参数通常通过EM算法等迭代方法从数据中学习
回到颜色混合的比喻,高斯混合模型不是将颜色均匀混合,而是:
- 红色糖果(高斯分布1)
- 蓝色糖果(高斯分布2)
- 将它们放入同一个袋子,每次随机抓取一颗
你得到的不再是一种均匀的颜色,而是一个概率过程:抓到红色糖果的概率是 p1p_1p1,抓到蓝色糖果的概率是 p2p_2p2。从整体上看,这个袋子中的颜色分布是双峰的。
四、具体示例
假设我们有两种投资策略:
- 策略A:收益服从 N(5%,2%2)N(5\%, 2\%^2)N(5%,2%2)
- 策略B:收益服从 N(8%,4%2)N(8\%, 4\%^2)N(8%,4%2)
情形1:加权和
如果你将资金的60%投入策略A,40%投入策略B,那么投资组合的收益分布是:
0.6×N(5%,2%2)+0.4×N(8%,4%2)=N(0.6×5%+0.4×8%,0.62×2%2+0.42×4%2) 0.6 \times N(5\%, 2\%^2) + 0.4 \times N(8\%, 4\%^2) = N(0.6\times5\%+0.4\times8\%, 0.6^2\times2\%^2+0.4^2\times4\%^2) 0.6×N(5%,2%2)+0.4×N(8%,4%2)=N(0.6×5%+0.4×8%,0.62×2%2+0.42×4%2)
结果是单一的高斯分布 N(6.2%,0.0144%2)N(6.2\%, 0.0144\%^2)N(6.2%,0.0144%2)。
情形2:混合模型
如果你在策略A和策略B之间随机切换,60%的时间使用策略A,40%的时间使用策略B,那么你的收益分布是:
p(x)=0.6×N(x∣5%,2%2)+0.4×N(x∣8%,4%2)p(x) = 0.6 \times N(x|5\%, 2\%^2) + 0.4 \times N(x|8\%, 4\%^2)p(x)=0.6×N(x∣5%,2%2)+0.4×N(x∣8%,4%2)
这是一个双峰分布,在5%和8%附近各有一个峰值。