这一章从三个基本术语开始:均值、方差和概率. 下面是这几个术语的粗略解释:
- 均值(mean): 平均数值(average)或期望值;
- 方差 σ 2 \pmb{\sigma^2} σ2(variance): 与均值 m m m 距离的平方的平均值;
- 概率(probability): 构成样本空间的 n n n 个不同事件发生的概率是一组正数: p 1 , p 2 , ⋯ , p n p_1,p_2,\cdots,p_n p1,p2,⋯,pn,它们的和等于 1 1 1.
一、 均值
均值需要区分两种情况:一方面是从一次完整的试验得到结果(样本值);另一方面是对未来的试验的预期结果(期望值,expected values). 如下面的例子:
- 样本值(Sample values): 五位随机的大一新生的年龄为 18 , 17 , 18 , 19 , 17 \pmb{18,17,18,19,17} 18,17,18,19,17
- 样本均值(Sample mean): 1 5 ( 18 + 17 + 18 + 19 + 17 ) = 17.8 \pmb{\dfrac{1}{5}}(18+17+18+19+17)=\pmb{17.8} 51(18+17+18+19+17)=17.8
- 概率(Probabilities): 大一新生年龄及概率是 17 ( 20 % ) , 18 ( 50 % ) , 19 ( 30 % ) 17(\pmb{20\%}),18(\pmb{50\%}),19(\pmb{30\%}) 17(20%),18(50%),19(30%)
随机一个大一新生的期望年龄 (expected age) 是 E [ X ] = 0.2 × 17 + 0.5 × 18 + 0.3 × 19 = 18.1 \pmb{\textrm E[X]}=0.2×17+0.5×18+0.3×19=\pmb{18.1} E[X]=0.2×17+0.5×18+0.3×19=18.1
17.8 17.8 17.8 和 18.1 18.1 18.1 这两个数都是正确的平均值。样本均值是源自于一次完整试验的 N N N 个样本 x 1 , x 2 , ⋯ , x N x_1,x_2,\cdots,x_N x1,x2,⋯,xN,它们的均值就是这 N N N 个观测样本(obeserved samples)的平均数值: 样本均值 m = μ = 1 N ( x 1 + x 2 + ⋯ + x N ) ( 12.1.1 ) \pmb{样本均值\kern 13ptm=μ=\dfrac{1}{N}(x_1+x_2+\cdots+x_N)}\kern 25pt(12.1.1) 样本均值m=μ=N1(x1+x2+⋯+xN)(12.1.1)年龄 X X X 的数学期望 是源自于这一组年龄 x 1 , x 2 , ⋯ , x N x_1,x_2,\cdots,x_N x1,x2,⋯,xN 的概率分别为 p 1 , p 2 , ⋯ , p n p_1,p_2,\cdots,p_n p1,p2,⋯,pn:
数学期望 m = E [ X ] = p 1 x 1 + p 2 x 2 + ⋯ + p n x n ( 12.1.2 ) \pmb{数学期望\kern 14ptm=\textrm E[X]=p_1x_1+p_2x_2+\cdots+p_nx_n}\kern 18pt(12.1.2) 数学期望m=E[X]=p1x1+p2x2+⋯+pnxn(12.1.2)
这个式子就是 p ⋅ x \boldsymbol p\cdot\boldsymbol x p⋅x . 注意, m = E [ X ] m=\textrm E[X] m=E[X] 告诉我们要期待什么,而 m = μ m=μ m=μ 则告诉我们得到了什么。
通过大量的采样(样本容量 N N N 充分大),抽样的结果会趋于概率计算的结果。"大数定律(Law of Large Number)" 表明,当前样本容量 N N N 增加时,样本均值将会收敛于期望值 E [ X ] \textrm E[X] E[X]. 如抛一枚均匀的硬币,出现反面的概率 p 0 = 1 2 p_0=\dfrac{1}{2} p0=21,出现正面的概率 p 1 = 1 2 p_1=\dfrac{1}{2} p1=21,则数学期望 E [ X ] = 1 2 × 0 + 1 2 × 1 = 1 2 \textrm E[X]=\dfrac{1}{2}×0+\dfrac{1}{2}×1=\dfrac{1}{2} E[X]=21×0+21×1=21. 在 N N N 次抛硬币试验,其出现正面的比例是样本均值,接近期望 E [ X ] = 1 2 \textrm E[X]=\dfrac{1}{2} E[X]=21.
这并不意味着当出现反面的次数更多时,下一次更可能出现正面。正面和反面出现的概率都为 1 2 \dfrac{1}{2} 21. 前 100 100 100 次或 1000 1000 1000 次抛掷的结果确实会影响样本均值,但是 1000 1000 1000 次的抛掷结果不会影响它的极限 ------ 因为除数 N → ∞ N\rightarrow\infty N→∞.
二、方差(围绕均值)
方差(variance) σ 2 \pmb{\sigma^2} σ2 是衡量随机变量 X X X 与数学期望 E [ X ] \textrm E[X] E[X] 的期望距离(的平方)。样本方差(sample variance) S 2 \pmb{S^2} S2 是衡量随机变量的样本与样本均值的实际距离(的平方)。它们的平方根是标准差(standard deviation) σ \pmb\sigma σ 或 S \pmb S S .
方差始终是用于描述与样本均值或数学期望的偏差,它考虑的是样本或随机变量绕均值 x = m x=m x=m "分布(spread)" 的范围。如果样本容量为 N N N,则
样本方差 S 2 = 1 N − 1 [ ( x 1 − m ) 2 + ( x 2 − m ) 2 + ⋯ + ( x N − m ) 2 ] ( 12.1.3 ) \pmb{样本方差\kern 12ptS^2=\dfrac{1}{N-1}\Big[(x_1-m)^2+(x_2-m)^2+\cdots+(x_N-m)^2\Big]}\kern 15pt(12.1.3) 样本方差S2=N−11[(x1−m)2+(x2−m)2+⋯+(xN−m)2](12.1.3)
前面所述的例子中,年龄样本 X = 18 , 17 , 18 , 19 , 17 X=18,17,18,19,17 X=18,17,18,19,17 的均值为 17.8 17.8 17.8,则样本方差为 0.7 0.7 0.7: S 2 = 1 4 [ 0.2 2 + ( − 0.8 ) 2 + 0.2 2 + ( 1.2 ) 2 + ( − 0.8 ) 2 ] = 1 4 × 2.8 = 0.7 S^2=\dfrac{1}{4}\Big[0.2^2+(-0.8)^2+0.2^2+(1.2)^2+(-0.8)^2\Big]=\dfrac{1}{4}\times2.8=\pmb{0.7} S2=41[0.22+(−0.8)2+0.22+(1.2)2+(−0.8)2]=41×2.8=0.7由于计算的是平方,所以负号会消失。请注意!统计学家使用的除数是 N − 1 = 4 N-1=4 N−1=4(不是 N = 5 N=5 N=5),这样来保证 S 2 S^2 S2 是 σ 2 \sigma^2 σ2 的无偏估计。样本均值中已经考虑了一个自由度。
将每一个 ( x i − m ) 2 (x_i-m)^2 (xi−m)2 都展开为 x i 2 − 2 m x i + m 2 x_i^2-2mx_i+m^2 xi2−2mxi+m2,可以得到一个重要的恒等式: ∑ i = 1 N ( x i − m ) 2 = ∑ i = 1 N x i 2 − 2 m ∑ i = 1 N x i + ∑ i = 1 N m 2 = ∑ i = 1 N x i 2 − 2 m ( N m ) + N m 2 = ∑ i = 1 N x i − N m 2 ( 12.1.4 ) \pmb{\sum_{i=1}^{N}(x_i-m)^2}=\sum_{i=1}^Nx_i^2-2m\sum_{i=1}^Nx_i+\sum_{i=1}^Nm^2\\\kern 50pt=\sum_{i=1}^Nx_i^2-2m(Nm)+Nm^2\\\kern 50pt=\pmb{\sum_{i=1}^Nx_i-Nm^2}\kern 20pt(12.1.4) i=1∑N(xi−m)2=i=1∑Nxi2−2mi=1∑Nxi+i=1∑Nm2=i=1∑Nxi2−2m(Nm)+Nm2=i=1∑Nxi−Nm2(12.1.4)这是通过 x 1 2 + x 2 2 + ⋯ + x N 2 x_1^2+x_2^2+\cdots+x_N^2 x12+x22+⋯+xN2 来计算 ( x 1 − m ) 2 + ( x 2 − m ) 2 + ⋯ + ( x N − m ) 2 (x_1-m)^2+(x_2-m)^2+\cdots+(x_N-m)^2 (x1−m)2+(x2−m)2+⋯+(xN−m)2 的一个等效方法。
现在使用概率 p i p_i pi(始终非负!)来代替样本频率,我们求数学期望而不是样本值了。方差 σ 2 \sigma^2 σ2 在统计学中是一个很重要的数字:
方差 σ 2 = E [ ( X − m ) 2 ] = p 1 ( x 1 − m ) 2 + p 2 ( x 2 − m ) 2 + ⋯ + p n ( x n − m ) 2 ( 12.1.5 ) \pmb{方差\kern 16pt\sigma^2=\textrm E[(X-m)^2]=p_1(x_1-m)^2+p_2(x_2-m)^2+\cdots+p_n(x_n-m)^2\kern 16pt(12.1.5)} 方差σ2=E[(X−m)2]=p1(x1−m)2+p2(x2−m)2+⋯+pn(xn−m)2(12.1.5)
我们计算了随机变量 X X X 与数学期望 m = E [ X ] m=\textrm E[X] m=E[X] 距离的平方,没有使用抽样后的样本值,只使用了期望。我们知道概率但是并不知道实验结果。
【例1 】求上述大一新生年龄的方程 σ 2 \sigma^2 σ2.
解: 年龄为 x i = 17 , 18 , 19 x_i=17,18,19 xi=17,18,19 的概率分别为 p i = 0.2 , 0.5 , 0.3 p_i=0.2,0.5,0.3 pi=0.2,0.5,0.3.,求出期望值是 m = ∑ i = 1 3 p i x i = 18.1 \pmb{m=\sum_{i=1}^3p_ix_i=18.1} m=∑i=13pixi=18.1,则再通过概率来计算方差: σ 2 = 0.2 × ( 17 − 18.1 ) 2 + 0.5 × ( 18 − 18.1 ) 2 + 0.3 × ( 19 − 18.1 ) 2 = 0.2 × 1.21 + 0.5 × 0.01 + 0.3 × 0.81 = 0.49 \begin{array}{rl}\pmb{\sigma^2}&=0.2\times(\pmb{17-18.1})^2+0.5\times(\pmb{18-18.1})^2+0.3\times(\pmb{19-18.1})^2\\&=0.2\times\pmb{1.21}+0.5\times\pmb{0.01}+0.3\times\pmb{0.81}\\&=\pmb{0.49}\end{array} σ2=0.2×(17−18.1)2+0.5×(18−18.1)2+0.3×(19−18.1)2=0.2×1.21+0.5×0.01+0.3×0.81=0.49标准差 是方程的算术平方根,即 σ = 0.7 \pmb{\sigma=0.7} σ=0.7. 这度量了在加权概率为 0.2 , 0.5 , 0.3 0.2,0.5,0.3 0.2,0.5,0.3 的情况下,年龄为 17 , 18 , 19 17,18,19 17,18,19 围绕 E [ X ] \textrm E[X] E[X] 的分布情况。
三、连续型概率分布
迄今为止,我们所允许的有 n n n 个可能的结果 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn,如上述中的年龄 17 , 18 , 19 17,18,19 17,18,19,此时 n = 3 n=3 n=3. 如果我们用天数而不是用年来衡量年龄,那么将会有一千多个可能的结果(这样太多了)。我们还是以年来度量年龄,考虑 17 17 17 到 20 20 20 之间的每一个实数 ------ 这是一个连续的概率年龄。则此时年龄 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 对应的概率 p 1 , p 2 , p 3 p_1,p_2,p_3 p1,p2,p3 将会转到整个连续的年龄范围 17 ≤ x ≤ 20 17\le x\le20 17≤x≤20 上的概率分布(probability distribution) p ( x ) \pmb{p(x)} p(x).
我们以均匀分布(uniform distribution) 和正态分布(normal distribution) 来解释概率分布。均匀分布很简单,而正态分布非常重要。
均匀分布 假设年龄均匀分布在 17.0 17.0 17.0 和 20.0 20.0 20.0 之间,即年龄为该区间中的每一个实数都是 "等可能的",此时年龄为该区间任意一个确切实数的概率都为 0 0 0,如年龄为 x = 17.1 x=17.1 x=17.1 或 x = 17 + 2 x=17+\sqrt2 x=17+2 的概率都为 0 0 0. 此时能够有效提供(假设为均匀分布)的是,一个随机大一新生的年龄 X \pmb X X 不超过 x \pmb x x 的概率 F ( x ) \pmb{F(x)} F(x):
年龄 X 不超过 x = 17 的概率是 F ( 17 ) = 0 事件 { X ≤ 17 } 不会发生 年龄 X 不超过 x = 20 的概率是 F ( 20 ) = 1 事件 { X ≤ 20 } 一定发生 年龄 X 不超过 x 的概率是 F ( x ) = 1 3 ( x − 17 ) F 从 0 取到 1 \begin{array}{ll}年龄\,X\,不超过\,x=17\,的概率是\,F(17)=\pmb0&事件\,\{X\le17\}\,不会发生\\年龄\,X\,不超过\,x=20\,的概率是\,F(20)=\pmb1&事件\,\{X\le20\}\,一定发生\\[0.1ex]年龄\,X\,不超过\,x\,的概率是\,\pmb{F(x)=\dfrac{1}{3}(x-17)}&\pmb{F\,从\,0\,取到\,1}\end{array} 年龄X不超过x=17的概率是F(17)=0年龄X不超过x=20的概率是F(20)=1年龄X不超过x的概率是F(x)=31(x−17)事件{X≤17}不会发生事件{X≤20}一定发生F从0取到1公式 F ( x ) = 1 3 ( x − 17 ) F(x)=\dfrac{1}{3}(x-17) F(x)=31(x−17) 中,当 x = 17 x=17 x=17 时, F = 0 F=0 F=0,这表明事件 { X ≤ 17 } \{X\le17\} {X≤17} 不会发生;当 x = 20 x=20 x=20 时, F = 1 F=1 F=1,表明事件 { X ≤ 20 } \{X\le20\} {X≤20} 一定发生。这个均匀模型的累积分布函数(cumulative distribution) F ( x ) \pmb{F(x)} F(x) 在 x ∈ [ 17 , 20 ] x\in[17,20] x∈[17,20] 区间是线性递增的。
Figure 12.1 是 F ( x ) F(x) F(x) 和它的导函数(概率密度函数:probability density function ) p ( x ) p(x) p(x) 的图形:

p ( x ) d x p(x)\,\textrm dx p(x)dx 可以看成一个样本落入区间 ( x , x + d x ] (x,x+\textrm dx] (x,x+dx] 的概率,这是一个"无穷小事件": p ( x ) d x p(x)\,\textrm dx p(x)dx 是 F ( x + d x ) − F ( x ) F(x+\textrm dx)-F(x) F(x+dx)−F(x). 下面是结论: F 是 p 的积分 事件 { a < X ≤ b } 发生的概率为 ∫ a b p ( x ) d x = F ( b ) − F ( a ) ( 12.1.6 ) \pmb{F\,是\,p\,的积分\kern 13pt事件\,\{a<X \le b\}\,发生的概率为\,\int_a^bp(x)\,\textrm dx=F(b)-F(a)}\kern 15pt(12.1.6) F是p的积分事件{a<X≤b}发生的概率为∫abp(x)dx=F(b)−F(a)(12.1.6) F ( b ) F(b) F(b) 是事件 { X ≤ b } \{X\le b\} {X≤b} 发生的概率,减去 F ( a ) F(a) F(a) 之后可以保持 x > a x>a x>a,即 a < X ≤ b a<X\le b a<X≤b 的概率。
四、 p ( x ) p(x) p(x) 的均值与方差
一个概率分布的均值和方差是什么?前面我们将 p i x i \pmb{p_ix_i} pixi 加起来得到了离散型分布的均值(数学期望),而对于连续型分布,我们对 x p ( x ) \pmb{xp(x)} xp(x) 积分:
均值 m = E [ X ] = ∫ x p ( x ) d x = ∫ 17 20 x ⋅ 1 3 d x = 18.5 \pmb{均值\kern 15ptm=\textrm E[X]=\int xp(x)\,\textrm dx=\int_{17}^{20}x\cdot\dfrac{1}{3}\,\textrm dx=18.5} 均值m=E[X]=∫xp(x)dx=∫1720x⋅31dx=18.5
对于这个均匀分布,均值 m m m 是 17 17 17 和 20 20 20 的中点值,随机变量 X X X 不超过中点 m = 18.5 m=18.5 m=18.5 的概率是 F ( m ) = 1 2 F(m)=\pmb{\dfrac{1}{2}} F(m)=21.
在 MATLAB 中, X = rand(1) \textrm{X = rand(1)} X = rand(1) 等可能地选择 0 0 0 到 1 1 1 之间的一个随机数字,数学期望是 m = 1 2 m=\dfrac{1}{2} m=21,随机变量 X X X 落在区间 [ 0 , x ] [0,x] [0,x] 的概率是 F ( x ) = x F(x)=x F(x)=x,不超过均值 m m m 的概率总是 F ( m ) = 1 2 F(m)=\dfrac{1}{2} F(m)=21.
方差是随机变量 X X X 与均值距离平方的平均值。离散型分布中, σ 2 \sigma^2 σ2 是所有 p i ( x i − m ) 2 p_i(x_i-m)^2 pi(xi−m)2 的和;而连续型分布,求和就变成了积分:
方差 σ 2 = E [ ( X − m ) 2 ] = ∫ p ( x ) ( x − m ) 2 d x ( 12.1.7 ) \pmb{方差\kern 15pt\sigma^2=\textrm E[(X-m)^2]=\int p(x)(x-m)^2\,\textrm dx}\kern 18pt(12.1.7) 方差σ2=E[(X−m)2]=∫p(x)(x−m)2dx(12.1.7)
如果年龄在区间 [ 17 , 20 ] [17,20] [17,20] 上是均匀分布的,则积分区间可以转到 [ 0 , 3 ] [0,3] [0,3]: σ 2 = ∫ 17 20 1 3 ( x − 18.5 ) 2 d x = ∫ 0 3 1 3 ( x − 1.5 ) 2 d x = 1 9 ( x − 1.5 ) 3 ∣ x = 0 x = 3 = 2 9 × ( 1.5 ) 3 = 3 4 \sigma^2=\int_{17}^{20}\dfrac{1}{3}(x-18.5)^2\,\textrm dx=\int_{0}^{3}\dfrac{1}{3}(x-1.5)^2\,\textrm dx=\dfrac{1}{9}(x-1.5)^3\Big|_{x=0}^{x=3}=\dfrac{2}{9}\times(1.5)^3=\dfrac{3}{4} σ2=∫172031(x−18.5)2dx=∫0331(x−1.5)2dx=91(x−1.5)3 x=0x=3=92×(1.5)3=43这是均匀分布的一个典型例子,下面是区间 [ 0 , a ] [0,a] [0,a] 上均匀分布及概率密度 p ( x ) p(x) p(x) 的完整描述。
区间 [ 0 , a ] \pmb{[0,a]} [0,a] 上的均匀分布:密度 p ( x ) = 1 a \pmb{p(x)=\dfrac{1}{a}} p(x)=a1,分布函数 F ( x ) = x a \pmb{F(x)=\dfrac{x}{a}} F(x)=ax 均值 m = a 2 是中点值 方差 σ 2 = ∫ 0 a 1 a ( x − a 2 ) 2 d x = a 2 12 ( 12.1.8 ) \pmb{均值\,m=\dfrac{a}{2}\,是中点值\kern 20pt方差\,\sigma^2=\int_0^a\dfrac{1}{a}\Big(x-\dfrac{a}{2}\Big)^2\,\textrm dx=\dfrac{a^2}{12}}\kern 19pt(12.1.8) 均值m=2a是中点值方差σ2=∫0aa1(x−2a)2dx=12a2(12.1.8)
均值是 a a a 的倍数,方差是 a 2 a^2 a2 的倍数。当 a = 3 a=3 a=3 时, σ 2 = 9 12 = 3 4 \sigma^2=\dfrac{9}{12}=\dfrac{3}{4} σ2=129=43. 对于一个 0 0 0 到 1 1 1 之间的随机数(均值为 1 2 \dfrac{1}{2} 21)的方差是 σ 2 = 1 12 \sigma^2=\dfrac{1}{12} σ2=121.
五、正态分布:钟形曲线
正态分布也称为高斯分布,它是所有概率密度函数 p ( x ) p(x) p(x) 中最重要的一种。它的超重要性来源于独立重复试验以及实验结果的平均值,这些试验有各自的分布(如抛硬币的正反面),多次重复后的平均值近似服从正态分布。
中心极限定理 Central Limit Theorem(非正式表述): "任意" 概率分布中 N N N 个样本的平均值当 N → ∞ N\rightarrow\infty N→∞ 时近似服从正态分布。
先从 "标准正态分布" 开始,它的概率密度关于 x = 0 x=0 x=0 对称,所以均值是 m = 0 m=0 m=0,适当调整概率密度系数使得标准方差 σ 2 = 1 \sigma^2=1 σ2=1,记为 N ( 0 , 1 ) N(0,1) N(0,1).
标准正态分布的概率密度 p ( x ) = 1 2 π e − x 2 / 2 ( 12.1.9 ) \pmb{\textrm{标准正态分布的概率密度}\kern 20ptp(x)=\dfrac{1}{\sqrt{2π}}e^{-x^2/2}}\kern 20pt(12.1.9) 标准正态分布的概率密度p(x)=2π 1e−x2/2(12.1.9)
p ( x ) p(x) p(x) 的图像是如 Figure 12.2 所示的钟形曲线(bell-shaped curve) ,标准正态分布的主要特征有: 总概率为 1 ∫ − ∞ + ∞ p ( x ) d x = 1 2 π ∫ − ∞ + ∞ e − x 2 / 2 d x = 1 均值 E [ X ] = 0 m = 1 2 π ∫ − ∞ + ∞ x e − x 2 / 2 d x = 0 方差 E [ X 2 ] = 1 σ 2 = 1 2 π ∫ − ∞ + ∞ ( x − 0 ) 2 e − x 2 / 2 d x = 1 \begin{array}{ll}\pmb{总概率为\,1}&\int_{-\infty}^{+\infty}p(x)\,\textrm dx=\dfrac{1}{\sqrt{2π}}\int_{-\infty}^{+\infty}e^{-x^2/2}\,\textrm dx=\pmb1\\[1.9ex]\pmb{均值\,\textrm E[X]=0}&\pmb m=\dfrac{1}{\sqrt{2π}}\int_{-\infty}^{+\infty}xe^{-x^2/2}\,\textrm dx=\pmb 0\\[1.9ex]\pmb{方差\,\textrm E[X^2]=\pmb1}&\pmb{\sigma^2}=\dfrac{1}{\sqrt{2π}}\int_{-\infty}^{+\infty}(x-0)^2e^{-x^2/2}\,\textrm dx=\pmb1\end{array} 总概率为1均值E[X]=0方差E[X2]=1∫−∞+∞p(x)dx=2π 1∫−∞+∞e−x2/2dx=1m=2π 1∫−∞+∞xe−x2/2dx=0σ2=2π 1∫−∞+∞(x−0)2e−x2/2dx=1均值的计算很简单,因为它是对一个奇函数积分,将 x x x 换为 − x -x −x 可得 m = − m m=-m m=−m,所以均值为零。
另外两个积分比较困难,因为无法得到其原函数。Figure 12.2 是正态分布 N ( 0 , σ ) N(0,\sigma) N(0,σ) 的概率密度 p ( x ) p(x) p(x) 和对 p ( x ) p(x) p(x) 积分得到的分布函数 F ( x ) F(x) F(x) 的图形。由 p ( x ) p(x) p(x) 的对称性可以看出均值 m = 0 m=0 m=0,从 F ( x ) F(x) F(x) 可以得到一个非常重要并且实用的估计式:
服从正态分布 N ( 0 , σ ) N(0,\sigma) N(0,σ) 的随机变量 X X X 落入 − σ -\sigma −σ 到 σ \sigma σ 之间的概率是 F ( σ ) − F ( − σ ) ≈ 2 3 \pmb{F(\sigma)-F(-\sigma)\approx\dfrac{2}{3}} F(σ)−F(−σ)≈32,这是因为 ∫ − σ σ p ( x ) d x = ∫ − ∞ σ p ( x ) d x − ∫ − ∞ − σ p ( x ) d x = F ( σ ) − F ( − σ ) \int_{-\sigma}^\sigma p(x)\,\textrm dx=\int_{-\infty}^\sigma p(x)\,\textrm dx-\int_{-\infty}^{-\sigma}p(x)\,\textrm dx=F(\sigma)-F(-\sigma) ∫−σσp(x)dx=∫−∞σp(x)dx−∫−∞−σp(x)dx=F(σ)−F(−σ)同样的,落入 − 2 σ -2\sigma −2σ 到 2 σ 2\sigma 2σ ("与均值小于两个标准差")的概率是 F ( 2 σ ) − F ( − 2 σ ) ≈ 0.95 F(2\sigma)-F(-2\sigma)\approx0.95 F(2σ)−F(−2σ)≈0.95. 如果一个试验结果与均值之间的距离大于 2 σ 2\sigma 2σ,则几乎可以确定这不是偶然发生的:概率为 0.05 0.05 0.05. 药物的测试会要求更严格的确定性,如限制概率为 0.001 0.001 0.001. 寻找希格斯玻色子(Higgs boson)需要使用原理纯偶然性的 5 σ 5\sigma 5σ 超严格测试。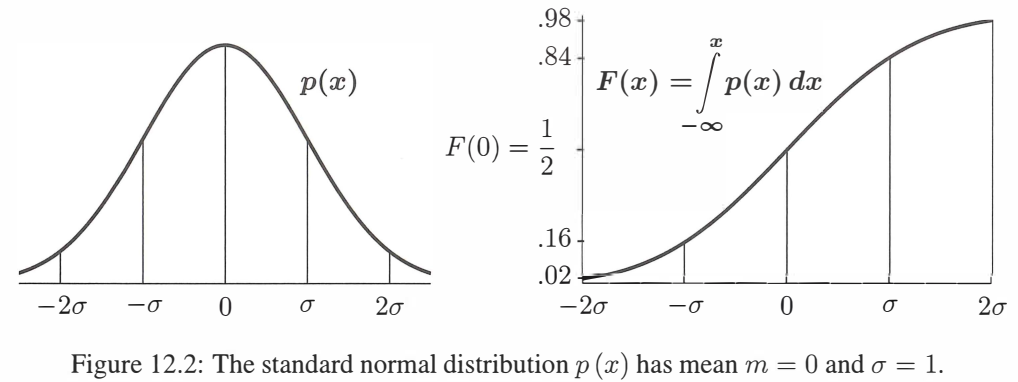
具有任意均值 m m m 和标准差 σ \sigma σ 的正态分布 N ( m , σ ) N(m,\sigma) N(m,σ) 可以通过对标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1) 的平移和伸缩变换来得到。将 x \pmb x x 平移到 x − m \pmb{x-m} x−m,将 x − m \pmb{x-m} x−m 伸缩为 ( x − m ) σ \pmb{\dfrac{(x-m)}{\sigma}} σ(x−m):
正态分布 N ( m , σ ) 的概率密度 p ( x ) p ( x ) = 1 σ 2 π e − ( x − m ) 2 / ( 2 σ 2 ) ( 12.1.10 ) \pmb{正态分布\,N(m,\sigma)\,的概率密度\,p(x)}\kern 13pt{\color{blue}p(x)=\dfrac{1}{\sigma\sqrt{2π}}e^{-(x-m)^2/(2\sigma^2)}}\kern 16pt(12.1.10) 正态分布N(m,σ)的概率密度p(x)p(x)=σ2π 1e−(x−m)2/(2σ2)(12.1.10)
p ( x ) p(x) p(x) 的积分是 F ( x ) F(x) F(x) ------ 一个随机样本不超过 x x x 的概率,微分 p ( x ) d x = F ( x + d x ) − F ( x ) p(x)\,\textrm dx=F(x+\textrm dx)-F(x) p(x)dx=F(x+dx)−F(x) 是一个随机样本落入区间 ( x , x + d x ] (x,x+\textrm dx] (x,x+dx] 的概率。计算 e − x 2 / 2 e^{-x^2/2} e−x2/2 的积分没有简单公式,因此分布函数 F ( x ) F(x) F(x) 的值被仔细计算并绘制成了表格。
六、 N N N 次抛投硬币及 N → ∞ N \rightarrow\infty N→∞
【例2 】假设随机变量 X \pmb X X 取 1 \pmb1 1 和 − 1 \pmb{-1} −1 的概率相等 p 1 = p − 1 = 1 2 \pmb{p_1=p_{-1}=\dfrac{1}{2}} p1=p−1=21,则
均值 m = 1 2 × 1 + 1 2 × ( − 1 ) = 0 \pmb m=\dfrac{1}{2}\times1+\dfrac{1}{2}\times(-1)=\pmb0 m=21×1+21×(−1)=0. 方差 σ 2 = 1 2 × 1 2 + 1 2 × ( − 1 ) 2 = 1 \pmb{\sigma^2}=\dfrac{1}{2}\times1^2+\dfrac{1}{2}\times(-1)^2=\pmb1 σ2=21×12+21×(−1)2=1.
关键的问题是平均值 A N = 1 N ( X 1 + X 2 + ⋯ + X N ) A_N=\dfrac{1}{N}(X_1+X_2+\cdots+X_N) AN=N1(X1+X2+⋯+XN),相互独立的随机变量 X i X_i Xi 的取值是 ± 1 ±1 ±1,将它们的和除以 N N N,得到 A N A_N AN 的数学期望仍为零。大数定律表明这个样本平均值趋于零的概率为 1 1 1,那么 A N A_N AN 趋于零的速度怎么样?它的方差 σ N 2 \pmb{\sigma_N^2} σN2 是什么? 由于 σ 2 = 1 \sigma^2=1 σ2=1,通过线性性质我们可得: σ N 2 = σ 2 N 2 + σ 2 N 2 + ⋯ + σ 2 N 2 = N σ 2 N 2 = 1 N ( 12.1.11 ) \pmb{\sigma_N^2}=\dfrac{\sigma^2}{N^2}+\dfrac{\sigma^2}{N^2}+\cdots+\dfrac{\sigma^2}{N^2}=N\dfrac{\sigma^2}{N^2}=\pmb{\dfrac{1}{N}}\kern 19pt(12.1.11) σN2=N2σ2+N2σ2+⋯+N2σ2=NN2σ2=N1(12.1.11)【例3 】将随机变量 X \pmb X X 的取值从 1 \pmb1 1 和 − 1 \pmb{-1} −1 变成 X = 1 \pmb{X=1} X=1 或 X = 0 \pmb{X=0} X=0,概率保持不变 p 1 = p 0 = 1 2 \pmb{p_1=p_0=\dfrac{1}{2}} p1=p0=21. 新的均值 m = 1 2 \pmb{m=\dfrac{1}{2}} m=21 落在 0 0 0 和 1 1 1 的中点,方差变为了 σ 2 = 1 4 \pmb{\sigma^2=\dfrac{1}{4}} σ2=41: m = 1 2 × 1 + 1 2 × 0 = 1 2 , σ 2 = 1 2 × ( 1 − 1 2 ) 2 + 1 2 ( 0 − 1 2 ) 2 = 1 4 \pmb m=\dfrac{1}{2}\times1+\dfrac{1}{2}\times0=\pmb{\dfrac{1}{2}},\kern 8pt\pmb{\sigma^2}=\dfrac{1}{2}\times(1-\dfrac{1}{2})^2+\dfrac{1}{2}(0-\dfrac{1}{2})^2=\pmb{\dfrac{1}{4}} m=21×1+21×0=21,σ2=21×(1−21)2+21(0−21)2=41平均值 A N A_N AN 现在的数学期望是 1 2 \dfrac{1}{2} 21,方差是 1 4 N 2 + 1 4 N 2 + ⋯ + 1 4 N 2 = 1 4 N = σ N 2 ( 12.1.12 ) \dfrac{1}{4N^2}+\dfrac{1}{4N^2}+\cdots+\dfrac{1}{4N^2}=\pmb{\dfrac{1}{4N}}=\pmb{\sigma_N^2}\kern 20pt(12.1.12) 4N21+4N21+⋯+4N21=4N1=σN2(12.1.12)此例中 σ N \sigma_N σN 是例 2 中 σ N \sigma_N σN 的一半,这个是正确的,因为新的距离 0 0 0 到 1 1 1 是 − 1 -1 −1 到 1 1 1 的一半。例 2 和例 3 展示了线性法则。
新的 0 − 1 \pmb{0-1} 0−1 变量 x new \pmb{x_{\textrm{new}}} xnew 与旧的 − 1 − 1 \pmb{-1-1} −1−1 变量之间的关系是 1 2 x old + 1 2 \pmb{\dfrac{1}{2}x_{\textrm{old}}+\dfrac{1}{2}} 21xold+21 . 所以均值 m m m 增长到 1 2 \dfrac{1}{2} 21,方差会乘 ( 1 2 ) 2 \pmb{\Big(\dfrac{1}{2}\Big)^2} (21)2. 平移会影响到 m m m,伸缩会影响到 m m m 和 σ 2 \sigma^2 σ2.
线性性质 x new = a x old + b , 则 m new = a m old + b 且 σ new 2 = a 2 σ old 2 ( 12.1.13 ) \pmb{线性性质\kern 10pt\color{blue}x_{\textrm{new}}=ax_{\textrm{old}}+b,则\,m_{\textrm{new}}=am_{\textrm{old}}+b\,且\,\sigma^2_{\textrm{new}}=a^2\sigma^2_{\textrm{old}}}\kern 18pt(12.1.13) 线性性质xnew=axold+b,则mnew=amold+b且σnew2=a2σold2(12.1.13)
下面是三个不同样本容量数值试验的结果:随机变量值为 0 或 1 , 共进行 N 次试验: N = 100 时,有 48 次 1 ; N = 10 000 时有 5035 次 1 ; N = 40 000 时,有 19967 次 1. 标准化 X = x − m σ = 2 N ( A N − 1 2 ) ,结果分别为 − 0.4 , 0.70 , − 0.33 . \boxed{\begin{array}{l}下面是三个不同样本容量数值试验的结果:随机变量值为\,0\,或\,1\,,共进行\,N\,次试验:\\N=\pmb{100}\,时,有\,\pmb{48}\,次\,1;N=\pmb{10\,000}\,时有\,\pmb{5035}\,次\,1;N=\pmb{40\,000}\,时,有\,\pmb{19967}\,次\,1.\\\pmb{标准化\,X=\dfrac{x-m}{\sigma}=2\sqrt N\Big(A_N-\dfrac{1}{2}\Big)},结果分别为\,\pmb{-0.4,0.70,-0.33}.\end{array}} 下面是三个不同样本容量数值试验的结果:随机变量值为0或1,共进行N次试验:N=100时,有48次1;N=10000时有5035次1;N=40000时,有19967次1.标准化X=σx−m=2N (AN−21),结果分别为−0.4,0.70,−0.33.中心极限定理表明,多次抛掷一枚硬币的试验结果的平均值近似服从正态分布:二项式分布近似正态分布(binomial approaches normal) . 下面看一下这是如何发生的:
每一次抛投硬币,出现正面的概率是 1 2 \dfrac{1}{2} 21,对于 N = 3 N=3 N=3 次抛投,三次都是正面的概率是 ( 1 2 ) 3 = 1 8 \Big(\dfrac{1}{2}\Big)^3=\dfrac{1}{8} (21)3=81;两次正面一次反面的概率是 3 8 \dfrac{3}{8} 83,这来自于三种情形 HHT, HTH \textrm{HHT,\,HTH} HHT,HTH 和 THH \textrm{THH} THH(其中 H H H 表示正面 head, T T T 表示反面 tail). 数字 1 8 \dfrac{1}{8} 81 和 3 8 \dfrac{3}{8} 83 都是 ( 1 2 + 1 2 ) 3 = 1 8 + 3 8 + 3 8 + 1 8 = 1 \Big(\dfrac{1}{2}+\dfrac{1}{2}\Big)^3=\pmb{\dfrac{1}{8}+\dfrac{3}{8}+\dfrac{3}{8}+\dfrac{1}{8}}=1 (21+21)3=81+83+83+81=1, 3 3 3 次抛掷出现正面的平均数是 1.5 1.5 1.5. 均值 m = 3 × 1 8 + 2 × 3 8 + 1 × 3 8 + 0 × 1 8 = 3 8 + 6 8 + 3 8 = 1.5 ( 正面 ) \pmb{均值}\kern 18ptm=3\times\dfrac{1}{8}+2\times\dfrac{3}{8}+1\times\dfrac{3}{8}+0\times\dfrac{1}{8}=\dfrac{3}{8}+\dfrac{6}{8}+\dfrac{3}{8}=\pmb{1.5\,(正面)} 均值m=3×81+2×83+1×83+0×81=83+86+83=1.5(正面)上式是 3 , 2 , 1 , 0 3,2,1,0 3,2,1,0 分别表示出现几次正面,对于 N N N 次抛投,由例 3(或常识)可以得到正面出现次数的均值 m = ∑ i = 1 n x i p i = 1 2 N \pmb{m=\sum_{i=1}^nx_ip_i=\dfrac{1}{2}N} m=∑i=1nxipi=21N.
方差 σ 2 \sigma^2 σ2 是基于到均值 N 2 \dfrac{N}{2} 2N 距离的平方得到的,对于 N = 3 N=3 N=3 次抛投,方差 σ 2 = 3 4 \sigma^2=\pmb{\dfrac{3}{4}} σ2=43,就是 N 4 \dfrac{N}{4} 4N,要求 σ 2 \sigma^2 σ2 我们需要将所有的 ( x i − m ) 2 p i (x_i-m)^2p_i (xi−m)2pi 加起来,其中均值 m = 1.5 m=1.5 m=1.5: σ 2 = ( 3 − 1.5 ) 2 × 1 8 + ( 2 − 1.5 ) 2 × 3 8 + ( 1 − 1.5 ) 2 × 3 8 + ( 0 − 1.5 ) 2 × 1 8 = 9 + 3 + 3 + 9 32 = 3 4 \pmb{\sigma^2}=(3-1.5)^2\times\dfrac{1}{8}+(2-1.5)^2\times\dfrac{3}{8}+(1-1.5)^2\times\dfrac{3}{8}+(0-1.5)^2\times\dfrac{1}{8}=\dfrac{9+3+3+9}{32}=\pmb{\dfrac{3}{4}} σ2=(3−1.5)2×81+(2−1.5)2×83+(1−1.5)2×83+(0−1.5)2×81=329+3+3+9=43对于任意的 N N N,方差 σ N 2 = N 4 \pmb{\sigma_N^2=\dfrac{N}{4}} σN2=4N,则 σ N = N 2 \sigma_N=\dfrac{\sqrt N}{2} σN=2N .
Figure 12.3 展示了 N = 4 N=4 N=4 次抛掷时正面出现 0 , 1 , 2 , 3 , 4 0,1,2,3,4 0,1,2,3,4 次的概率如何近似于一个钟形(高斯)曲线的,这个高斯分别以均值 N = N 2 N=\dfrac{N}{2} N=2N 为中心。要得到一个标准高斯分布(均值为 0 0 0,方差为 1 1 1),我们需要对图形进行平移和伸缩。如果 x x x 是 N N N 次抛投中出现正面的次数,则 N N N 个 0 − 1 0-1 0−1 分布结果的平均值,将 x x x 按均值 m = N 2 m=\dfrac{N}{2} m=2N 平移且按 σ = N 2 \sigma=\dfrac{\sqrt N}{2} σ=2N 进行伸缩来得到标准化的 X X X:
平移和伸缩 X = x − m σ = x − N / 2 N / 2 ( N = 4 时 , X = x − 2 ) 减去 m 是 "中心化" 或 "消除偏离", X 的均值为 0. 除以 σ 是 "正态化" 或 "标准化", X 的方差为 1. \begin{array}{l}\pmb{平移和伸缩}\kern 12pt{\color{blue}X=\dfrac{x-m}{\sigma}=\dfrac{x-N/2}{\sqrt N /2}}\kern 12pt(N=4\,时,\,X=x-2)\\[2.1ex]\pmb{减去\,m\,是\,"中心化"\,或\,"消除偏离",X\,的均值为\,0.}\\[1ex]\pmb{除以\,\sigma\,是 \,"正态化"\,或\,"标准化",X\,的方差为\,1.}\end{array} 平移和伸缩X=σx−m=N /2x−N/2(N=4时,X=x−2)减去m是"中心化"或"消除偏离",X的均值为0.除以σ是"正态化"或"标准化",X的方差为1.
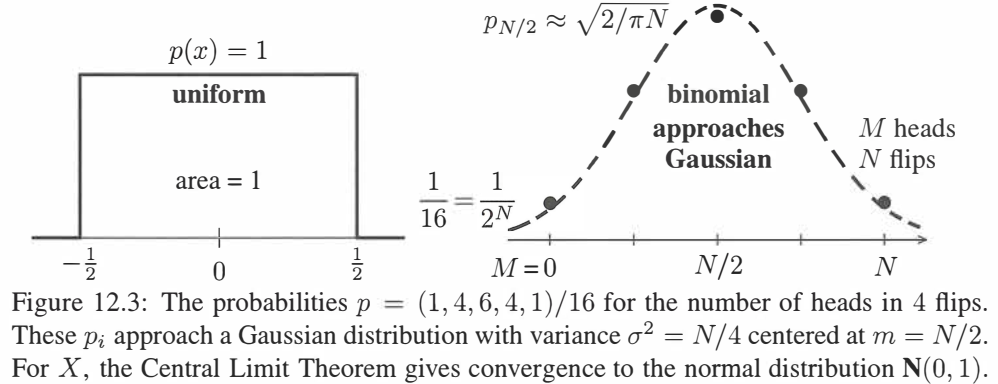
有趣的是,中心极限定理在中心点 X = 0 X=0 X=0 处给出了正确的答案,在这一点处,因子 e − X 2 / 2 = 1 e^{-X^2/2}=1 e−X2/2=1,而对于 N N N 次硬币的抛投,方差 σ 2 = N 4 \sigma^2=\dfrac{N}{4} σ2=4N,钟形曲线的中心高度是 1 2 π σ 2 = 2 N π \dfrac{1}{\sqrt{2π\sigma^2}}=\pmb{\sqrt{\dfrac{2}{Nπ}}} 2πσ2 1=Nπ2 .
二项分布 p 0 p_0 p0 到 p N p_N pN 的中心概率是什么?当 N = 4 N=4 N=4 时,正面次数是 0 , 1 , 2 , 3 , 4 0,1,2,3,4 0,1,2,3,4 次的概率来自于 ( 1 2 + 1 2 ) 4 \Big(\dfrac{1}{2}+\dfrac{1}{2}\Big)^4 (21+21)4: 中心概率 6 16 ( 1 2 + 1 2 ) 4 = 1 16 + 4 16 + 6 16 + 4 16 + 1 16 = 1 \pmb{中心概率\,\dfrac{6}{16}}\kern 16pt\Big(\dfrac{1}{2}+\dfrac{1}{2}\Big)^4=\dfrac{1}{16}+\dfrac{4}{16}+\pmb{\dfrac{6}{16}}+\dfrac{4}{16}+\dfrac{1}{16}=1 中心概率166(21+21)4=161+164+166+164+161=1由二项式定理得出任意偶数次 N N N 的中心概率 p N / 2 p_{N/2} pN/2 为:
中心概率 ( N 2 次正面, N 2 反面 ) 是 1 2 N N ! ( N / 2 ) ! ( N / 2 ) ! 中心概率\,\Big(\dfrac{N}{2}\,次正面,\dfrac{N}{2}\,反面\Big)\,是\,\kern 20pt\color{blue}\dfrac{1}{2^N}\dfrac{N!}{(N/2)!(N/2)!} 中心概率(2N次正面,2N反面)是2N1(N/2)!(N/2)!N!
对于 N = 4 N=4 N=4,由这些阶乘得 4 ! 2 ! 2 ! = 24 4 = 6 \dfrac{4!}{2!2!}=\dfrac{24}{4}=6 2!2!4!=424=6,对于比较大的 N N N,斯林特公式(Stirling's formula) 2 π N ( N e ) N \sqrt{2πN}\Big(\dfrac{N}{e}\Big)^N 2πN (eN)N 近似等于 N ! N! N!,对于分子 N N N 使用斯林特公式,对于分母 N / 2 N/2 N/2 使用两次斯林特公式: 抛投硬币试验 中心概率的极限 p N / 2 ≈ 1 2 N 2 π N ( N e ) N π N ( N 2 e ) N = 2 π N = 1 σ 2 π ( 12.1.14 ) \pmb{\begin{array}{}抛投硬币试验\\中心概率的极限\end{array}}\kern 18ptp_{N/2}\approx\dfrac{1}{2^N}\dfrac{\sqrt{2πN}\Big(\dfrac{N}{e}\Big)^N}{πN\Big(\dfrac{N}{2e}\Big)^N}=\dfrac{\sqrt2}{\sqrt{πN}}=\dfrac{1}{\sigma\sqrt{2π}}\kern 18pt(12.1.14) 抛投硬币试验中心概率的极限pN/2≈2N1πN(2eN)N2πN (eN)N=πN 2 =σ2π 1(12.1.14)最后一步我们使用了方差 σ 2 = N 4 \sigma^2=\dfrac{N}{4} σ2=4N 代入了进去,结果 1 2 π σ \dfrac{1}{\sqrt{2π\sigma}} 2πσ 1 与高斯分布概率密度的中心值相匹配。因此中心极限定理是正确的:当 N → ∞ N\rightarrow\infty N→∞ 时,"二项分布" 趋于正态分布。
七、蒙特卡罗方法
科学计算不得不处理数据中的误差,金融计算需要除了不确定的数字和预测。所有的应用数学都已经发展为接受输入的不确定性,并估计输出的方差 。
那么如何估计方差呢?通常情况下概率密度 p ( x ) p(x) p(x) 是未知的,我们能够做的就是尝试不同的输入 b \boldsymbol b b 并计算输出 x \boldsymbol x x 并且求其平均值。这是蒙特卡罗方法(Monte Carlo method) 最简单的一种形式。蒙特卡罗方法通过抽样平均 1 N ( x 1 + x 2 + ⋯ + x N ) \dfrac{1}{N}(x_1+x_2+\cdots+x_N) N1(x1+x2+⋯+xN) 来近似估计数学期望 E [ X ] . \textrm E[X]. E[X].
我们需要知道的是试验并不仅仅是抛掷硬币,因此对每个 x k x_k xk 的计算成本都比较高。每个样本值都来自于一个数据集 { b k } \{b_k\} {bk},蒙特卡罗方法是随机选择数据 b k b_k bk,计算输出 x k x_k xk,然后去这些 x k x_k xk 的平均值。要保证 E [ X ] \textrm E[X] E[X] 有较好的准确性通常需要大量的样本 b b b 和非常大的计算开销,使用 1 N ( x 1 + x 2 + ⋯ + x N ) \dfrac{1}{N}(x_1+x_2+\cdots+x_N) N1(x1+x2+⋯+xN) 来近似 E [ X ] \textrm E[X] E[X] 的误差通常在 1 N \dfrac{1}{\sqrt N} N 1 量级,准确度随着 N N N 的增大缓慢增加。
1 N \dfrac{1}{\sqrt{N}} N 1 估计出现在了抛掷硬币试验的式(12.1.11)中,对 N N N 个独立样本 x k x_k xk 取平均可以将方差 σ 2 \sigma^2 σ2 减小至 σ 2 N \dfrac{\sigma^2}{N} Nσ2.
"拟-蒙特卡罗(Quasi-Monte Carlo:QMC)" 有时可以将方差降低至 σ 2 N 2 \dfrac{\sigma^2}{N^2} N2σ2,它是非常仔细的选择输入数据 b k b_k bk ------ 并不是随机的,它们有很大的区别! 2013 2013 2013 年发表在 A c t a N u m e r i c a Acta \,Numerica ActaNumerica 上的一篇论文论述了这种 QMC \textrm{QMC} QMC 方法, 2015 2015 2015 年 Michael Giles \textrm{Michael\,Giles} MichaelGiles 在 A c t a N u m e r i c a Acta\,Numerica ActaNumerica 上概述了更新的 "多级蒙特卡罗(Multilevel Monte Carlo)" 方法,下面介绍其基本原理。
假设存在一个更简单的仿真变量 Y ( b ) Y(b) Y(b) 近似于 X ( b ) X(b) X(b),则用 N N N 个 y ( b k ) y(b_k) y(bk) 和 N ∗ < N N^*<N N∗<N 个 x ( b k ) x(b_k) x(bk) 来估算 E [ X ] \textrm E[X] E[X]:
二级蒙特卡罗方法 2-level Monte Carlo E [ X ] ≈ 1 N ∑ k = 1 N y ( b k ) + 1 N ∗ ∑ k = 1 N ∗ [ x ( b k ) − y ( b k ) ] \textrm{\pmb{二级蒙特卡罗方法\,2-level\, Monte \,Carlo}}\kern 10pt\color{blue}\textrm E[X]\approx\dfrac{1}{N}\sum_{k=1}^Ny(b_k)+\dfrac{1}{N^*}\sum_{k=1}^{N^*}[x(b_k)-y(b_k)] 二级蒙特卡罗方法2-level Monte CarloE[X]≈N1k=1∑Ny(bk)+N∗1k=1∑N∗[x(bk)−y(bk)]
相比于原始的 X X X,这个思想中 X − Y X-Y X−Y 有更小的方差 σ ∗ \sigma^* σ∗,因此在保证 E [ X ] \textrm E[X] E[X] 相同精度的情况下, N ∗ N^* N∗ 可以比 N N N 更小。我们通过 N N N 次简单的仿真得到了 y ( b k ) y(b_k) y(bk),每次计算的开销为 C C C,而只需要做 N ∗ N^* N∗ 次复杂的仿真以得到 x ( b k ) x(b_k) x(bk),每次的开销为 C ∗ C^* C∗,则总体的计算开销是 N C + N ∗ C ∗ NC+N^*C^* NC+N∗C∗.
使用微积分可以将整体方差最小化,最优比率 N ∗ N \dfrac{N^*}{N} NN∗ 是 σ ∗ σ C C ∗ \dfrac{\sigma^*}{\sigma}\sqrt{\dfrac{C}{C^*}} σσ∗C∗C . 三级蒙特卡罗方法会仿真 X , Y X,Y X,Y 和 Z Z Z: E [ X ] ≈ 1 N ∑ k = 1 N z ( b k ) + 1 N ∗ ∑ k = 1 N ∗ [ y ( b k ) − z ( b k ) ] + 1 N ∗ ∗ ∑ k = 1 N ∗ ∗ [ x ( b k ) − y ( b k ) ] \pmb{\textrm E[X]\approx\dfrac{1}{N}\sum_{k=1}^Nz(b_k)+\dfrac{1}{N^*}\sum_{k=1}^{N^*}[y(b_k)-z(b_k)]+\dfrac{1}{N^{**}}\sum_{k=1}^{N^{**}}[x(b_k)-y(b_k)]} E[X]≈N1k=1∑Nz(bk)+N∗1k=1∑N∗[y(bk)−z(bk)]+N∗∗1k=1∑N∗∗[x(bk)−y(bk)]Giles 通过优化 N , N ∗ , N ∗ ∗ , ⋯ N,N^*,N^{**},\cdots N,N∗,N∗∗,⋯ 来保证 E [ X ] ≤ E 0 \textrm E[X]\le E_0 E[X]≤E0(其中 E 0 E_0 E0 是固定值),还提供了 MATLAB 代码。
八、回顾:计算均值与方差的三个公式
计算均值 m m m 和方差 σ 2 \sigma^2 σ2 的公式是概率统计理论的基础。共有三种不同的情况:样本值 x i x_i xi,期望值 (离散型 p i p_i pi)和期望值 的区间(连续型 p ( x ) p(x) p(x)). 下面是这三种情况下均值和方差的公式:
样本值为 x 1 , x 2 , ⋯ , x N m = x 1 + x 2 + ⋯ + x N N , S 2 = ( x 1 − m ) 2 + ( x 2 − m ) 2 + ⋯ + ( x N − m ) 2 N − 1 n 个可能输出值的概率为 p i m = ∑ i = 1 n p i x i , σ 2 = ∑ i = 1 n p i ( x i − m ) 2 X 的概率密度为 p ( x ) m = ∫ x p ( x ) d x , σ 2 = ∫ ( x − m ) 2 p ( x ) d x \begin{array}{lll}\pmb{样本值为\,x_1,x_2,\cdots,x_N}&\pmb m=\dfrac{x_1+x_2+\cdots+x_N}{N},&\pmb{S^2}=\dfrac{(x_1-m)^2+(x_2-m)^2+\cdots+(x_N-m)^2}{N-1}\\\pmb{n\,个可能输出值的概率为\,p_i}&\pmb m=\sum_{i=1}^np_ix_i,&\pmb{\sigma^2}=\sum_{i=1}^np_i(x_i-m)^2\\[0.8ex]\pmb{X\,的概率密度为\,p(x)}&\pmb m=\int xp(x)\,\textrm dx,&\pmb{\sigma^2}=\int(x-m)^2p(x)\,\textrm dx\end{array} 样本值为x1,x2,⋯,xNn个可能输出值的概率为piX的概率密度为p(x)m=Nx1+x2+⋯+xN,m=∑i=1npixi,m=∫xp(x)dx,S2=N−1(x1−m)2+(x2−m)2+⋯+(xN−m)2σ2=∑i=1npi(xi−m)2σ2=∫(x−m)2p(x)dx
一个自然的问题:为什么开头的公式中没有概率 p p p 呢?这些公式在本质上是如何保持一致的?答:我们将 X = x i X=x_i X=xi 发生的频率 p i p_i pi 视为概率,那么 X = x i X=x_i X=xi 重复出现 p i N p_iN piN 次,则前两个公式会得到相同的 m m m.
当我吗处理样本时并不知道概率 p i p_i pi,只能将每一个输出结果 X = x i X=x_i X=xi 记录下来,所得到的是 "经验(empirical)" 均值而不是期望均值。