MDMLP-EIA: Multi-domain Dynamic MLPs with Energy Invariant Attention for Time Series Forecasting
Simple Moving Average(SMA)简单移动平均
简单移动平均 是一种通过计算滑动窗口内数据均值来提取时间序列趋势项的方法。
在Autoformer、Dlinear等模型中,SMA被用于将原始数据分解为趋势(Trend)和季节性(Seasonality)两部分。
SMA公式:
st=1k∑i=tt+k−1xi=xt+xt+1+...+xt+k−1k s_{t} = \frac{1}{k} \sum_{i=t}^{t+k-1} x_{i} = \frac{x_{t} + x_{t+1} + ... + x_{t+k-1}}{k} st=k1i=t∑t+k−1xi=kxt+xt+1+...+xt+k−1
参数解释:
- X={x1,x2,...,xn}X = \{x_1, x_2, ..., x_n\}X={x1,x2,...,xn}:原始的时间序列数据点。
- kkk :滑动窗口的大小(Kernel size),即每次计算平均值时包含的数据点个数(例如 k=3k=3k=3 或 k=25k=25k=25)。
- ttt:当前的移动步数(时间步索引)。
- sts_tst :计算得到的第 ttt 个移动平均值。
具体计算过程:
① 填充(Padding)
由于移动平均操作会导致序列长度变短,为了保证输出的趋势序列长度与原始序列一致,必须在序列的两端进行填充 。实现是:重复序列的第一个值填充在头部,重复最后一个值填充在尾部。
② 滑动窗口计算(Moving Average)
假设有一个长度为k的窗口,它在数据上滑动。对于每一个位置,选择窗口内k个数值的无加权平均值。
③ 分解结果
趋势项:XT=AvgPool(Padding(X))X_T = AvgPool(Padding(X))XT=AvgPool(Padding(X))
季节性项:XS=X−XTX_S=X-X_TXS=X−XT
Exponential Moving Average(EMA) 指数移动平均
指数移动平均 指的是它对数据点进行加权平均 ,但权重不是相等的 。它给最新的数据点分配更大的权重,而对较旧的数据点分配较小的权重 ,这种权重随时间呈指数级衰减。这种机制使得EMA能够更迅速地响应时间序列中潜在趋势的变化,同时平滑掉旧数据的噪音。
具体计算过程:
① 初始化
序列的第一个点的EMA值(趋势值s0s_0s0)直接等于原始数据中的第一个点x0x_0x0
② 递归计算
从第二个时间点开始(t>0t>0t>0),每一个新的EMA值sts_tst都是由当前时刻的原始数据xtx_txt和上一时刻的EMA值st−1s_{t-1}st−1加权混合而成的。
st=αxt+(1−α)st−1 s_t = \alpha x_t + (1 - \alpha)s_{t-1} st=αxt+(1−α)st−1
xtx_txt:当前时刻的原始数据输入。
st−1s_{t-1}st−1:上一时刻计算出的趋势值(包含了过去的历史信息)。
α\alphaα (Alpha) :平滑因子 ,取值范围是 0<α<10 < \alpha < 10<α<1 。
③ 分解结果
计算整个序列的EMA值之后,将原始时间序列X分解为两部分:
趋势项:XTX_TXT=EMA(x)EMA(x)EMA(x)
季节性项:XsX_sXs=X−XTX - X_TX−XT
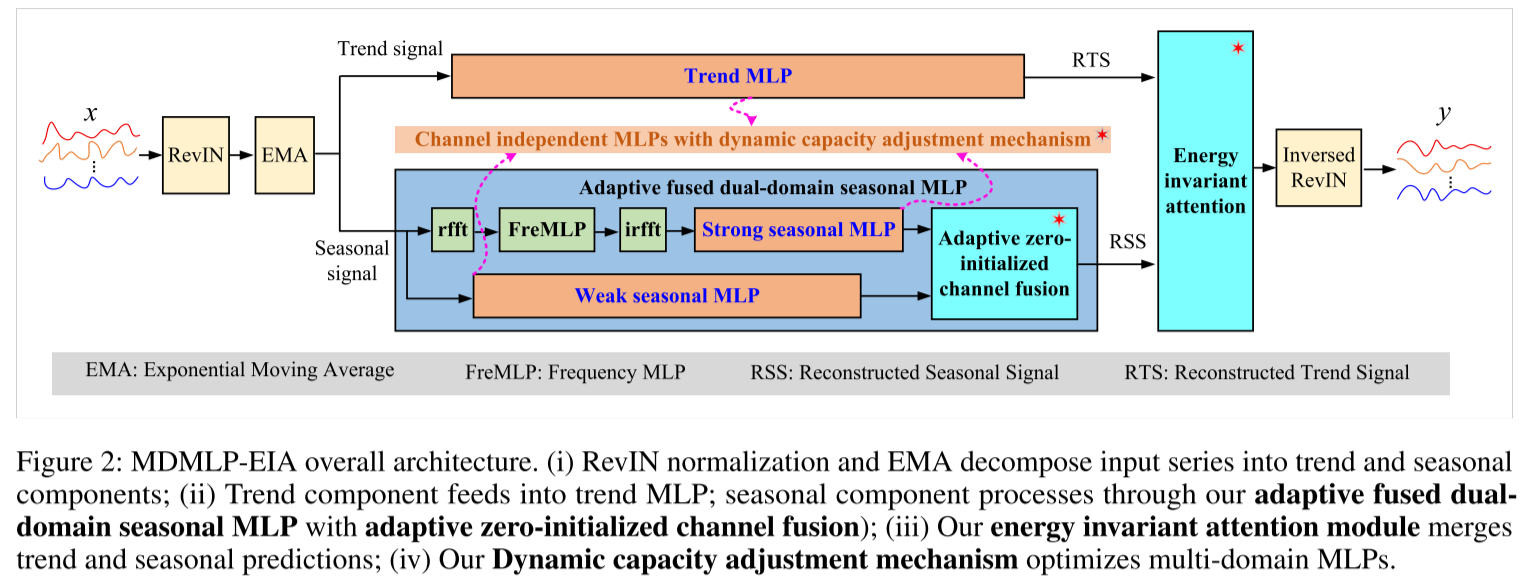
自适应融合的季节性MLP
为了在最小化噪声干扰的同时有效捕捉弱季节性信号 ,我们将季节性信号划分为强、弱分量 ,分别通过频域MLP和标准MLP进行处理。
频域 MLP 与强季节性 MLP : 采用了一种时频学习器(包含嵌入、实数 FFT、频域 MLP 和逆实数 FFT)来重构具有强季节性模式的特征 f_{s1} \\in \\mathbb{R}\^{C \\times L \\times E}10。随后,一个强季节性 MLP 从 fs1f_{s1}fs1 中学习预测值 y_{21} \\in \\mathbb{R}\^{Q \\times C}11
弱季节性MLP :时频学习器使用软阈值(softshrink)处理来降低噪声,但这不可避免地丢失了低幅度的弱季节性信号 。因此,我们构建了一个弱季节性 MLP,直接从季节性信号 中提取弱季节性预测。
AZCF(自适应零初始化通道融合)机制: 现有的时间序列信号融合方法通常使用注意力机制在通道和时间维度上对信号进行加权14。给定强季节性预测 y21y_{21}y21 和弱季节性预测 y22y_{22}y22,完整的季节性预测 y2y_2y2 通常计算为 y2=α1⊙y21+α2⊙y22y_2 = \alpha_1 \odot y_{21} + \alpha_2 \odot y_{22}y2=α1⊙y21+α2⊙y22,其中权重是通过 Query-Key-Value 变换间接获得的。然而,这种间接方法引入了不必要的复杂性,且忽略了强弱季节性预测之间显著的信噪比差异。因此,我们提出了具有三个关键特征的 AZCF 机制:
单参数融合 (Single-parameter fusion) : 我们引入一个自适应权重系数 α\alphaα 来调节弱季节性预测的贡献:
y2=y21+α⊙y22 y_2 = y_{21} + \alpha \odot y_{22} y2=y21+α⊙y22
其中 α∈RQ×C\alpha \in \mathbb{R}^{Q \times C}α∈RQ×C。这种单参数融合首先确保了强信号的质量,然后选择性地增强弱信号,同时减少模型参数。
通道维度融合 (Channel-dimension fusion): 由于 y21y_{21}y21 和 y22y_{22}y22 均通过通道独立方法获得,融合策略应尊重这一分离特性,在通道维度上进行独立决策,学习哪些特征拥有更可靠的弱季节性信号。沿时间维度融合会破坏季节性模式的时间连贯性,并可能在通道间传播噪声。因此,我们将 α\alphaα 定义为 α={α1,...,αC}∈R1×C\alpha = \{\alpha_1, ..., \alpha_C\} \in \mathbb{R}^{1 \times C}α={α1,...,αC}∈R1×C,并通过广播机制将其扩展到输出时间步维度。
零初始化 (Zero initialization): 我们将 α\alphaα 初始化为零向量,从最可靠的强季节性预测开始:\\alpha_{init} = 0 \\in \\mathbb{R}\^{1 \\times C}22。这给出了初始预测 y2init=y21y_2^{init} = y_{21}y2init=y21。
Energy Invariant Attention(EIA)能量不变注意力
EIA (Energy Invariant Attention) 是一种带物理约束的加权融合策略。
传统的基于分解的方法 通常通过直接将趋势预测 y1y_1y1 和季节性预测 y2y_2y2 相加来生成最终预测 y3y_3y3 (y3=y1+y2y_3 = y_1 + y_2y3=y1+y2) 。然而,这种方法可能限制了模型处理跨通道和时间步的、变化的、时间动态特征重要性的自适应能力。
基于归一化注意力加权 的方法让模型学习一个参数β\betaβ, yfinal=β⋅ytrend+(1−β)⋅yseasony_{final} = \beta \cdot y_{trend} + (1-\beta) \cdot y_{season}yfinal=β⋅ytrend+(1−β)⋅yseason, 预测出的信号幅度会坍塌(Shrink) ,变得比真实值小很多。为了弥补这个幅度亏损,模型可能会被迫把 β\betaβ 学习得非常极端。
EIA能量不变注意力:
yfinal=2×[β⋅ytrend+(1−β)⋅yseason] y_{final} = \mathbf{2} \times [\beta \cdot y_{trend} + (1-\beta) \cdot y_{season}] yfinal=2×[β⋅ytrend+(1−β)⋅yseason]
凸组合(加权平均)在数学上隐含了一个"除以2"的归一化效果, EIA 通过乘以 2,把幅度补偿回来。