一、原理介绍
前文已经介绍过了增量式无差拍电流预测控制,得到结论增量式DPCC可以消除对转子磁链变化的影响,但是从参数变化导致的电流误差公式可知,电感和电阻依旧会影响算法预测的准确性以及系统运行的稳定性。为了消除其余参数的影响,引入增量式ESO,通过将不可测的内外扰动拓展成新的状态变量并反馈至dq轴电压信号输出来增强抗扰性。增量式ESO公式如下:
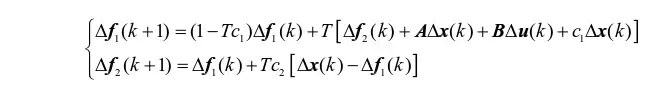
其整体控制框图如下所示
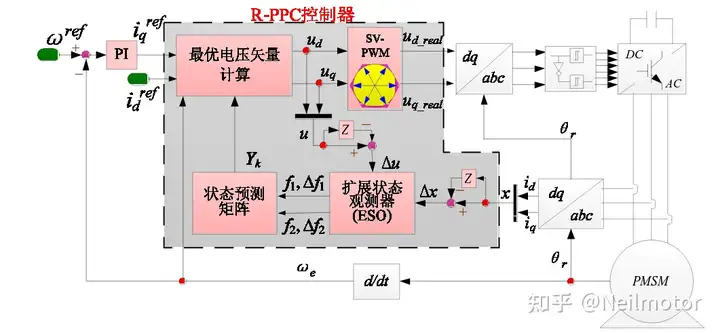
二、仿真模型(编号392)
在MATLAB/simulink里面验证所提算法,搭建仿真。采用和实验中一致的采样、控制周期1e-4,电机部分计算周期为5e-7。仿真模型如下所示:
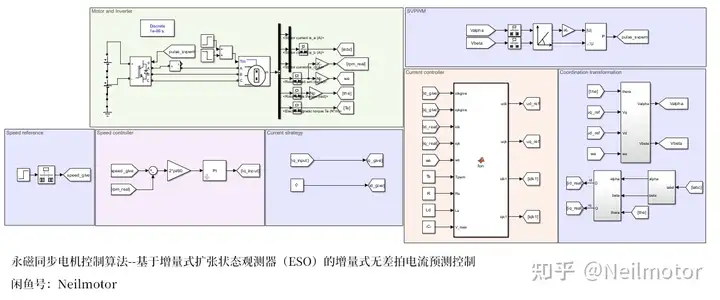
ESO以及DPCC算法通过在MATLAB function中编程实现
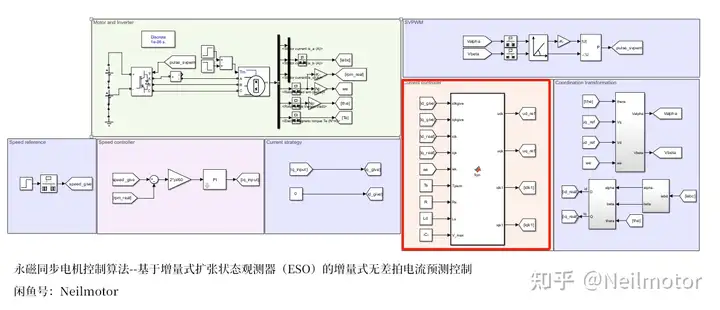
仿真工况:电机空载零速启动,给定转速为1000rpm,0.5s施加额定负载,1s撤掉负载,设置1拍数字延迟。将不带ESO的增量式无差拍电流预测控制(上)与带ESO的增量式无差拍电流预测控制(下)进行对比。
在参数准确时,ESO基本不起作用,这里就不再展示对比波形,直接从参数存在误差开始。
2.1 磁链变化
0.5倍磁链下dq轴预测电流与实际电流
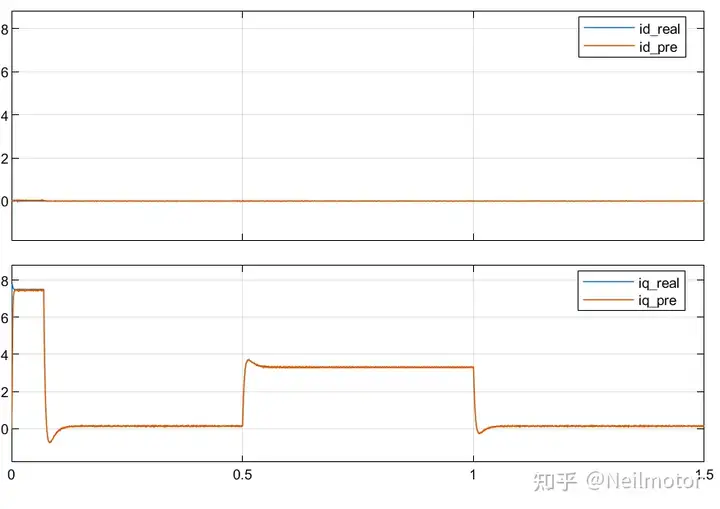

1.5倍磁链下dq轴预测电流与实际电流
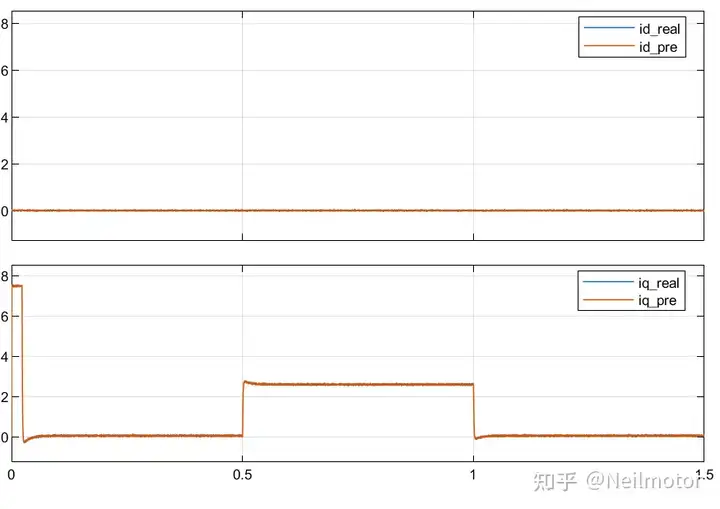
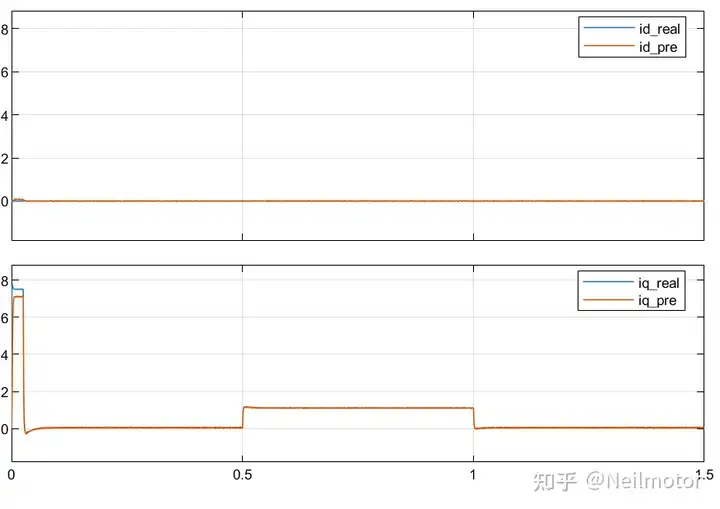
可以看出在磁链发生变化时,由于增量式DPCC在公式中消除磁链的特点,无论是否增加ESO算法都可以实现准确的控制性能。细心的读者可能发现在1.5倍磁链状态下,带ESO的增量式DPCC在启动加速阶段存在一段误差,造成这个的原因是ESO在此阶段受设置带宽影响。将ESO带宽增大至500*2*pi后波形如下,可以看出静差基本消除。
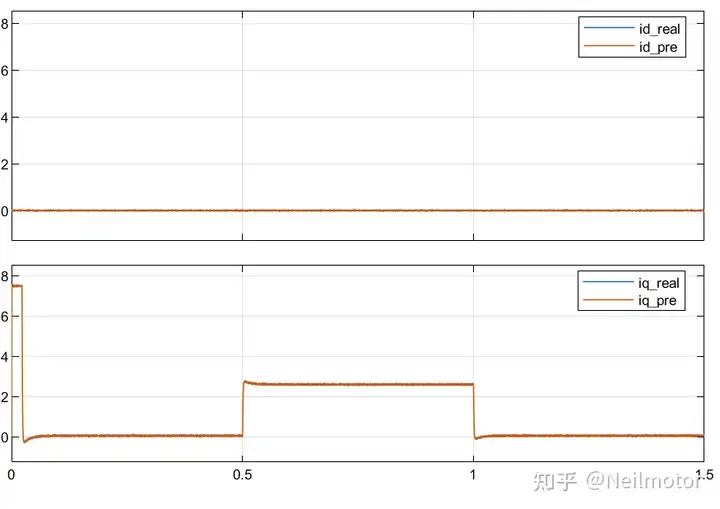
2.2 电感、电阻变化
保持电机中转子磁链为0.5倍额定值,将电感、电阻设置为1.5倍额定值
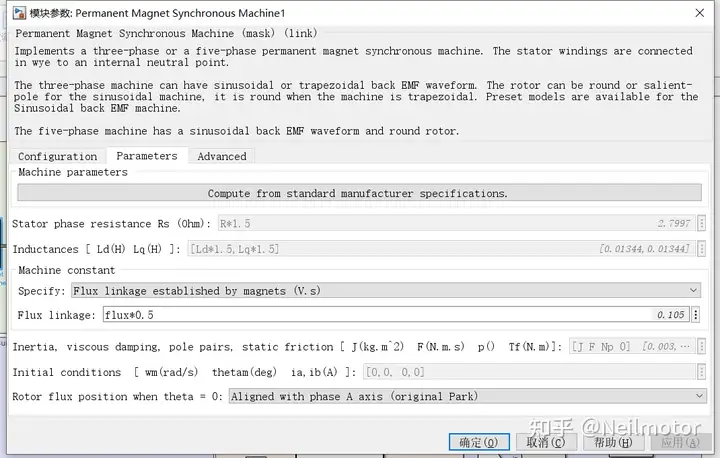
dq轴预测电流与实际电流
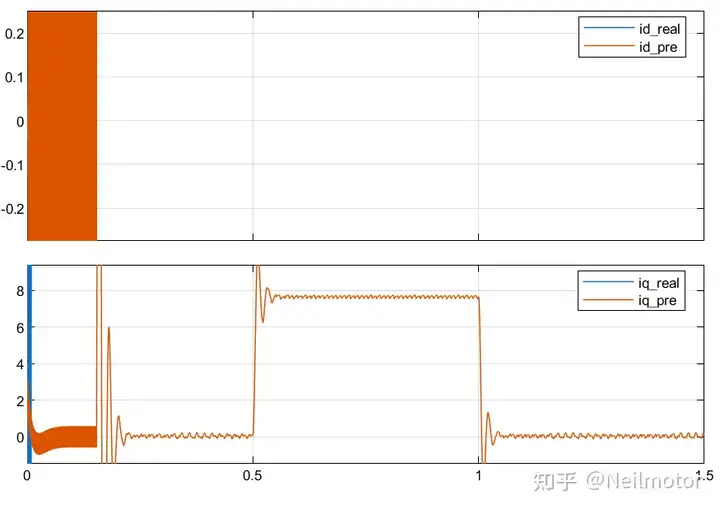
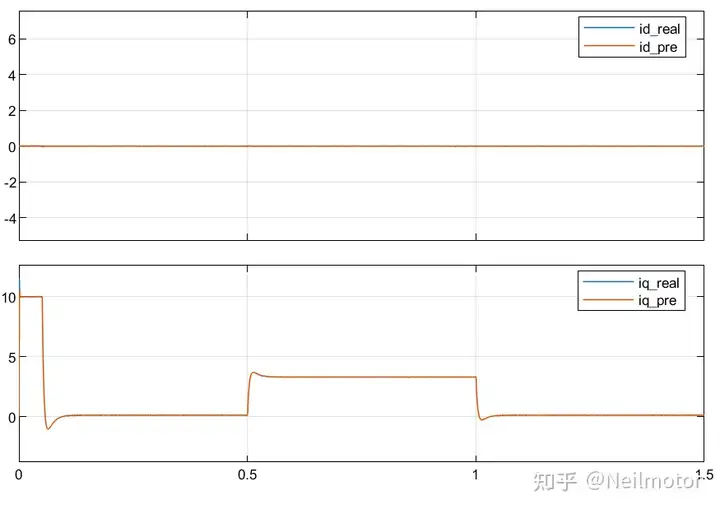
可以看出,不带ESO的增量式DPCC已经失去稳定,而带ESO的增量式DPCC跟参数准确时相比基本没有变化,预测电流和实际电流基本重合,ESO环节有效实现了对参数误差导致的干扰的估计和补偿。