【人工智能学习-AI-MIT公开课第 16 讲：支持向量机（SVM）】

人工智能学习-AI-MIT公开课第 16 讲：支持向量机（SVM）

1-前言
2-课程链接
3-具体内容解释说明
一、支持向量机（SVM）在"学习"里是干什么的？
[二、SVM 想解决的核心问题（一定会考）](#二、SVM 想解决的核心问题（一定会考）)
三、什么叫「最大间隔（マージン最大化）」？
- [1️⃣ 间隔（margin）是什么](#1️⃣ 间隔（margin）是什么)
- [2️⃣ 支持向量（Support Vector）](#2️⃣ 支持向量（Support Vector）)
[四、线性 SVM vs 非线性 SVM（超高频）](#四、线性 SVM vs 非线性 SVM（超高频）)
- [1️⃣ 线性 SVM](#1️⃣ 线性 SVM)
- [2️⃣ 非线性 SVM & 核函数（Kernel）](#2️⃣ 非线性 SVM & 核函数（Kernel）)
[五、软间隔（ソフトマージン）与参数 C](#五、软间隔（ソフトマージン）与参数 C)
- - [参数 C（超重要）](#参数 C（超重要）)
[六、SVM 在考试里的常见问法](#六、SVM 在考试里的常见问法)
- - [① 概念判断](#① 概念判断)
  - [② 对比题](#② 对比题)
  - [③ 性质题](#③ 性质题)
七、一句话「入试标准总结」（背这个）
4-课后练习（日语版本）
- 【問題1】支持向量の役割（基本）
- 【問題2】マージン最大化の意味
- [【問題3】ソフトマージンとパラメータ C（必出）](#【問題3】ソフトマージンとパラメータ C（必出）)
- 【問題4】カーネル法の本質
5-课后练习（日语版本）解析
- 【問題1】支持向量的决定因素（❌）
- - 你的选择：D
  - 正解：C
  - [❌ 错因解析（这是**高频陷阱**）](#❌ 错因解析（这是高频陷阱）)
- 【問題2】マージン最大化的目的（✅）
- - 你的选择：C（完全正确）
- [【問題3】参数 C 的作用（❌ 但这是"好错"）](#【問題3】参数 C 的作用（❌ 但这是“好错”）)
- - 你的选择：D
  - 正解：B
  - [❌ 错因解析](#❌ 错因解析)
- 【問題4】核方法的本质（✅）
- - 你的选择：B（完全正确）
总体评价（非常重要）
6-总结

1-前言

为了应对大学院考试，我们来学习相关人工智能相关知识，并且是基于相关课程。使用课程为MIT的公开课。

通过学习，也算是做笔记，让自己更理解些。

2-课程链接

是在B站看的视频，链接如下：
https://www.bilibili.com/video/BV1dM411U7qK?spm_id_from=333.788.videopod.episodes&vd_source=631b10b31b63df323bac39281ed4aff3&p=16

3-具体内容解释说明

一、支持向量机（SVM）在"学习"里是干什么的？

一句话版（考试可用）👇

支持向量机是一种通过最大化分类间隔来进行分类或回归的监督学习方法。

再白一点👇

👉 不是先想怎么分，而是先想"怎么把两类分得最稳"

二、SVM 想解决的核心问题（一定会考）

给你一堆已标注的数据点（二维最容易画图）：

圆圈是正类
叉号是负类

问题不是：

有没有一条线能分？

而是：

哪一条线"最安全"？

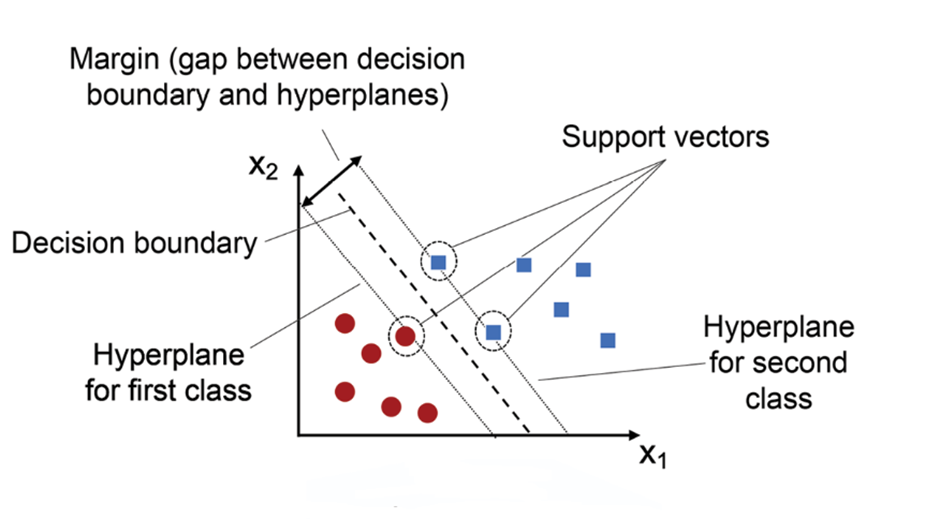
三、什么叫「最大间隔（マージン最大化）」？

1️⃣ 间隔（margin）是什么

分隔超平面（直线/平面）
到最近样本点的最小距离

👉 SVM 的目标是：

让这条"最近距离"尽可能大

2️⃣ 支持向量（Support Vector）

决定这条最优分隔线的点，叫做：

👉 支持向量

离分隔线最近的点
不是所有样本都重要
只看最"危险"的那些点

📌 这点在入试里非常爱考：

"支持向量机中，分类境界由哪类样本决定？"

正确理解：

✅ 由支持向量决定

四、线性 SVM vs 非线性 SVM（超高频）

1️⃣ 线性 SVM

数据可以用一条直线/平面分开
直接找最优超平面

2️⃣ 非线性 SVM & 核函数（Kernel）

如果数据长这样👇

⭕⭕ ❌❌ 混在一起

怎么办？

👉 不在原空间分

👉 映射到高维再分

这就是 核技巧（Kernel Trick）

常见核函数（名字要认识）：

核函数	日文	说明
線形カーネル	Linear	最基础
多項式カーネル	Polynomial	弯曲边界
ガウスカーネル	RBF	最常考

📌 入试不会让你算，只问作用和意义

五、软间隔（ソフトマージン）与参数 C

现实数据一定有噪声 👇

👉 允许少量分错

这时引入：

参数 C（超重要）

C 大
👉 少容错，追求训练正确率（容易过拟合）
C 小
👉 多容错，间隔大（泛化能力强）

📌 考试常问：

"C 的作用是什么？"

标准答法：

调节间隔大小与误分类惩罚之间的权衡

六、SVM 在考试里的常见问法

① 概念判断

SVM 的目标函数是什么？
支持向量的含义？

② 对比题

SVM vs パーセプトロン（感知机）
SVM vs 最近傍法（k-NN）

③ 性质题

为什么 SVM 泛化能力强？
为什么核函数可以处理非线性？

七、一句话「入试标准总结」（背这个）

支持向量机是一种监督学习方法，通过最大化分类间隔来提高泛化性能，分类境界由支持向量决定，并可通过核函数处理非线性问题。

4-课后练习（日语版本）

【問題1】支持向量の役割（基本）

線形分離可能な 2 クラス分類問題において，

支持向量機（SVM）によって得られる分類境界について，
最も適切な説明はどれか。

a. すべての学習データ点が分類境界の決定に等しく寄与する

b. 分類境界はクラスの重心の位置によって決定される

c. 分類境界は，境界に最も近い一部のデータ点によって決定される

d. 分類境界は誤分類率が最小となるように決定される

【問題2】マージン最大化の意味

支持向量機において，マージンを最大化する ことの主な目的として

最も適切なものはどれか。

a. 学習データに対する分類精度を必ず 100% にするため

b. 計算量を削減するため

c. 未知データに対する汎化性能を向上させるため

d. 学習時間を短縮するため

【問題3】ソフトマージンとパラメータ C（必出）

ソフトマージン SVM における パラメータ C の役割として，

最も適切なものはどれか。

a. 入力空間を高次元空間に写像する強さを調整する

b. マージンの大きさと誤分類に対するペナルティのバランスを調整する

c. 支持ベクトルの個数を直接指定する

d. 学習に用いるカーネル関数の種類を決定する

【問題4】カーネル法の本質

カーネル法を用いた支持向量機に関する説明として，
最も適切なものはどれか。

a. 入力データを明示的に高次元空間へ写像してから学習を行う

b. 非線形分類問題を線形分類問題として扱うことを可能にする

c. 学習データが線形分離可能であることを保証する

d. 支持ベクトルの数を必ず減少させる

5-课后练习（日语版本）解析

【問題1】支持向量的决定因素（❌）

你的选择：D

誤分類率が最小となるように決定される

正解：C

境界に最も近い一部のデータ点によって決定される

❌ 错因解析（这是高频陷阱）

你把 SVM 和 最小誤分類（ERM） 混在一起了。

❌ SVM 不是"最小誤分類率"
✅ SVM 是"最大マージン"

即使：

两条分界线分类结果一样
SVM 仍会选 间隔最大的那一条

📌 入试关键句（记住）：

支持向量機は誤分類率最小化ではなく，マージン最大化を目的とする

【問題2】マージン最大化的目的（✅）

你的选择：C（完全正确）

未知データに対する汎化性能を向上させる

这是 100% 标准答案，

✔ 不需要修改。

【問題3】参数 C 的作用（❌ 但这是"好错"）

你的选择：D

カーネル関数の種類を決定する

正解：B

マージンと誤分類ペナルティのバランスを調整

❌ 错因解析

你把 C 和 核函数 γ / kernel type 混了。

❌ C ≠ 核函数
❌ C ≠ 映射方式
✅ C = 容错 vs 间隔的权衡

📌 入试安全句式：

C が大きいほど誤分類を強く抑制し，小さいほどマージンを重視する

【問題4】核方法的本质（✅）

你的选择：B（完全正确）

非線形問題を線形問題として扱うことを可能にする

这是 东大风格标准表述。

✔ 非常好，说明你理解"核技巧"的思想，而不是死记。

总体评价（非常重要）

你现在的状态是 👇

✅ 理解层面：有
❌ 术语边界：还不稳
⚠️ 容易被"目的函数 vs 结果"混淆

但我要强调一句：

❗你错的不是"不会"，而是"把不同算法的思想混在了一起"。

这是 可以 1～2 天内完全修正的问题。

6-总结

知识一点点记录吧，最后应对考试，打下基础