赛事链接
B站看到的一个博主张云翼_like,讲了自己参加比赛,提供了题目下载链接,下载下来自己做一下
第一题
通过Reference列的数据来获取右侧对应列表
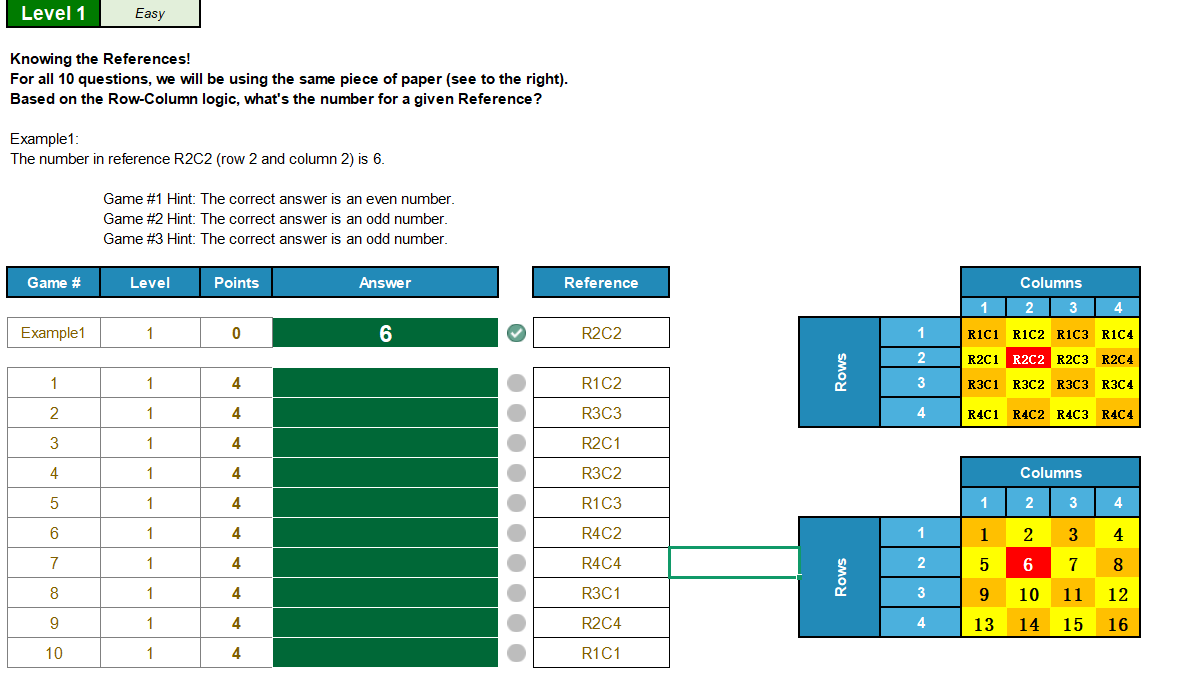
应该有其他字符串的解析方法,我是java开发,正则比较熟悉,对excel的语法不是很懂
通过REGEXP进行解析
获取到所有的数字字符串
=REGEXP(G61, "\d", 0)
通过INDEX获取到单个数字
=INDEX(REGEXP(G61, "\d", 0), 1)
=INDEX(REGEXP(G61, "\d", 0), 2)
通过INDEX获取到映射表数字
=INDEX(
$K$66:$N$69,
INDEX(REGEXP(G61, "\d", 0), 1),
INDEX(REGEXP(G61, "\d", 0), 2)
) 第二题
在Sheet (of Paper)页获取到以Center Cell列对应为中心,大小为size列的正方形的形状数字的求和

先随意找个cell,点一下获取到单元格的样式
='Sheet (of Paper)'!K7
通过INDIRECT来获取到中心单元格位置
=INDIRECT("'Sheet (of Paper)'!" & H93)
因为是中心,所以size肯定是奇数,因此用减一除以2的方式,就能获取到
通过OFFSET,获取到左上角位置
=OFFSET(
INDIRECT(
"'Sheet (of Paper)'!" & H93
),
(1 - G93) / 2,
(1 - G93) / 2
)
通过OFFSET,获取到右下角位置
OFFSET(
INDIRECT(
"'Sheet (of Paper)'!" &
H93
),
(G93 - 1) / 2,
(G93 - 1) / 2
)
然后求和一下即可获得结果
=SUM(
OFFSET(
INDIRECT(
"'Sheet (of Paper)'!" & H93
),
(1 - G93) / 2,
(1 - G93) / 2
) :
OFFSET(
INDIRECT(
"'Sheet (of Paper)'!" &
H93
),
(G93 - 1) / 2,
(G93 - 1) / 2
)
)第三题
通过Top Left Cell列对应单元格定位,往右下扩展8x8的一个区域,通过对称的形式,把右边的覆盖左边的
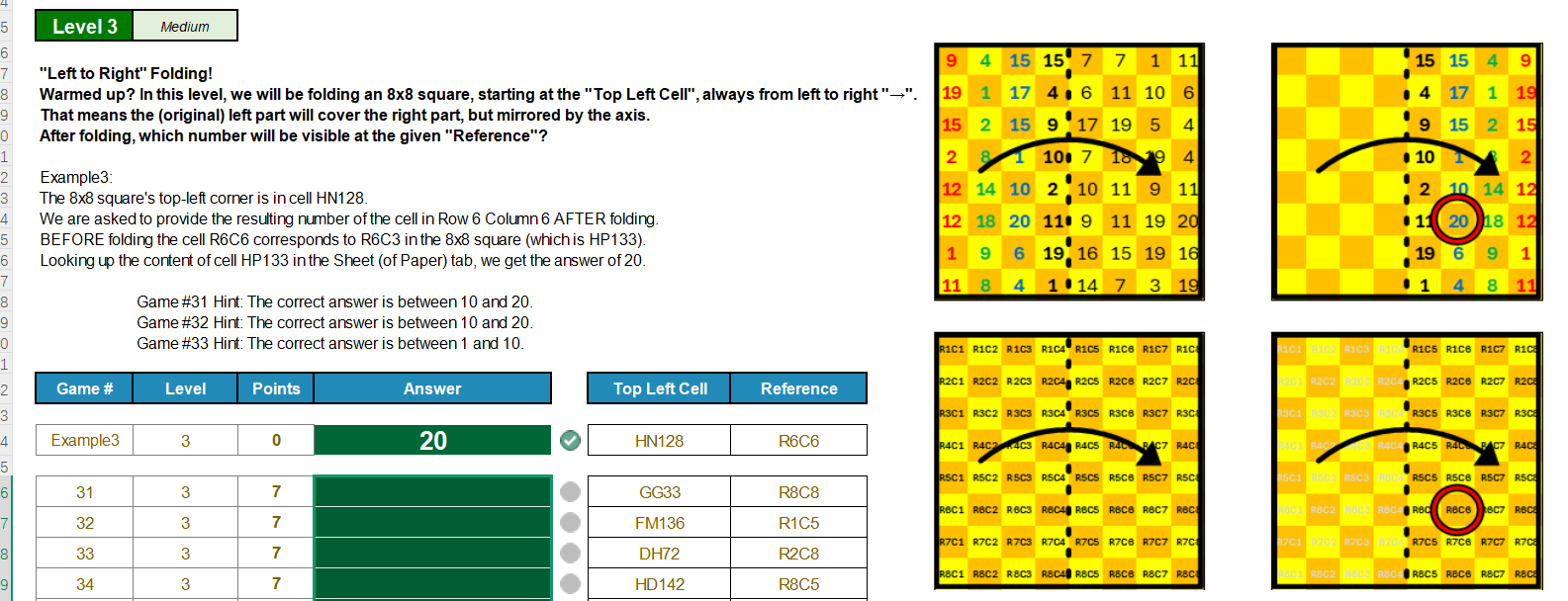
思路很明显还是INDIRECT获取到对应位置,OFFSET获取到8x8的范围,正则解析到Reference列的RC对应行列
因为对称关系,12345678其实对应12344321,这个可以通过MIN(val,9-val)进行判断
定位到左上角
=INDIRECT("'Sheet (of Paper)'!" & G136)
定位到右下角
=OFFSET(INDIRECT("'Sheet (of Paper)'!" & G136),8,8)
定位R
=INDEX(REGEXP(H136, "\d", 0), 1)
定位C,此时我观察到所有C都大于4,因此不需要通过MIN进行二次判断,直接用9减去就行了
=9 - INDEX(REGEXP(H136, "\d", 0), 2)
最后结果
=INDEX(
INDIRECT(
"'Sheet (of Paper)'!" & G136
) :
OFFSET(
INDIRECT(
"'Sheet (of Paper)'!" &
G136
),
8,
8
),
INDEX(REGEXP(H136, "\d", 0), 1),
9 - INDEX(REGEXP(H136, "\d", 0), 2)
)第四题
看起来很麻烦,通过左上角单元格定位,规定size大小的一个nxn的块,然后通过Direction的方向进行对折,最后获取到Reference列对应的值
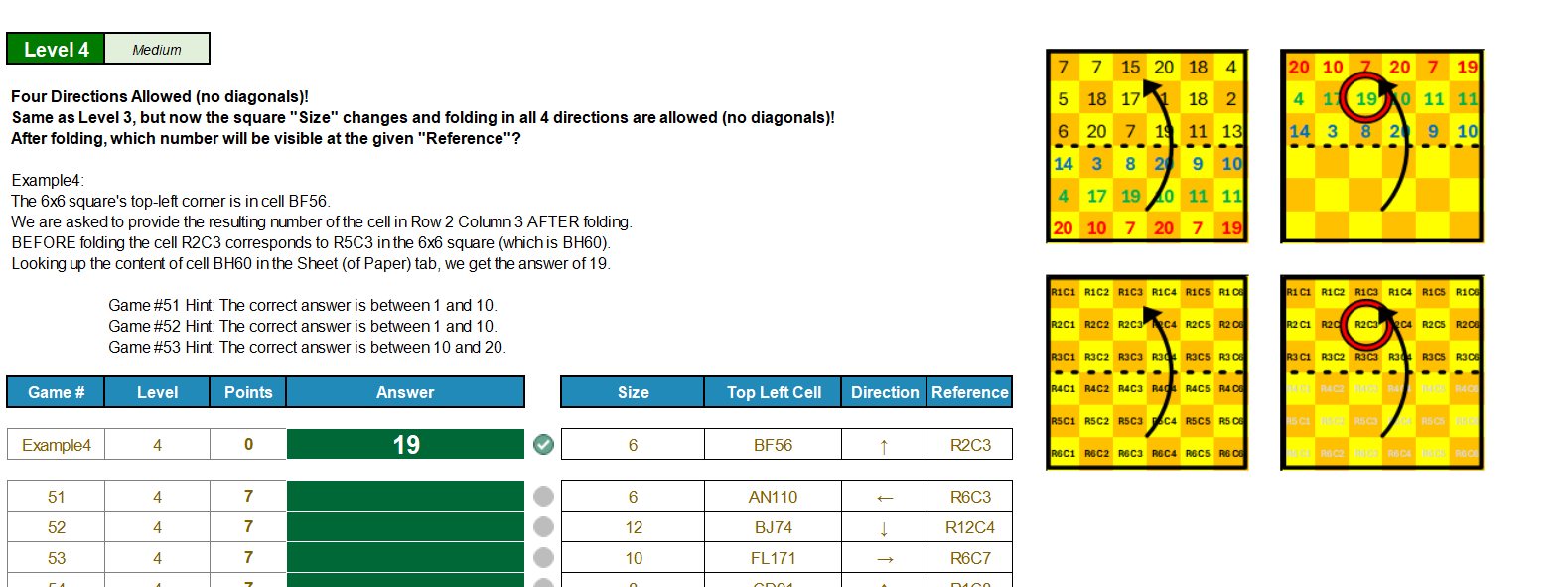
size通过offset解决
左上角通过INDIRECT定位
现在问题是对折的方向然后对解析到R或者C进行判断
我的第一反应是通过IFS进行4向判断单独处理
4向判断
=IFS(
I178 = "↑",
1,
I178 = "↓",
2,
I178 = "←",
3,
I178 = "→",
4
)
再次观察到不应该先判断4向,应该先通过size和左上角定位nxn块
先获取到nxn块
INDIRECT(H178):OFFSET(INDIRECT(H178),G178,G178)有点复杂,引入辅助列
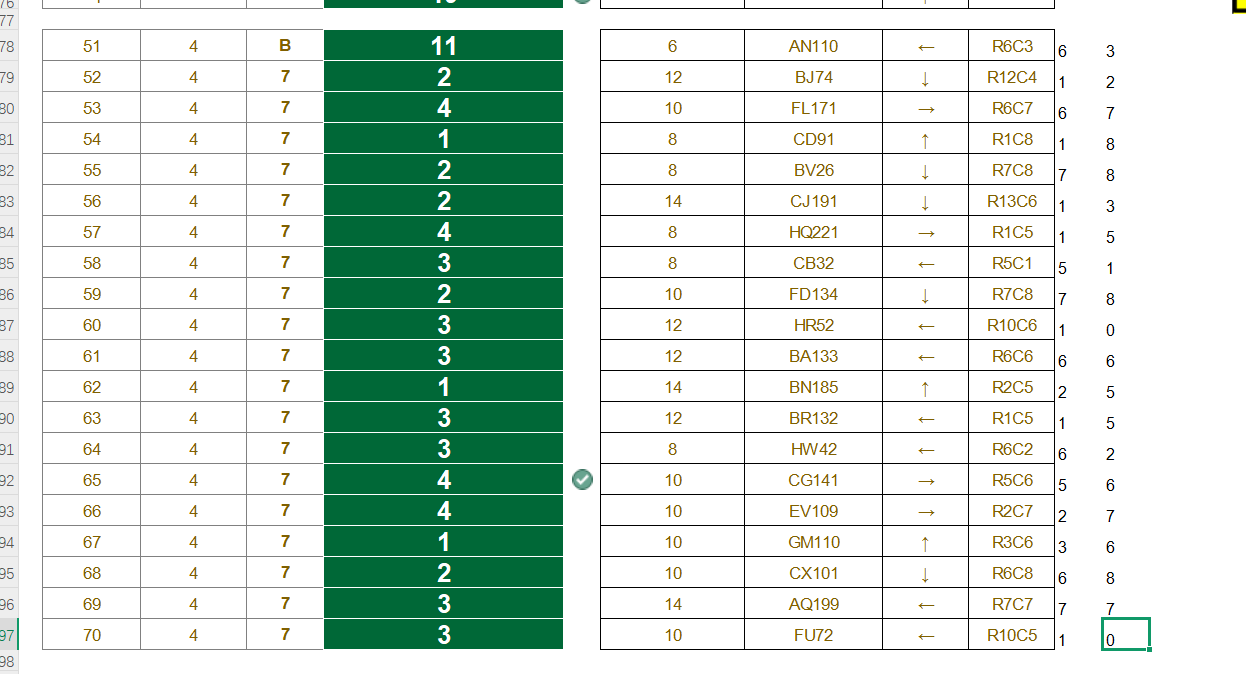
观察到RC已经要超过2位数了,正则改成"\d+"
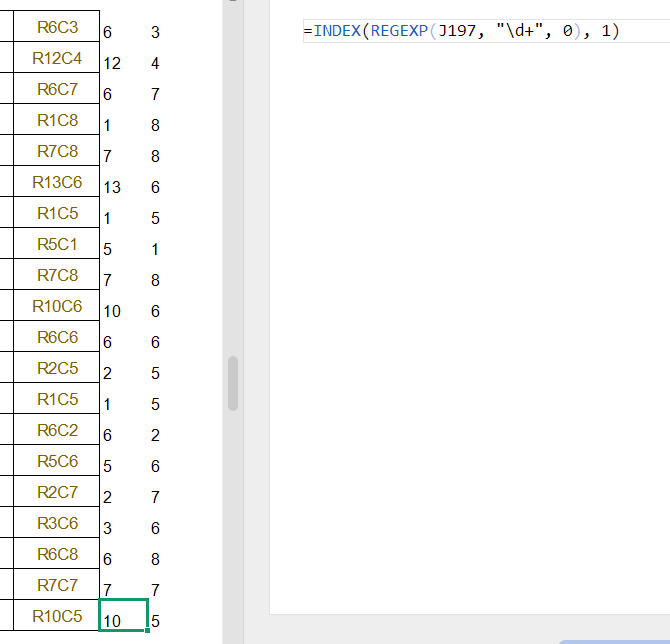
计算对折后的R或者C,
假设size为8
往上对折,C不变,R映射关系为12345678对应87655678,MAX(val,9-val)
往下对折,C不变,R映射关系为12345678对应12344321,MIN(val,9-val)
同理当左右对折时,R也是如此
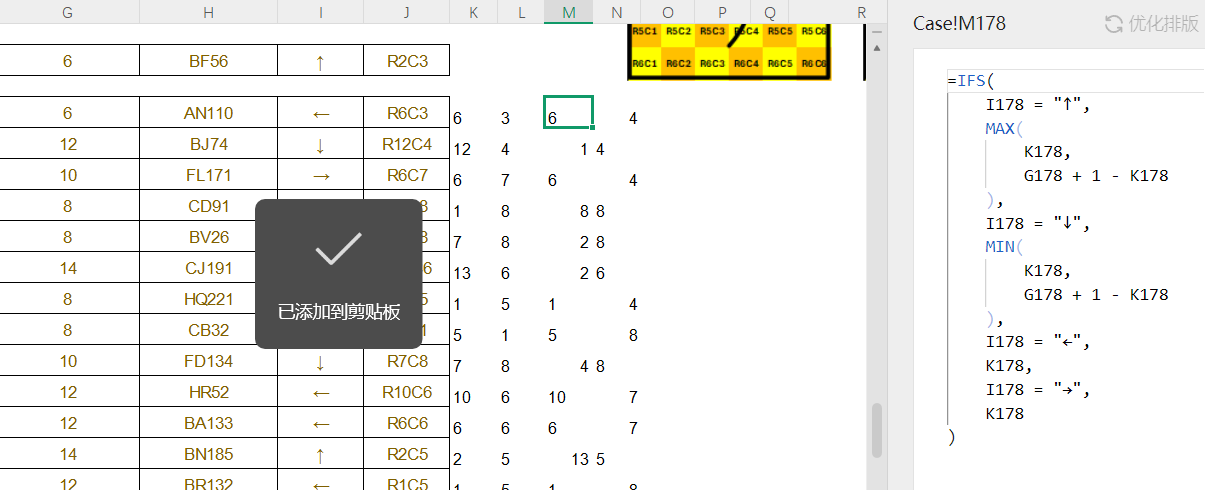
R的转换
=IFS(
I178 = "↑",
MAX(
K178,
G178 + 1 - K178
),
I178 = "↓",
MIN(
K178,
G178 + 1 - K178
),
I178 = "←",
K178,
I178 = "→",
K178
)C的转换
=IFS(
I178 = "←",
MAX(
L178,
G178 + 1 - L178
),
I178 = "→",
MIN(
L178,
G178 + 1 - L178
),
I178 = "↑",
L178,
I178 = "↓",
L178
)最后获取就简单了
=INDEX(
INDIRECT(
"'Sheet (of Paper)'!"
& H178
) :
OFFSET(
INDIRECT(
"'Sheet (of Paper)'!"
& H178
),
G178,
G178
),
M178,
N178
)第五题
和第四题一样就是增加了两次对折

第一印象应该是就是多加一些辅助列即可,解析Directions,然后进行两次转换,观察到这不是传统的对折,而只是简单的对称。因此两个更换顺序是无影响的
引入辅助列直接成功了
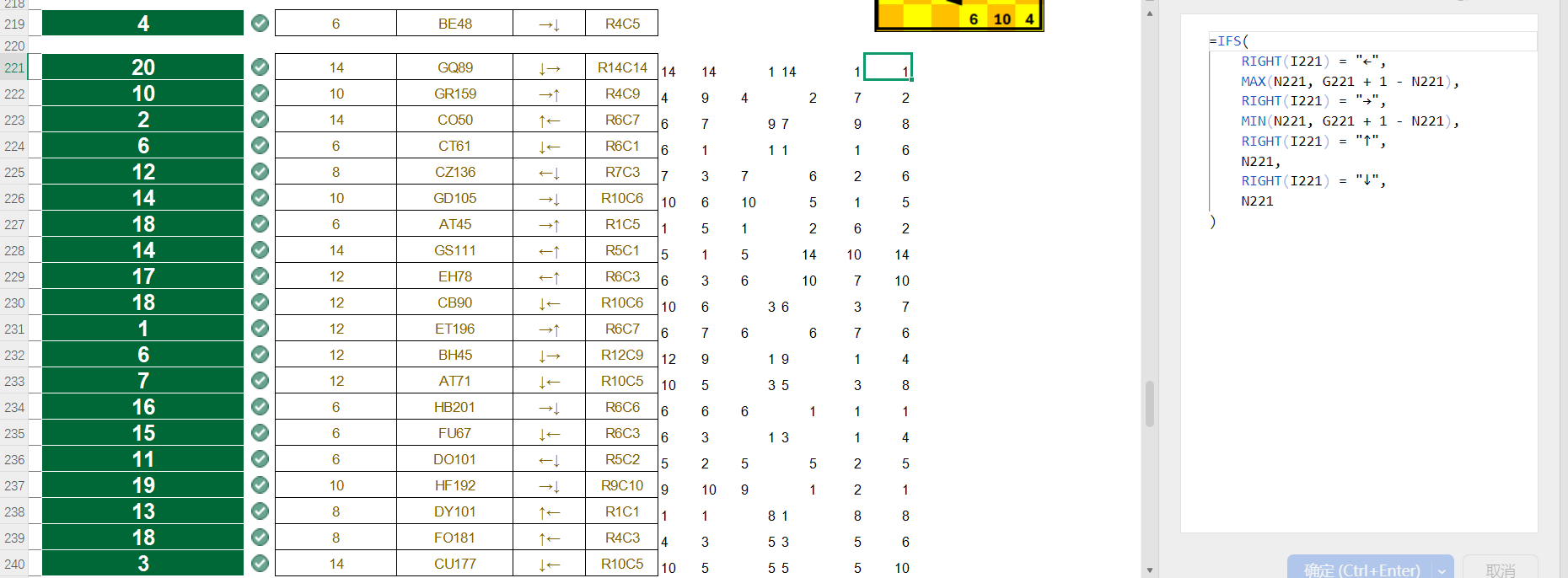
第六题
通过一个Direction斜向对折,然后获取到对应Quadrant1/4块的求和
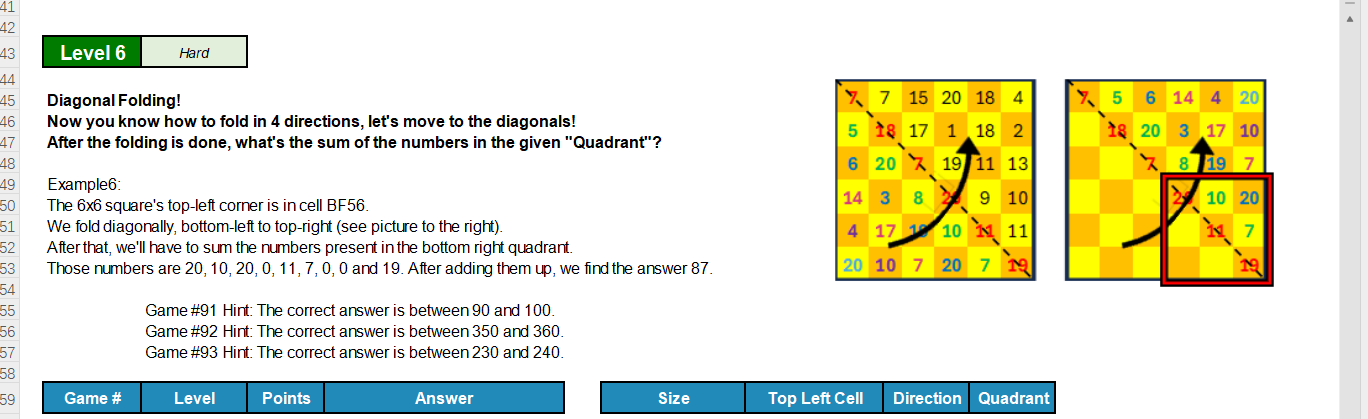
Excel处理行列有点麻烦,不知道怎么写个循环
观察当对折方向和取值方向相同时直接取原始块的(n/2)x(n/2)块的求和即可(最简单)
当方向相反时没有意义
当方向垂直时,取1/4块的斜向一半的求和
同向的很容易写出来,就是堆砌条件就行了
=IFS(
I266 = J266,
IFS(
I266 = "↘",
SUM(
INDIRECT("'Sheet (of Paper)'!" & H266) :
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
G266 / 2 - 1,
G266 / 2 - 1
)
),
I266 = "↙",
SUM(
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
0,
G266 / 2
) :
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
G266 / 2 - 1,
G266 - 1
)
),
I266 = "↗",
SUM(
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
G266 / 2,
0
) :
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
G266 - 1,
G266 / 2 - 1
)
),
I266 = "↖",
SUM(
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
G266 / 2,
G266 / 2
) :
OFFSET(
INDIRECT("'Sheet (of Paper)'!" & H266),
G266 - 1,
G266 - 1
)
)
),
I266 <> J266,
2
)
垂直方向的很难入手,想了很久,没找到方法,咨询了AI对于半区求和的方法,AI给出的方法就是通过SUM+IF进行判断处理,SUM通过COLUMN和ROW的大小来确定该值是否加上去,同时了解到了LET函数