论文: 《Dynamic Low-Rank Sparse Adaptation for Large Language Models》
背景
大语言模型(LLMs)参数规模呈指数级增长(从数十亿到万亿级),虽提升了任务性能,但带来了极高的存储和计算成本。
传统全参数微调 需更新模型所有参数,显存占用大(如 70B 模型全微调需数十 GB GPU 显存)、训练时间长,普通硬件难以支撑。
模型压缩技术(稀疏化、量化、蒸馏)成为部署关键,其中稀疏化通过修剪冗余参数(保留 10%-25% 非零参数),可直接降低计算量和延迟,适配 CPU、边缘设备等轻量化场景。
什么是稀疏微调
稀疏微调是一种在模型微调过程中引入稀疏性以提升效率的技术,核心在于通过结构化剪枝和参数优化,在保持模型性能的同时减少计算成本。
核心定义与流程
稀疏微调通过有选择地修剪模型中不重要的参数连接(如权重矩阵的行/列块),使模型参数呈现高比例的零值(如75-90%稀疏度)。这一过程通常包含三个步骤:
- 结构化剪枝:系统地删除冗余参数,例如对权重矩阵进行分块修剪,保留规则的零值模式(如每4个参数中保留2个非零值),确保硬件(如NVIDIA Ampere架构GPU)能高效利用稀疏性加速计算。
- 迭代优化:逐步增加稀疏度,同时监测精度变化,在保留预训练知识的前提下最大化稀疏性。
- 任务适配:使用下游任务数据对稀疏模型进行微调,通过梯度更新让剩余参数适应新任务分布,同时利用剪枝的正则化效应防止过拟合。
技术优势与应用场景
- 显著提升推理效率 :
- 稀疏模型在CPU上的推理速度可提升2倍以上,且对精度影响极小。例如,清华大学提出的Sparse-Tuning方法在VIT模型中通过稀疏化标记和密集适配器,将计算量降低至原始模型的62%-70%,同时保持SOTA性能。
- 轻量化部署 :
- 结合量化、蒸馏等技术,稀疏微调可将模型压缩10-100倍,使其更易部署在边缘设备。
关键技术创新
- 动态稀疏化与低秩结合 :
- 最新方法如LoSA将低秩矩阵融入稀疏模型,根据稀疏权重动态调整低秩结构,同时利用表征互信息确定各层稀疏率,进一步优化性能。
- 梯度稀疏性利用 :
- 预训练模型的梯度在下游任务中呈现稀疏特性(如1%参数主导梯度),SIFT等方法直接利用这一特性,通过选择性更新参数实现高效微调。
- 硬件协同优化 :
- 结构化剪枝需与硬件架构(如GPU的稀疏计算单元)配合,定制计算内核以充分发挥稀疏性优势。
LoSA论文的研究背景与动机 是围绕大模型"高效微调+轻量化部署"的核心矛盾展开的,具体可分为背景与动机两部分:
一、研究背景
随着大语言模型(LLMs)参数规模扩展到万亿级别,全参数微调的成本过高 ,因此**参数高效微调(PEFT)和模型压缩(如稀疏化)**成为主流方案,但两者结合时存在显著缺陷:
- 稀疏化的局限 :
稀疏方法(如SparseGPT、Wanda)能大幅降低模型大小和推理延迟,但高稀疏率(75%-90%)下性能会严重退化,需要额外微调恢复精度。 - 低秩适配(LoRA)的局限 :
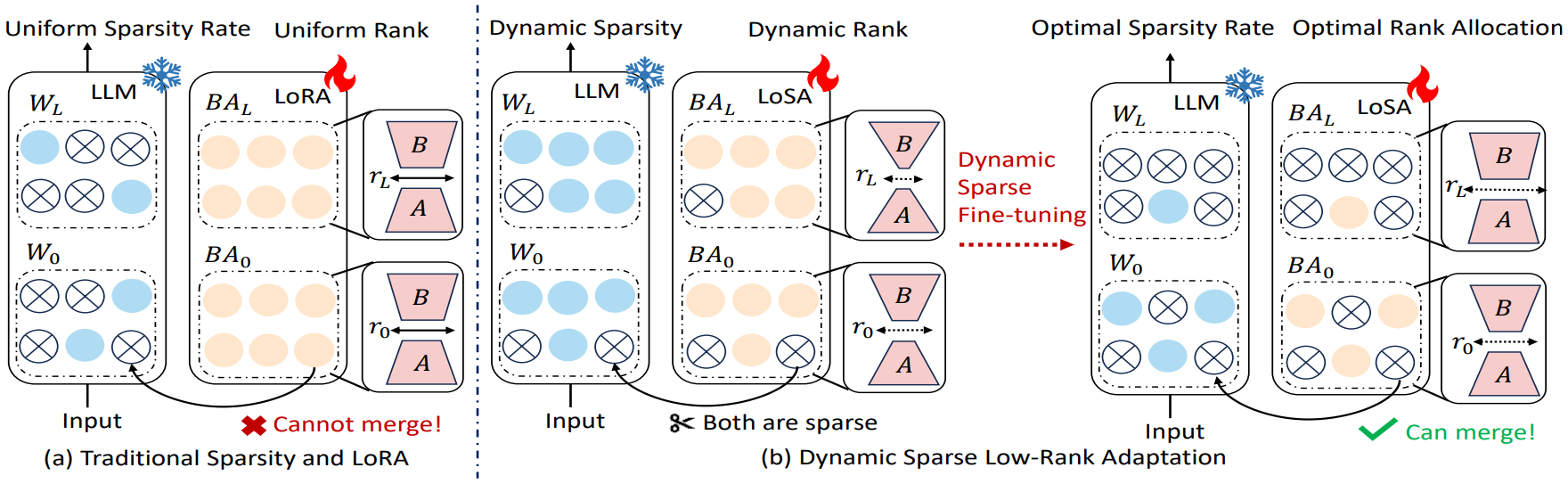
LoRA是经典的PEFT方法,但无法与稀疏模型无缝融合 ------微调后的LoRA低秩矩阵需额外加载,导致推理延迟增加;同时LoRA采用静态秩+均匀稀疏率,未利用模型各层的差异,限制了性能恢复。
二、LoSA论文动机
LoSA的核心动机是解决"稀疏模型+低秩适配"结合时的两大痛点,实现"高效微调+轻量化推理"的统一:
-
痛点1:稀疏与低秩的兼容性问题
传统LoRA的低秩矩阵无法融入稀疏模型权重,导致推理时需同时处理稀疏权重和低秩模块,增加延迟与内存开销,无法发挥稀疏模型的轻量化优势。
→ 动机1 :将低秩矩阵无缝融入稀疏模型结构,避免额外推理负担。
-
痛点2:高稀疏率下的性能损失问题
高稀疏率下直接微调稀疏模型会出现精度下降,而现有方法的静态秩、均匀稀疏率未适配各层的重要性差异,无法高效恢复性能。
→ 动机2 :通过动态调整稀疏率+自适应秩分配,在高稀疏率下恢复模型性能,同时控制参数成本。
为什么传统LoRA的低秩矩阵无法融入稀疏模型权重
一、先搞懂:传统LoRA和稀疏模型各自的"底层规则"
1. 传统LoRA的工作原理(核心是"外挂式"参数更新)
LoRA(Low-Rank Adaptation)是为解决全参数微调成本高而设计的,它的核心逻辑是不修改原模型权重,只新增两个小的低秩矩阵:
- 假设原模型某层权重为 W ∈ R d × d W \in \mathbb{R}^{d \times d} W∈Rd×d( d d d 是隐藏层维度,比如4096);
- LoRA 新增两个低秩矩阵 A ∈ R d × r A \in \mathbb{R}^{d \times r} A∈Rd×r 和 B ∈ R r × d B \in \mathbb{R}^{r \times d} B∈Rr×d( r r r 是秩,远小于 d d d,比如 r = 8 / 16 r=8/16 r=8/16);
- 推理时的最终输出为: h = x W + x A B h = xW + xAB h=xW+xAB( x x x 是输入)。
简单说:LoRA的低秩矩阵 A B AB AB 是 "外挂"在原权重 W W W 上的增量 ,而非直接修改 W W W 本身。
2. 稀疏模型的核心特性(核心是"固定的零值结构")
稀疏模型是对原权重 W W W 做了结构化剪枝 ,最终得到稀疏权重 W sparse = W ⊙ M W_{\text{sparse}} = W \odot M Wsparse=W⊙M( M M M 是掩码矩阵,0=剪枝/1=保留):
- 稀疏模型的核心价值是:大量零值参数无需存储/计算,硬件(如GPU)可通过稀疏加速指令直接跳过零值运算,降低延迟;
- 稀疏模型的关键约束: W sparse W_{\text{sparse}} Wsparse 的零值位置是固定且规则的(比如每4行保留1行),一旦破坏这个结构,硬件就无法识别稀疏性,加速效果直接失效。
二、核心冲突:为什么LoRA的低秩矩阵"融不进去"?
传统LoRA和稀疏模型结合时,会出现两个无法调和的问题,本质是"外挂增量"和"固定稀疏结构"的矛盾:
问题1:低秩矩阵无法与稀疏权重合并,只能"外挂"
如果想把LoRA的增量 A B AB AB 融入稀疏权重 W sparse W_{\text{sparse}} Wsparse,理论上需要做:
W new = W sparse + A B W_{\text{new}} = W_{\text{sparse}} + AB Wnew=Wsparse+AB
但实际中完全不可行:
- W sparse W_{\text{sparse}} Wsparse 有大量零值位置(比如75%稀疏率=75%零值),而 A B AB AB 是稠密矩阵(几乎无零值);
- 合并后 W new W_{\text{new}} Wnew 的零值结构被完全破坏(原本的零值位置被 A B AB AB 的非零值填充),稀疏模型的硬件加速优势直接消失,相当于白做了稀疏化。
因此传统做法只能保留" h = x W sparse + x A B h = xW_{\text{sparse}} + xAB h=xWsparse+xAB"的形式------低秩矩阵必须单独存储、单独计算,无法融入稀疏权重。
问题2:额外计算增加推理延迟,违背稀疏化的初衷
稀疏化的核心目标是降低推理延迟,但"外挂"LoRA的低秩矩阵会带来两个额外开销:
- 存储开销 :需要额外存 A A A 和 B B B 两个矩阵(虽然小,但会抵消部分稀疏化的存储收益);
- 计算开销 :推理时要多算一次 x A B xAB xAB,且 A B AB AB 是稠密计算(无稀疏加速),最终导致整体推理延迟反而比纯稀疏模型更高。
三、通俗总结
你可以把稀疏模型想象成"一栋被拆了冗余房间的房子(零值=拆了的房间),只剩必要房间(非零值),走路(计算)更快";
传统LoRA的低秩矩阵是"在房子外搭了个临时小屋(外挂增量),虽然小,但每次走路都要先绕小屋,反而变慢";
而"融不进去"的核心是:如果把临时小屋的东西搬进主屋,会把主屋原本拆空的房间又填满(破坏稀疏结构),主屋的走路优势就没了。
这也是LoSA要解决的核心问题 :让低秩矩阵的稀疏模式和原模型的稀疏模式对齐 ,既能合并进稀疏权重,又不破坏零值结构,最终实现" h = x ( W sparse + A B sparse ) h = x(W_{\text{sparse}} + AB_{\text{sparse}}) h=x(Wsparse+ABsparse)",且 W sparse + A B sparse W_{\text{sparse}} + AB_{\text{sparse}} Wsparse+ABsparse 仍保持稀疏特性。
总结
- 传统LoRA的低秩矩阵是外挂式增量,而非对原权重的直接修改;
- 稀疏模型的核心价值是固定的零值结构,一旦破坏就失去加速效果;
- 若将LoRA的稠密低秩矩阵融入稀疏权重,会破坏零值结构;若不融入,则需额外计算,违背稀疏化降延迟的初衷------这就是"无法融入"的本质。