上
.线性模型简介
\;\;\;\;\;\;\;\; 线性模型指的是通过属性的线性 组合进行预测的函数模型。具体形式如下:
f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b \boldsymbol{f(x)=w_1x_1+w_2x_2+...+w_dx_d+b} f(x)=w1x1+w2x2+...+wdxd+b
写成向量的形式就是:
f ( x ) = w T x + b \boldsymbol{f(x)=w ^Tx+b} f(x)=wTx+b
其中, w = ( w 1 ; w 2 ; . . . ; w d ) \boldsymbol{w=(w_{1};w_{2};...;w_{d})} w=(w1;w2;...;wd) 和 b \boldsymbol{b} b 是权重向量(权重 w \boldsymbol{w} w 直观反映各属性的重要性), x = ( x 1 ; x 2 ; . . . ; x d ) \boldsymbol{x=(x_{1};x_{2};...;x_{d})} x=(x1;x2;...;xd) 是一个示例的 d 个属性。
\;\;\;\;\;\;\;\; 由于线性模型可解释性强,可以通过线性模型引入更多复杂的模型,他们依赖于最基础的线性模型解释逻辑。
.线性回归
\;\;\;\;\;\;\;\; 定义 :给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ... , ( x m , y m ) } \boldsymbol{D} = \{ (\boldsymbol{x}_1, \boldsymbol{y}_1), (\boldsymbol{x}_2, \boldsymbol{y}_2), \dots, (\boldsymbol{x}m, \boldsymbol{y}m) \} D={(x1,y1),(x2,y2),...,(xm,ym)},其中 x i = ( x i 1 , x i 2 , ... , x i d ) , y i ∈ R \boldsymbol{x}i = (\boldsymbol{x}{i1}, \boldsymbol{x}{i2}, \dots, \boldsymbol{x}{id}) ,\boldsymbol{y}_i \in \mathbb{R} xi=(xi1,xi2,...,xid),yi∈R。"线性回归"(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记。(多元线性回归 ,如果 x i \boldsymbol{x}_i xi只有一个属性,那么称作单元线性回归)
\;\;\;\;\;\;\;\; 离散属性处理规则:有序属性(如 "高 / 中 / 低")可连续化为数值(1.0/0.5/0.0);无序属性(如 "西瓜 / 南瓜 / 黄瓜")需转化为 k 维向量((0,0,1)/(0,1,0)/(1,0,0)),避免引入不当序关系。(个人想法:无序属性是否可以通过更底层的关联性转换为有序关系?)
\;\;\;\;\;\;\;\; 简单说,线性回归要干的事情就是让训练出来的模型的预测值与真实值越小越好 ,下面是单元线性回归 ❗️❗️(单元和多元都会介绍,先介绍单元的):
f ( x i ) = w x i + b \boldsymbol{f(x_i)=wx_i+b} f(xi)=wxi+b
x i \boldsymbol{x}_i xi为单个输入属性值, w \boldsymbol{w} w 为权重, b \boldsymbol{b} b 为偏置项,目标是让 f ( x i ) ≃ y i \boldsymbol{f(x_i) \simeq y_i} f(xi)≃yi ( y i \boldsymbol{y}_i yi 为真实输出标记)。目标值 f ( x i ) \boldsymbol{f(x_i)} f(xi)和输入 x i \boldsymbol{x}_i xi已知,所以训练模型实际上就是找到最优的 w \boldsymbol{w} w 和 b \boldsymbol{b} b。下面说怎么找到这两个参数。
...最小二乘法
\;\;\;\;\;\;\;\; 通过最小化均方误差(平方损失)确定最优参数 w ∗ \boldsymbol{w^*} w∗ 和 b ∗ \boldsymbol{b^*} b∗:
( w ∗ , b ∗ ) = arg min ( w , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 = arg min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 \begin{aligned} \boldsymbol{(w^*, b^*)} &= \boldsymbol{\underset{(w, b)}{\arg\min} \sum_{i=1}^m \left(f(x_i) - y_i\right)^2} \\ &= \boldsymbol{\underset{(w, b)}{\arg\min} \sum_{i=1}^m \left(y_i - w x_i - b\right)^2} \end{aligned} (w∗,b∗)=(w,b)argmini=1∑m(f(xi)−yi)2=(w,b)argmini=1∑m(yi−wxi−b)2
求解 w \boldsymbol{w} w 和 b \boldsymbol{b} b 使 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 \boldsymbol{E_{(w,b)}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^2} E(w,b)=∑i=1m(yi−wxi−b)2 最小化的过程,称为线性回归模型的最小二乘 "参数估计" 。如何求解 w \boldsymbol{w} w, b \boldsymbol{b} b最优解?
首先介绍一下凸函数💡
...凸函数
对区间 [ a , b ] \boldsymbol{[a, b]} [a,b]上定义 的函数 f \boldsymbol{f} f ,若它对区间中任意两点 x 1 , x 2 \boldsymbol{x_{1} , x_{2}} x1,x2
均有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 \boldsymbol{f(\frac{x_{1}+x_{2}}{2}) ≤\frac{f(x_{1})+f(x_{2})}{2}} f(2x1+x2)≤2f(x1)+f(x2),则称 f \boldsymbol{f} f 为区间 [ a , b ] \boldsymbol{[a, b]} [a,b]上的凸函数。
比如 f ( x ) = x 2 \boldsymbol{f(x)=x^{2}} f(x)=x2是凸函数,从导数的角度出发,若 f \boldsymbol{f} f 在区间中二阶导数非负,那么 f \boldsymbol{f} f 是凸函数,并且有全局最小值,且其最小值就是当一阶导数为0的点。
...单元线性回归
回到公式: E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 \boldsymbol{E_{(w,b)}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^2} E(w,b)=∑i=1m(yi−wxi−b)2
未知量是: w \boldsymbol{w} w, b \boldsymbol{b} b。那么分别对 w \boldsymbol{w} w, b \boldsymbol{b} b求偏导得到:
∂ E ( w , b ) ∂ w = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) ( 1 ) \boldsymbol{\frac{\partial E_{(w, b)}}{\partial w} = 2\left(w \sum_{i=1}^m x_i^2 - \sum_{i=1}^m \left(y_i - b\right) x_i\right)} (1) ∂w∂E(w,b)=2(wi=1∑mxi2−i=1∑m(yi−b)xi)(1)
∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) ( 2 ) \boldsymbol{\frac{\partial E_{(w, b)}}{\partial b} = 2\left(m b - \sum_{i=1}^m \left(y_i - w x_i\right)\right)}(2) ∂b∂E(w,b)=2(mb−i=1∑m(yi−wxi))(2)
令(1),(2)分别为0。
2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) = 0 \boldsymbol{2\left(w \sum_{i=1}^m x_i^2 - \sum_{i=1}^m \left(y_i - b\right) x_i\right) =0} 2(wi=1∑mxi2−i=1∑m(yi−b)xi)=0
w ∑ i = 1 m x i 2 = ∑ i = 1 m ( y i − b ) x i \boldsymbol{w \sum_{i=1}^m x_i^2 = \sum_{i=1}^m \left(y_i - b\right) x_i} wi=1∑mxi2=i=1∑m(yi−b)xi
w = ∑ i = 1 m ( y i − b ) x i ∑ i = 1 m x i 2 ( 3 ) \boldsymbol{w = \frac{\sum_{i=1}^m \left(y_i - b\right)x_i}{\sum_{i=1}^m x_i^2}} \;\;\;\;\;\;\;\; (3) w=∑i=1mxi2∑i=1m(yi−b)xi(3)
到这里发现不能化简了,需要对(2)式进行化简。
2 ( m b − ∑ i = 1 m ( y i − w x i ) ) = 0 \boldsymbol{2\left(m b - \sum_{i=1}^m \left(y_i - w x_i\right)\right)=0} 2(mb−i=1∑m(yi−wxi))=0
b = 1 m ∑ i = 1 m ( y i − w x i ) \boldsymbol{b =\frac{1}{m} \sum_{i=1}^m \left(y_i - w x_i\right)} b=m1i=1∑m(yi−wxi)
将 b \boldsymbol{b} b 带入(3)式,得到:
w = ∑ i = 1 m ( y i − 1 m ∑ i = 1 m ( y i − w x i ) ) x i ∑ i = 1 m x i 2 ( 4 ) \boldsymbol{w = \frac{\sum_{i=1}^m \left(y_i - \frac{1}{m} \sum_{i=1}^m \left(y_i - w x_i\right)\right)x_i}{\sum_{i=1}^m x_i^2}} (4) w=∑i=1mxi2∑i=1m(yi−m1∑i=1m(yi−wxi))xi(4)
看起来比较复杂,所以为了简化公式,令 y ‾ = 1 m ∑ i = 1 m y i , x ‾ = 1 m ∑ i = 1 m x i \boldsymbol{\overline{y} = \frac{1}{m}\sum_{i=1}^m y_i , \overline{x} = \frac{1}{m}\sum_{i=1}^m x_i} y=m1i=1∑myi,x=m1i=1∑mxi
则(4)化简为:
w = ∑ i = 1 m ( y i − y ‾ + w x ‾ ) x i ∑ i = 1 m x i 2 \boldsymbol{w = \frac{\sum_{i=1}^m \left(y_i - \overline{y}+w\overline{x}\right)x_i}{\sum_{i=1}^m x_i^2}} w=∑i=1mxi2∑i=1m(yi−y+wx)xi
w ∑ i = 1 m x i 2 = ∑ i = 1 m ( y i − y ‾ + w x ‾ ) x i = ∑ i = 1 m x i y i − m x ‾ y ‾ + m w x ‾ 2 \boldsymbol{w {\sum_{i=1}^m x_i^2}= {\sum_{i=1}^m \left(y_i - \overline{y}+w\overline{x}\right)x_i}={\sum_{i=1}^mx_iy_i-m\overline{x} \overline{y}+mw\overline{x}^2}} wi=1∑mxi2=i=1∑m(yi−y+wx)xi=i=1∑mxiyi−mxy+mwx2
将含 w \boldsymbol{w} w项都放到左边得:
w ∑ i = 1 m x i 2 − m w x ‾ 2 = ∑ i = 1 m x i y i − m x ‾ y ‾ \boldsymbol{w {\sum_{i=1}^m x_i^2}-mw\overline{x}^2={\sum_{i=1}^mx_iy_i-m\overline{x} \overline{y}}} wi=1∑mxi2−mwx2=i=1∑mxiyi−mxy
将 w \boldsymbol{w} w提取出来得到:
w ( ∑ i = 1 m x i 2 − m x ‾ 2 ) = ∑ i = 1 m x i y i − m x ‾ y ‾ \boldsymbol{w( {\sum_{i=1}^m x_i^2}-m\overline{x}^2)={\sum_{i=1}^mx_iy_i-m\overline{x} \overline{y}}} w(i=1∑mxi2−mx2)=i=1∑mxiyi−mxy
从而得到:
w = ∑ i = 1 m x i y i − m x ‾ y ‾ ∑ i = 1 m x i 2 − m x ‾ 2 \boldsymbol{w=\frac{\sum_{i=1}^mx_iy_i-m\overline{x} \overline{y}}{{\sum_{i=1}^m x_i^2}-m\overline{x}^2}} w=∑i=1mxi2−mx2∑i=1mxiyi−mxy
其等价于:
w = ∑ i = 1 m y i ( x i − x ‾ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 \boldsymbol{w=\frac{\sum_{i=1}^my_i(x_i-\overline{x}) }{{\sum_{i=1}^m x_i^2}-\frac{1}{m}(\sum_{i=1}^mx_i)^2}} w=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x)
从而 w \boldsymbol{w} w得闭式解就可以求出来。且 b = 1 m ∑ i = 1 m ( y i − w x i ) \boldsymbol{b =\frac{1}{m} \sum_{i=1}^m \left(y_i - w x_i\right)} b=m1i=1∑m(yi−wxi)
将 w \boldsymbol{w} w的表达式带入 b \boldsymbol{b} b即可得到 b \boldsymbol{b} b。发现,由 w \boldsymbol{w} w开始化简,然后将 b \boldsymbol{b} b带入 w \boldsymbol{w} w得到关于 w \boldsymbol{w} w的等式,最后得到关于 w \boldsymbol{w} w的表达式。那么同理,由 b \boldsymbol{b} b开始化简,然后将 w \boldsymbol{w} w带入 b \boldsymbol{b} b得到关于 b \boldsymbol{b} b的等式,可以得到关于 b \boldsymbol{b} b的表达式。两个推导都一样。💡💡
\;\;\;\;\;\;\;\; 上面说到,这个公式推导式单元线性回归,也就是说,样本的属性数量只有一个。但是日常更加常见的情况是多元线性回归 ,即一个样本有多个属性 组成,比如西瓜=[绿色,根长,条纹多,圆形]。
\;\;\;\;\;\;\;\; 因此,对于多元线性回归模型,我们要学习的是:
f ( x i ) = w T x i + b , 使得 f ( x i ) ≃ y i \boldsymbol{f(\boldsymbol{x}_i) = \boldsymbol{w}^T \boldsymbol{x}_i + b, \quad \text{使得 } f(\boldsymbol{x}_i) \simeq y_i} f(xi)=wTxi+b,使得 f(xi)≃yi
...多元线性回归
w = ( w 1 ; w 2 ; . . . ; w d ) \boldsymbol{w} = (\boldsymbol{w}1; \boldsymbol{w}2; ...; \boldsymbol{w}d) w=(w1;w2;...;wd):d 维列向量(分号表示纵向拼接),对应 d 个输入属性的权重;
x i = ( x i 1 ; x i 2 ; . . . ; x i d ) \boldsymbol{x}i = (\boldsymbol{x}{i1}; \boldsymbol{x}{i2}; ...; \boldsymbol{x}{id}) xi=(xi1;xi2;...;xid):第 i 个样本的 d 维列向量(对应 d 个输入属性的取值);
w T x i = w 1 x i 1 + w 2 x i 2 + . . . + w d x i d \boldsymbol{w}^T \boldsymbol{x}i = \boldsymbol{w_1x{i1} + w_2x{i2} + ... + w_dx_{id}} wTxi=w1xi1+w2xi2+...+wdxid:向量内积(本质是 d 个属性的线性组合);
b \boldsymbol b b:标量偏置项(与输入属性无关的基准值)。
w T x i \boldsymbol{w}^T \boldsymbol{x}_i wTxi 是 "向量运算", + b \boldsymbol{+b} +b 是 "标量加法",形式不统一,无法直接用矩阵批量处理 所有样本。因此,把 "向量内积 + 标量" 的混合形式,转化为纯向量内积,统一运算规则。
将 w \boldsymbol{w} w 和 b \boldsymbol{b} b 整合为 w ^ = ( w ; b ) \boldsymbol{\hat{\boldsymbol{w}} = (\boldsymbol{w}; b)} w^=(w;b) ,把标量偏置 b \boldsymbol{b} b 作为 "第 d + 1 \boldsymbol{d+1} d+1 个权重",与原权重向量 w \boldsymbol{w} w 纵向拼接,形成 d + 1 \boldsymbol{d+1} d+1维列向量 w ^ \boldsymbol{\hat{\boldsymbol{w}}} w^:
w ^ = ( w ; b ) = ( w 1 w 2 ⋮ w d b ) \boldsymbol{\hat{\boldsymbol{w}} = (\boldsymbol{w}; b) = \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_d \\ b \end{pmatrix}} w^=(w;b)= w1w2⋮wdb
为了匹配 w ^ \boldsymbol{\hat{\boldsymbol{w}}} w^ 的 d + 1 \boldsymbol{d+1} d+1 维,需要给每个样本 x i \boldsymbol{x}_i xi 补充一个 "常数项 1",形成扩展样本向量。
x ^ i = ( x i ; 1 ) = ( x i 1 x i 2 ⋮ x i d 1 ) \boldsymbol{\hat{\boldsymbol{x}}i = (\boldsymbol{x}i; 1) = \begin{pmatrix} x{i1} \\ x{i2} \\ \vdots \\ x_{id} \\ 1 \end{pmatrix}} x^i=(xi;1)= xi1xi2⋮xid1
此时,多元线性回归模型可简化为: f ( x ^ i ) = x ^ i T w ^ \boldsymbol{f(\hat{\boldsymbol{x}}_i) = \hat{\boldsymbol{x}}_i^T \hat{\boldsymbol{w}}} f(x^i)=x^iTw^
此时,公式内只有向量运算,没有标量运算。实际上就是把标量运算融合进了向量运算中。(跨模态转换)。再拼接所有样本得到矩阵 X \boldsymbol{X} X:
X = ( x 11 x 12 ... x 1 d 1 x 21 x 22 ... x 2 d 1 ⋮ ⋮ ⋱ ⋮ ⋮ x m 1 x m 2 ... x m d 1 ) = ( x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ) , x ^ i = ( x i ; 1 ) = ( x i 1 x i 2 ⋮ x i d 1 ) , X = ( x ^ 1 T x ^ 2 T ⋮ x ^ m T ) \boldsymbol{X} = \boldsymbol{\begin{pmatrix} x_{11} & x_{12} & \dots & x_{1d} & 1 \\ x_{21} & x_{22} & \dots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m1} & x_{m2} & \dots & x_{md} & 1 \end{pmatrix} = \begin{pmatrix} \boldsymbol{x}_1^T & 1 \\ \boldsymbol{x}_2^T & 1 \\ \vdots & \vdots \\ \boldsymbol{x}m^T & 1 \end{pmatrix}}, \boldsymbol{\hat{\boldsymbol{x}}i = (\boldsymbol{x}i; 1) = \begin{pmatrix} x{i1} \\ x{i2} \\ \vdots \\ x{id} \\ 1 \end{pmatrix}}, \boldsymbol{X} = \boldsymbol{\begin{pmatrix} \hat{\boldsymbol{x}}_1^T \\ \hat{\boldsymbol{x}}_2^T \\ \vdots \\ \hat{\boldsymbol{x}}_m^T \end{pmatrix}} X= x11x21⋮xm1x12x22⋮xm2......⋱...x1dx2d⋮xmd11⋮1 = x1Tx2T⋮xmT11⋮1 ,x^i=(xi;1)= xi1xi2⋮xid1 ,X= x^1Tx^2T⋮x^mT
整合后,批量预测(m个样本)的预测值可简化为纯矩阵乘法形式 :
( f ( x ^ 1 ) f ( x ^ 2 ) ⋮ f ( x ^ m ) ) = X w ^ ( 5 ) \boldsymbol{\begin{pmatrix} f(\hat{x}_1) \\ f(\hat{x}_2) \\ \vdots \\ f(\hat{x}_m) \end{pmatrix} = \boldsymbol{X} \hat{\boldsymbol{w}}} (5) f(x^1)f(x^2)⋮f(x^m) =Xw^(5)
多元线性回归的目标是让 "所有样本的预测值与真实值的差异最小",所以目标函数仍然是沿用单变量的均方误差(平方损失)。
目标函数的推导
单变量的均方误差是 "逐个样本误差的平方和": E = ∑ i = 1 m ( y i − f ( x i ) ) 2 \boldsymbol{E = \sum_{i=1}^m (y_i - f(x_i))^2} E=∑i=1m(yi−f(xi))2,推广到多元并转化为矩阵形式
- 误差(残差)向量:所有样本的 "真实值 - 预测值" 构成 m 维列向量 y − X w ^ \boldsymbol{y} - \boldsymbol{X} \hat{\boldsymbol{w}} y−Xw^;
- 均方误差:误差向量的 "转置 × 自身"(向量内积的矩阵表示,结果为标量,即所有误差的平方和): E w ^ = ( y − X w ^ ) T ( y − X w ^ ) \boldsymbol{E_{\hat{\boldsymbol{w}}} = (\boldsymbol{y} - \boldsymbol{X} \hat{\boldsymbol{w}})^T (\boldsymbol{y} - \boldsymbol{X} \hat{\boldsymbol{w}})} Ew^=(y−Xw^)T(y−Xw^)
综上,参数估计目标为找到使 w ^ ∗ = arg min w ^ ( y − X w ^ ) T ( y − X w ^ ) \boldsymbol{\hat{\boldsymbol{w}}^* = \underset{\hat{\boldsymbol{w}}}{\arg\min} (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})^T (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})} w^∗=w^argmin(y−Xw^)T(y−Xw^)
E w ^ = arg min w ^ ( y − X w ^ ) T ( y − X w ^ ) \boldsymbol{E_{\hat{w}}} = \boldsymbol{\underset{\hat{\boldsymbol{w}}}{\arg\min} (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})^T (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})} Ew^=w^argmin(y−Xw^)T(y−Xw^)
先将 E w ^ = ( y − X w ^ ) T ( y − X w ^ ) \boldsymbol{E_{\hat{\boldsymbol{w}}} = (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})^T (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})} Ew^=(y−Xw^)T(y−Xw^) 展开(矩阵乘法分配律):
E w ^ = y T y − y T ( X w ^ ) − ( X w ^ ) T y + ( X w ^ ) T ( X w ^ ) = y T y − 2 w ^ T X T y + w ^ T ( X T X ) w ^ \begin{aligned} \boldsymbol{E_{\hat{\boldsymbol{w}}}} &= \boldsymbol{y}^T \boldsymbol{y} - \boldsymbol{y}^T (\boldsymbol{X}\hat{\boldsymbol{w}}) - (\boldsymbol{X}\hat{\boldsymbol{w}})^T \boldsymbol{y} + (\boldsymbol{X}\hat{\boldsymbol{w}})^T (\boldsymbol{X}\hat{\boldsymbol{w}}) \\ &= \boldsymbol{y}^T \boldsymbol{y} - 2\hat{\boldsymbol{w}}^T \boldsymbol{X}^T \boldsymbol{y} + \hat{\boldsymbol{w}}^T (\boldsymbol{X}^T \boldsymbol{X}) \hat{\boldsymbol{w}} \end{aligned} Ew^=yTy−yT(Xw^)−(Xw^)Ty+(Xw^)T(Xw^)=yTy−2w^TXTy+w^T(XTX)w^
- 关键简化:
y T ( X w ^ ) = ( X w ^ ) T y = w ^ T X T y \boldsymbol{y}^T (\boldsymbol{X}\hat{\boldsymbol{w}}) = (\boldsymbol{X}\hat{\boldsymbol{w}})^T \boldsymbol{y} = \hat{\boldsymbol{w}}^T \boldsymbol{X}^T \boldsymbol{y} yT(Xw^)=(Xw^)Ty=w^TXTy
因此合并为 − 2 w ^ T X T y \boldsymbol{-2\hat{\boldsymbol{w}}^T \boldsymbol{X}^T \boldsymbol{y}} −2w^TXTy。
应用矩阵求导规则求偏导
矩阵求导的核心规则(针对列向量 w ^ \boldsymbol{\hat{\boldsymbol{w}}} w^):
-
常数项的导数: ∂ ( y T y ) ∂ w ^ = 0 \boldsymbol{\frac{\partial (\boldsymbol{y}^T \boldsymbol{y})}{\partial \hat{\boldsymbol{w}}} = \boldsymbol{0}} ∂w^∂(yTy)=0
-
线性项的导数: ∂ ( w ^ T A ) ∂ w ^ = A \boldsymbol{\frac{\partial (\hat{\boldsymbol{w}}^T \boldsymbol{A})}{\partial \hat{\boldsymbol{w}}} = \boldsymbol{A}} ∂w^∂(w^TA)=A(此处 A = X T y \boldsymbol{A} = \boldsymbol{X}^T \boldsymbol{y} A=XTy),因此
∂ ( − 2 w ^ T X T y ) ∂ w ^ = − 2 X T y \boldsymbol{\frac{\partial (-2\hat{\boldsymbol{w}}^T \boldsymbol{X}^T \boldsymbol{y})}{\partial \hat{\boldsymbol{w}}} = -2\boldsymbol{X}^T \boldsymbol{y}} ∂w^∂(−2w^TXTy)=−2XTy -
二次项的导数: ∂ ( w ^ T B w ^ ) ∂ w ^ = 2 B w ^ \boldsymbol{\frac{\partial (\hat{\boldsymbol{w}}^T \boldsymbol{B}\hat{\boldsymbol{w}})}{\partial \hat{\boldsymbol{w}}} = 2\boldsymbol{B}\hat{\boldsymbol{w}}} ∂w^∂(w^TBw^)=2Bw^(此处 B = X T X \boldsymbol{B} = \boldsymbol{X}^T \boldsymbol{X} B=XTX),因此
∂ ( w ^ T X T X w ^ ) ∂ w ^ = 2 X T X w ^ \boldsymbol{\frac{\partial (\hat{\boldsymbol{w}}^T \boldsymbol{X}^T \boldsymbol{X}\hat{\boldsymbol{w}})}{\partial \hat{\boldsymbol{w}}} = 2\boldsymbol{X}^T \boldsymbol{X}\hat{\boldsymbol{w}}} ∂w^∂(w^TXTXw^)=2XTXw^
合并上面三项得到:
∂ ( E w ^ ) ∂ w ^ = 0 − 2 X T y + 2 X T X w ^ = 2 X T ( X w ^ − y ) ( 6 ) \boldsymbol{\frac{\partial \boldsymbol{(E_{\hat w})}}{\partial \hat{\boldsymbol{w}}} = \boldsymbol0-2\boldsymbol{X^Ty+2X^TX{\hat w}}=\boldsymbol{2X^T(X{\hat w}-y)}} \;\;\;\;\;\;(6) ∂w^∂(Ew^)=0−2XTy+2XTXw^=2XT(Xw^−y)(6)
令导数 ∂ ( E w ^ ) ∂ w ^ \boldsymbol{\frac{\partial \boldsymbol{(E_{\hat w})}}{\partial \hat{\boldsymbol{w}}}} ∂w^∂(Ew^)等于0
X T X w ^ = X T y \boldsymbol{X^TX{\hat w}=X^Ty} XTXw^=XTy
要求出 w ^ \boldsymbol{{\hat w}} w^,等式左右两边同时乘上 ( X T X ) − 1 \boldsymbol{(X^TX)^{-1}} (XTX)−1。当然了,前提是 ( X T X ) \boldsymbol{(X^TX)} (XTX)可逆。这里假设 ( X T X ) \boldsymbol{(X^TX)} (XTX)是一个实对称矩阵(等价于满秩矩阵,样本数要多于属性数,即行大于列,必需满足各列线性无关),即是可逆矩阵。
w ^ = ( X T X ) − 1 X T y \boldsymbol{{\hat w}=(X^TX)^{-1}X^Ty} w^=(XTX)−1XTy
最后得到的最优解 模型即:
f ( x ^ i ) = x ^ i T ( X T X ) − 1 X T y \boldsymbol{f\left(\hat{x}{i}\right)=\hat{x}{i}^{T}\left(X^{T} X\right)^{-1} X^{T} y} f(x^i)=x^iT(XTX)−1XTy
理性很饱满,现实很骨感,上面的式子虽然是最优解,但是有前提条件,即矩阵 X T X \boldsymbol{X^TX} XTX是满秩矩阵。 X \boldsymbol{X} X即输入数据集合以矩阵的形式表达:
X = ( x 11 x 12 ... x 1 d 1 x 21 x 22 ... x 2 d 1 ⋮ ⋮ ⋱ ⋮ ⋮ x m 1 x m 2 ... x m d 1 ) = ( x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ) , x ^ i = ( x i ; 1 ) = ( x i 1 x i 2 ⋮ x i d 1 ) , X = ( x ^ 1 T x ^ 2 T ⋮ x ^ m T ) \boldsymbol{X} = \boldsymbol{\begin{pmatrix} x_{11} & x_{12} & \dots & x_{1d} & 1 \\ x_{21} & x_{22} & \dots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m1} & x_{m2} & \dots & x_{md} & 1 \end{pmatrix} = \begin{pmatrix} \boldsymbol{x}_1^T & 1 \\ \boldsymbol{x}_2^T & 1 \\ \vdots & \vdots \\ \boldsymbol{x}m^T & 1 \end{pmatrix}}, \boldsymbol{\hat{\boldsymbol{x}}i = (\boldsymbol{x}i; 1) = \begin{pmatrix} x{i1} \\ x{i2} \\ \vdots \\ x{id} \\ 1 \end{pmatrix}}, \boldsymbol{X} = \boldsymbol{\begin{pmatrix} \hat{\boldsymbol{x}}_1^T \\ \hat{\boldsymbol{x}}_2^T \\ \vdots \\ \hat{\boldsymbol{x}}_m^T \end{pmatrix}} X= x11x21⋮xm1x12x22⋮xm2......⋱...x1dx2d⋮xmd11⋮1 = x1Tx2T⋮xmT11⋮1 ,x^i=(xi;1)= xi1xi2⋮xid1 ,X= x^1Tx^2T⋮x^mT
现实任务中往往 X T X \boldsymbol{X^TX} XTX不是满秩矩阵。此时 w ^ \boldsymbol{\hat w} w^会有多个解,带入不同的 w ^ \boldsymbol{\hat w} w^会得到多个最小均方误差,选择哪一个将有归纳偏好决定,常见的做法是引入正则化。
到这里先解释一下,为什么 E w ^ \boldsymbol{E_{\hat w}} Ew^没有闭式解的情况下,其多个解 w ^ \boldsymbol{\hat w} w^都能使均方误差最小呢?拿如果都能最小,随便取一个 w ^ \boldsymbol{\hat w} w^当最优解的参数不就好了?
...无闭式解的情况
X T X w ^ = X T y \boldsymbol{X^TX{\hat w}=X^Ty} XTXw^=XTy
此时方程有无穷多个解。那么此时就要算通解。而非满秩矩阵的通解=特解+齐次(基础解系)通解。而通解代入方程都成立,这个方程的解是 ( E w ^ ) ′ = 0 \boldsymbol{(E_{\hat w})'=0} (Ew^)′=0的解,是极小值点,所以任意一个解都是最小均方误差 。此时要根据归纳偏好选择哪个对解决问题来说是更好的解,有更好的泛化能力。说到这,对有闭式解的情况有了提醒,哪怕是有闭式解,也不能保证模型泛化能力强,因为闭式解是在"训练阶段"最优,不是实际上的最优。
那么此时选哪个使均方误差最小从而使模型泛化能力更好那?引入正则化!
别找了,正则化在第六章,这是第三章。
.广义线性模型
\;\;\;\;\;\;\;\; 为了满足任务中输入空间到输出空间的非线性函数映射,引入广义线性模型。
定义 :对于单调可微的函数 g ( ⋅ ) \boldsymbol{g(\cdot)} g(⋅),令 y = g − 1 ( w T x + b ) \boldsymbol{y=g^{-1}(w^Tx+b)} y=g−1(wTx+b)
这样得到的模型叫做广义线性模型,其中函数 g ( ⋅ ) \boldsymbol{g(\cdot)} g(⋅)叫做联系函数。
...对数线性回归模型
\;\;\;\;\;\;\;\; 当 g ( ⋅ ) = l n ( ⋅ ) \boldsymbol{g(\cdot)=ln(\cdot)} g(⋅)=ln(⋅)的时候,叫做对数线性模型。即 y = e w T x + b \boldsymbol{y=e^{w^Tx+b}} y=ewTx+b
l n y = w T x + b \boldsymbol{lny=w^Tx+b} lny=wTx+b
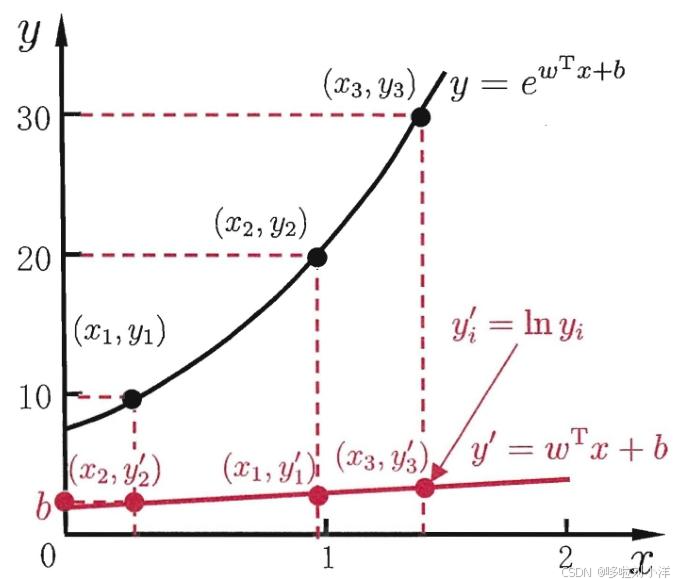
本质上仍然是线性回归,只是输出非线性。原始输出和非线性输出关系由联系函数 g ( ⋅ ) \boldsymbol{g(\cdot)} g(⋅)决定。
...对数几率回归
定义: 对数几率回归是二分类学习方法,虽名称含 "回归",实则通过线性模型逼近 "对数几率",实现对分类概率的建模。
二分类任务中,输出标记 y ∈ { 0 , 1 } \boldsymbol{y∈\{0,1\}} y∈{0,1},但线性回归的预测结果 z = w T x + b \boldsymbol{z=w^Tx+b} z=wTx+b 是实值(范围 ( − ∞ , + ∞ ) \boldsymbol{(−∞,+∞)} (−∞,+∞)),需将实值 z \boldsymbol{z} z 转换为 0/1 值。
- 单位跃迁函数
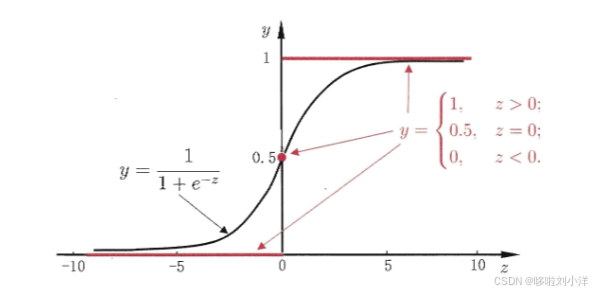
y = { 0 , z < 0 ; 0.5 , z = 0 ; 1 , z > 0 \boldsymbol{y=\begin{cases} 0, & z < 0 ; \\ 0.5, & z = 0 ; \\ 1, & z > 0 \end{cases}} y=⎩ ⎨ ⎧0,0.5,1,z<0;z=0;z>0
z > 0 \boldsymbol{z>0} z>0为正例, z < 0 \boldsymbol{z<0} z<0为反例, z = 0 \boldsymbol{z=0} z=0不确定。但是函数不连续,无法求导,无法用于基于梯度的参数优化,因此不能直接作为 "联系函数"。 - 对数几率函数(SIgmoid函数)
y = 1 1 + e − z = 1 1 + e − ( w T x + b ) ( 1 ) \boldsymbol{y=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-{(w^Tx+b)}}}} \;\;\;\;\;(1) y=1+e−z1=1+e−(wTx+b)1(1)
单调可微,输出范围严格落在 (0,1) 之间,可直接解释为 "正例概率";
对(1)进行变形:
y = 1 1 + e − ( w T x + b ) , ln y 1 − y = w T x + b y=\frac{1}{1+e^{-{(w^Tx+b)}}},\ln\frac{y}{1-y}=w^Tx+b y=1+e−(wTx+b)1,ln1−yy=wTx+b
将y视为样本x为正例的可能性,1-y为样本为反例的可能性,则称两者的比值为"几率":
y 1 − y \frac{y}{1-y} 1−yy
对齐取对数为"对数几率":
ln y 1 − y \ln\frac{y}{1-y} ln1−yy
这里就会神奇的发现, w T x + b w^Tx+b wTx+b的输出从一个无序的值变成了一个"几率"。而这个结果就是"非线性建模"得到的。将输出映射到" ln y 1 − y \ln\frac{y}{1-y} ln1−yy"
用专业术语:用线性回归模型的预测结果去逼近真实标记的对数几率,因此,其对应的模型称为"对数几率回归" 。
.求解对数几率参数
\;\;\;\;\;\;\;\; 知道了什么是对数几率模型,现在就是求解它的参数。
ln y 1 − y = w T x + b \ln\frac{y}{1-y}=w^Tx+b ln1−yy=wTx+b
将 y y y视为类后验概率估计 p ( y = 1 ∣ x ) p(y = 1 |x) p(y=1∣x),简单说就算知道x的前提下,得到y=1的概率是多少。
ln p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) = w T x + b \ln \frac{p(y=1|\boldsymbol{x})}{p(y=0|\boldsymbol{x})} = \boldsymbol{w}^T \boldsymbol{x} + b lnp(y=0∣x)p(y=1∣x)=wTx+b
从而得到:
p ( y = 1 ∣ x ) = e w T x + b 1 + e w T x + b ( 1 ) p(y=1|\boldsymbol{x}) = \frac{e^{\boldsymbol{w}^T \boldsymbol{x} + b}}{1 + e^{\boldsymbol{w}^T \boldsymbol{x} + b}}\;\;\;\;(1) p(y=1∣x)=1+ewTx+bewTx+b(1)
p ( y = 0 ∣ x ) = 1 1 + e w T x + b ( 2 ) p(y=0|\boldsymbol{x}) = \frac{1}{1 + e^{\boldsymbol{w}^T \boldsymbol{x} + b}}\;\;\;\;(2) p(y=0∣x)=1+ewTx+b1(2)
我们通过"极大似然法"来估计w和b,给定数据集 { ( x i , y i ) } i m \{(x_i,y_i)\}i^m {(xi,yi)}im,对率回归模型最大化"对数似然"。
ℓ ( w , b ) = ∑ i = 1 m ln p ( y i ∣ x i ; w , b ) ( 3 ) \ell(\boldsymbol{w}, b) = \sum{i=1}^m \ln p(y_i | \boldsymbol{x}_i; \boldsymbol{w}, b) (3) ℓ(w,b)=i=1∑mlnp(yi∣xi;w,b)(3)
即令每个样本属于其真实标记的概率越大越好。
为便于讨论,令 β = ( w ; b ) β=(w;b) β=(w;b), x ^ = ( x ; 1 ) {\hat x}=(x;1) x^=(x;1), 则 w T x + b w^Tx+b wTx+b 可简写为 β T x ^ β^T{\hat x} βTx^, 再令 p 1 ( x ^ ; β ) = p ( y = 1 ∣ x ^ ; β ) p_1(\hat x;β)=p(y=1∣\hat x;β) p1(x^;β)=p(y=1∣x^;β), p 0 ( x ^ ; β ) = p ( y = 0 ∣ x ^ ; β ) = 1 − p 1 ( x ^ ; β ) p_0(\hat x;β)=p(y=0∣\hat x;β)=1−p_1(\hat x;β) p0(x^;β)=p(y=0∣x^;β)=1−p1(x^;β), 则式 (3) 中的似然项可重写为:
p ( y i ∣ x i ; w , b ) = y i p 1 ( x ^ i ; β ) + ( 1 − y i ) p 0 ( x ^ i ; β ) ( 4 ) p(y_i∣x_i;w,b)=y_ip_1(\hat x_i;β)+(1−y_i)p_0(\hat x _i;β) \;\;\;\;(4) p(yi∣xi;w,b)=yip1(x^i;β)+(1−yi)p0(x^i;β)(4)
将式 (4) 代入 (3),结合(1)(2)最大化式 (3) 等价于最小化
ℓ ( β ) = ∑ i = 1 m ( − y i β T x ^ i + l n ( 1 + e β T x i ) ) ( 5 ) ℓ(β)=\sum_{i=1}^m(−y_iβ^T\hat x^i+ln(1+e^{β^Tx^i}))\;\;\;\;(5) ℓ(β)=i=1∑m(−yiβTx^i+ln(1+eβTxi))(5)
具体推导(5):
(4)代入(3)
ℓ ( β ) = ∑ i = 1 m ln ( y i p 1 ( x ^ i ; β ) + ( 1 − y i ) p 0 ( x ^ i ; β ) ) ( 6 ) \ell(\boldsymbol{\beta}) = \sum_{i=1}^{m} \ln \left( y_i p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) + (1 - y_i) p_0(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \right)\;\;\;(6) ℓ(β)=i=1∑mln(yip1(x^i;β)+(1−yi)p0(x^i;β))(6)
由(1),(2)得 p 1 ( x ^ i ; β ) = e β T x ^ i 1 + e β T x ^ i , p 0 ( x ^ i ; β ) = 1 1 + e β T x ^ i p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) = \frac{\mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}}{1+\mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}}, \quad p_0(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) = \frac{1}{1+\mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}} p1(x^i;β)=1+eβTx^ieβTx^i,p0(x^i;β)=1+eβTx^i1 代入(6)得:
ℓ ( β ) = ∑ i = 1 m ln ( y i e β T x ^ i + 1 − y i 1 + e β T x ^ i ) = ∑ i = 1 m ( ln ( y i e β T x ^ i + 1 − y i ) − ln ( 1 + e β T x ^ i ) ) \ell(\boldsymbol{\beta}) = \sum_{i=1}^{m} \ln \left( \frac{y_i \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i} + 1 - y_i}{1 + \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}i}} \right)= \sum{i=1}^{m} \left( \ln(y_i \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i} + 1 - y_i) - \ln(1 + \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}) \right) ℓ(β)=i=1∑mln(1+eβTx^iyieβTx^i+1−yi)=i=1∑m(ln(yieβTx^i+1−yi)−ln(1+eβTx^i))
由于 y i = 0 或 1 y_i=0或1 yi=0或1,因此
ℓ ( β ) = { ∑ i = 1 m ( − ln ( 1 + e β T x ^ i ) ) , y i = 0 ∑ i = 1 m ( β T x ^ i − ln ( 1 + e β T x ^ i ) ) , y i = 1 \ell(\boldsymbol{\beta}) = \begin{cases} \displaystyle\sum_{i=1}^{m} \left( -\ln(1 + \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}i}) \right), & y_i = 0 \\ \displaystyle\sum{i=1}^{m} \left( \boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i - \ln(1 + \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}) \right), & y_i = 1 \end{cases} ℓ(β)=⎩ ⎨ ⎧i=1∑m(−ln(1+eβTx^i)),i=1∑m(βTx^i−ln(1+eβTx^i)),yi=0yi=1
将两式综合可得
ℓ ( β ) = ∑ i = 1 m ( y i β T x ^ i − ln ( 1 + e β T x ^ i ) ) ( 7 ) \ell(\boldsymbol{\beta}) = \sum_{i=1}^{m} \left( y_i \boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i - \ln(1 + \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}) \right)\;\;\;\;(7) ℓ(β)=i=1∑m(yiβTx^i−ln(1+eβTx^i))(7)
另一种推导方式
将式 (4) 改写为 p ( y i ∣ x i ; w , b ) = [ p 1 ( x ^ i ; β ) ] y i [ p 0 ( x ^ i ; β ) ] 1 − y i p(y_i|x_i; \boldsymbol{w}, b) = [p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta})]^{y_i} [p_0(\hat{\boldsymbol{x}}i; \boldsymbol{\beta})]^{1-y_i} p(yi∣xi;w,b)=[p1(x^i;β)]yi[p0(x^i;β)]1−yi,代入式 (3) 可得
ℓ ( β ) = ∑ i = 1 m ln ( [ p 1 ( x ^ i ; β ) ] y i [ p 0 ( x ^ i ; β ) ] 1 − y i ) = ∑ i = 1 m [ y i ln ( p 1 ( x ^ i ; β ) ) + ( 1 − y i ) ln ( p 0 ( x ^ i ; β ) ) ] = ∑ i = 1 m { y i [ ln ( p 1 ( x ^ i ; β ) ) − ln ( p 0 ( x ^ i ; β ) ) ] + ln ( p 0 ( x ^ i ; β ) ) } = ∑ i = 1 m [ y i ln ( p 1 ( x ^ i ; β ) p 0 ( x ^ i ; β ) ) + ln ( p 0 ( x ^ i ; β ) ) ] = ∑ i = 1 m [ y i ln ( e β T x ^ i ) + ln ( 1 1 + e β T x ^ i ) ] = ∑ i = 1 m ( y i β T x ^ i − ln ( 1 + e β T x ^ i ) ) \begin{aligned} \ell(\boldsymbol{\beta}) &= \sum{i=1}^{m} \ln \left( [p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta})]^{y_i} [p_0(\hat{\boldsymbol{x}}i; \boldsymbol{\beta})]^{1-y_i} \right) \\ &= \sum{i=1}^{m} \left[ y_i \ln \left( p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \right) + (1 - y_i) \ln \left( p_0(\hat{\boldsymbol{x}}i; \boldsymbol{\beta}) \right) \right] \\ &= \sum{i=1}^{m} \left\{ y_i \left[ \ln \left( p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \right) - \ln \left( p_0(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \right) \right] + \ln \left( p_0(\hat{\boldsymbol{x}}i; \boldsymbol{\beta}) \right) \right\} \\ &= \sum{i=1}^{m} \left[ y_i \ln \left( \frac{p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta})}{p_0(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta})} \right) + \ln \left( p_0(\hat{\boldsymbol{x}}i; \boldsymbol{\beta}) \right) \right] \\ &= \sum{i=1}^{m} \left[ y_i \ln \left( \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i} \right) + \ln \left( \frac{1}{1+\mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}i}} \right) \right] \\ &= \sum{i=1}^{m} \left( y_i \boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i - \ln(1 + \mathrm{e}^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}) \right) \end{aligned} ℓ(β)=i=1∑mln([p1(x^i;β)]yi[p0(x^i;β)]1−yi)=i=1∑m[yiln(p1(x^i;β))+(1−yi)ln(p0(x^i;β))]=i=1∑m{yi[ln(p1(x^i;β))−ln(p0(x^i;β))]+ln(p0(x^i;β))}=i=1∑m[yiln(p0(x^i;β)p1(x^i;β))+ln(p0(x^i;β))]=i=1∑m[yiln(eβTx^i)+ln(1+eβTx^i1)]=i=1∑m(yiβTx^i−ln(1+eβTx^i))
式 (7) 是关于 β 的高阶可导连续凸函数,根据凸优化理论,经典的数值优化算法如梯度下降法 、牛顿法等都可求得其最优解,于是就得到
β ∗ = arg min β ℓ ( β ) \boldsymbol{\beta}^* = \arg\min_{\boldsymbol{\beta}} \ell(\boldsymbol{\beta}) β∗=argβminℓ(β)
以牛顿法为例,其第 t + 1 轮选代解的更新公式为
β t + 1 = β t − ( ∂ 2 ℓ ( β ) ∂ β ∂ β T ) − 1 ∂ ℓ ( β ) ∂ β \boldsymbol{\beta}^{t+1} = \boldsymbol{\beta}^t - \left( \frac{\partial^2 \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\mathrm{T}}} \right)^{-1} \frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} βt+1=βt−(∂β∂βT∂2ℓ(β))−1∂β∂ℓ(β)
其中关于 β 的 一 阶、 二 阶导数分别为
∂ ℓ ( β ) ∂ β = − ∑ i = 1 m x ^ i ( y i − p 1 ( x ^ i ; β ) ) \frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = -\sum_{i=1}^{m} \hat{\boldsymbol{x}}_i \left( y_i - p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \right) ∂β∂ℓ(β)=−i=1∑mx^i(yi−p1(x^i;β))
∂ 2 ℓ ( β ) ∂ β ∂ β T = ∑ i = 1 m x ^ i x ^ i T p 1 ( x ^ i ; β ) ( 1 − p 1 ( x ^ i ; β ) ) \frac{\partial^2 \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\mathrm{T}}} = \sum_{i=1}^{m} \hat{\boldsymbol{x}}_i \hat{\boldsymbol{x}}_i^{\mathrm{T}} p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \left( 1 - p_1(\hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) \right) ∂β∂βT∂2ℓ(β)=i=1∑mx^ix^iTp1(x^i;β)(1−p1(x^i;β))
关于牛顿法,梯度下降法将单独开一个文章详细讲解。