PT²-LLM:面向大型语言模型的训练后三元量化
作者:¹ 上海交通大学、² 苏黎世联邦理工学院、³ 腾讯混元*
(与ARB-LLM: Alternating Refined Binarizations for Large Language Models的作者有重叠)
摘要
大型语言模型(LLMs)在各类任务中展现出令人瞩目的能力,但庞大的内存占用和计算需求阻碍了其部署。三元量化作为一种极具潜力的压缩技术,能够大幅降低模型尺寸并提升计算效率,因而受到广泛关注。然而,由于无训练参数优化的挑战,以及异常值和分散权重带来的量化难题,其在训练后量化(PTQ)场景中的潜力尚未得到充分挖掘。为解决这些问题,我们提出 PT²-LLM,一种专为大型语言模型设计的训练后三元量化框架。该框架的核心是一个非对称三元量化器,配备两阶段精炼流水线:(1)迭代三元拟合(ITF),通过交替进行最优三元网格构建和灵活舍入,最小化量化误差;(2)激活感知网格对齐(AGA),进一步精炼三元网格,以更好地匹配全精度输出。此外,我们提出一种即插即用的基于结构相似性的重排序(SSR)策略,利用列间结构相似性简化量化过程并减轻异常值影响,从而进一步提升整体性能。大量实验表明,PT²-LLM 在内存成本更低的情况下,与最先进的(SOTA)2 位训练后量化方法相比表现出竞争力,同时加速预填充和解码过程,实现端到端提速。代码和模型将在https://github.com/XIANGLONGYAN/PT2-LLM 公开。
1 引言
大型语言模型(LLMs)(Touvron 等人,2023a;b;Dubey 等人,2024;Yang 等人,2025;Zhang 等人,2022)在语言理解、推理和生成方面取得了显著进展。它们是众多实际应用的基础,始终处于人工智能研究的前沿。然而,这些成就很大程度上依赖于模型参数的庞大规模。现代大型语言模型通常包含数百亿甚至数千亿个参数(例如,DeepSeek-R1(Guo 等人,2025)拥有 6710 亿个参数),导致巨大的内存消耗和密集的计算需求。运行此类模型需要强大的图形处理器(GPU)、大容量内存和高能耗,这阻碍了其在资源受限或延迟敏感的平台上部署。
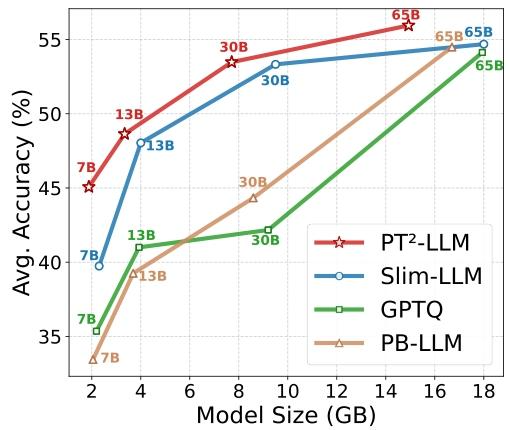
图 1:LLaMA模型在 7 个零样本问答(QA)数据集上的性能。在相同内存成本下,PT²-LLM 实现了最佳准确率。
仅权重量化(Frantar 等人,2023)通过降低权重精度来节省内存并加速推理。在各种方案中,三元量化(Li 等人,2016)将权重限制在 {−1, 0, +1} 集合中,能够实现高压缩比和高效计算。与低位量化(例如 2-4 位)(Lin 等人,2024b)相比,它通过使用简单的加法替代大部分浮点乘法,同时降低计算成本和能耗。与二值化(Rastegari 等人,2016)相比,三元量化更适合大型语言模型权重的单峰分布,并且具有更强的表示能力,能够获得更高的准确率。三元量化在效率和表达性之间取得了平衡,适用于资源受限场景下的大型语言模型部署(Wang 等人,2025;Yin 等人,2025)。
近期关于三元量化的研究(Lu 等人,2024;Zhang 等人,2020)主要集中在量化感知训练(QAT),即模型在三元约束下进行训练。此类方法主要在中等规模的架构(如 BERT 或 DiT)上进行探索,这些架构的训练成本相对可控。尽管已有尝试将基于量化感知训练的三元量化扩展到大型语言模型(例如 BitNet b1.58(Ma 等人,2024)),但由于参数规模庞大,且对训练资源、计算预算和完整训练数据的需求极高,这些方法在实际应用中并不可行。相比之下,训练后量化(PTQ)提供了一种更为实用高效的替代方案:它无需重新训练或获取完整训练数据,就能快速将全精度模型转换为紧凑的三元版本,更适合实际的大型语言模型部署场景。
然而,基于训练后量化的三元量化研究仍不够充分,直接应用往往会导致模型性能严重下降,使其无法使用。通过分析,我们发现两个主要挑战:(i)与量化感知训练不同,量化感知训练通过在大规模训练数据上进行基于梯度的更新来优化三元参数,而训练后量化必须在无任何训练的情况下高效精炼这些参数,这是一个核心挑战;(ii)作为一种极端的低位量化方案,三元量化难以表示具有分散分布或富含异常值的权重,因此特别容易产生较大的量化误差。
在本文中,我们提出 PT²-LLM,一种专为大型语言模型设计的训练后三元量化框架。为应对无训练三元参数优化的挑战,我们提出非对称三元量化器(ATQ),通过两个阶段进行精炼:迭代三元拟合(ITF)和激活感知网格对齐(AGA)。迭代三元拟合交替进行最优三元网格构建和灵活舍入,以最小化量化误差;而激活感知网格对齐利用校准数据,进一步使三元输出与全精度输出对齐。为处理分散权重和异常值,我们提出即插即用的基于结构相似性的重排序(SSR)策略,该策略基于列间结构相关性重新组织列,以简化量化过程。配备非对称三元量化器和基于结构相似性的重排序后,PT²-LLM 能够实现准确且稳健的训练后三元量化。如图 1 所示,在相同内存预算下,它在零样本问答准确率方面优于最先进的 2 位训练后量化方法。
我们的主要贡献总结如下:
- 提出 PT²-LLM,一种新颖的三元量化框架,能够在无需任何重新训练的情况下,将预训练大型语言模型高效压缩为三元网格,解决了大型语言模型训练后三元量化中尚未被探索的挑战。
- 设计用于训练后三元量化的非对称三元量化器。它通过两个无训练阶段进行优化:迭代三元拟合(ITF)和激活感知网格对齐(AGA)。这些组件能够有效精炼三元参数,减少量化误差,并提高与全精度输出的对齐度。
- 提出即插即用的基于结构相似性的重排序(SSR)策略。该策略基于结构相似性对权重列进行重排序,有助于降低量化难度并抑制异常值的影响。
大量实验表明,与最先进的 2 位训练后量化方法相比,PT²-LLM 具有竞争力的性能,同时降低了内存消耗并加快了推理速度。
2 相关工作
2.1 网络三元量化
三元量化通过将参数约束在 {−1, 0, +1} 集合中来压缩神经网络,在保持强大表示能力的同时,实现内存高效和计算高效。三元权重网络(TWN)(Li 等人,2016)引入了尺度感知三元量化,以最小化与全精度的欧几里得距离,实现了高达 16 倍的压缩比。训练三元量化(TTQ)(Zhu 等人,2016)通过在训练过程中联合学习三元权重值及其分配,提高了准确率。后续研究(Wang 等人,2018;Alemdar 等人,2017)将三元量化扩展到激活值,实现了效率更高的全三元网络。近年来,研究人员致力于将三元量化应用于更大、更复杂的模型。三元 BERT(TernaryBERT)(Zhang 等人,2020)通过损失感知三元量化和蒸馏,实现了 14.9 倍的 BERT 压缩。三元扩散转换器(TerDiT)(Lu 等人,2024)将三元量化扩展到 420 亿参数的扩散转换器。三元大型语言模型(TernaryLLM)(Chen 等人,2024)引入了可学习缩放和特征蒸馏,性能优于先前的低位大型语言模型。BitNet b1.58(Ma 等人,2024)提出了用于大型语言模型的三元权重训练框架,在降低延迟和能耗的同时,实现了接近全精度的准确率。然而,大多数现有三元量化方法依赖于训练,限制了其在实际部署中的实用性。
2.2 大型语言模型的量化
量化能够减少大型语言模型的内存占用和推理成本,通常分为量化感知训练(QAT)和训练后量化(PTQ)两类。
- 量化感知训练(QAT):量化感知训练在训练过程中融入量化操作,使大型语言模型能够通过反向传播学习稳健的低位表示。诸如 LLM-QAT(Liu 等人,2024a)和 BitDistiller(Du 等人,2024)等工作利用知识蒸馏,在低位量化下保持准确率。高效量化感知训练(EfficientQAT)(Chen 等人,2025)通过两阶段训练方案降低了量化感知训练的开销。近期研究(如 Onebit(Xu 等人,2024)和 BinaryMoS(Jo 等人,2024))进一步将量化感知训练扩展到一位量化领域。尽管量化感知训练能够在低位量化下有效保持性能,但高昂的计算和内存成本仍然是其主要限制。
- 训练后量化(PTQ):与量化感知训练不同,训练后量化直接对预训练模型进行量化,无需重新训练,因此对于大型语言模型而言更高效且易于部署。早期方法(Dettmers 等人,2022;Yao 等人,2022;Li 等人,2021)通过引入分组标签来改进量化效果。诸如激活感知权重量化(AWQ)(Lin 等人,2024b)和异常值感知权重量化(OWQ)(Lee 等人,2024)等技术引入了对显著权重的缩放变换,旨在保留激活表达性和整体模型容量。生成式预训练变压器量化(GPTQ)(Frantar 等人,2023)利用黑塞矩阵引导的误差补偿,而生成式预训练变压器不对称量化(GPTAQ)(Li 等人,2025a)通过不对称校准对其进行了扩展。全量化(OmniQuant)(Shao 等人,2023)和平滑量化(SmoothQuant)(Xiao 等人,2023)通过尺度重分配来处理激活异常值。近期研究(Lin 等人,2024a;Ashkboos 等人,2024;Liu 等人,2024b)采用基于旋转的变换来改进低位量化效果。在超低位设置下,量化与不连贯处理(QuIP)(Chee 等人,2025)和增强型量化与不连贯处理(QuIP#)(Tseng 等人,2025)利用不连贯处理来提升性能,而精简大型语言模型(Slim-LLM)(Huang 等人,2025)采用显著性驱动的混合精度方案。在二值化领域,一位方法(如部分二值化大型语言模型(PB-LLM)(Shang 等人,2024)、二元大型语言模型(BiLLM)(Huang 等人,2024)和交替精炼二值化大型语言模型(ARB-LLM)(Li 等人,2025b))展现出具有竞争力的结果。亚一位方法(Dong 等人,2025;Yan 等人,2025;Gu 等人,2025)通过降低平均位宽进一步推进了压缩技术,同时保持了较强的准确率。我们的方法属于训练后三元量化类别。
3 方法
概述:图 2 展示了 PT²-LLM 的整体工作流程。我们首先在 3.1 节中回顾标准对称三元量化公式和基本符号。在此基础上,3.2 节介绍非对称三元量化器,该量化器具有两个无训练阶段:迭代三元拟合(ITF)和激活感知网格对齐(AGA)。3.3 节随后介绍基于结构相似性的重排序(SSR),展示如何将基于结构相似性的列聚类有效整合到生成式预训练变压器量化(GPTQ)框架中。
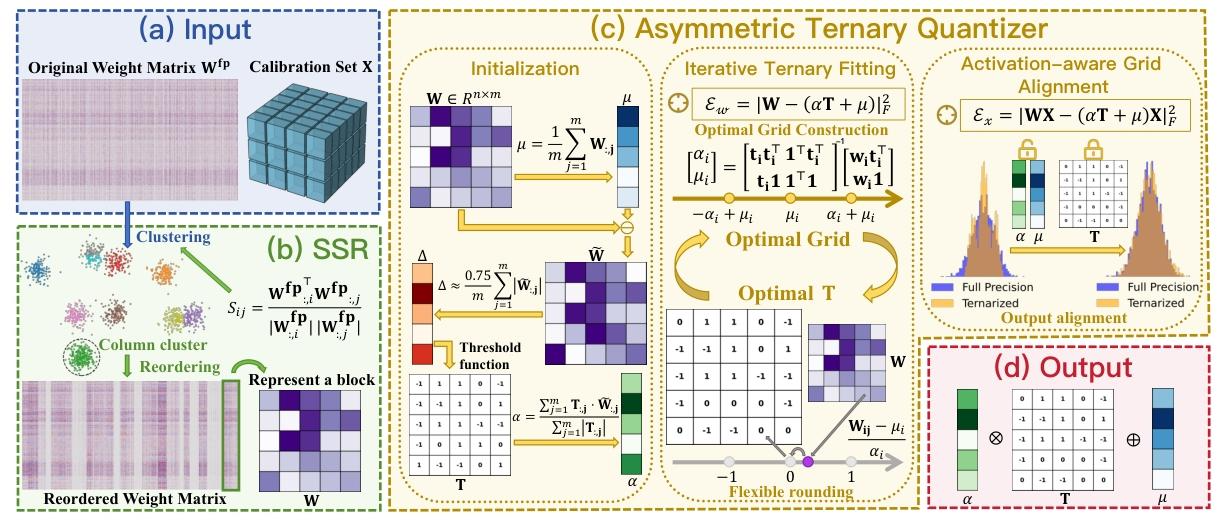
图 2:PT²-LLM 的概述。基于结构相似性的重排序(SSR) :基于结构相似性对列 进行重排序 。非对称三元量化器 :通过迭代三元拟合(ITF)和激活感知网格对齐(AGA)增强,用于精炼三元参数优化。
3.1 预备知识
对称三元量化:对称三元量化通过适当的缩放,将全精度权重压缩到三元集合{−1, 0, +1}中,以最小化原始权重矩阵与其三元近似之间的差异:
\( \alpha^*, T^* = \arg\min_{\alpha, T} \| W - \alpha T \|F^2 \) (1)
其中,\( W \in \mathbb{R}^{n \times m} \) 是全精度权重矩阵,\( \alpha \in \mathbb{R}^{n \times 1} \) 是行方向缩放因子,\( T \in \{-1, 0, +1\}^{n \times m} \) 是三元矩阵。由于联合优化\( \alpha \)和\( T \)会导致参数耦合,三元权重网络(TWN)(Li等人,2016)提出了一种基于阈值的解决方案。具体而言,对于每个元素\( w{ij} \),使用行方向阈值\( \Delta_i \)来确定相应的三元值\( T_{ij} \):
\( T_{ij} = \begin{cases}
1, & \text{若 } W_{ij} > \Delta_i, \\
0, & \text{若 } |W_{ij}| \leq \Delta_i, \\
-1, & \text{若 } W_{ij} < -\Delta_i.
\end{cases} \) (2)
给定固定阈值\( \Delta \),三元矩阵\( T \)被确定性定义,从而可以获得最优缩放因子\( \alpha \)的闭式解。由于在实际中直接优化\( \Delta \)较为困难,三元权重网络(TWN)基于假设的权重分布来近似\( \Delta \)。假设权重服从均匀或正态先验,\( \Delta \)通过绝对权重的缩放均值来近似,而最优\( \alpha \)如下:
\( \Delta \approx \frac{0.75}{m} \sum_{j=1}^m |W_{:,j}|, \quad \alpha = \frac{\sum_{j=1}^m T_{:,j} \cdot W_{:,j}}{\sum_{j=1}^m |T_{:,j}|} \)
这种近似通过解耦\( \alpha \)和\( T \),实现了快速且无训练的三元量化,为训练后量化场景中的三元参数初始化提供了实用解决方案。
3.2 非对称三元量化器
非对称三元初始化:实证观察表明,大型语言模型中的权重分布并不总是对称的,许多层表现出非零均值。我们在补充材料中提供了可视化结果以进一步支持这一观察。尽管对称三元量化(如3.1节所述)在量化感知训练下表现良好,因为它能够通过反向传播重塑权重分布,但在训练后量化场景中,预训练权重保持固定,这一假设不再成立。为了更好地捕捉预训练权重中的偏差,我们借鉴先前的工作(Chen等人,2024),采用非对称三元量化方案,引入行方向偏移\( \mu \in \mathbb{R}^{n \times 1} \),其初始化为每行的均值。反量化权重\( \hat{W} \)计算如下:
\( \hat{W} = \alpha T + \mu, \quad \mu = \frac{1}{m} \sum_{j=1}^m W_{:,j} \)
对于\( \alpha \)和三元矩阵\( T \)的初始化,我们遵循3.1节中描述的相同策略,将其应用于中心化权重矩阵\( \tilde{W} = W - \mu \)以去除偏差:
\( \Delta \approx \frac{0.75}{m} \sum_{j=1}^m |\tilde{W}{:,j}|, \quad \alpha = \frac{\sum{j=1}^m T_{:,j} \cdot \tilde{W}{:,j}}{\sum{j=1}^m |T_{:,j}|} \)
\( T \)仍使用公式(2)进行初始化,其中\( \Delta \)应用于\( \tilde{W} \)。这种非对称初始化在非零均值权重分布下,为训练后三元量化提供了稳定且具有表达力的基础。
迭代三元拟合:初始化后,我们获得三元量化的三个关键组件:缩放因子\( \alpha \)、偏移参数\( \mu \)和三元矩阵\( T \)。\( \alpha \)和\( \mu \)共同定义了一个三元网格,每行仅有三个可能的量化值,即\( \{-\alpha_i + \mu_i, \mu_i, \alpha_i + \mu_i\} \)。如何精炼这个三元网格以更好地适应底层权重分布,对于提高量化质量至关重要。我们首先定义权重量化误差\( \mathcal{E}_w \):
\( \mathcal{E}_w = \| W - \hat{W} \|_F^2, \quad \text{其中 } \hat{W} = \alpha T + \mu \) (6)
我们当前的优化目标是最小化量化误差\( \mathcal{E}_w \),这通过优化三元量化参数\( \alpha \)、\( \mu \)和\( T \)来实现。由于\( \alpha \)和\( \mu \)共同决定了三元量化的离散网格值,我们将它们称为三元网格参数。构建高质量的网格是后续优化三元矩阵\( T \)的可靠基础。因此,我们首先专注于建立高质量的三元网格。通过对量化误差\( \mathcal{E}w \)关于\( \alpha_i \)和\( \mu_i \)求导,我们得到以下梯度:
\( \frac{\partial \mathcal{E}w}{\partial \alpha_i} = 2 \left( \alpha_i t_i + \mu_i 1^\top - w_i \right) t_i^\top, \quad \frac{\partial \mathcal{E}w}{\partial \mu_i} = 2 \left( \alpha_i t_i + \mu_i 1^\top - w_i \right) 1 \)
其中,\( t_i \in \mathbb{R}^{1 \times m} \)表示\( T \)的第\( i \)行,\( w_i \in \mathbb{R}^{1 \times m} \)是\( W \)对应的行,\( 1 \in \mathbb{R}^{m \times 1} \)是全1列向量。参数\( \alpha_i \)和\( \mu_i \)分别是与第\( i \)行相关联的缩放因子和偏移量。为了获得最优三元网格参数,我们令偏导数为零并求解\( \alpha_i \)和\( \mu_i \)。这导致了一个关于最优网格参数\( \alpha_i \)和\( \mu_i \)的线性方程组(详细推导见补充材料):
\( \frac{\partial \mathcal{E}w}{\partial \alpha_i} = 0, \frac{\partial \mathcal{E}w}{\partial \mu_i} = 0 \implies \begin{bmatrix} t_i t_i^\top & 1^\top t_i^\top \\ t_i 1 & 1^\top 1 \end{bmatrix} \begin{bmatrix} \alpha_i \\ \mu_i \end{bmatrix} = \begin{bmatrix} w_i t_i^\top \\ w_i 1 \end{bmatrix} \) (8)
该方程组可以高效求解,以获得第\( i \)行的最优三元网格。为了实现跨多行的高效批量计算,我们进一步将\( \alpha^* \)和\( \mu^* \)的最优解重新表述为更紧凑的向量化形式(详细推导见补充材料):
\( \alpha^* = \frac{m \cdot (W \circ T) 1 - (T 1) \circ (W 1)}{m \cdot (T \circ T) 1 - (T 1)^2}, \quad \mu^* = \frac{(T \circ T) 1 \circ (W 1) - (T 1) \circ [(W \circ T) 1]}{m \cdot (T \circ T) 1 - (T 1)^2} \) (9)
其中,\( \circ \)表示按元素乘法,所有除法也为按元素除法,\( m \)是每行的元素数量。这种向量化形式支持跨多行的并行闭式求解,确保在固定\( T \)下获得最优\( \alpha^* \)和\( \mu^* \),从而得到当前阶段的最佳三元网格。获得当前最优三元网格后,我们通过将全精度权重映射到该网格上来更新\( T \)。与固定阈值(其具有刚性,且对于多样的权重分布通常不是最优的)不同,我们采用更灵活的按元素三元舍入,以最小化量化误差\( \mathcal{E}w \)(公式(6))。给定\( \alpha^* \)和\( \mu^* \),每个元素\( T{ij}^* \)的最优值由以下规则确定:
\( T{ij}^* = \arg\min{t \in \{-1, 0, +1\}} | Z{ij} - t |, \quad \text{其中 } Z{ij} = \frac{W{ij} - \mu_i^*}{\alpha_i^*} \) (10)
这保证了在固定\( \alpha^* \)和\( \mu^* \)的情况下,更新后的\( T^* \)能够产生最小的量化误差\( \mathcal{E}_w \),使其成为当前网格的最优三元分配。我们观察到,获得最优三元网格和最优三元矩阵自然形成了一种迭代优化方案。通过交替执行公式(9)和公式(10),该算法在每一步贪婪地降低量化误差\( \mathcal{E}_w \)。当公式(10)中的更新不再改变三元矩阵\( T \)时,表明三元化结构已稳定,此时达到收敛。在实际应用中,该算法大约在10次迭代内收敛。
激活感知网格对齐:尽管迭代三元拟合有效地最小化了权重量化误差\( \mathcal{E}_w \),但大型语言模型的实际输出取决于权重和激活之间的相互作用。为解决这一问题,我们引入激活感知输出误差\( \mathcal{E}_x \):
\( \mathcal{E}_x = \| W X - \hat{W} X \|_F^2, \quad \text{其中 } \hat{W} = \alpha T + \mu \) (11)
算法1:非对称三元量化器的伪代码。详细信息见补充材料。
```
func ATQ(W, X)
输入:W ∈ R^(n×m) - 权重矩阵;X ∈ R^(B×L×m) - 校准数据
输出:W_quant ∈ R^(n×m) - 量化后的权重矩阵
1: α, µ, T := 三元初始化(W)
2: T_prev := 0
3: while T ≠ T_prev do
4: T_prev ← T
5: α, µ ← 构建最优网格(T, W)
6: T ← 灵活舍入(W, α, µ)
7: end while
8: α, µ ← 激活感知网格对齐(W, T, X)
9: W_quant ← αT + µ
10: return W_quant
```

其中,\( X \in \mathbb{R}^{B × L × m} \)表示校准数据,\( B \)为批量大小,\( L \)为序列长度,\( m \)为嵌入维度。该公式将量化与模型输出直接耦合,确保优化更能反映实际场景。与迭代三元拟合类似,我们再次对\( \mathcal{E}_x \)关于\( \alpha_i \)和\( \mu_i \)求导,令导数为零,得到在当前目标下的最优三元网格方程组。与之前一样,解按行表示为第\( i \)个组件:
\( \frac{\partial \mathcal{E}x}{\partial \alpha_i} = 0, \frac{\partial \mathcal{E}x}{\partial \mu_i} = 0 \implies \begin{bmatrix} t_i C t_i^\top & 1^\top C t_i^\top \\ t_i C 1 & 1^\top C 1 \end{bmatrix} \begin{bmatrix} \alpha_i \\ \mu_i \end{bmatrix} = \begin{bmatrix} w_i C t_i \\ w_i C 1 \end{bmatrix} \) (12)
其中,\( C = \sum_b \sum_i X{bi} X{bi}^\top \)。通过求解该方程组,我们得到闭式解:
\( \alpha^* = \frac{d \cdot (W \circ T) S 1 - v \circ (W S 1)}{d \cdot T^2 S 1 - v^2}, \quad \mu^* = \frac{T^2 S 1 \circ (W S 1) - v \circ [(W \circ T) S 1]}{d \cdot T^2 S 1 - v^2} \) (13)
其中,\( d = 1^\top S 1 \)是标量,\( v = T S 1 \),\( T^2 \)和\( v^2 \)表示按元素平方。这种激活感知的网格参数对齐显著提高了量化输出与全精度输出的一致性。理想情况下,我们可以更新\( T \)以进一步降低输出误差\( \mathcal{E}_x \),但与迭代三元拟合不同,此时不存在最优解。虽然可以进行贪婪搜索,但在实际应用中我们观察到,更新\( T \)会导致在校准集上的严重过拟合。因此,我们冻结\( T \),仅更新一次\( (\alpha, \mu) \),这已经能够得到准确的近似结果。关于过拟合的详细信息见补充材料。
非对称三元量化器整体工作流程:如算法1所示,非对称三元量化器通过迭代三元拟合精炼三元参数以获得更准确的\( T \),然后应用激活感知网格对齐进一步使三元网格参数与输出对齐,最终得到量化权重。在图3(左图和中图)中,我们绘制了各步骤的量化误差\( \mathcal{E}_w \)和输出误差\( \mathcal{E}_x \)。在迭代三元拟合过程中,\( \mathcal{E}_w \)稳步下降,而在激活感知网格对齐更新后,由于优化目标的转变,\( \mathcal{E}_w \)略有上升;\( \mathcal{E}_x \)在迭代三元拟合过程中适度下降,在激活感知网格对齐后急剧下降。总体而言,结果表明非对称三元量化器在无需重新训练的情况下,同时降低了量化误差和输出误差。
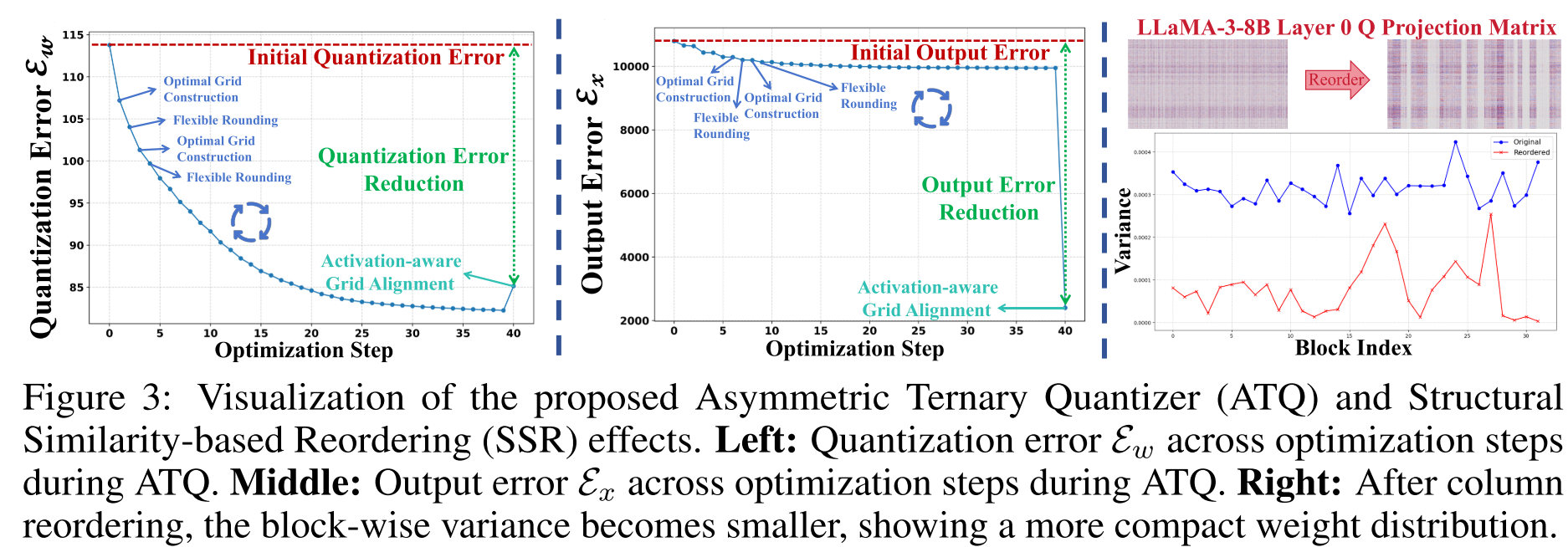
图3:所提出的非对称三元量化器(ATQ)和基于结构相似性的重排序(SSR)效果的可视化。左图:ATQ优化步骤中的量化误差\( \mathcal{E}_w \)。中图:ATQ优化步骤中的输出误差\( \mathcal{E}_x \)。右图:列重排序后,块内方差变小,显示出更紧凑的权重分布。
3.3 基于结构相似性的重排序
动机:借鉴生成式预训练变压器量化(GPTQ)(Frantar等人,2023),我们的三元量化采用块级方式:将大型权重矩阵分割为固定大小的块,并独立进行量化。尽管与一次性量化整个矩阵相比,这种方式提高了准确率,但我们发现简单的块级三元量化仍会导致严重的性能下降。为了探究原因,我们分析了权重分布并发现两个关键问题:(i)块内权重通常表现出高方差,使得三元量化过于粗糙,从而导致较大的量化误差;(ii)许多层表现出列方向偏差,异常值列会扭曲三元量化范围并降低保真度。
结构感知列聚类:为解决这些问题,我们重新审视列重排序技术,该技术在生成式预训练变压器量化(GPTQ)(Frantar等人,2023)中被作为可选技术提供:虽然生成式预训练变压器量化(GPTQ)可以按固定顺序量化权重,但已有研究表明,按黑塞矩阵推导的重要性对列进行重排序能够提高性能。形式上,重排序可以通过置换矩阵\( P \)表示:
\( W' = W P, \quad X' = X P, \quad X' W'^\top = X W^\top \) (14)
这里\( P \)仅对列进行置换,因此矩阵乘法的结果保持不变。由于应用\( P \)仅涉及索引重排序而非实际乘法运算,推理过程中的计算开销可以忽略不计。基于这一形式,我们观察到重排序的潜力尚未得到充分挖掘。将结构相似且数值接近的列放在同一个块中,能够得到更紧凑的分布,从而改进行方向三元量化效果。类似地,将异常值分组在一起可以防止它们扭曲正常列------异常值中的异常值不再是异常值。为此,我们提出一种简单而有效的结构感知列聚类方法。具体而言,我们计算权重列之间的成对余弦相似度,以捕捉它们的结构相似性:
\( S_{ij} = \frac{W_{:,i}^\top W_{:,j}}{\| W_{:,i} \|2 \| W{:,j} \|2} \) (15)
其中,\( W{:,i} \)表示\( W \)的第\( i \)列。基于相似性矩阵\( S \),我们对方向一致的列进行聚类,形成更同构的块以进行三元量化。如图3(右图)所示,重排序降低了块内方差,表明块内权重分布更加紧凑。
与生成式预训练变压器量化(GPTQ)的高效集成:生成式预训练变压器量化(GPTQ)按块量化权重,每一步后应用误差补偿。这种块间依赖使得一次性基于聚类的重排序无效,而每次更新后重新聚类的成本又过高。为了在准确率和效率之间取得平衡,我们采用一种轻量级策略:每次更新后,从剩余子矩阵中计算均值参考\( \overline{w} = \frac{1}{m - k} \sum_{i=k}^{m-1} W_{:,i} \),并选择top-k个相似列,其中\( k \)是量化块大小:
\( \mathcal{B} = \text{Top-k} \left( \left\{ \frac{W_{:,i}^\top \overline{w}}{\| W_{:,i} \|_2 \| \overline{w} \|2} \right\}{i=k}^{m-1} \right) \)
这里,\( \overline{w} \)是剩余子矩阵的均值向量,\( \mathcal{B} \)包含top-k个最相似的列,形成下一个量化块。我们将这种轻量级策略称为基于结构相似性的重排序(SSR),它保留了重排序的优势,同时开销最小。
4 实验
4.1 实验设置
实现细节:所有实验均使用 PyTorch(Paszke 等人,2019b)和 Huggingface(Paszke 等人,2019a)框架,在单个 NVIDIA A800-80GB GPU 上进行。由于 PT²-LLM 是一种训练后量化框架,它不需要训练或梯度反向传播。借鉴 Li 等人(2025a)和 Huang 等人(2025)的方法,我们使用来自维基文本 2(Wikitext2)(Merity 等人,2017)数据集的 128 个校准样本,每个样本的序列长度为 2048。所有量化模型均使用固定的块大小 128。
模型与评估:我们在拉玛(LLaMA)(Touvron 等人,2023a)、拉玛 2(LLaMA-2)(Touvron 等人,2023b)、拉玛 3(LLaMA-3)(Dubey 等人,2024)系列以及较新的通义千问 3(Qwen3)系列(Yang 等人,2025)上进行了全面实验。借鉴先前的工作(Frantar 等人,2023;Lin 等人,2024b),我们从困惑度和准确率两个方面评估模型性能。我们在维基文本 2(Wikitext2)(Merity 等人,2017)和 C4(Raffel 等人,2020)数据集上报告困惑度(使用 2048 个标记的序列长度),并在 7 个广泛使用的问答基准数据集上评估零样本准确率:ARC-c(Clark 等人,2018)、ARC-e(Clark 等人,2018)、BoolQ(Clark 等人,2019)、HellaSwag(Zellers 等人,2019)、OBQA(Mihaylov 等人,2018)、PIQA(Bisk 等人,2020)和 Winogrande(Sakaguchi 等人,2020)。
基线:我们将 PT²-LLM 与多种具有代表性的、在 2 位和亚 2 位领域运行的训练后量化方法进行比较。精简大型语言模型(Slim-LLM)(Huang 等人,2025)作为混合精度量化的强基线,平均精度为 2 位,性能优异。部分二值化大型语言模型(PB-LLM)(Shang 等人,2024)面向亚 2 位领域,其平均位宽与我们的方法最接近,因此是相关基线。我们还纳入了广泛使用的基线生成式预训练变压器量化(GPTQ)(Frantar 等人,2023)和激活感知权重量化(AWQ)(Lin 等人,2024b),以及面向 2 位量化的量化与不连贯处理(QuIP)(Chee 等人,2025)。
表 1:多个大型语言模型骨干网络的评估。我们报告了维基文本 2 和 C4 数据集上的困惑度(PPL),以及 7 个零样本任务的准确率(%)。所有量化模型均使用 128 的块大小。最佳和次佳结果(不包括 FP16)分别用粗体和下划线标记。
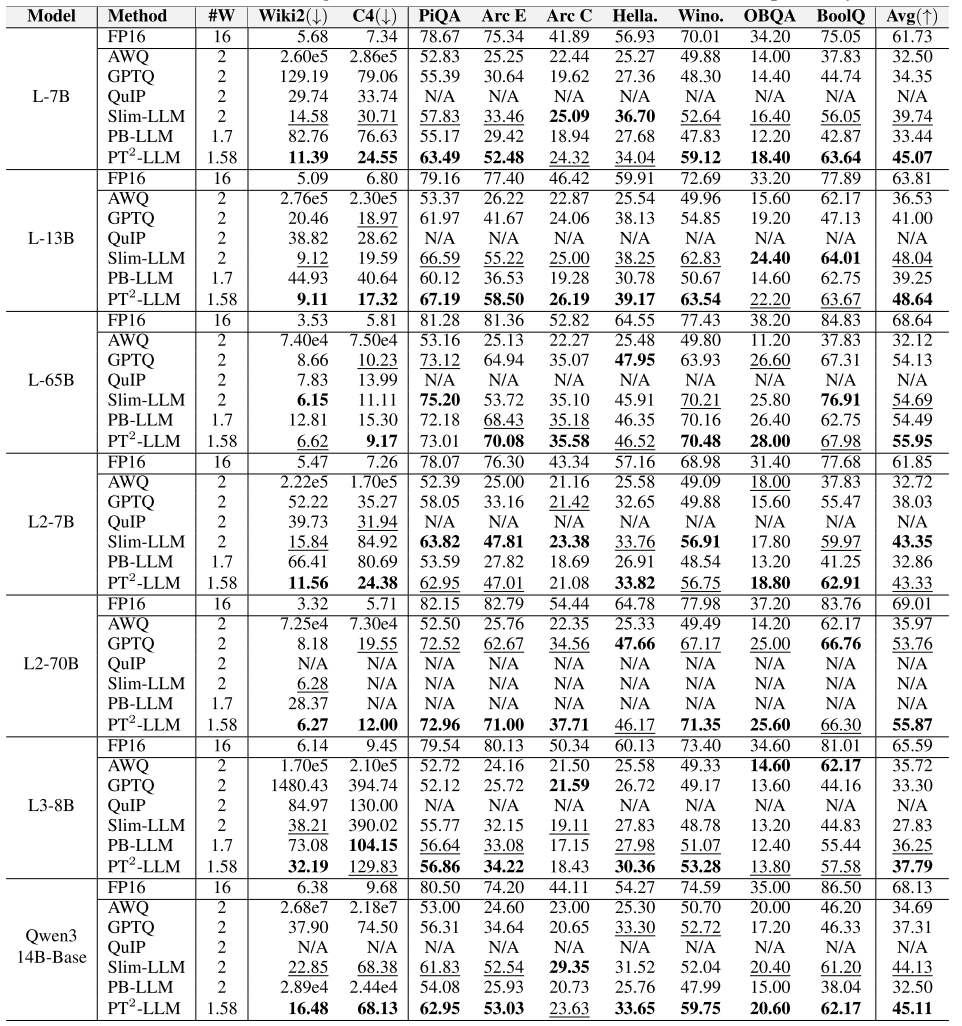
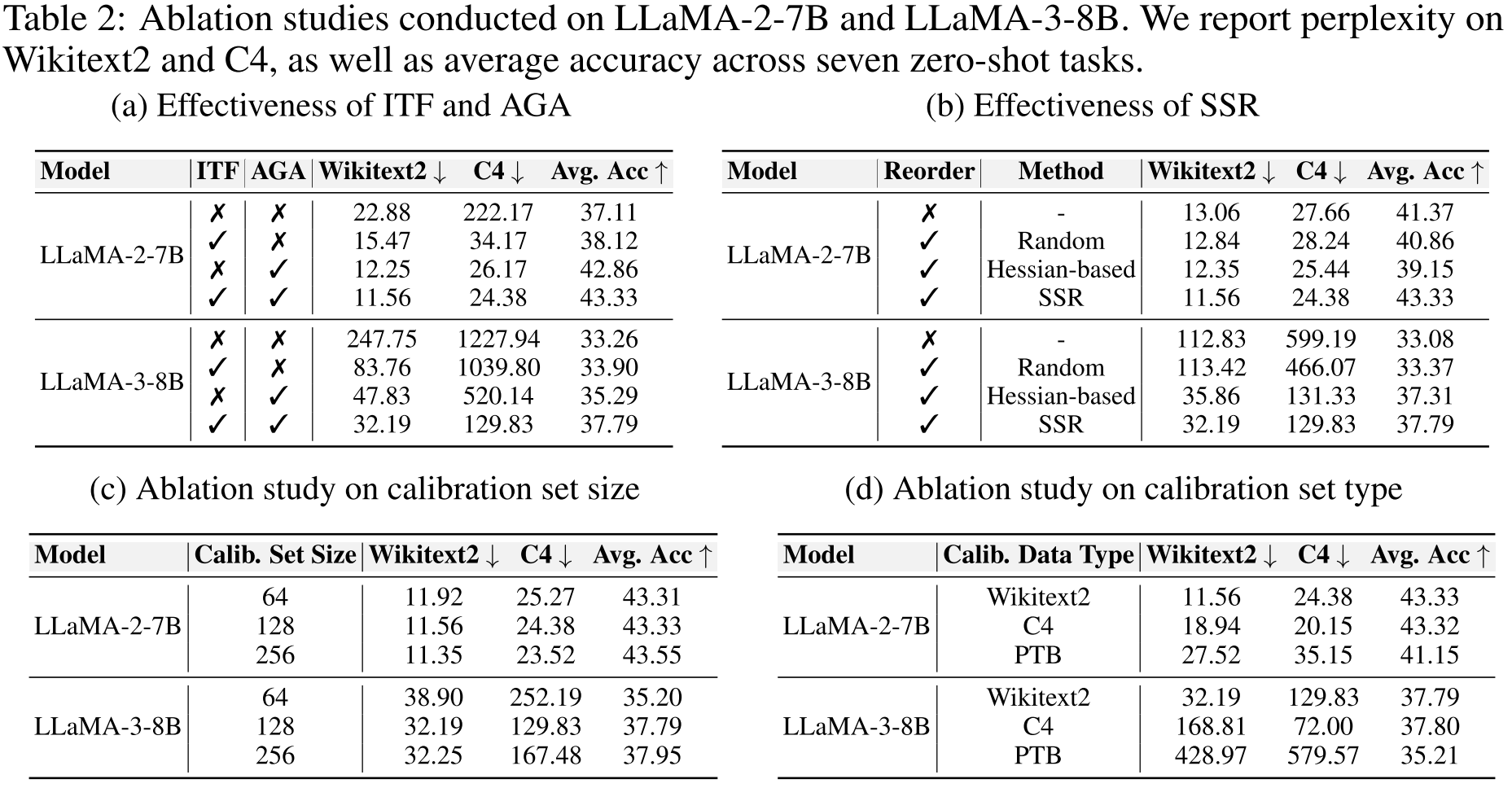
表 2:在拉玛 2-7B 和拉玛 3-8B 上进行的消融实验。我们报告了维基文本 2 和 C4 数据集上的困惑度,以及 7 个零样本任务的平均准确率。(a)迭代三元拟合(ITF)和激活感知网格对齐(AGA)的有效性;(b)基于结构相似性的重排序(SSR)的有效性;(c)校准集大小的消融实验;(d)校准集类型的消融实验。
4.2 与最先进方法的比较
表 1 总结了 PT²-LLM 和基线方法在拉玛(LLaMA)、拉玛 2(LLaMA-2)、拉玛 3(LLaMA-3)和通义千问 3-base(Qwen3-base)上的结果,报告了维基文本 2/C4 数据集上的困惑度、7 个任务的零样本准确率(含平均值)以及平均位宽。尽管 PT²-LLM 的位宽最低(1.58 位),但在所有模型尺寸下,其在困惑度和平均准确率方面均稳居前两名。它明显优于 2 位基线方法,如生成式预训练变压器量化(GPTQ)、激活感知权重量化(AWQ)和量化与不连贯处理(QuIP)。与当前最先进的 2 位方法精简大型语言模型(Slim-LLM)相比,除拉玛 2-7B 模型(性能相当)外,PT²-LLM 在所有模型上均实现了更高的平均准确率。与位宽相当的部分二值化大型语言模型(PB-LLM)相比,PT²-LLM 带来了显著提升:在拉玛 7B 模型上,它将平均准确率从 33.44 提高到 45.07,将维基文本 2 数据集上的困惑度降低了 86%,并且所需内存更少。补充材料中提供了更多结果。
4.3 消融实验
迭代三元拟合(ITF)和激活感知网格对齐(AGA)的有效性:我们对非对称三元量化器进行了分解消融实验,重点关注其两个组件:迭代三元拟合(ITF)和激活感知网格对齐(AGA)。如表 2a 所示,迭代三元拟合(ITF)和激活感知网格对齐(AGA)均比基线带来了性能提升。例如,在拉玛 2-7B 模型上,迭代三元拟合(ITF)将维基文本 2 数据集上的困惑度从 22.88 降低到 15.47,而激活感知网格对齐(AGA)将平均准确率从 37.11 提高到 42.86。当两者结合使用时,取得了最佳的整体性能,突显了它们的互补优势,验证了我们的设计合理性。
基于结构相似性的重排序(SSR)的有效性:我们评估了基于结构相似性的重排序(SSR)对量化性能的影响。如表 2b 所示,省略重排序会导致次优结果,因为三元量化对分散权重和异常值高度敏感。随机重排序的效果微乎其微,而基于黑塞矩阵的重排序虽然偶尔有效,但往往忽略了块级三元量化的结构挑战。相比之下,我们提出的基于结构相似性的重排序(SSR)通过促进列间相似性,实现了块内权重分布的更紧凑性,并降低了块级三元量化对异常值的敏感性,因此始终能产生更优异的性能。
校准集大小的消融实验:我们评估了校准集大小对 PT²-LLM 性能的影响。如表 2c 所示,更大的数据集在困惑度和准确率方面带来了适度提升。虽然 64 个样本会导致性能略有下降,但使用 128 或 256 个样本会产生几乎相同的结果,表明一旦达到适度阈值,PT²-LLM 对校准集大小具有很强的稳健性。考虑到性能和内存效率之间的权衡,我们在所有实验中采用 128 个样本,这证明了 PT²-LLM 在资源受限场景下的实用性。
校准集类型的消融实验:我们通过在三个数据集(维基文本 2、C4 和 PTB)上进行消融实验,研究了校准数据集选择对量化的影响。如表 2d 所示,使用维基文本 2 或 C4 数据集导致了相当的平均准确率,而 PTB 数据集的性能明显更差,这可能是由于其数据质量较低。此外,在维基文本 2 或 C4 数据集上进行校准,能够提高它们各自数据集上的困惑度,显示出明显的域内优势。考虑到所有指标,并借鉴先前的工作(如精简大型语言模型(Slim-LLM)(Huang 等人,2025)),我们选择维基文本 2 作为校准集。
4.4 压缩时间和模型大小分析
我们将 PT²-LLM 与生成式预训练变压器量化(GPTQ)、精简大型语言模型(Slim-LLM)、部分二值化大型语言模型(PB-LLM)以及两种二值化方法(二元大型语言模型(BiLLM)(Huang 等人,2024)和交替精炼二值化大型语言模型(ARB-LLM)(Li 等人,2025b))在压缩时间和模型大小方面进行了比较。
压缩时间:如表 3 所示,PT²-LLM 在质量和效率之间取得了良好的平衡。压缩拉玛 7B 模型仅需 32 分钟,明显快于精简大型语言模型(Slim-LLM)(182 分钟)、二元大型语言模型(BiLLM)(45 分钟)和交替精炼二值化大型语言模型(ARB-LLM)(88 分钟)。虽然比生成式预训练变压器量化(GPTQ)和部分二值化大型语言模型(PB-LLM)稍慢,但考虑到性能的提升,这种开销仍然是适度且可接受的。
模型大小:如表 3 所示,PT²-LLM 实现了最小的模型大小(拉玛 7B 模型为 1.88 GB),与 FP16 相比压缩比达到 7.17 倍。它超过了生成式预训练变压器量化(GPTQ)(6.16 倍)、精简大型语言模型(Slim-LLM)(5.86 倍)和部分二值化大型语言模型(PB-LLM)(4.63 倍),甚至优于二值化方法,如二元大型语言模型(BiLLM)(4.60 倍)和交替精炼二值化大型语言模型(ARB-LLM_X)(4.17 倍),这些二值化方法的压缩比受到复杂位图设计开销的限制。补充材料中提供了关于内存构成和存储分解的详细讨论。
表 3:拉玛 7B 模型上各种量化方法的模型大小、压缩比和压缩时间比较,突出了 PT²-LLM 相对于现有方法的效率。

4.5 推理速度评估
如图 4 所示,我们使用 llama.cpp 框架,在 NVIDIA A800 GPU 上评估了四种模型规模(拉玛 7B 至 65B)的推理吞吐量,序列长度分别为 128(预填充)、256(解码)和 128+256(端到端)。与标准 2 位量化相比,我们的 1.58 位 PT²-LLM 在所有三个阶段均持续提高了吞吐量,并在拉玛 65B 模型的端到端生成中实现了高达 2.1 倍的加速。补充材料中提供了实验细节。
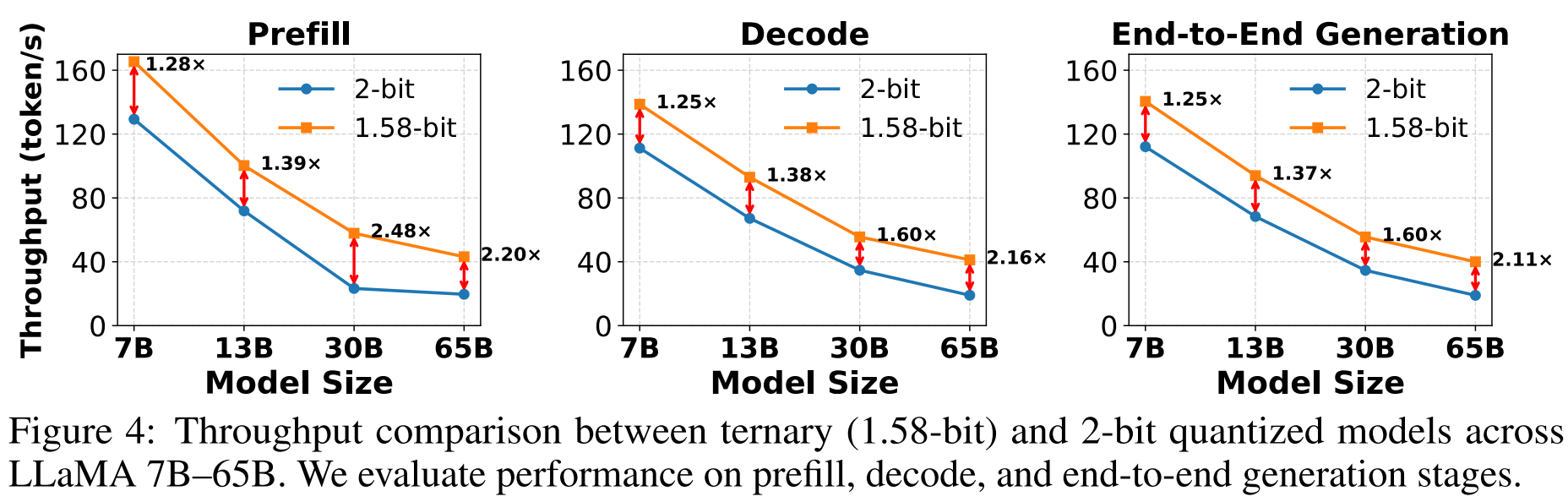
图 4:三元(1.58 位)和 2 位量化模型在拉玛 7B--65B 模型上的吞吐量比较。我们评估了预填充、解码和端到端生成阶段的性能。
5 结论
在本文中,我们提出 PT²-LLM,一种专为大型语言模型设计的训练后三元量化框架。我们的方法提出了一种具有两阶段流水线的非对称三元量化器(ATQ),其中迭代三元拟合(ITF)以无训练方式降低量化误差,激活感知网格对齐(AGA)使三元输出更紧密地与全精度输出对齐。我们进一步提出基于结构相似性的重排序(SSR),一种即插即用的策略,能够降低量化难度并减轻异常值的影响。实验结果表明,与最先进的 2 位训练后量化方法相比,PT²-LLM 获得了具有竞争力的准确率,同时减小了模型大小并加速了推理。这项工作为大型语言模型训练后量化场景中的三元量化建立了强大的基线,推动了亚 2 位压缩的边界,并为未来的研究奠定了基础。