TL;DR
在使用最小二乘法求解线性回归时，多重共线性会影响模型稳定性，导致系数估计不可靠。解决方法包括使用正则化技术（如岭回归、Lasso回归）。通过引入正则化项，可以有效避免矩阵不可逆问题，稳定回归结果。
版本矩阵
| 功能 | scikit-learn 版本 | 说明 |
|---|---|---|
| 线性回归 | 0.24+ | 支持标准的线性回归模型训练与评估 |
| 多重共线性处理 | 0.24+ | 通过岭回归、Lasso回归等方法解决共线性问题 |
| MSE计算 | 0.24+ | 使用 mean_squared_error 计算模型误差 |
| R²计算 | 0.24+ | 使用 r2_score 评估模型拟合度 |
代码实现
使用 scikit-learn 算法库实现线性回归算法，并计算相应评价指标。回顾前文介绍的相关知识进行下述计算。
python
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(data.iloc[:,:-1].values,data.iloc[:,-1].values)
reg.coef_ # 查看方程系数
reg.intercept_ # 查看系数对比手动计算的 ws，其结果高度一致。 然后计算模型 MSE 和判别系数：
python
from sklearn.metrics import mean_squared_error,r2_score
yhat = reg.predict(data.iloc[:,:-1])
mean_squared_error(y,yhat)
r2_score(y,yhat)多重共线性
虽然在线性回归求解过程中，通过借助最小二乘法能够迅速找到全域最优解，但最小二乘法本身的使用条件较为苛刻。这种方法要求设计矩阵X必须满足严格的条件才能保证解的稳定性和唯一性。
具体来说，最小二乘法的应用必须满足以下关键条件：
- 矩阵X^TX必须是满秩矩阵（即行列式不为零）
- 矩阵X^TX必须可逆或存在广义逆矩阵
在实际应用中，经常会遇到以下导致最小二乘法失效的情况：
- 当样本量n小于特征数p时（n<p），矩阵X^TX必然是奇异矩阵
- 当X的各列存在严格或近似的线性相关关系时（即多重共线性问题）
- 当数据中存在高度相关的特征变量时
特别是当遇到多重共线性问题时，最小二乘法的求解会面临以下挑战：
- 参数估计值变得极不稳定，小的数据扰动可能导致估计值发生巨大变化
- 参数估计的方差会异常增大
- 解可能不唯一，存在无穷多解的情况
例如，在经济学数据分析中，当使用GDP、居民收入和消费支出等多个高度相关的指标作为预测变量时，就很容易出现上述问题。此时传统的OLS（普通最小二乘）估计将无法给出可靠的结果。
针对这些问题，统计学家们发展出了多种改进方法，包括：
- 岭回归（Ridge Regression）
- Lasso回归
- 主成分回归（PCR）
- 偏最小二乘回归（PLSR）
这些方法通过引入正则化项或降维技术，可以有效处理矩阵不可逆和多重共线性问题，从而获得更稳定可靠的回归结果。
这里需要注意是，在进行数据采集的过程中，数据集各列是对同一个客观事物进行客观描述，很难避免多重共线性的存在，因此存在共线性是很多数据集的一般情况。当然更为极端的情况则是数据集的列比行多，此时最小二乘法无法对其进行求解。因此，寻找性回归算法的优化方案势在必行。 首先我们来了解多重共性，在第二节中我们曾推导了多元线性回归使用最小二乘法的求解原理，我们对多元线性回归的损失函数求导，并得出求解系数 w 得式子和过程：
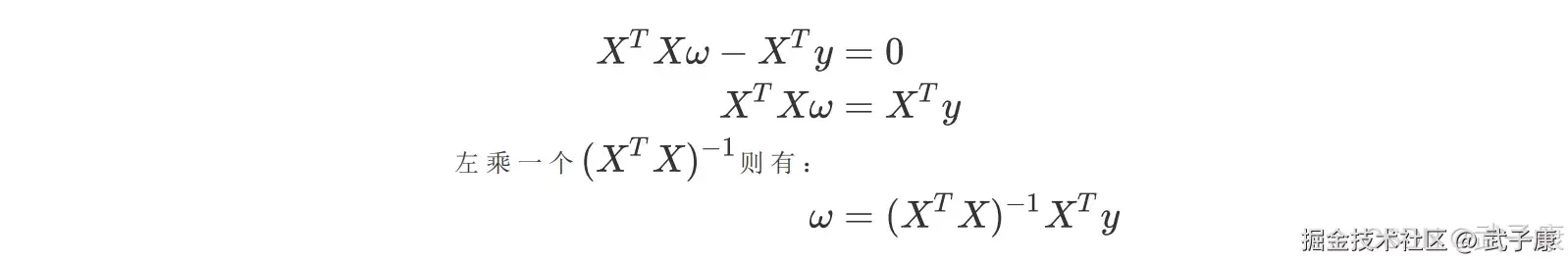在最后一步中我们需要左乘 XTX 的逆矩阵，而矩阵存在得充分必要条件是特征不存在多重共线性。
矩阵存在的充分必要条件
首先，我们需要先理解逆矩阵存在与否的意义和影响，一个矩阵什么情况下会有逆矩阵？ 根据逆矩阵的定理，若 |A| != 0，则矩阵A 可逆，且：
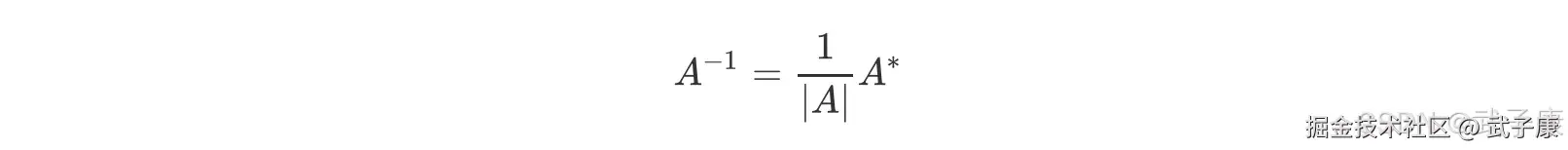
其中 A* 是矩阵 A 的伴随矩阵，任何矩阵都可以有伴随矩阵，因此这一部分不影响逆矩阵的存在性，而分母上行列式｜A｜就不同了，位于分母变量不能为 0，一旦为 0 则无法计算出逆矩阵。因此逆矩阵存在的充分必要条件是：矩阵的行列式不能为 0，对于线性回归而言，即是说｜XTX｜不能为 0，这是使用最小二乘法求解线性回归的核心条件之一。
行列式不为 0 的充分必要条件
那行列式不为 0，需要满足什么条件？在这里，我们复习一下线性代数中的基本知识，假设我们的特征矩阵 X结构为（m,n），则 XTX 就是结构为（n,m）的矩阵，从而得到结果为（n,n）的矩阵。
因此以下所有的例子都将以方矩阵进行举例，方便大家理解，首先区别一下矩阵和行列式： 
任何矩阵都可以有行列式，以一个 3*3 的行列式为例，我们来看看行列式如何计算的？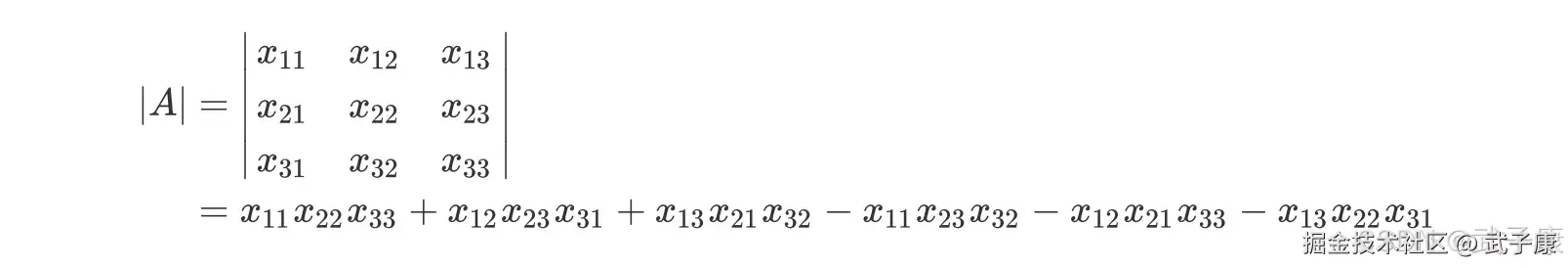 
这个式子乍一看非常混乱，其实并非如此，我们把行列式按照下面的方式排列一下，很容易就看出这个式子实际上怎么回事了： 
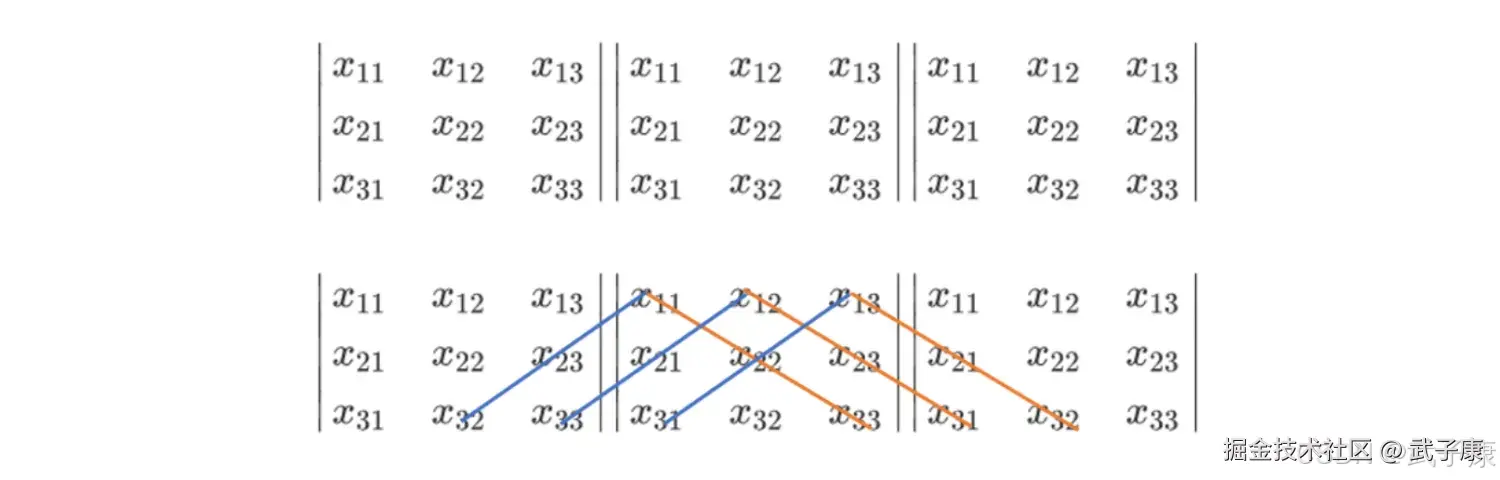三个特征的特征矩阵的行列式就有六个交互项，在现实中我们特征矩阵不可能是如此低维度数据，因此使用这样的方式计算就变得异常困难。在线性代数中，我们可以通过行列式的计算将一个行列式整合成一个梯形的行列式： 
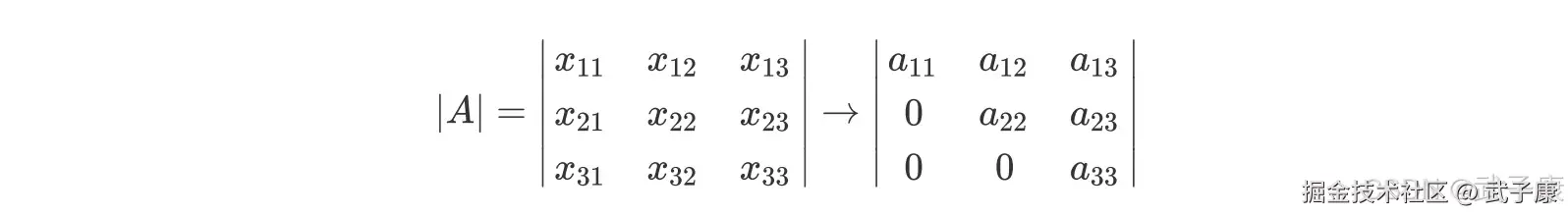梯形的行列式表现为，所有的数字都被整合到对角线的上方或下方（通常是上方），虽然具体的数字发生了变化（比如由 x11 变成了 a11），但是行列式的大小在初等行变换的过程中是不变的，对于梯形行列式，行列式的计算要容易的多： 
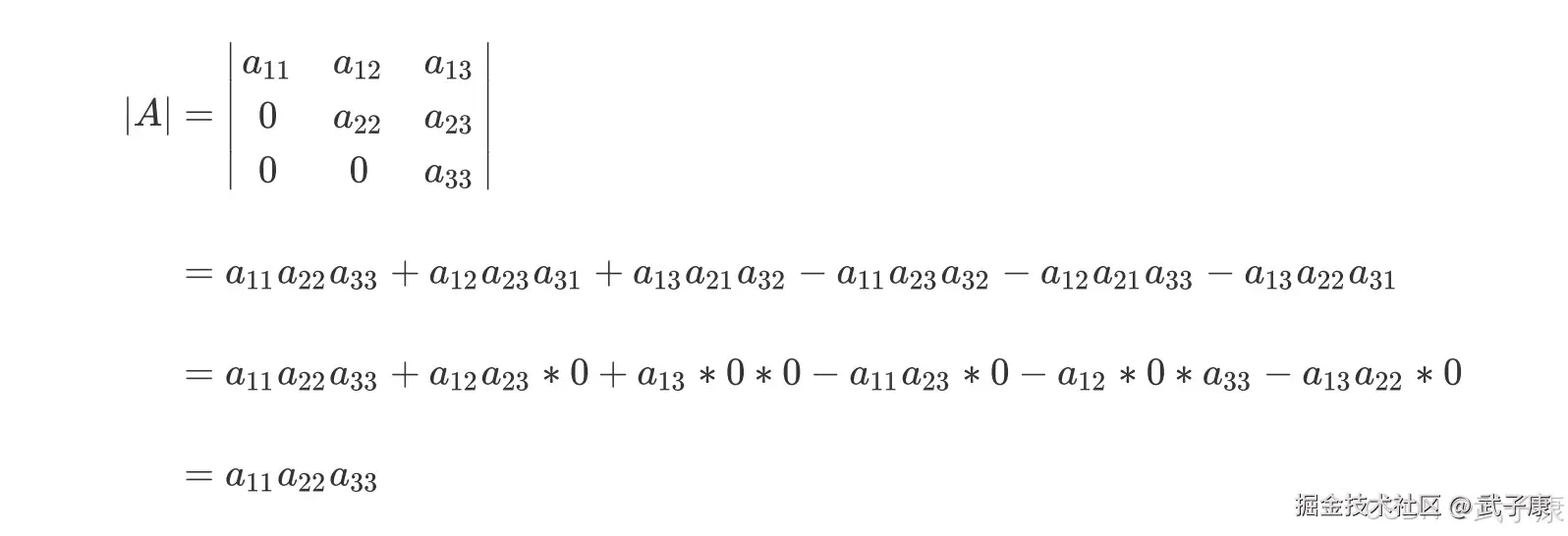不难发现，由于梯形行列式下半部分为 0，整个矩阵的行列式其实就是梯形行列式对角线上的元素相乘。并且此时时刻，只要对角线上的任意元素为 0，整个行列式都会为 0，那只要对角线上没有一个元素为 0，行列式就不会为 0。在这里我们映入一个重要的概念：满秩矩阵。
矩阵满秩的充分必要条件
一个矩阵要满秩，则转换为梯形矩阵后的对角线上没有 0，那什么样的矩阵在对角线上没有 0？来看下面的三个矩阵：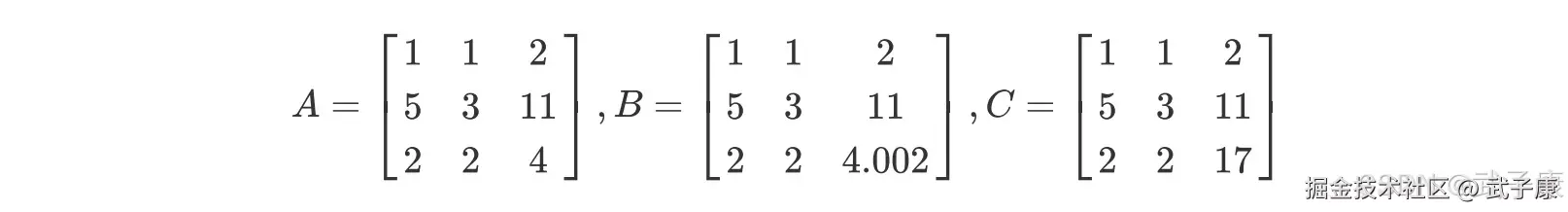 
我们可以对矩阵做初等行变换和列变换，包括交换行/列顺序，将一列/一行乘以用一个常数后加减到另一个一列/一行上，来将矩阵化为梯形矩阵，对于上面的两个矩阵我们可以有如下变换： 
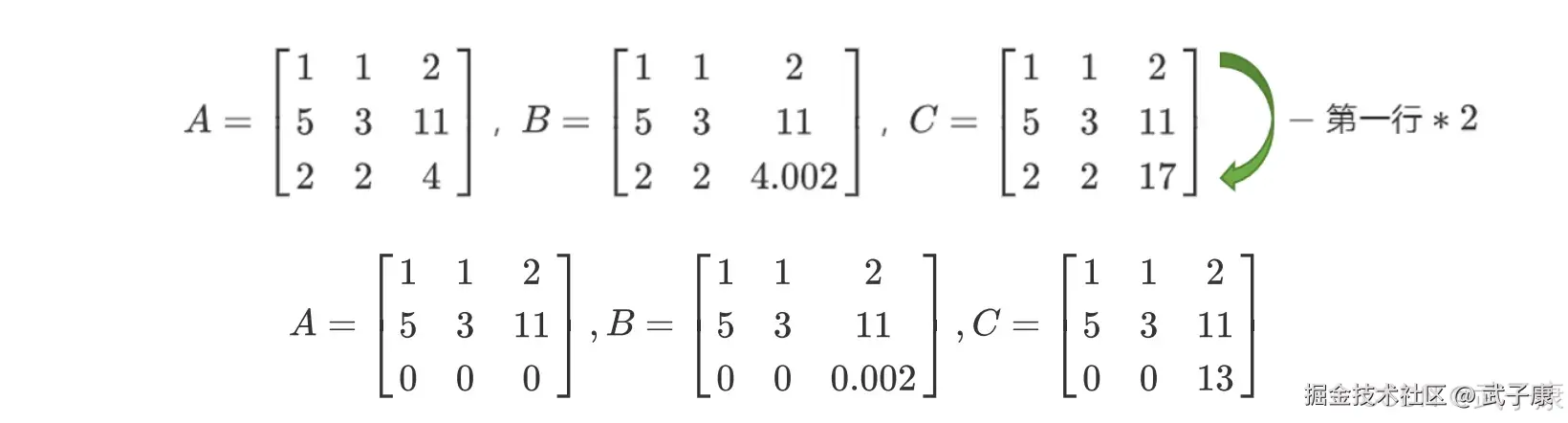继续进行变换： 
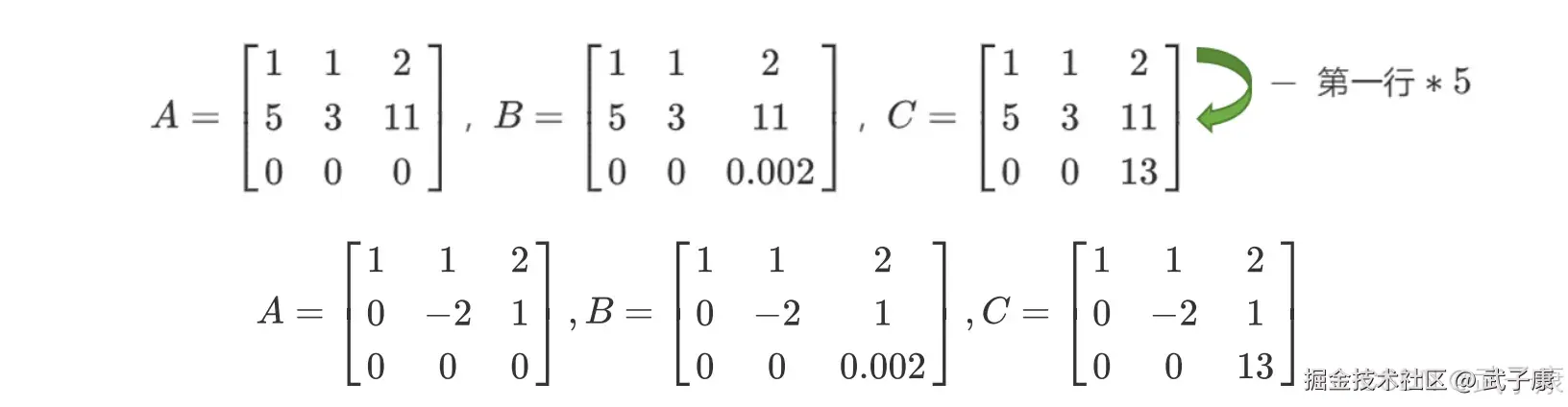如此就转换成了梯形矩阵，我们可以看到，矩阵 A 明显不是满秩的，它有全零行所以行列式会为 0，而矩阵 B 和 C 没有全零行所以满秩。 而矩阵 A 和矩阵 B 的区别在于，A 中存在完全具有线性关系的两行（1,1,2 和 2,2,4），而 B 和 C 中则没有这样的两行。 而矩阵 B 虽然对角线上每个元素都不为 0，但具有非常接近于 0 的元素 0.02，而矩阵 C 的对角线上没有任何元素特别接近于 0。
矩阵 A 中第一行和第三行的关系，被称为：精确相关关系，即完全相关，一行可使另一行为 0，在这种精确相关关系下，矩阵 A 的行列式为 0，则矩阵 A 的逆不可能存在。在我们的最小二乘法中，如果矩阵 XTX 中存在这种精确相关关系，则逆不存在，最小二乘法完全无法使用，线性回归会无法求出结果。
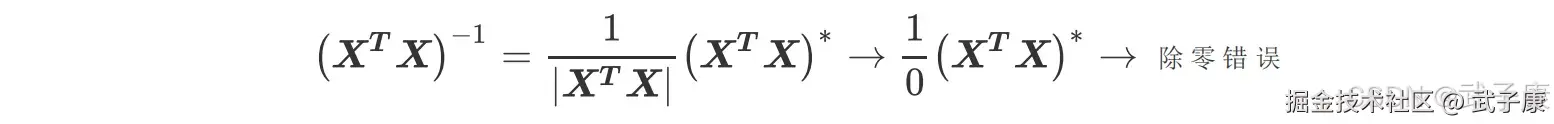矩阵 B 中第一行和第三行的关系不太一样，他们之间非常接近于精确相关关系，但又不是完全相关，一行不能使领一行为 0，这种关系被称为 高度相关关系。这种高度相关关系下，矩阵的行列式不为 0，但是一个非常接近 0 数，矩阵 A 的逆存在，不过接近于无限大。在这种情况下，最小二乘法可以使用，不过得到的逆会很大，直接影响我们对参数向量 w 的求解：
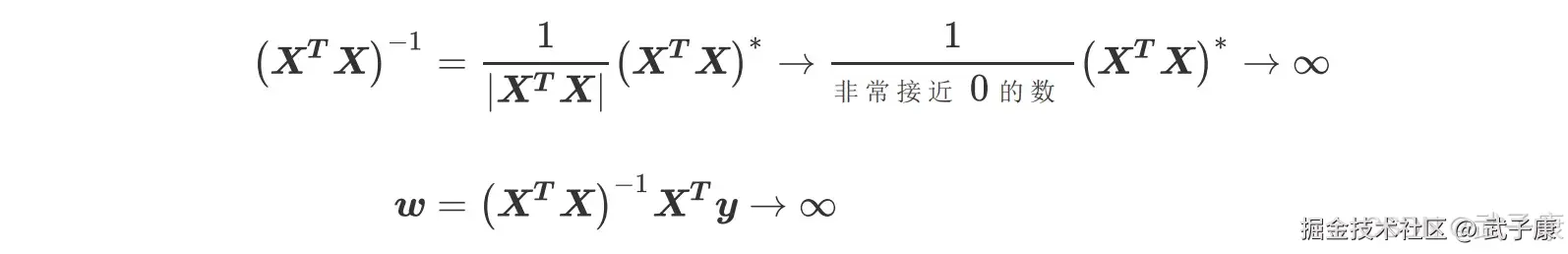这样求解出来的参数向量 w 会很大，因此会影响建模的结果，造成模型有偏差或者不可用。精确相关关系和高度相关关系并称为多重共线性。在多重共线性下，模型无法建立，或者模型不可用。 相对的，矩阵 C 的行之间结果相互独立，梯形矩阵看起来非常正常，它的对角线上没有任何元素特别接近于 0，因此其行列式也就不会接近0 或者为 0，因此矩阵 C 得出的参数向量 w 就不会有太大的偏差，对于我们拟合而言是比较理想的。
从上面的所有过程我们可以看得出来，一个矩阵如果要满秩，则要求矩阵中每个向量之间不能存在多重共线性，这也构成了线性回归算法对于特征矩阵的要求。
错误速查
| 症状 | 根因 | 定位 | 修复 |
|---|---|---|---|
| 模型参数估计不稳定 | 数据中存在多重共线性，导致设计矩阵 X^T X 不可逆 | 检查特征变量之间是否存在线性相关关系 | 使用岭回归、Lasso回归等正则化方法来稳定解 |
| 模型方差过大 | 矩阵 X^T X 近似奇异或共线性问题 | 查看矩阵的行列式，确认是否接近零 | 引入正则化项，如岭回归，来减少参数方差 |
| 预测结果误差较大 | 多重共线性导致解的不唯一性 | 确认特征变量是否高度相关，尤其是输入数据集 | 使用主成分回归（PCR）或偏最小二乘回归（PLSR） |
| 解不唯一 | 矩阵 X^T X 为奇异矩阵，无法求逆 | 检查输入数据集的特征数是否大于样本数（n<p） | 减少特征数，或使用正则化方法来规避该问题 |
其他系列
🚀 AI篇持续更新中（长期更新）
AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架 私有部署 测试上手 架构研究 ，持续打造实用AI工具指南！ AI研究-132 Java 生态前沿 2025：Spring、Quarkus、GraalVM、CRaC 与云原生落地
💻 Java篇持续更新中（长期更新）
Java-218 RocketMQ Java API 实战：同步/异步 Producer 与 Pull/Push Consumer MyBatis 已完结，Spring 已完结，Nginx已完结，Tomcat已完结，分布式服务已完结，Dubbo已完结，MySQL已完结，MongoDB已完结，Neo4j已完结，FastDFS 已完结，OSS已完结，GuavaCache已完结，EVCache已完结，RabbitMQ已完结，RocketMQ正在更新... 深入浅出助你打牢基础！
📊 大数据板块已完成多项干货更新（300篇）：
包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！ 大数据-278 Spark MLib - 基础介绍 机器学习算法 梯度提升树 GBDT案例 详解