论文:Loy, G., & Zelinsky, A. (2002). A fast radial symmetry transform for detecting points of interest. Computer Vision, ECCV 2002.
注意:这份开源代码中的gradx和grady算反了
1. 图像梯度理解
对灰度图像I(x,y) ,梯度(Gradient)定义为,梯度变化反应灰度图像的明暗走向。
表示左右方向梯度变化,表示上下方向梯度变化。
梯度幅值(Magnitude ):
梯度方向(Orientation) :
对比度高的区域梯度大:例如一个黑色物体放在白色背景上,边缘非常清晰,像素值从0(黑)瞬间跳变为255(白),梯度变化很大,类似悬崖的坡度。
模糊区域梯度小:物体边缘有阴影过渡,像素值不是瞬间变化的,而是慢慢变的,类似平缓的坡道。
关于噪声的梯度:
- 普通背景噪声(梯度小):来源于相机的热噪声或者光照不均,例如原本是纯黑区域(0),实际上像素值是乱跳如2,5,3,4,1。相邻像素的梯度只有2-3左右,但真正物体的边缘梯度可能在50甚至100以上。
- 椒盐噪声/坏点(梯度大):假如相机有一个坏点,纯黑背景上出现一个亮点。0->255->0导致梯度很大,比正常物体的边缘还要大。
2. FRST思想
直觉:对于每一个径向对称的物体,其边缘上的每一点,梯度方向都会指向圆心(亮中心)或者背离圆心(暗中心)。
做法:遍历图像中每一个像素,沿着梯度方向延伸一段距离n(半径),落脚点很可能就是圆心。如果大量像素的梯度延长线都交汇与一点,那么这一点就是对称中心。
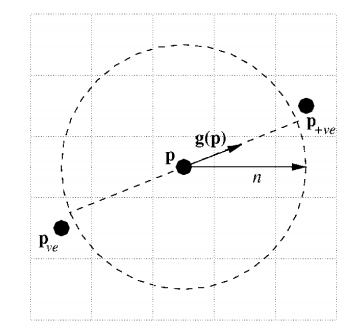
对于图像上任意一个像素p,沿着梯度方向、距离为n的位置认为是亮圆圆心(正向投票),相反方向距离为n的位置认为是暗圆圆心(负向投票)
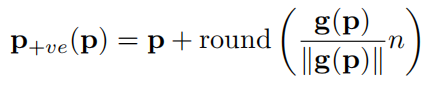
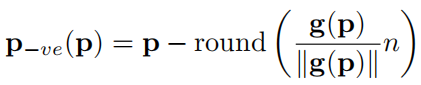
表示梯度方向,
则表示偏移量,由于像素是整数,四舍五入取整后即得到与p像素梯度方向距离为n的最近的点的像素位置。
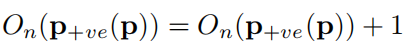
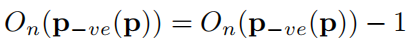
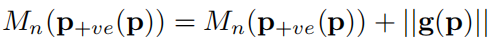
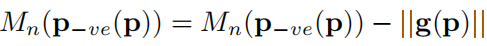
遍历完全图会生成两张图像用于投票:方向投影图、幅度投影图
。
- 对于
:图像初始状态全为0,遍历时,对于每一个像素p,计算出
和
,然后在图像中
位置的矩阵值就+1,
位置的矩阵值就-1,所以
类似计数器,表示有多少个像素指向这个位置。
- 对于
:图像初始状态全为0,遍历时,对于每一个像素p,计算出
和
,然后在
图像中
位置的矩阵值就+p的梯度幅值,
位置的矩阵值就-p的梯度幅值,所以
也是累计图,表示指向这个位置的梯度总强度是多大。
直觉上,图像最大正值的位置最可能是亮圆中心,最小负值位置最可能是暗圆中心。但是图像的噪声会导致梯度随机波动,随机梯度有概率在某些点偶然交汇,这些噪点并不具备真实的几何对称性,但这些噪点平等的参与投票,一个微弱的噪声边缘(梯度很小)和一个强烈的物体边缘(梯度很大),贡献都是1,这其实是不公平的,仅用
很大概率会投出错误的圆心。仅用
更不行,
只关注梯度强度,梯度很大,确认是对比度高的边缘,但这个边缘可能不是圆。
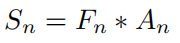
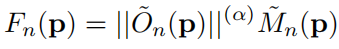
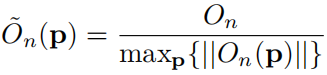
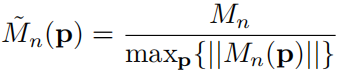
所以将和
结合起来,理论上可以找到梯度大的对称区域,
就是融合两者的方法。
对于公式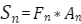 ,
,是未经平滑的原始的对称响应图,
是一个二维高斯卷积核,用来平滑图像。
不仅通过乘法操作融合
和
,并且通过指数加权α抑制噪声,放大真正的结果。如果只有
票数没有强度
,那么乘法的得分低,如果只有强度
没有票数
,乘法的得分也低,只有两者都大,乘法结果才巨大。假设α=2,噪点位置有2个像素指向它(
=2)则指数加权后的结果是4,真圆心位置有50个像素指向它(
=50)则指数加权后的结果是2500,通过α指数,可以瞬间拉开目标特征与噪声之间的得分距离。当然公式中并不是用直接进行指数加权的,而是进行归一化后再进行加权。
和
表示对和中绝对值最大的,则和被归一化到[-1, 1],再进行指数加权。
标准数学符号里,通常表示绝对值或者范数,结果是正的。在这篇论文中定义了一种特殊的运算符号:,表示先取绝对值做α次方,再把原来的正负号乘回去。如果不保留符号,所有暗圆经过平方(如果α=2)后都变成正的,就分不清暗圆和亮圆了。
在计算出后用
进行卷积的主要原因是:1)解决离散化误差;2)进一步抑制噪声。在做梯度投影时使用了round,但如果真正的圆心在(50.5,50.5),投影结果会一部分落在(50,50),一部分落在(51,51),会导致
图中的能量被撕裂了,高斯卷积
可以把(50,50)和(51,51)这两个相邻的峰值合并成一个位于(50.5,50.5)附近的单一波峰。另外,尽管α参数已经抑制了很多噪声,但
图中可能还是会有孤立的、高频的随机响应。高斯平滑会压低孤立尖峰,保留成片有结构支撑的响应区域。
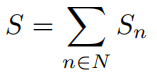
半径为n(n∈N)的所有都将会被叠加到一张图上,核心动机是为了解决尺度未知的问题。假如只计算了
(半径为5),如果图像中的圆刚好半径是5,可以得到一个极强的亮点,这没有问题,但如果图像中的圆半径是5.5或者4.5,由于算法中的投票机制非常精确,半径稍微对不上,票数就会急剧下降,导致漏检或者低响应。
求和可以检测半径大小在N范围内的所有圆,假如图像中圆的半径是5.2,这个圆在
中有较高的响应,在
中也有不错的响应,如果计算,这个圆心的位置就会获得叠加的能量,在重叠的地方,形成一个非常显著的峰值。
3. FRST应用

图(c)n=1,3,5效果与图(b)n=1,2,3,4,5近似逼近,但计算量减小了。N范围小的时候计算量减小的不明显,N范围大计算量就有优势。如果知道圆的先验半径,只需要确定适当范围即可高效检测该特征。如图(d),瞳孔半径为5像素,已经能够检测出来。

单个梯度元素g(p)的贡献度
对于高斯核的选取。高斯核的核心作用是根据距离n的远近,扩散受正负影响像素的辐射范围。选择二维高斯核是因为其具有径向对称性,能对所有梯度方向产生统一影响,同时具备可分离性,使得卷积运算效率更高。通过将标准差与距离n进行线性比例调整,定义了覆盖所有受影响像素的辐射弧。该辐射弧的宽度由An的标准差与n的比值决定。
是一个大小为nxn、标准差σ=0.25n的高斯核。没有
的话,对于位置p的边缘像素,投票结果只是两个孤零零的像素点,会非常尖锐离散。加上
后,这两个点会在正梯度方向形成亮斑,在负梯度方向形成暗斑。高斯模糊表达了一种不确定性,圆心大概在这个区域,离中心越近概率越大,离得远也有可能。作者设定σ=0.25n以及kernel size为10,是用于尺度自适应。如果找n=2的小圆,σ=0.5,模糊范围很小,要求精度很高。如果找n=100的大圆,σ=25,模糊范围很大,大圆的边缘通常比较长,更容易变形或者受噪声影响,则需要更大宽容度让周围的票汇聚在一起。

参数α的选取。较高的α值会消除非径向对称特征(如线条),α=2的选择适用于大多数应用场景。α值越高,对关键点的衰减越明显,而α值过低则会过度强调非径向对称特征。但若将α值设为1,则可最小化方程中的计算量。

引入梯度阈值参数β。梯度元素的幅值较小时,其方向可靠性较低,更容易受到噪声干扰,且往往对应于人眼难以直接察觉的特征。由于变换的目的是提取图像中的关键点,因此在计算过程中忽略此类元素是合理的。当计算图像和
时,所有幅值低于 β 的梯度元素均被忽略。
非零 β 的主要优势在于提升算法速度,因为需要处理的梯度元素减少,从而降低受噪声影响的像素数量。该变换可调谐以仅检测对称性中的暗区或亮区。若仅需检测暗区,确定和
时只需考虑受噪声负面影响的像素(调整前面的公式)。同理,若仅需检测亮区对称性,则只需考虑受噪声正向影响的像素。
4. FRST性能表现
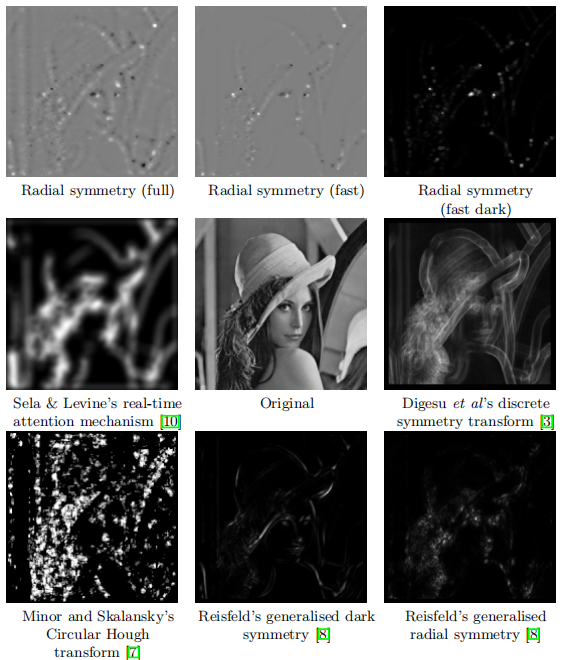
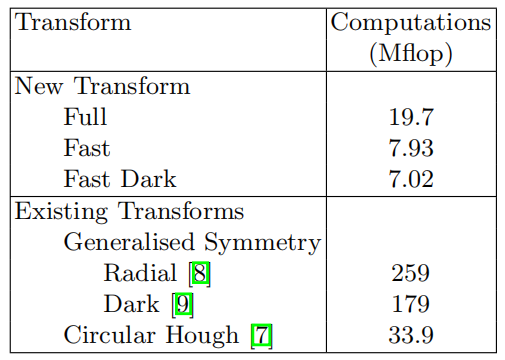
在测试图像中展现出与传统方法相当甚至更优的性能,同时显著降低了计算成本和实现复杂度。