**Hi，大家好，我是半亩花海。在上节说明了迁移学习领域的++条件分布自适应++ 之后，本文主要将介绍迁移学习的第一类方法------数据分布自适应，重点阐述了联合分布自适应(JDA)**的原理与应用。该方法通过同时减小源域和目标域的边缘分布和条件分布差异来实现迁移。JDA的核心思路是利用最大均值差异(MMD)距离来对齐两个域的分布，其中条件分布通过伪标签进行近似估计。另外，该方法采用迭代优化策略，逐步改进伪标签质量。
目录
[2.1 边缘分布适配](#2.1 边缘分布适配)
[2.2 条件分布适配](#2.2 条件分布适配)
[2.3 TCA 与 JDA 的比较](#2.3 TCA 与 JDA 的比较)
一、基本思路
联合分布自适应方法 (Joint Distribution Adaptation) 的目标是减小源域和目标域的联 合概率分布的距离，从而完成迁移学习。从形式上来说，联合分布自适应方法是用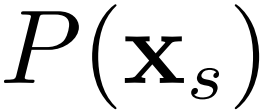 
和 
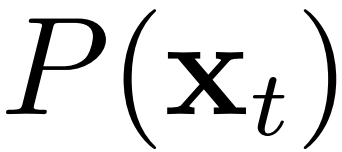之间的距离、以及 
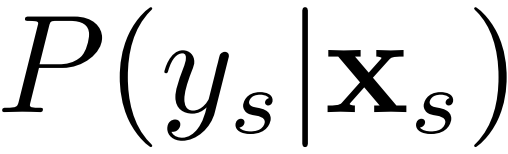和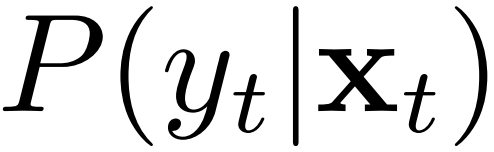 
之间的距离来近似两个领域之间的差异。即：
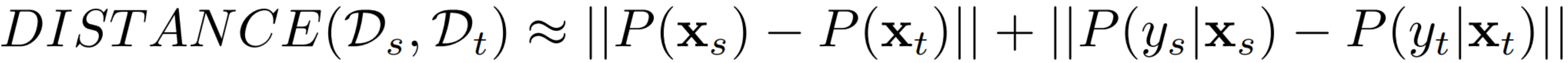
联合分布自适应对应于下图中由(a)迁移到(b)的情形、以及(a)迁移到(c)的情形。
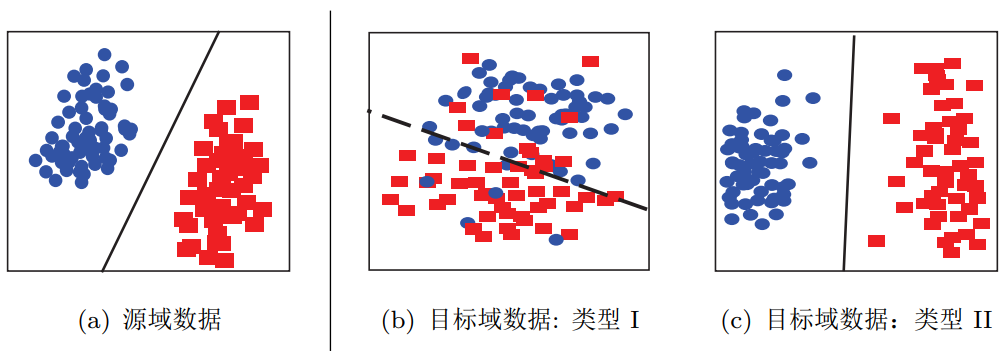不同数据分布的目标域数据
二、核心方法
联合分布适配的 JDA 方法 [Long et al., 2013] 首次发表于 2013 年的 ICCV(计算机视觉领域顶会，与 CVPR 类似)，它的作者是当时清华大学的博士生 (现为清华大学助理教授) 龙明盛。
假设是最基本的出发点。那么 JDA 这个方法的假设是什么呢？就是假设两点：1）源域和目标域边缘分布不同，2）源域和目标域条件分布不同。既然有了目标，同时适配两个分布不就可以了吗？于是作者很自然地提出了联合分布适配方法：适配联合概率。
不过这里我感觉有一些争议：边缘分布和条件分布不同，与联合分布不同并不等价。所以这里的"联合"二字实在是会引起歧义。我的理解是，同时适配两个分布，也可以叫联合， 而不是概率上的"联合"。尽管作者在文章里第一个公式就写的是适配联合概率，但是这里感觉是有一些问题的。我们抛开它这个有歧义的，把"联合"理解成同时适配两个分布。
那么，JDA 方法的目标就是，寻找一个变换 ，使得经过变换后的
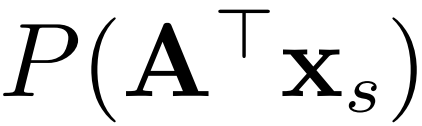和 
的距离能够尽可能地接近，同时，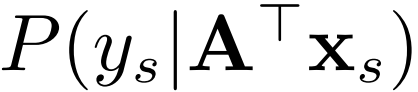
和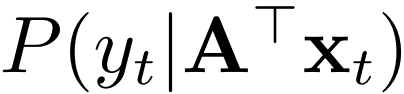 
的距离也要小。很自然地，这个方法也就分成了两个步骤。
2.1 边缘分布适配
首先来适配边缘分布，也就是 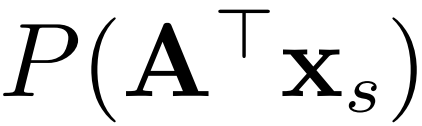和 的距离能够尽可能地接近。其实这个操作就是迁移成分分析 (TCA)。我们仍然使用 MMD 距离来最小化源域和目标域的最 大均值差异。MMD 距离是：
这个式子实在不好求解。我们引入核方法，化简这个式子，它就变成了：
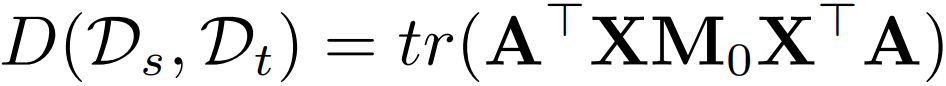
其中 就是变换矩阵，我们把它加黑加粗，
是源域和目标域合并起来的数据。
是一个 MMD 矩阵：
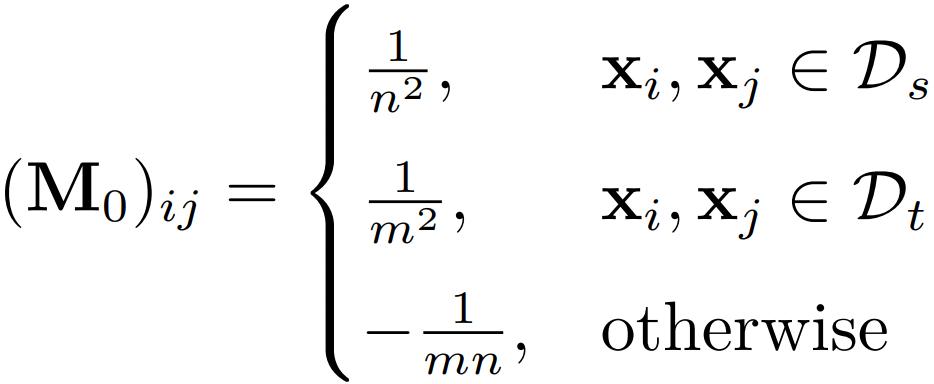
分别是源域和目标域样本的个数。
到此为止没有什么创新点，因为这就是一个 TCA。
2.2 条件分布适配
JDA 迭代算法流程图
这是我们要做的第二个目标，适配源域和目标域的条件概率分布。也就是说，还是要找一个变换 ，使得
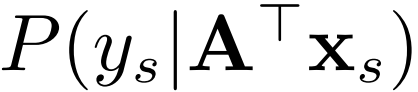和 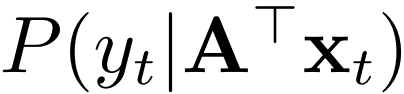的距离也要小。那么简单了，我们再用一遍 MMD 啊。可是问题来了：我们的目标域里，没有 ，没法求目标域的条件分布！
这条路看来是走不通了。也就是说，直接建模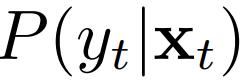 
不行。那么，能不能有别的办法可以逼近这个条件概率？我们可以换个角度，利用类条件概率 
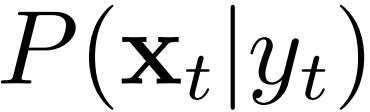。根据贝叶斯公式 
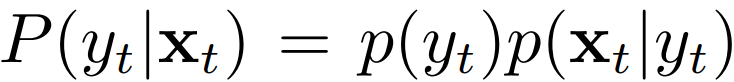，我们如果忽略 
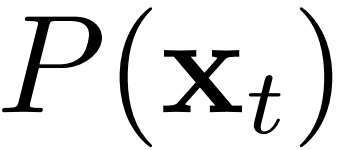，那么岂不是就可以用 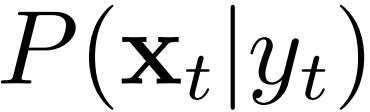来近似？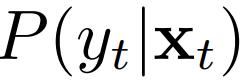
而这样的近似也不是空穴来风。在统计学上，有一个概念叫做充分统计量，它是什么意思呢？大概意思就是说，如果样本里有太多的东西未知，样本足够好，我们就能够从中选择一些统计量，近似地代替我们要估计的分布。好了，我们为近似找到了理论依据。
实际怎么做呢？我们依然没有 yt。采用的方法是，用 (xs, ys) 来训练一个简单的分类器 (比如 knn、逻辑斯特回归)，到 xt 上直接进行预测。总能够得到一些伪标签 yˆt。我们根据伪标签来计算，这个问题就可解了。
类与类之间的 MMD 距离表示为：
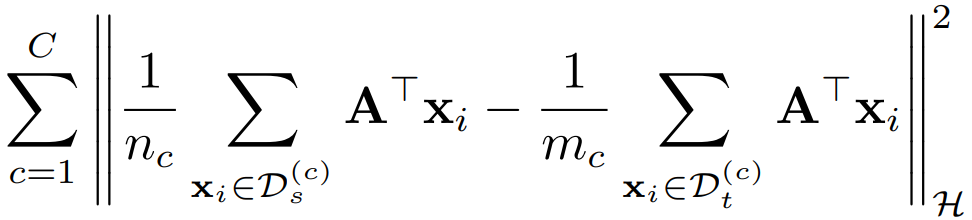
其中， 分别标识源域和目标域中来自第
类的样本个数。同样地我们用核方法， 得到了下面的式子：
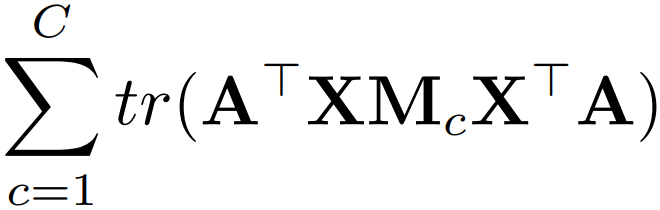
其中 为：
现在我们把两个距离结合起来，得到了一个总的优化目标：
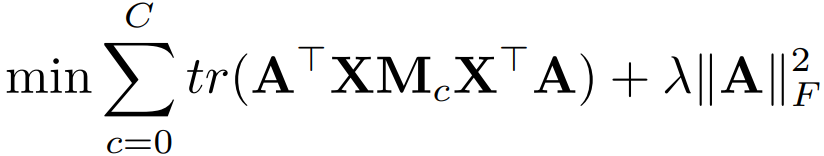
看到没，通过 就把两个距离统一起来了！其中的
是正则项，使得模 型是良好定义 (Well-defined) 的。 我们还缺一个限制条件，不然这个问题无法解。限制条件是什么呢？和 TCA 一样，变 换前后数据的方差要维持不变。怎么求数据的方差呢，还和 TCA 一样：，其中的
也是中心矩阵，
是单位矩阵。也就是说，我们又添加了一个优化目标是要
(这一个步骤等价于 PCA 了)。和原来的优化目标合并，优化目标统一为：
这个式子实在不好求解。但是，有个东西叫做 Rayleigh quotient 1，上面两个一样的这 种形式。因为 是可以进行拉伸而不改改变最终结果的，而如果下面为 0 的话，整个式子 就求不出来值了。所以，我们直接就可以让下面不变，只求上面。所以我们最终的优化问题 形式搞成了：
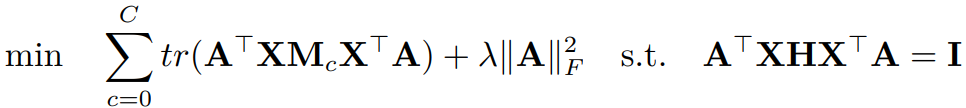
怎么解？太简单了，可以用拉格朗日法。最后变成了：
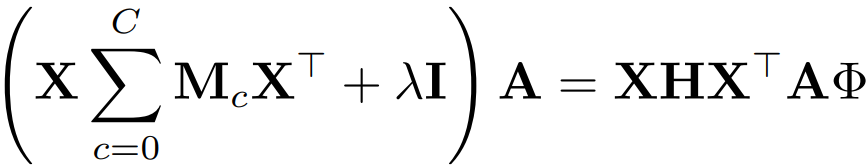
其中的 是拉格朗日乘子。别看这个东西复杂，又有要求解的
，又有一个新加入的
。但是它在 Matlab 里是可以直接解的 (用 eigs 函数即可)。这样我们就得到了变换
，问 题解决了。
可是伪标签终究是伪标签啊，肯定精度不高，怎么办？有个东西叫做迭代，一次不行， 我们再做一次。后一次做的时候，我们用上一轮得到的标签来作伪标签。这样的目的是得到 越来越好的伪标签，而参与迁移的数据是不会变的。这样往返多次，结果就自然而然好了。
2.3 TCA 与 JDA 的比较
我们用一个更直观的可视化结果来初步对比 TCA 与 JDA 的分布效果。
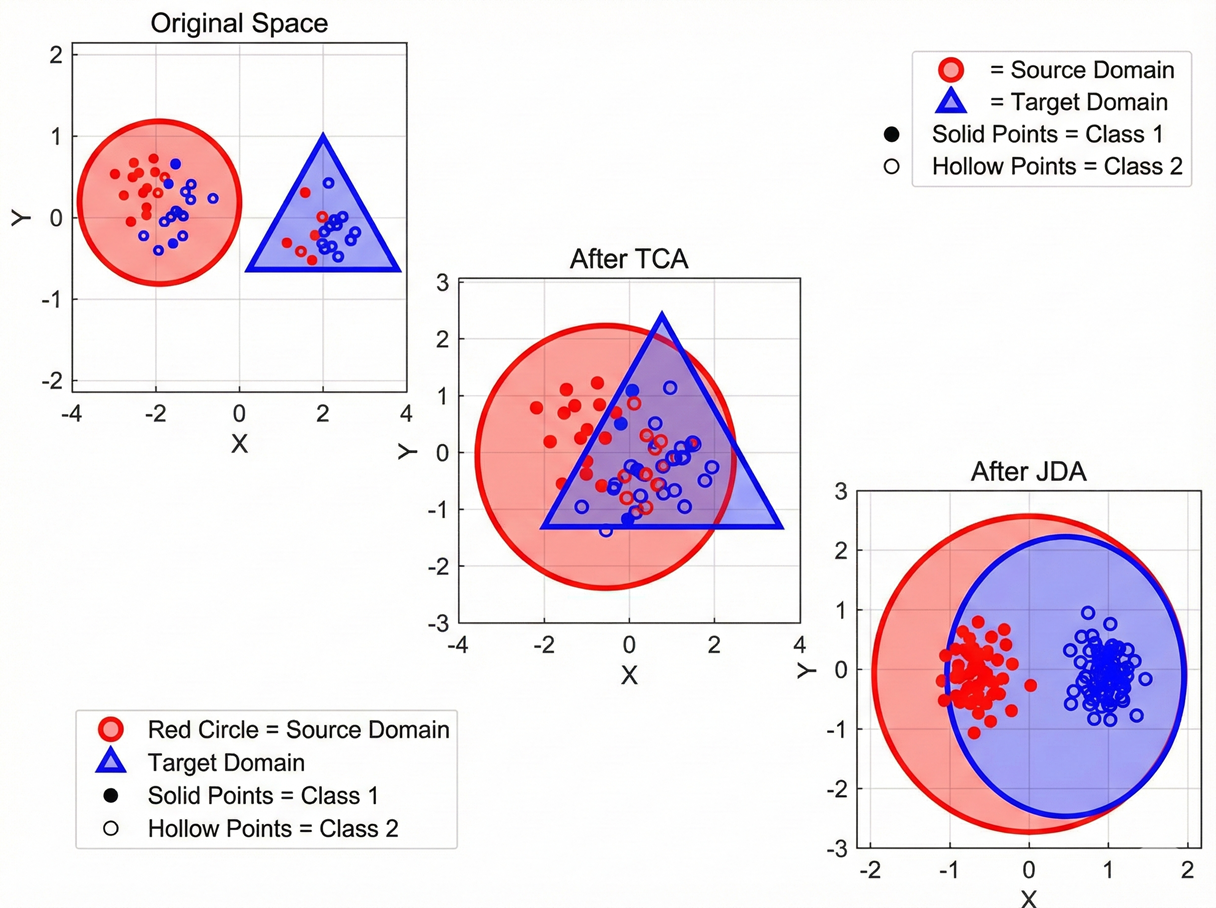TCA 与 JDA 的可视化效果对比
三、参考资料
1. 王晋东《迁移学习简明手册》(PDF版) https://www.labxing.com/files/lab_publications/615-1533737180-LiEa0mQe.pdf#page=82&zoom=100,120,392
2. 《迁移学习简明手册》发布啦！ https://zhuanlan.zhihu.com/p/35352154