文章目录
- 📖1.位运算
-
- [1.1 二进制求和](#1.1 二进制求和)
- [1.2 颠倒二进制位](#1.2 颠倒二进制位)
- [1.3 位1的个数](#1.3 位1的个数)
- [1.4 只出现一次的数字](#1.4 只出现一次的数字)
- [1.5 只出现一次的数字II](#1.5 只出现一次的数字II)
- 🖊️2.
📖1.位运算
1.1 二进制求和

cpp
/*
11
1
-----
100
直接从最后一位开始加,记得算完要翻转
!!最后的时候需要看一下进位,如果有进位的话,还需要补一位
*/
class Solution {
public:
string addBinary(string a, string b) {
int jin = 0;
string ans = "";
for(int i = a.size()-1,j=b.size()-1; i>=0||j>=0; i--,j--){
int cur = jin;
if(i >= 0) cur += a[i] - '0';//字母转数字
if(j >= 0) cur += b[j] - '0';
ans += (cur%2 + '0'); //数字转字母
jin = cur/2;
}
if(jin) ans += '1'; //这里需要注意
reverse(ans.begin(),ans.end());
return ans;
}
};1.2 颠倒二进制位
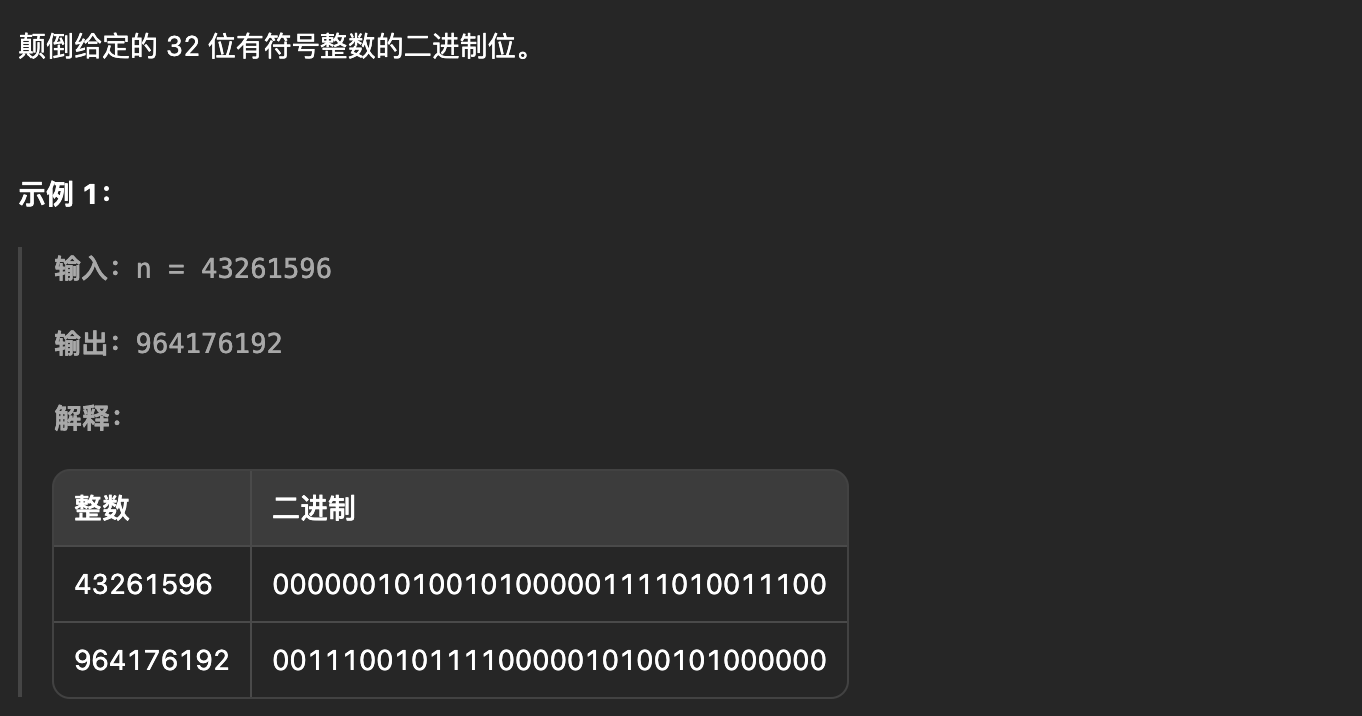

cpp
/*
法1:模拟过程
先获得二进制表达,然后再转为十进制
*/
class Solution {
public:
int reverseBits(int n) {
// string str(32, '1');
string binary = "";
for(int i = 31; i >= 0; i--){
int cur = n%2;
binary+=(cur+'0');
n = n/2;
}
//上面获得的二进制就是反的
int ans = 0;
long long num = 1;
for(int i = 31; i>=0; i--){
ans = ans + (binary[i]-'0')*num;
num *= 2;
}
return ans;
}
};法2:位运算的性质
cpp
// 法2:位运算
class Solution {
public:
int reverseBits(int n) {
int ans = 0;
for(int i = 0; i < 32 && n > 0; i++){
//获得最右边的然后移到左边
ans |= (n & 1) << (31-i);
n>>=1;
}
return ans;
}
};法3:分治(想不到☁️)
cpp
// 法2:位运算
// 时间复杂度:O(logn)。
// 空间复杂度:O(1)。
/*
uint32_t 是无符号的,它 没有负数,因此它的 范围更大,因为没有一位用来表示符号。
32 位 uint32_t 的取值范围是:0 ~ 4,294,967,295(2^32 - 1)
int: -2^31)~ 2,147,483,647(2^31 - 1) /-2,147,483,648 ~
*/
class Solution {
public:
int M1 = 0x55555555; // 01010101010101010101010101010101
int M2 = 0x33333333; // 00110011001100110011001100110011
int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111
int M8 = 0x00ff00ff; // 00000000111111110000000011111111
int reverseBits(long long n) {
n = n >> 1 & M1 | (n & M1) << 1;
n = n >> 2 & M2 | (n & M2) << 2;
n = n >> 4 & M4 | (n & M4) << 4;
n = n >> 8 & M8 | (n & M8) << 8;
return n >> 16 | n << 16;
}
};1.3 位1的个数
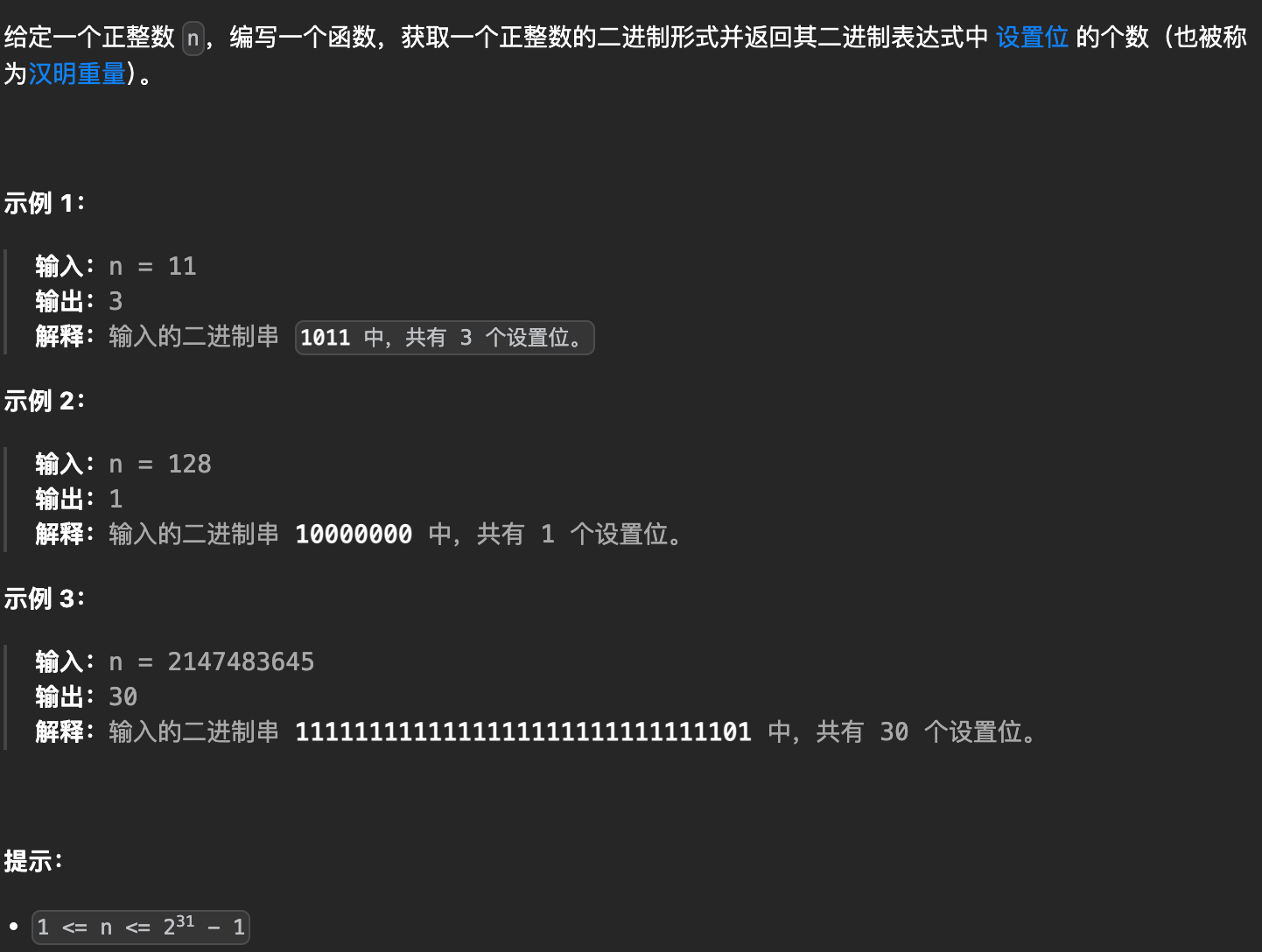
小技巧:
获取最后一个1:int last_one = n & -n;
清除 整数 n 中 最低位的 1,并且 保留其他位不变: n & (n - 1);
12; // 二进制:1100
获取最后一个1: 输出 4(二进制:0100)
只保留最后一个1: 输出 8(二进制:1000)
cpp
/*
位运算判断每一位
*/
class Solution {
public:
int hammingWeight(int n) {
int ans = 0;
while(n != 0){
ans += (n&1)?1:0; //最后一位是1就加1
// if(cur == 1) ans++;
n = n >> 1; //右移1位
}
return ans;
}
};法2:位运算优化
cpp
/*
时间复杂度:O(logn)。循环次数等于 n 的二进制位中 1 的个数
n &(n-1):清除n中最低位的1
位运算判断每一位
*/
class Solution {
public:
int hammingWeight(int n) {
int ans = 0;
while(n != 0){
n = n &(n-1);
ans++;
}
return ans;
}
};1.4 只出现一次的数字

法1:位运算^
cpp
/*
法1:位运算^:相同的为0,最后即为单个的数
时间复杂度:o(N)
*/
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans = nums[0];
for(int i = 1; i < nums.size();i++){
ans ^= nums[i];
}
return ans;
}
};1.5 只出现一次的数字II

cpp
/*
法1:哈希表
时间复杂度:O(n)
空间复杂度:O(n) [n/3+1] 空间复杂度不满足o(1)
*/
class Solution {
public:
int singleNumber(vector<int>& nums) {
unordered_map<int, int> mp;
for(int num: nums){
mp[num]++;
}
int ans = 0;
for (auto it = mp.begin(); it != mp.end(); ++it) {
if(it->second == 1){
ans = it->first;
}
}
return ans;
}
};