人工智能之核心基础机器学习第十章降维算法

人工智能之核心基础机器学习

第十章降维算法

文章目录

[人工智能之核心基础机器学习](#人工智能之核心基础机器学习)

[10.1 降维的目的与意义](#10.1 降维的目的与意义)

[🎯 为什么需要降维？](#🎯 为什么需要降维？)

[🔑 降维的四大价值](#🔑 降维的四大价值)

[10.2 主成分分析（PCA）------最经典的线性降维](#10.2 主成分分析（PCA）——最经典的线性降维)

[🧠 核心思想：找"信息最多的方向"](#🧠 核心思想：找“信息最多的方向”)

[🔍 举个二维例子：](#🔍 举个二维例子：)

[📐 PCA 计算步骤（简化版）](#📐 PCA 计算步骤（简化版）)

[🧪 PCA 代码实现](#🧪 PCA 代码实现)

[🖼️ 案例：用PCA重建图像（理解信息损失）](#🖼️ 案例：用PCA重建图像（理解信息损失）)

[10.3 其他降维算法入门](#10.3 其他降维算法入门)

[1️⃣ t-SNE（t-Distributed Stochastic Neighbor Embedding）](#1️⃣ t-SNE（t-Distributed Stochastic Neighbor Embedding）)

[2️⃣ LDA（Linear Discriminant Analysis）------监督式降维](#2️⃣ LDA（Linear Discriminant Analysis）——监督式降维)

[🧪 t-SNE vs PCA 可视化对比](#🧪 t-SNE vs PCA 可视化对比)

[10.4 实战案例](#10.4 实战案例)

[案例1：PCA 用于人脸识别预处理](#案例1：PCA 用于人脸识别预处理)

[案例2：t-SNE 展示高维数据分布（鸢尾花）](#案例2：t-SNE 展示高维数据分布（鸢尾花）)

[🎯 本章总结：降维算法选择指南](#🎯 本章总结：降维算法选择指南)

资料关注

10.1 降维的目的与意义

🎯 为什么需要降维？

想象你有一张1000万像素的照片 ，但手机屏幕只有200万像素 。

你不需要所有细节，只需保留"看起来像"的关键信息------这就是降维！

✅ 核心目标 ：用更少的特征 ，保留最重要的信息

🔑 降维的四大价值

目的	说明	实际好处
减少特征维度	从1000维 → 10维	模型训练更快、内存占用更小
降低计算成本	减少矩阵运算量	适合部署到手机/边缘设备
去除噪声和冗余	过滤无用或重复信息	提升模型泛化能力，防过拟合
可视化高维数据	把数据降到2D/3D	直观观察聚类、分布、异常点

💡 经典场景：

人脸识别：64×64=4096维 → 50维主成分

文本分析：词典10万词 → TF-IDF 1000维 → PCA 50维

基因数据：2万个基因表达 → 降维后聚类找疾病亚型

10.2 主成分分析（PCA）------最经典的线性降维

🧠 核心思想：找"信息最多的方向"

PCA 不是随机删特征，而是旋转坐标轴 ，找到数据变化最大的方向作为新坐标。

✅ 最大方差理论 ：

方差越大，说明数据在这个方向上越"分散"，包含的信息越多！

🔍 举个二维例子：

原始数据在 x 和 y 轴都有分布，但其实主要沿一条斜线变化。

PCA 会找到这条主方向 （第一主成分），再找与之垂直的次方向（第二主成分）。

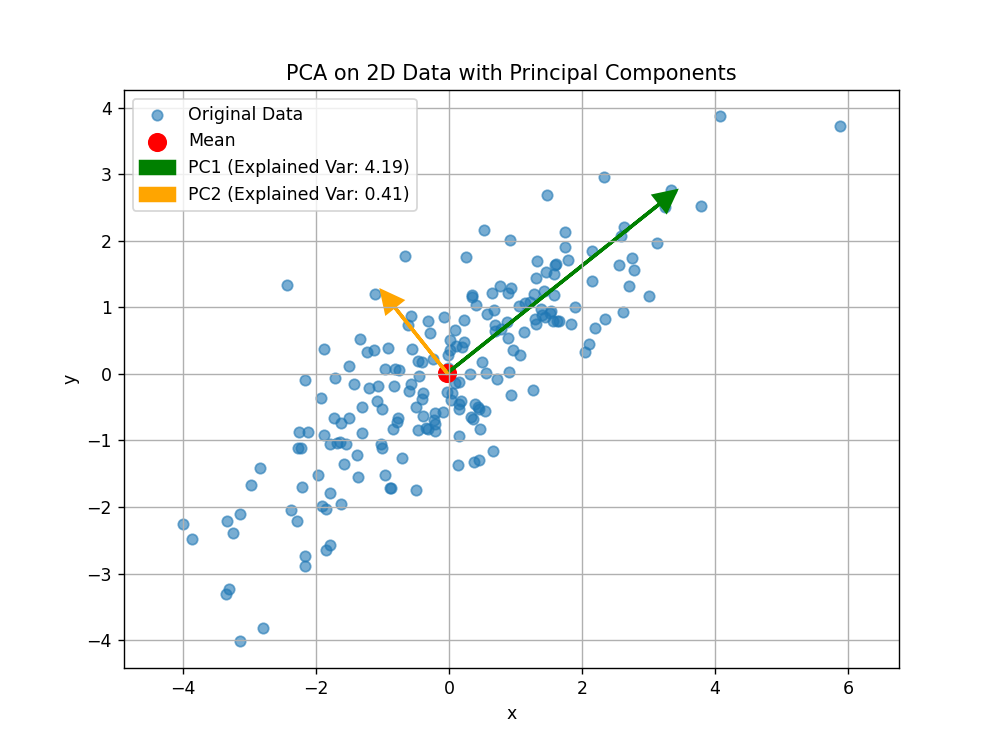
图：第一主成分（PC1）捕捉了最大方差

📐 PCA 计算步骤（简化版）

标准化数据 （均值为0，方差为1） ⚠️ 必须做！否则量纲大的特征主导结果
计算协方差矩阵（衡量特征间相关性）
求特征值 & 特征向量
- 特征值大小 = 该方向的方差（信息量）
- 特征向量 = 主成分方向
选择前 k 个最大特征值对应的特征向量
将原始数据投影到新空间

📌 关键参数 ：n_components

可指定数量（如 n_components=2）

也可指定保留方差比例（如 n_components=0.95 → 保留95%信息）

🧪 PCA 代码实现

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits, make_classification
from sklearn.preprocessing import StandardScaler

# 加载手写数字数据（8x8=64维）
digits = load_digits()
X, y = digits.data, digits.target

# 标准化（PCA强烈建议！）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# PCA 降到2维用于可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 可视化
plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='tab10', alpha=0.6)
plt.colorbar(scatter)
plt.title(f"PCA 降维 (保留方差: {pca.explained_variance_ratio_.sum():.2%})")
plt.xlabel("第一主成分")
plt.ylabel("第二主成分")
plt.show()

# 查看各主成分解释的方差比例
print("前5个主成分解释方差比例:", pca.explained_variance_ratio_[:5])

🖼️ 案例：用PCA重建图像（理解信息损失）

python 复制代码

# 尝试不同维度重建数字"8"
digit_8 = X[0].reshape(8, 8)

# 不同主成分数
n_comps = [2, 10, 30, 64]
fig, axes = plt.subplots(1, len(n_comps)+1, figsize=(12, 3))

# 原图
axes[0].imshow(digit_8, cmap='gray')
axes[0].set_title("原始图像")
axes[0].axis('off')

for i, n in enumerate(n_comps):
    pca_temp = PCA(n_components=n)
    X_trans = pca_temp.fit_transform(X_scaled)
    X_recon = pca_temp.inverse_transform(X_trans)  # 重建
    
    recon_img = X_recon[0].reshape(8, 8)
    axes[i+1].imshow(recon_img, cmap='gray')
    axes[i+1].set_title(f"{n}维\n(保留{pca_temp.explained_variance_ratio_.sum():.0%})")
    axes[i+1].axis('off')

plt.tight_layout()
plt.show()

💡 观察：即使只用10个主成分（≈60%方差），数字仍可辨认！

10.3 其他降维算法入门

1️⃣ t-SNE（t-Distributed Stochastic Neighbor Embedding）

目的：高维数据可视化（几乎只用于2D/3D）
核心思想 ：保持局部相似性
- 高维中相近的点 → 低维中也相近
- 高维中远离的点 → 低维中可远可近
特点：
- 非线性、非确定性（每次结果略有不同）
- 不能用于新数据（无 transform 接口）
- 对超参敏感（perplexity 关键）

✅ 适用：MNIST、人脸、单细胞RNA-seq等复杂结构可视化

2️⃣ LDA（Linear Discriminant Analysis）------监督式降维

前提：有标签 ！属于监督学习
目标：找到能最大化类间距离、最小化类内距离的投影方向
限制：最多降到 (类别数 - 1) 维
- 二分类 → 最多1维
- 10类 → 最多9维

✅ 适用：分类前的特征压缩（如人脸识别）

🧪 t-SNE vs PCA 可视化对比

python 复制代码

from sklearn.manifold import TSNE

# t-SNE 降维（较慢！）
tsne = TSNE(n_components=2, perplexity=30, random_state=42, n_iter=1000)
X_tsne = tsne.fit_transform(X_scaled)

# 对比图
fig, ax = plt.subplots(1, 2, figsize=(14, 5))

ax[0].scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='tab10', alpha=0.6)
ax[0].set_title("PCA")

ax[1].scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='tab10', alpha=0.6)
ax[1].set_title("t-SNE")

plt.show()

🔍 观察：

PCA：全局结构保留，但类别可能重叠

t-SNE：同类聚集紧密，不同类分离清晰（更适合可视化聚类效果）

10.4 实战案例

案例1：PCA 用于人脸识别预处理

python 复制代码

from sklearn.datasets import fetch_olivetti_faces

# 加载人脸数据（400张，64x64）
faces = fetch_olivetti_faces()
X_face, y_face = faces.data, faces.target

# PCA 降到100维（原4096维）
pca_face = PCA(n_components=100, whiten=True)  # whitening提升效果
X_face_pca = pca_face.fit_transform(X_face)

print(f"压缩率: {X_face_pca.shape[1] / X_face.shape[1]:.2%}")
print(f"保留方差: {pca_face.explained_variance_ratio_.sum():.2%}")

# 可视化前5个"特征脸"（eigenfaces）
fig, axes = plt.subplots(1, 5, figsize=(10, 3))
for i in range(5):
    eigenface = pca_face.components_[i].reshape(64, 64)
    axes[i].imshow(eigenface, cmap='gray')
    axes[i].set_title(f"主成分 {i+1}")
    axes[i].axis('off')
plt.suptitle("特征脸（PCA主成分）")
plt.show()

💡 "特征脸"是人脸的基本构成单元，类似"五官模板"

案例2：t-SNE 展示高维数据分布（鸢尾花）

python 复制代码

from sklearn.datasets import load_iris

iris = load_iris()
X_iris, y_iris = iris.data, iris.target

# t-SNE 降维
tsne_iris = TSNE(n_components=2, random_state=42)
X_iris_tsne = tsne_iris.fit_transform(X_iris)

plt.scatter(X_iris_tsne[:, 0], X_iris_tsne[:, 1], c=y_iris, cmap='Set1', s=80)
plt.title("鸢尾花 t-SNE 可视化")
plt.show()

🎯 本章总结：降维算法选择指南

算法	类型	是否需标签	用途	优点	缺点
PCA	线性	❌ 无监督	通用降维、去噪、加速	快、可逆、保留全局结构	无法捕捉非线性关系
t-SNE	非线性	❌ 无监督	可视化	聚类效果惊艳	慢、不可逆、不能用于新数据
LDA	线性	✅ 监督	分类前降维	利用标签信息，提升分类效果	维度受限（≤C-1）

💡 实践建议：

先用 PCA：快速降维、去噪、加速后续模型

再用 t-SNE：仅用于最终结果可视化（别用于训练！）

如果有标签且做分类：试试 LDA（尤其小样本）

资料关注

公众号：咚咚王

《Python编程：从入门到实践》

《利用Python进行数据分析》

《算法导论中文第三版》

《概率论与数理统计（第四版） (盛骤) 》

《程序员的数学》

《线性代数应该这样学第3版》

《微积分和数学分析引论》

《（西瓜书）周志华-机器学习》

《TensorFlow机器学习实战指南》

《Sklearn与TensorFlow机器学习实用指南》

《模式识别（第四版）》

《深度学习 deep learning》伊恩·古德费洛著花书

《Python深度学习第二版(中文版)【纯文本】 (登封大数据 (Francois Choliet)) (Z-Library)》

《深入浅出神经网络与深度学习+(迈克尔·尼尔森（Michael+Nielsen）》

《自然语言处理综论第2版》

《Natural-Language-Processing-with-PyTorch》

《计算机视觉-算法与应用(中文版)》

《Learning OpenCV 4》

《AIGC：智能创作时代》杜雨+&+张孜铭

《AIGC原理与实践：零基础学大语言模型、扩散模型和多模态模型》

《从零构建大语言模型（中文版）》

《实战AI大模型》

《AI 3.0》

人工智能之核心基础 机器学习 第十章 降维算法