统计学基础与数据可视化实战——基本图表（1）

一、核心概念：数据的"集中趋势"与"离散程度"

在分析任何一组数据（比如100根薯条的长度）时，我们通常关心两个最核心的问题：

集中趋势：这批数据的"平均水平"大概在哪里？（平均数、中位数、众数）
离散程度：这批数据是整齐划一，还是长短不一？（方差、标准差）

理解了这个框架，我们再来看每个具体的指标。

二、详解五大指标：从"薯条长度"说起

1. 平均数

它是什么：最常说的"平均"。把所有数值加起来，然后除以数量。
怎么算：(第1根长度 + 第2根长度 + ... + 第100根长度) ÷ 100
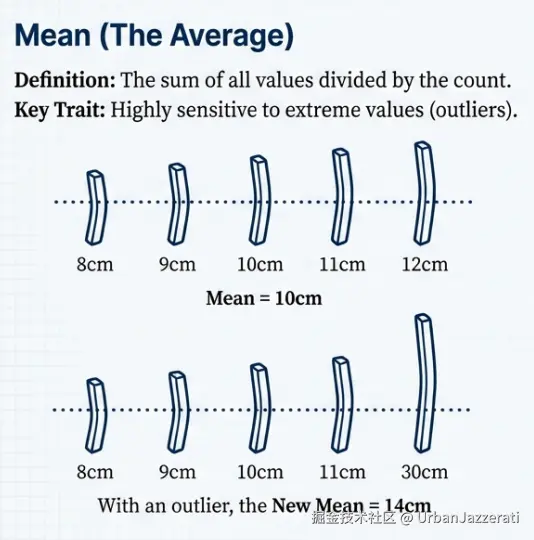
薯条例子 ：5根薯条长度分别是 8cm, 9cm, 10cm, 11cm, 12cm。平均数 = (8+9+10+11+12) / 5 = 10cm。
实际应用：
- 计算班级平均分：了解班级整体学习水平。
- 计算家庭月平均开销：规划家庭预算。
注意：平均数对极端值非常敏感。如果5根薯条中有一根是30cm长的"巨无霸"薯条，平均数就会被拉高到14cm，无法代表大多数薯条的真实长度。

2. 中位数

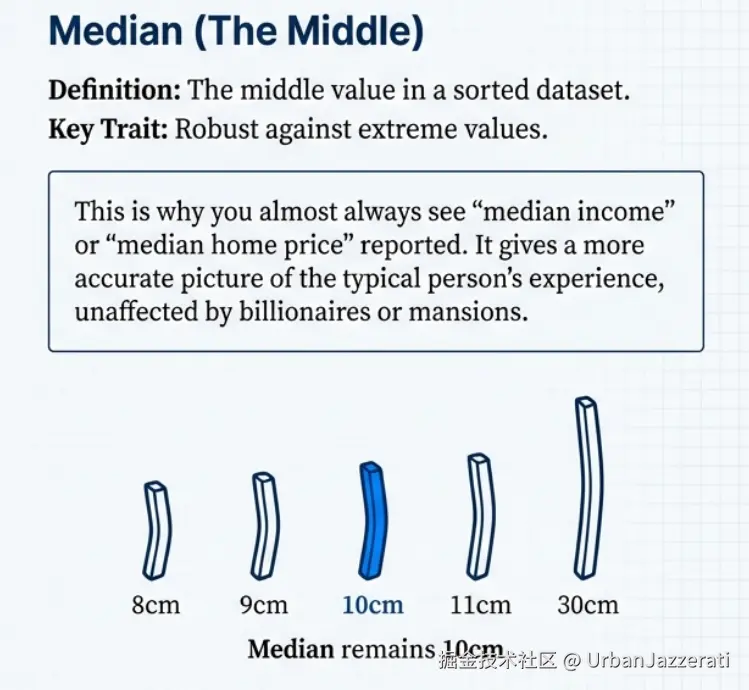
它是什么 ：将数据从小到大排序 后，正中间的那个数。它能避免被极端值影响。
怎么找：先排序，找中间位置。
薯条例子：
- 同样5根薯条：8, 9, 10 , 11, 12 → 中位数是 10cm。
- 加入"巨无霸"薯条：8, 9, 10, 11, 30 → 中位数依然是 10cm。看，它不受影响！
实际应用：
- 了解"普通水平" ：比如国家或城市居民收入中位数，比平均收入更能反映普通人的真实收入情况，因为不会被少数富豪的收入拉高。
- 寻找中心趋势：在房价、薪资等可能包含极高或极低值的数据中，中位数比平均数更有参考价值。

3. 众数

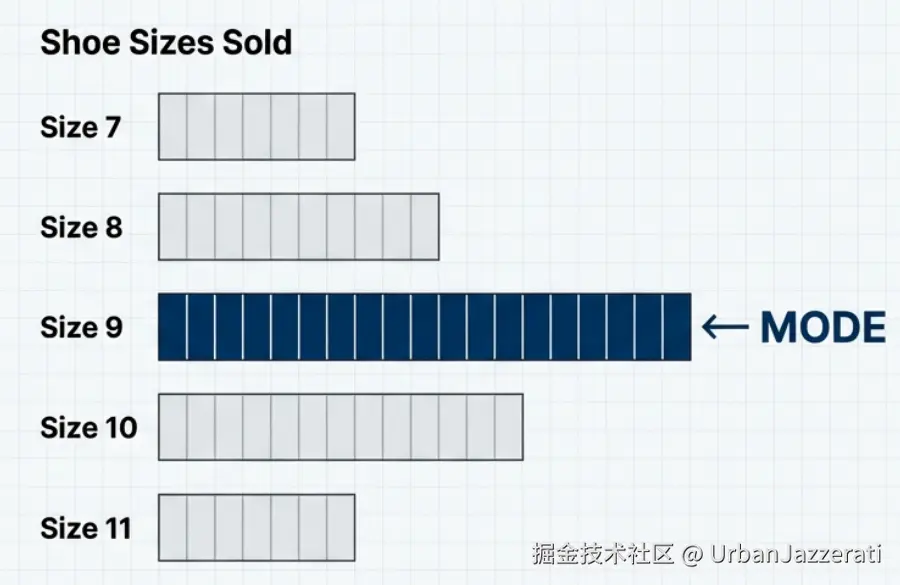
它是什么 ：一组数据中，出现次数最多的那个数值。
怎么找：统计哪个数字出现得最频繁。
薯条例子 ：又一批7根薯条长度：8, 9, 10, 10, 10, 11, 12。长度"10cm"出现了3次，最多 → 众数是 10cm。
实际应用：
- 了解"最常见"的情况 ：服装鞋帽店根据众数（卖得最多的尺码）来进货，而不是根据平均尺码。
- 市场调研：调查消费者最喜欢的手机颜色，结果"黑色"被选择最多，"黑色"就是众数。

4. 方差

它是什么 ：衡量数据波动大小 或分散程度 的一个指标。计算的是每个数据点与平均数差距的平方的平均值。
为什么平方？为了避免差值有正有负，相加时相互抵消（比如比平均长3cm和短3cm，直接加是0，无法体现波动）。平方能让所有差值都变成正数，放大波动的影响。
薯条例子：有两批薯条，平均数都是10cm。
- A批：9, 10, 11 （很均匀）
- B批：5, 10, 15 （长短不一）
  计算它们与平均数(10)的差值平方的平均：
- A批方差：[(9-10)² + (10-10)² + (11-10)²] / 3 = (1+0+1)/3 ≈ 0.67
- B批方差：[(5-10)² + (10-10)² + (15-10)²] / 3 = (25+0+25)/3 ≈ 16.67
  B批的方差远大于A批，说明B批薯条长度差异更大，质量不稳定。
主要用途 ：在数学上便于计算和推导，是统计学中的重要基础概念。

5. 标准差

它是什么 ：方差的平方根。目的是把方差"平方化"的单位，变回和原始数据一样的单位，让我们能直观地理解波动的实际大小。
薯条例子：接上面的方差。
- A批标准差 = √0.67 ≈ 0.82 cm
- B批标准差 = √16.67 ≈ 4.08 cm
  现在我们可以直观地说：A批薯条的长度大多在 10cm ± 0.82cm 之间波动，很稳定；B批则在 10cm ± 4.08cm 之间波动，质量很差。
实际应用（极其重要） ：
- 产品质量控制：工厂设定标准，规定零件尺寸的标准差必须小于0.1mm，以确保所有产品几乎一样。
- 投资风险衡量 ：股票或基金净值的标准差越大，代表其价格波动越剧烈，风险越高。
- 考试成绩分析：一次考试的标准差大，说明学生成绩两极分化严重。

三、一张图看懂区别与应用

指标	关注点	通俗理解	生活应用场景	受极端值影响
平均数	总体平均水平	"算出来的平均"	计算平均成绩、平均工资	非常大
中位数	中间位置水平	"排出来的中间"	衡量居民典型收入、房价中位数	几乎没有
众数	最常见的情况	"数出来的最多"	确定最畅销的服装尺码、最常见的意见	几乎没有
方差	数据波动程度	"波动大小的平方值"	主要用于统计学理论计算	大
标准差	数据波动程度	"波动大小的实际值"	产品质量控制、金融风险衡量	大

四、综合实战：分析一次考试成绩

假设某次艰难的数学考试，全班10人成绩为：35, 50, 65, 70, 75, 78, 80, 85, 90, 100（最后一位是学霸）。

平均数 = 约 73分。但这个"平均"被学霸的100分拉高了，可能让老师误以为大家考得还行。
中位数 = 排序后第5、6位的平均：(75+78)/2 = 76.5分。这个数更能代表班里"中间梯队"的水平。
众数：没有重复分数，所以无众数。如果大多数人考了70分，那么众数70分就很有意义。
方差 & 标准差 ：计算后会得到较大的值（因为35分和100分差距巨大）。这告诉老师：这次考试成绩分布非常分散，学生水平差距极大，可能需要分层辅导。

总结与记忆口诀

想知总体平均水平，用 平均数（小心极端值骗你）。
想找典型不受干扰，用 中位数（收入房价常用它）。
想看哪个最多最火，用 众数（市场调查要靠它）。
想晓数据稳不稳定，看 标准差（质量控制、风险衡量都找它）。
方差 是 标准差 的数学爸爸，理论计算离不开它。

核心原则：一张图看懂如何选择

在深入细节前，记住这个最根本的选图逻辑：

比较大小 → 条形图
看趋势变化 → 线形图（折线图）
看占比关系 → 饼图/环形图
吸引眼球、简单比较 → 象形统计图

下面我们逐一详解。

五. 象形统计图：让数据"活"起来

它是什么 ：用小图标（象形符号）的数量或大小来代表数据多少的图表。它更像是"数据插图"，追求直观和视觉冲击力。
最佳使用场景：
- 面向公众或儿童的科普、宣传材料。
- 需要快速、直观地传达数量对比，且数据项较少时。
- 例如：比较两个品牌的销量、展示不同能源的发电量。
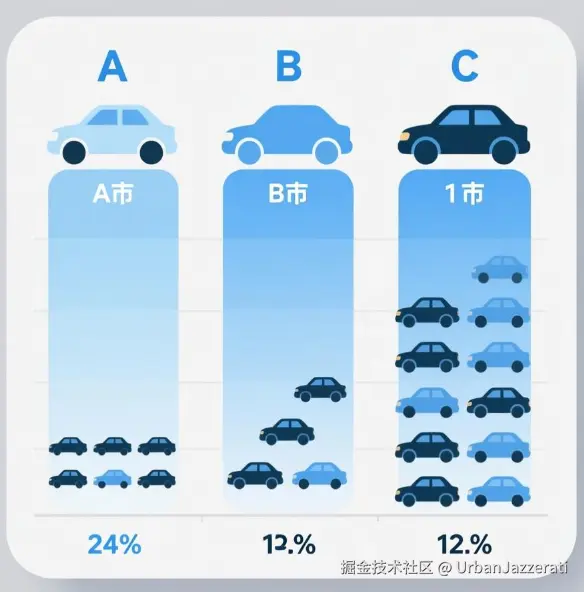
一个例子：比较A、B、C三个城市的汽车保有量。
- 图表描述：用三辆小汽车图标排成三行，A城市下面有8辆车，B城市下面有5辆车，C城市下面有12辆车。一眼就能看出C城市最多。

✅ 最佳实践与⚠️注意事项：
- 优点：非常直观、吸引人，即使不认识字也能看懂。
- 缺点：不精确，难以表达复杂数据和细微差别。
- 重要原则：
  1. 一个图标必须代表固定的数量（比如1个房子图标 = 1000套住房）。忌用图标大小不同来比较（人眼对面积不敏感）。
  2. 数据复杂或需要精确阅读时，避免使用。

六. 条形图：比较冠军

它是什么 ：用一系列高度或长度与数据值成比例的矩形（柱子）来表示数据大小的图表。有纵向（柱状图）和横向（条形图）两种。
最佳使用场景：
- 比较不同类别之间的数值大小（例如：比较不同产品的销量、不同国家的人口）。
- 显示一段时间内的数据，但类别数量较少或类别名称较长时（例如：比较2023年各季度的营收）。
- 横向条形图特别适合类别名称很长的情况，方便阅读。
一个例子：2023年公司各产品线销售额。
- 图表描述：横轴是产品名称（手机、电脑、平板、耳机），纵轴是销售额。电脑的柱子最高，耳机的最矮，清晰展示谁卖得最好。
✅ 最佳实践与⚠️注意事项：
- 柱子必须等宽，间距一致。
- 纵轴必须从0开始！否则会严重误导观众，夸大差异。
- 对柱子进行排序（从高到低或从低到高），能让比较更容易。
- 使用颜色可以高亮重点数据（如将销量第一的产品柱子标成特殊颜色）。

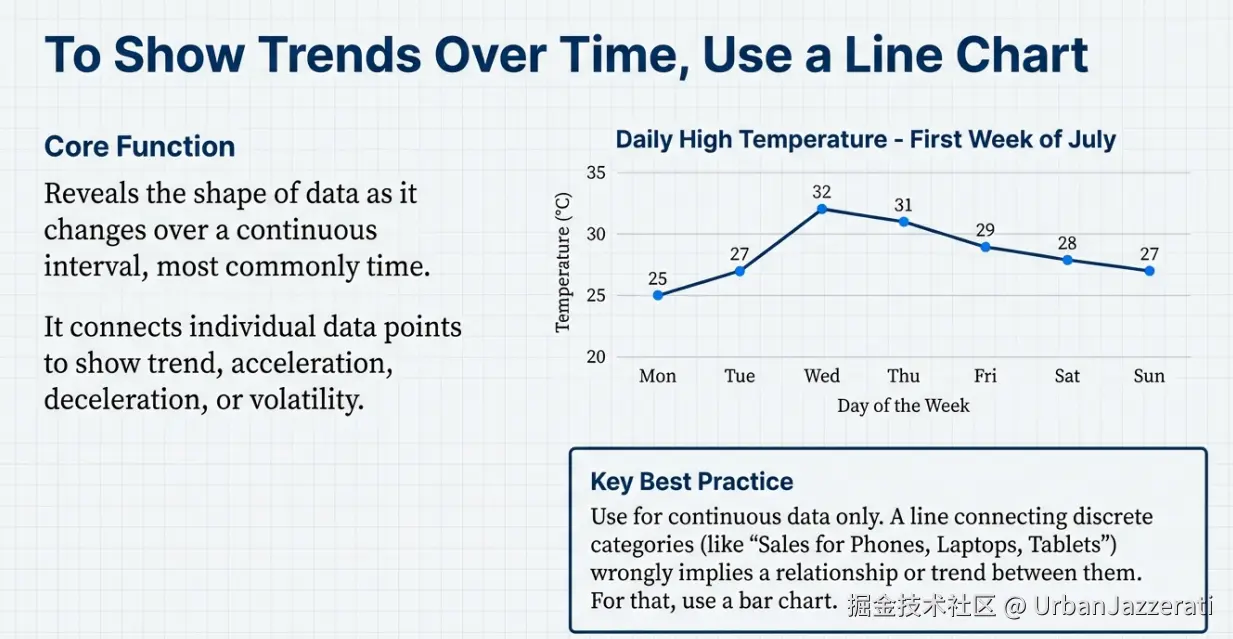
七. 线形图：看见趋势

它是什么 ：将一系列连续的数据点用直线连接起来 的图表，主要用于显示数据随时间或其他连续变量而变化的趋势。
最佳使用场景：
- 展示数据在连续区间（尤其是时间）上的变化趋势（例如：公司股价每日波动、一年中的气温变化、网站月度访问量）。
- 比较多个数据系列在同一时期的趋势（例如：比较A、B两款产品在过去一年的销量趋势线）。
一个例子：某城市过去一周的日最高气温变化。
- 图表描述：横轴是日期（周一到周日），纵轴是温度（摄氏度）。将每天的温度点连成线，可以看到周三最高，周末有所下降的"先升后降"趋势。
✅ 最佳实践与⚠️注意事项：
- 横轴必须是连续的（如时间、距离），不能是"产品A、产品B"这类离散类别。
- 线条不宜过多，同时比较的线条最好不超过4-5条，否则会像一团乱麻。
- 可以搭配数据标记点（圆圈、方块）来突出具体的数据值。
- 如果纵轴差距很大，可以使用双纵轴来比较不同量级的数据（需谨慎，并明确标注）。

八. 饼图：展示"蛋糕"怎么分

它是什么 ：一个被分割成若干扇形的圆，每个扇形的面积（圆心角大小） 代表该部分在总体中所占的百分比。
最佳使用场景：
- 展示一个整体（100%）被分割成几个部分时，各部分的占比关系。
- 强调某一部分在整体中的重要程度（例如：展示公司最大营收来源的占比）。
- 仅用于显示静态的构成比例，不适用于随时间变化的数据。
一个例子：公司本月市场费用预算构成。
- 图表描述：一个完整的圆饼，其中数字广告占45%（最大的一块），线下活动占30%，内容制作占20%，其他占5%。一眼可知主要花费在数字广告上。
✅ 最佳实践与⚠️注意事项：
- 扇形部分最好不超过6个，否则会难以阅读。可以将众多小份额合并为"其他"项。
- 务必标注百分比或具体数值，因为人眼不擅长精确比较角度大小。
- 从12点钟方向开始，按份额从大到小顺时针排列，看起来最舒服。
- 避免使用3D效果或爆炸式饼图，它们会扭曲视觉判断。
- 当需要比较多个"整体"的构成时，不要用多个饼图 ，改用堆叠百分比条形图会更清晰。

总结：四大基础图表速查手册

为了让你一目了然，我将这四种图表的核心特性、适用场景和要点总结在下表中：

特性图表类型	核心功能	最佳使用场景	关键注意事项
象形统计图	直观展示、视觉吸引	公众宣传、儿童教育、简单数量对比	1个图标=固定数量；避免用于精确或复杂数据
条形图	精确比较各类别数值大小	比较产品销量、国家人口、季度营收等	纵轴从0开始；可对类别排序；适合名称长的类别用横向
线形图	揭示数据随时间的变化趋势	股价波动、气温变化、访问量趋势、多系列趋势对比	横轴需连续（如时间）；同时显示线条不宜过多
饼图	展示整体中各部分的占比关系	预算构成、市场份额、选民支持率等静态比例	部分数≤6 ；标注百分比；避免用于趋势比较

最终决策指南：我该用什么图？

最后，让我们通过一个具体的场景来串联所有知识。假设你是某品牌的市场分析师，手头有去年的销售数据，你需要向老板汇报：

"老板，我想看看咱们哪款产品卖得最好？"
- 👉 用条形图。把各产品名称放在横轴，销量作为柱子高度，高低立判。
"老板，我想看看咱们旗舰产品全年的销售走势，有没有季节性规律？"
- 👉 用线形图。把12个月份放在横轴，每月销量连成线，上升下降趋势一目了然。
"老板，我想看看咱们的钱都花在哪些渠道了，大头在哪？"
- 👉 用饼图。清晰地展示广告、促销、研发等各项费用占总预算的百分比。
"老板，我们要做一张给消费者看的宣传海报，想突出我们用户数量是竞争对手的两倍！"
- 👉 用象形统计图。画两排小人图标，我们品牌下面小人图标数量是对手的两倍，视觉冲击力强，易懂。

记住，图表是为你讲故事的工具。选择那个能让你的数据故事讲得最清晰、最有力的工具。先从掌握这四种基础图表开始，你就能解决工作中80%以上的数据展示需求了。

一个中性的"诚实"图表

假设某公司过去12个月的营收（单位：万元）如下：
[100, 101, 102, 103, 104, 105, 106, 108, 110, 112, 115, 118]

事实：营收在稳定、缓慢地增长，从100万到118万，全年增长约18%。

现在，我们来看看如何"改造"这个图表。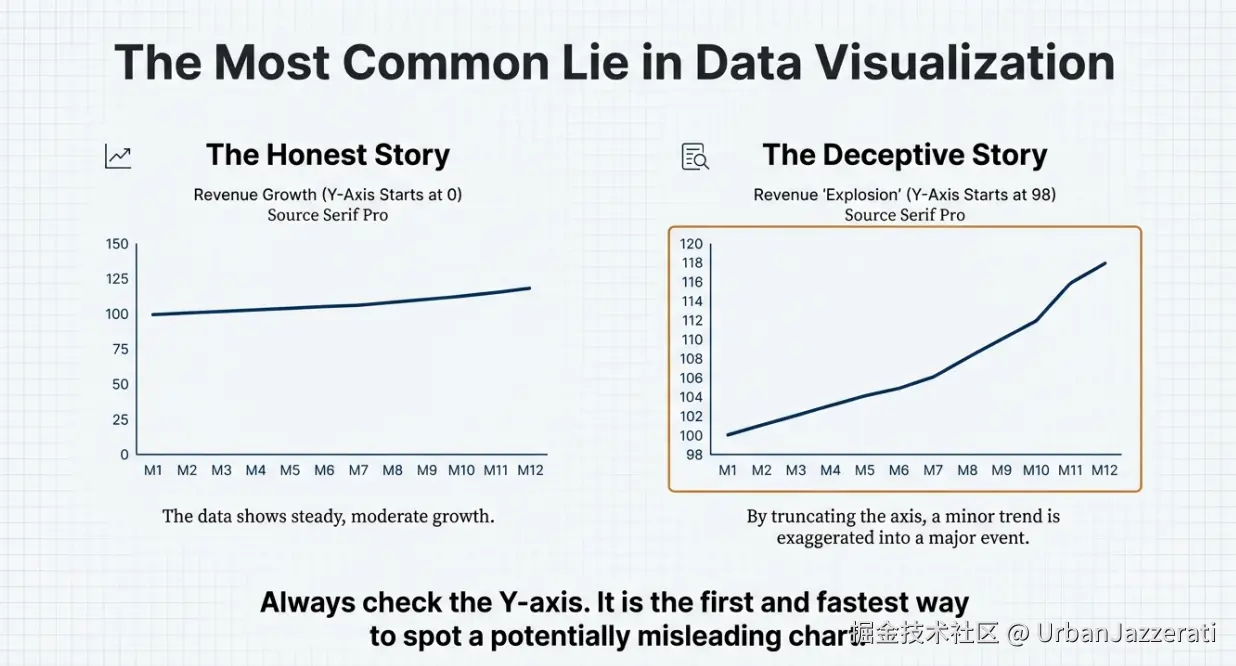

误导手法一：截断Y轴（最常见、最狡猾）

操作方法 ：不让纵轴从0开始，而是从一个接近数据最小值的数字开始（比如从98开始）。
误导效果：微小的绝对变化（18个单位），在视觉上被放大成巨大的相对波动，让平缓的增长看起来像"飙升"或"暴跌"。
对比：左边诚实的图表显示增长平缓；右边误导的图表显示增长陡峭，像业绩"火箭式上升"。
如何识破 ：第一眼永远看纵轴起点！ 检查坐标轴是否从0开始。商业新闻、广告中尤其常见。

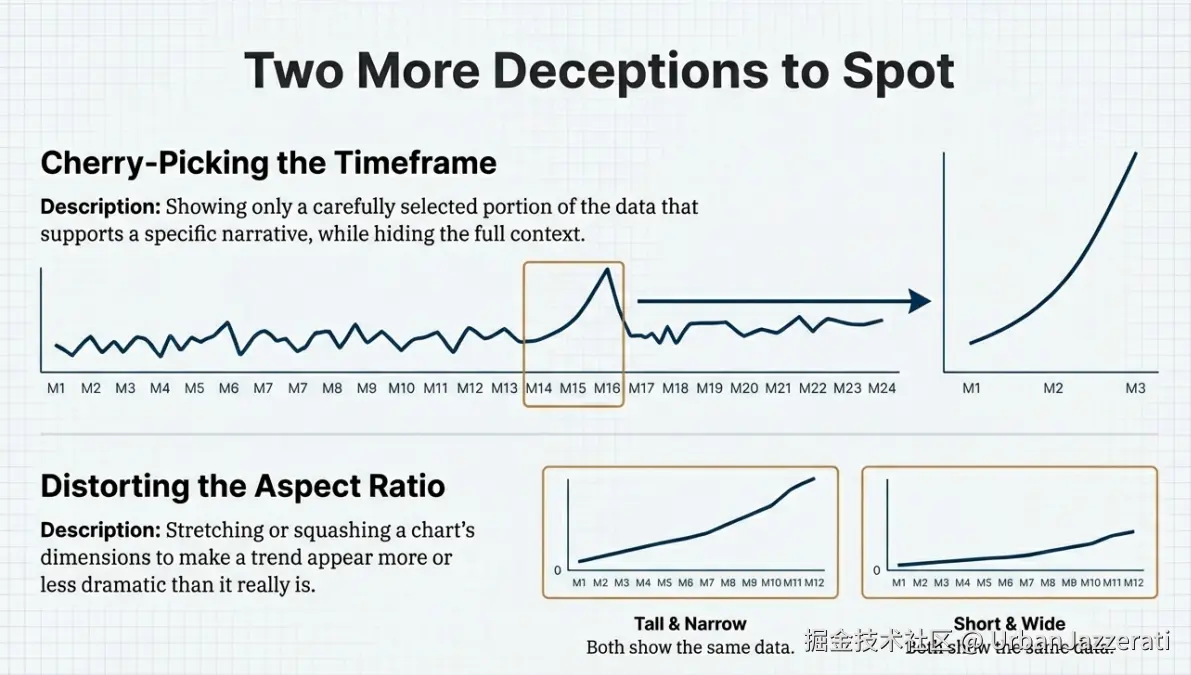
误导手法二：扭曲比例（压缩或拉伸）

操作方法 ：人为调整图表的 "长宽比" 。横轴被拉得很长，或纵轴被压得很扁。
误导效果：
- 横轴过长：趋势看起来更平缓，掩盖变化。（"看，我们的业绩一直很稳定！"）
- 纵轴过长/横轴过短：趋势看起来更剧烈，夸大波动。（"看，我们的增长势头多猛！"）
如何识破：关注图表整体的"坡度"。同一个数据，在不同形状的图表里，会讲出完全不同的故事。

误导手法三：选择性呈现数据（断章取义）

操作方法 ：只展示对论点有利的时间段，隐藏不利的数据。
例子：只展示上面数据中最后3个月 [112, 115, 118]。
误导效果："本公司最近一季度营收强劲增长！"------这是事实，但它隐藏了全年增长平缓的整体背景。如果选取1月、6月、12月三个点，甚至可以连出一条更陡的直线。
如何识破 ：质疑时间范围。"为什么从这时开始？到这时结束？" 要求查看更长时间跨度的完整数据。

误导手法四：使用非线性刻度（高阶误导）

操作方法 ：在应该使用线性刻度（均匀间隔）的轴上，使用对数刻度。
对数刻度的正当用途 ：显示跨越多个数量级的数据（比如从1到1,000,000）的增长率（百分比），例如看病毒传播速度、国家GDP长期趋势。
误导效果 ：如果数据量级差异不大（如我们的营收数据），用对数刻度会严重压平趋势，让增长看起来微不足道。
如何识破 ：查看坐标轴标注。线性刻度：0, 50, 100, 150...；对数刻度：1, 10, 100, 1000... 或明确标有"对数刻度"。

其他常见误导手法

连接不应连接的点 ：如果数据点代表独立的、非连续的类别（如"苹果、香蕉、橙子"的销量），用线连起来暗示一种趋势或连续性，这是误导的。线形图只应用于连续数据（如时间序列）。
混淆相关性与因果性：两条趋势线走势相似，就断言"A导致B"。（例如："冰淇淋销量上升时，溺水人数也上升，所以冰淇淋导致溺水？" 实际是两者都受夏天高温影响。）
不标注关键事件：在趋势突然变化时（如骤降），不标注可能的原因（如"主要竞争对手发布新品"），让人无法正确解读数据。

总结：一张"防误导"检查清单

当你看到任何一个线形图时，请养成习惯，快速核对以下问题：

检查项	诚实图表特征	误导性警报
1. 纵轴起点	通常从0开始	纵轴被截断，起点远大于0
2. 坐标轴刻度	刻度均匀（线性）	使用对数刻度但未明确告知或理由不充分
3. 图表长宽比	比例适中，坡度自然	图形被异常压扁或拉高，导致趋势失真
4. 数据完整性	展示了合理、完整的时间段	时间段选择可疑，可能隐藏了重要前期/后期数据
5. 数据连续性	数据点代表连续变量（如时间）	用线连接了独立不连续的类别数据
6. 因果断言	谨慎描述"伴随发生"的趋势	仅凭曲线相似就声称"导致"

核心心法 ：线形图的核心是展示趋势。任何让趋势的视觉斜率发生非数据本身改变的操作，都可能是误导。

给你的建议 ：作为读者，保持批判性思维，永远多看两眼坐标轴。作为制作者，坚守诚信，纵轴从0开始是黄金准则（除非有极特殊的正当理由并明确标注），选择合理的时间范围，让你的数据真实地自我表达。

理解这些后，你不仅能识破大多数数据诡计，也能做出更专业、更令人信服的图表。