计算机视觉入门到实战系列（八）Harris角点检测算法

_codemonster2026-01-11 11:54

Harris角点检测算法

Harris角点检测是一种经典的角点检测算法，用于检测图像中亮度变化明显的角点（corners）。

角点的定义：在两个垂直方向上都有明显灰度变化的点。

三种图像区域类型：

  1. 平坦区域 - 所有方向灰度变化都小
  2. 边缘区域 - 一个方向变化大，垂直方向变化小
  3. 角点区域 - 所有方向灰度变化都大

原理

  1. 灰度变化度量
    对于图像窗口平移 ( u , v ) (u,v) (u,v)，灰度变化 E ( u , v ) E(u,v) E(u,v)：
    E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u,v) = \sum_{x,y} w(x,y)[I(x+u,y+v) - I(x,y)]^2 E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
  • I ( x , y ) I(x,y) I(x,y)：像素点 ( x , y ) (x,y) (x,y)的灰度值
  • w ( x , y ) w(x,y) w(x,y)：窗口函数（通常为高斯权重）
  1. 泰勒展开近似
    使用泰勒展开：
    I ( x + u , y + v ) ≈ I ( x , y ) + u I x + v I y I(x+u,y+v) \approx I(x,y) + uI_x + vI_y I(x+u,y+v)≈I(x,y)+uIx+vIy
    其中 I x = ∂ I ∂ x I_x = \frac{\partial I}{\partial x} Ix=∂x∂I， I y = ∂ I ∂ y I_y = \frac{\partial I}{\partial y} Iy=∂y∂I

代入得：
E ( u , v ) ≈ ∑ w ( x , y ) [ u 2 I x 2 + 2 u v I x I y + v 2 I y 2 ] E(u,v) \approx \sum w(x,y)[u^2I_x^2 + 2uvI_xI_y + v^2I_y^2] E(u,v)≈∑w(x,y)[u2Ix2+2uvIxIy+v2Iy2]

  1. 结构张量M
    E ( u , v ) ≈ [ u v ] M [ u v ] E(u,v) \approx [u \ v] M \begin{bmatrix} u \\ v \end{bmatrix} E(u,v)≈[u v]M[uv]

    其中：
    M = ∑ w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] M = \sum w(x,y) \begin{bmatrix} I_x^2 & I_xI_y \\ I_xI_y & I_y^2 \end{bmatrix} M=∑w(x,y)[Ix2IxIyIxIyIy2]

  2. Harris响应函数

    设 λ 1 \lambda_1 λ1和 λ 2 \lambda_2 λ2是矩阵 M M M的特征值：

  • 平坦区域： λ 1 ≈ λ 2 ≈ 0 \lambda_1 \approx \lambda_2 \approx 0 λ1≈λ2≈0
  • 边缘区域： λ 1 ≫ λ 2 ≈ 0 \lambda_1 \gg \lambda_2 \approx 0 λ1≫λ2≈0 或 λ 2 ≫ λ 1 ≈ 0 \lambda_2 \gg \lambda_1 \approx 0 λ2≫λ1≈0
  • 角点区域： λ 1 \lambda_1 λ1和 λ 2 \lambda_2 λ2都大且相近

定义响应函数：
R = det ⁡ ( M ) − k ⋅ trace ( M ) 2 R = \det(M) - k \cdot \text{trace}(M)^2 R=det(M)−k⋅trace(M)2

或展开为：
R = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2 R = \lambda_1\lambda_2 - k(\lambda_1 + \lambda_2)^2 R=λ1λ2−k(λ1+λ2)2

其中 k k k是经验常数（通常0.04-0.06）

Harris算法就是在每个像素点上问：

"如果我往四周稍微动一动，看到的景象会大变样吗？"

  • 完全不变 → 平坦区域（墙面）

  • 只在一个方向变 → 边缘区域（门框）

  • 往哪动都大变样 → ⭐角点！（窗户角）

代码实现

python 复制代码 
from utils import *


# 计算角点响应函数
def responseFunc(M):
    # 设置超参数
    k = 0.04
    
    # 计算M的行列式
    det = np.linalg.det(M)
    # 计算M的迹
    trace = np.trace(M)
    
    # 计算角点响应函数
    R = det - k * trace ** 2
    
    return R


# Harris角点检测算法
def harris_corners(src, NMS=False):
    
    # 获得输入图像的长宽
    h, w = src.shape[:2]
    
    # 将图像转为灰度图像
    gray_image = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
    
    # 初始化角点矩阵
    cornerPoint = np.zeros_like(gray_image,dtype=np.float32)
    
    # 计算图像沿横轴和纵轴的梯度
    grad = np.zeros((h, w, 2), dtype=np.float32)
    # x轴梯度
    grad[:,:,0] = cv2.Sobel(gray_image, cv2.CV_16S, 1, 0)
    # y轴梯度
    grad[:,:,1] = cv2.Sobel(gray_image, cv2.CV_16S, 0, 1)
    
    # 计算黑塞矩阵内元素的值，此时的值是求和的结果，即M矩阵的元素
    Ixx = grad[:,:,0] ** 2
    Iyy = grad[:,:,1] ** 2
    Ixy = grad[:,:,0] * grad[:,:,1]
     
    # 计算窗口内黑塞矩阵元素的值，窗函数使用高斯函数
    Ixx = cv2.GaussianBlur(Ixx, (3, 3), sigmaX=2)
    Iyy = cv2.GaussianBlur(Iyy, (3, 3), sigmaX=2)
    Ixy = cv2.GaussianBlur(Ixy, (3, 3), sigmaX=2)
    
    for i in range(gray_image.shape[0]):
        for j in range(gray_image.shape[1]):
            
            # 构建M矩阵
            struture_matrix = [[Ixx[i][j], Ixy[i][j]], 
                               [Ixy[i][j], Iyy[i][j]]]

            # 计算角点响应函数
            R = responseFunc(struture_matrix)
            cornerPoint[i][j] = R

    # 非最大抑制
    corners = np.zeros_like(gray_image, dtype=np.float32)
    threshold = 0.01
    
    # 返回所有角点响应的最大值
    maxValue = np.max(cornerPoint)
    
    # 我们将角点响应函数的阈值设定为 threshold * maxValue
    
    for i in range(cornerPoint.shape[0]):
        for j in range(cornerPoint.shape[1]):
            
            # 如果进行NMS操作
            if NMS:
                # 当前角点响应值大于阈值，同时也是邻居周围的最大值
                if cornerPoint[i][j] > threshold * maxValue and \
                    cornerPoint[i][j] == np.max(
                    cornerPoint[max(0, i - 1):min(i + 1, h - 1), 
                    max(0, j - 1):min(j + 1, w - 1)]):
                    
                    corners[i][j] = 255
            else:
                # 当前角点响应值大于阈值
                if cornerPoint[i][j] > threshold * maxValue:
                    corners[i][j] = 255
                    
    # 返回检测到的角点
    return corners

输入彩色图像 → 灰度化 → 计算梯度 → 计算结构张量M → 高斯加权 → 计算角点响应R → 阈值处理 → (可选)NMS → 输出角点图

1. 整体结构

代码包含两个主要函数：

  • responseFunc()：计算角点响应函数R
  • harris_corners()：主函数，执行完整的Harris角点检测流程

2. responseFunc() 函数

python 复制代码 
def responseFunc(M):
    k = 0.04  # 经验常数，通常取0.04-0.06
    det = np.linalg.det(M)      # 计算M的行列式
    trace = np.trace(M)         # 计算M的迹
    R = det - k * trace ** 2    # Harris响应函数
  • 目的：根据结构张量M计算角点响应值R
  • 数学原理 ：
    • 平坦区域：两个特征值都很小，R≈0
    • 边缘区域：一个特征值大，一个特征值小，R<0
    • 角点区域：两个特征值都很大，R>0

3. harris_corners() 函数

3.1 预处理阶段

python 复制代码 
# 转为灰度图（因为角点检测基于梯度）
gray_image = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)

# 初始化角点矩阵
cornerPoint = np.zeros_like(gray_image, dtype=np.float32)

3.2 梯度计算

python 复制代码 
# 使用Sobel算子计算x和y方向梯度
grad[:,:,0] = cv2.Sobel(gray_image, cv2.CV_16S, 1, 0)  # Ix
grad[:,:,1] = cv2.Sobel(gray_image, cv2.CV_16S, 0, 1)  # Iy

# 计算结构张量M的元素
Ixx = grad[:,:,0] ** 2   # Ix²
Iyy = grad[:,:,1] ** 2   # Iy²
Ixy = grad[:,:,0] * grad[:,:,1]  # IxIy

3.3 窗口加权（高斯滤波）

python 复制代码 
# 使用3×3高斯核平滑，sigma=2
Ixx = cv2.GaussianBlur(Ixx, (3, 3), sigmaX=2)
Iyy = cv2.GaussianBlur(Iyy, (3, 3), sigmaX=2)
Ixy = cv2.GaussianBlur(Ixy, (3, 3), sigmaX=2)
  • 作用：对梯度乘积进行加权平均，考虑局部邻域信息
  • 使用高斯窗口而非矩形窗口，离中心越近权重越大

3.4 构建结构张量并计算响应

python 复制代码 
for i in range(gray_image.shape[0]):
    for j in range(gray_image.shape[1]):
        # 构建2×2结构张量M
        struture_matrix = [[Ixx[i][j], Ixy[i][j]], 
                          [Ixy[i][j], Iyy[i][j]]]
        
        # 计算每个像素的角点响应
        R = responseFunc(struture_matrix)
        cornerPoint[i][j] = R

3.5 阈值处理与非极大值抑制（NMS）

python 复制代码 
# 自适应阈值：最大响应的1%
threshold = 0.01
maxValue = np.max(cornerPoint)

if NMS:  # 使用非极大值抑制
    # 检查是否为局部极大值（3×3邻域）
    if cornerPoint[i][j] > threshold * maxValue and \
        cornerPoint[i][j] == np.max(
        cornerPoint[max(0, i-1):min(i+1, h-1), 
                   max(0, j-1):min(j+1, w-1)]):
        corners[i][j] = 255  # 标记为角点
else:    # 不使用NMS
    if cornerPoint[i][j] > threshold * maxValue:
        corners[i][j] = 255
  • k=0.04：经验常数，控制边缘抑制程度
  • sigmaX=2：高斯核标准差，控制窗口大小
  • threshold=0.01：响应阈值比例因子

5. 输出

函数返回一个二值图像corners，其中255表示检测到的角点位置。

函数调用

默认NMS为False

python 复制代码 
# 图像素材来自opencvpython网站
img = cv2.imread('sudoku.png')

plt.imshow(img[:, :, ::-1])
plt.axis('off')
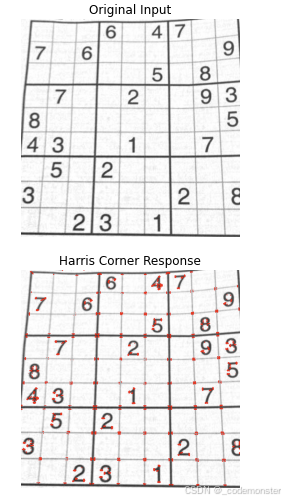
plt.title('Original Input')
plt.show()

response = harris_corners(img)
img[response == 255] = [0, 0, 255]
plt.imshow(img[:, :, ::-1])
plt.axis('off')
plt.title('Harris Corner Response')
plt.show()

这行代码的作用是：在原图img上将所有检测到的角点位置标记为红色。

python 复制代码 
img[response == 255] = [0, 0, 255]
  • response == 255：创建一个布尔掩码（boolean mask），其中：
    • True：表示response矩阵中值等于255的位置（即检测到的角点）
    • False：表示其他位置
  • img[response == 255]：使用布尔索引选择img中所有角点位置的像素
  • [0, 0, 255]：BGR格式的红色（OpenCV使用BGR而非RGB）
    • B=0, G=0, R=255 → 纯红色

启用NMS

python 复制代码 
# 图像素材来自opencvpython网站
img = cv2.imread('sudoku.png')

plt.imshow(img[:, :, ::-1])
plt.axis('off')
plt.title('Original Input')
plt.show()

response = harris_corners(img,NMS=True)
img[response == 255] = [0, 0, 255]
plt.imshow(img[:, :, ::-1])
plt.axis('off')
plt.title('Harris Corner Response')
plt.show()

输出

相关推荐
Snow_day.9 小时前
有关排列排列组合（1）
数据结构·算法·贪心算法·动态规划·图论
默默前行的虫虫9 小时前
nicegui的3D可视化
python
hui函数9 小时前
Python系列Bug修复｜如何解决 pip install -e . 安装报错 “后端不支持可编辑安装（PEP 660）” 问题
python·bug·pip
dora9 小时前
【开发火星地平线辅助】智商不够，编程来凑
算法
二哈喇子！9 小时前
PyTorch与昇腾平台算子适配：从注册到部署的完整指南
人工智能·pytorch·python
im_AMBER9 小时前
Leetcode 100 在链表中插入最大公约数
数据结构·c++·笔记·学习·算法·leetcode·链表
FPGAI9 小时前
Python之函数
开发语言·python
Z1Jxxx9 小时前
删除字符串2
开发语言·c++·算法
踩坑记录9 小时前
leetcode hot100 15. 三数之和 medium
算法·leetcode·职场和发展
热门推荐
01GitHub 镜像站点02Labelme从安装到标注：零基础完整指南03Linux下V2Ray安装配置指南04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05jdk21下载、安装（Windows、Linux、macOS）06Claude Code 2.1.2 升级报错？别折腾了，一行命令搞定072025-04-03 Latex学习1——本地配置Latex + VScode环境08【踩坑笔记】50系显卡适配的 PyTorch 安装09UV安装并设置国内源10自用Proteus(8.15)常用元器件图示和功能介绍(持续更新...)