机器学习，梯度下降，拟合，正则化，混淆矩阵

小兔崽子去哪了2026-01-11 12:53

梯度下降

什么是梯度下降法

  • 梯度下降过程就和下山场景类似
  • 可微分的损失函数，代表着一座山
  • 寻找的函数的最小值，也就是山底
  • 单变量函数中，梯度就是某一点切线斜率（某一点的导数）；有方向为函数增长最快的方向
  • 多变量函数中，梯度就是某一个点的偏导数；有方向：偏导数分量的向量方向

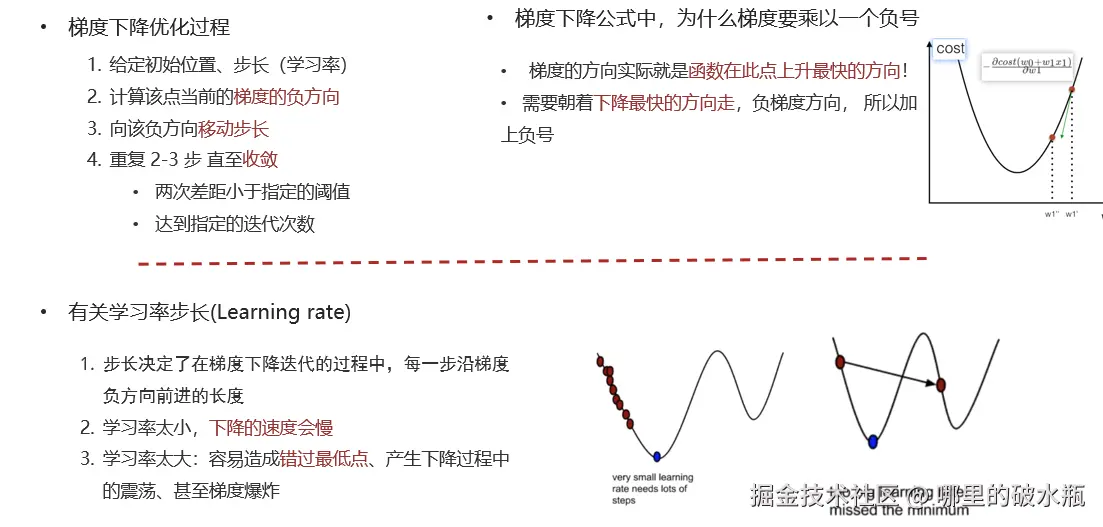
梯度下降公式

  • 循环迭代求当前点的梯度，更新当前的权重参数
  • α: 学习率(步长) 不能太大, 也不能太小. 机器学习中：0.001 ~ 0.01
  • 梯度是上升最快的方向, 我们需要是下降最快的方向, 所以需要加负号

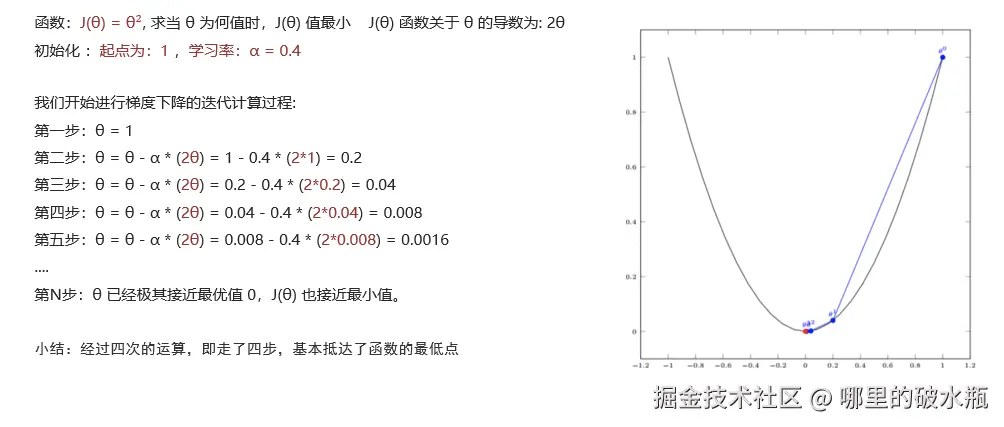
单变量梯度下降

多变量梯度下降

对比

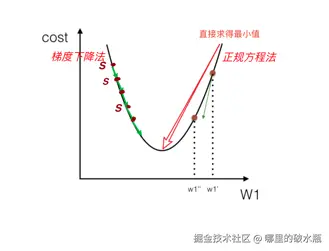
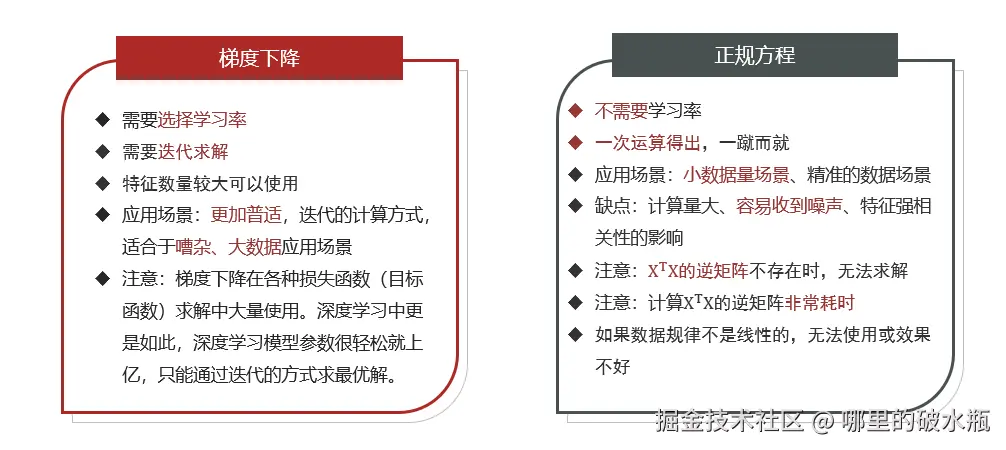
梯度下降法与正规方程对比

模型评估

一般使用 MAE 和 RMSE 这两个指标

MAE平均绝对误差 反应的是真实的平均误差，RMSE均方根误差会将误差大的数据点放大

MAE 不能体现出误差大的数据点，普遍分布。

RMSE放大大误差的数据点对指标的影响，但是对异常数据比较敏感，更好的看异常值情况

结论

  • 都能反映出预测值和真实值之间的误差
  • MAE对误差大小不敏感
  • RMSE会放大预测误差较大的样本的影响
  • RMSE对异常数据敏感

波士顿房价预测

正规方程法 和 梯度下降的区别

相同点：都可以用来找损失函数极小值，评估回归模型

不同点：

  • 正规方程：一次性求解，资源开销极大，适合于小批量干净的数据集，如果数据集没有逆，也无法计算
  • 梯度下降：迭代求解，资源开销相对较小，适用于大批量的数据集，实际开发更推荐。
    • 分类
    • 全梯度下降
    • 随机梯度下降
    • 小批量梯度下降
    • 随机平均梯度下降

评估的方案

  • 方案1：平均绝对误差：Mean Absolute Error，误差绝对值的和的平均值
  • 方案2：均方误差：Mean Squared Error，误差的平方和的平均值
  • 方案3：均方根误差：Root Mean Squared Error，误差的平方和平均值的平方根

机器学习研发流程

  1. 获取数据
  2. 数据预处理
  3. 特征工程
    • 特征提取，特征预处理（标准化，归一化），特征降维，特征选取，特征组合
  4. 模型训练
  5. 模型评估
  6. 模型预测

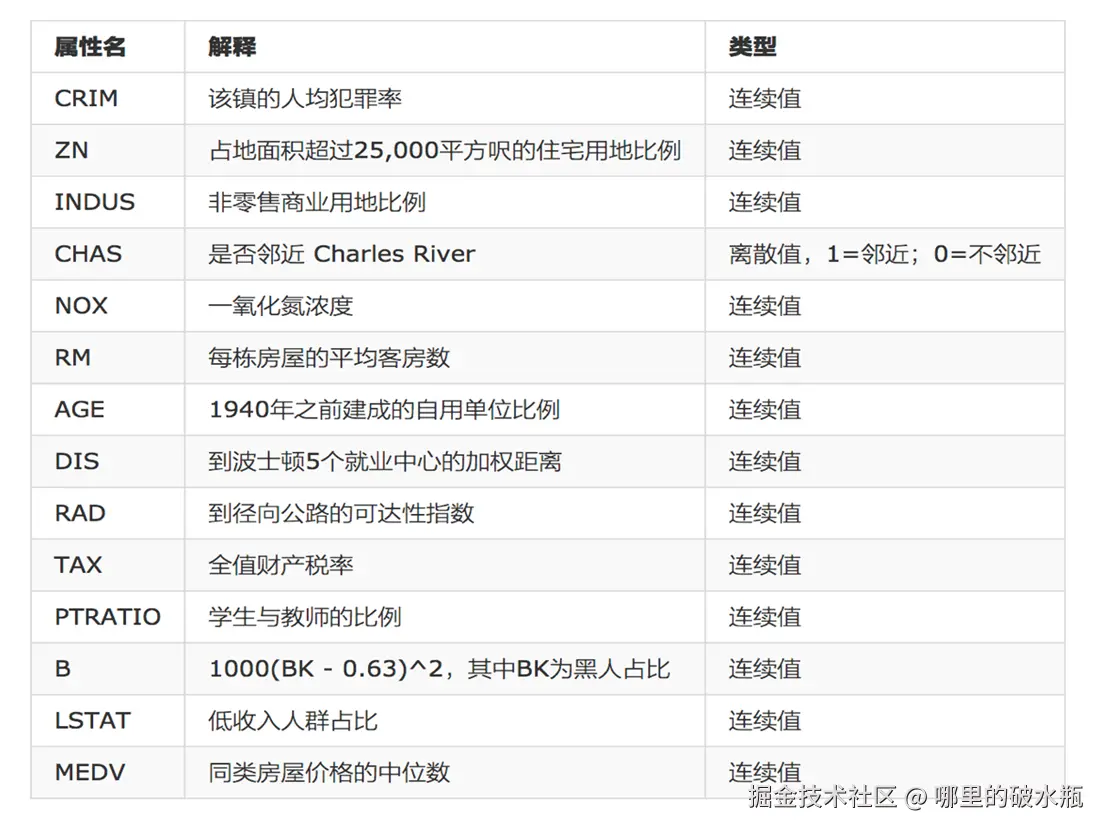
正规方程法

py 复制代码 
import numpy as np
import pandas as pd
from skimage.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, root_mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# TODO: 1. 获取数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
# 数据，特征
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
# 标签
target = raw_df.values[1::2, 2]

print(f'特征：{len(data)}, {data[:5]}')
print(f'标签：{len(target)}, {target[:5]}')

# TODO: 2. 划分数据集
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=22)

# TODO: 3. 特征工程，特征提取，特征预处理(标准化，归一化)，特征降维，特征选取，特征组合
# 创建标准化对象
transfer = StandardScaler()
# 对训练集和测试集进行标准化处理
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# TODO 4. 模型训练
# 创建线性回归之正规方程对象

# fit_intercept 是否考虑偏置（截距）
estimator = LinearRegression(fit_intercept=True)
# 训练
estimator.fit(x_train, y_train)

# TODO 5. 模型预测
y_predict = estimator.predict(x_test)
print(f'预测值：{y_predict}')
print(f'权重：{estimator.coef_}')
print(f'偏置：{estimator.intercept_}')

# TODO 6. 模型评估
# 参数一真实值，参数二预测值
print(f'平均绝对值误差：{mean_absolute_error(y_test, y_predict)}')
print(f'均方误差：{mean_squared_error(y_test, y_predict)}')
print(f'均方根误差：{root_mean_squared_error(y_test, y_predict)}')

梯度下降法

对于小数据集，正规方程的效果会更好。

py 复制代码 
import numpy as np
import pandas as pd
from skimage.metrics import mean_squared_error
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_absolute_error, root_mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

print(f'特征：{len(data)}, {data[:5]}')
print(f'标签：{len(target)}, {target[:5]}')

x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=22)

transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# fit_intercept 是否考虑偏置（截距），参数2： 学习率是常量，参数3：学习率
estimator = SGDRegressor(fit_intercept=True, learning_rate='constant', eta0=0.001)
estimator.fit(x_train, y_train)

y_predict = estimator.predict(x_test)
print(f'预测值：{y_predict}')
print(f'权重：{estimator.coef_}')
print(f'偏置：{estimator.intercept_}')

print(f'平均绝对值误差：{mean_absolute_error(y_test, y_predict)}')
print(f'均方误差：{mean_squared_error(y_test, y_predict)}')
print(f'均方根误差：{root_mean_squared_error(y_test, y_predict)}')

拟合

拟合

指的是模型和数据之间存在关系，即：预测值和真实值之间的关系

欠拟合：模型在训练集，测试集标签都不好，原因是模型过于简单了。

过拟合：模型在训练集表现好，在测试集表现不好，原因是模型过于复杂了，数据不纯，数据量少。

正好拟合(泛化)，模型在训练集，测试集都好。

奥卡姆剃刀：在误差(泛化程度都一样)相同的情况下，优先选择简单的模型。

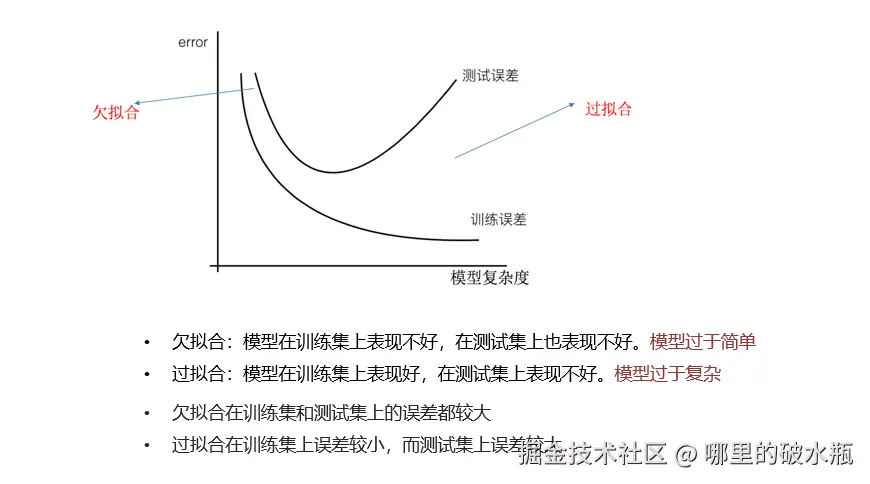
欠拟合

py 复制代码 
import matplotlib.pyplot as plt
import numpy as np
from skimage.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.metrics import root_mean_squared_error, mean_absolute_error

# TODO: 设置随机种子
# 设置随机数种子
np.random.seed(666)

# 生成 x 轴数据，100 个
x = np.random.uniform(-3, 3, size=100)

# TODO: y 这样写，是为了 人为构造一份接近真实世界的数据

# 基于x轴的值，结合线性公式，生成y轴的值
# 问题一线性回归公式：y = kx+b，这里为了数据更好，加入噪声...
# 即：y = 0.5x² + x + 2 + 噪声(正态分布生成的随机数)
# np.random.normal(0, 1, size=100) 的意思是，生成正态分布的随机数，均值为0，标准差为1，大小为100
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

print(f'查看数据x：{x}')
print(f'查看数据集y：{y}')

# TODO：2. 数据预处理
X1 = x.reshape(-1, 1)
print(f'处理后的数据集X：{X1}')

# TODO: 3. 创建模型（算法）对象
estimator = LinearRegression()
estimator.fit(X1, y)

# TODO: 4. 模型预测
y_predict = estimator.predict(X1)

# TODO: 5. 模型评估
print(f'均方误差：{mean_squared_error(y, y_predict)}')
print(f'均方根误差：{root_mean_squared_error(y, y_predict)}')
print(f'平均绝对误差：{mean_absolute_error(y, y_predict)}')

# TODO：6. 绘制图形
plt.scatter(x, y) # 绘制散点图
plt.plot(x, y_predict, color='red') # 预测值x轴 y 轴绘制折线图
plt.show()

点是真实的，线是预测的，如下图发现是欠拟合

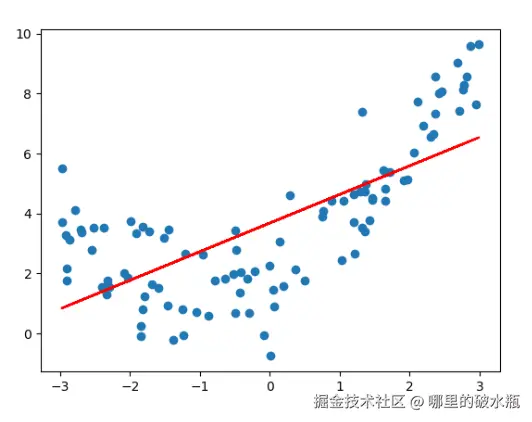
正好拟合

原因就是之前的一列数据，过于简单。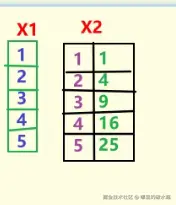

数据不排序，导致来回画导致的

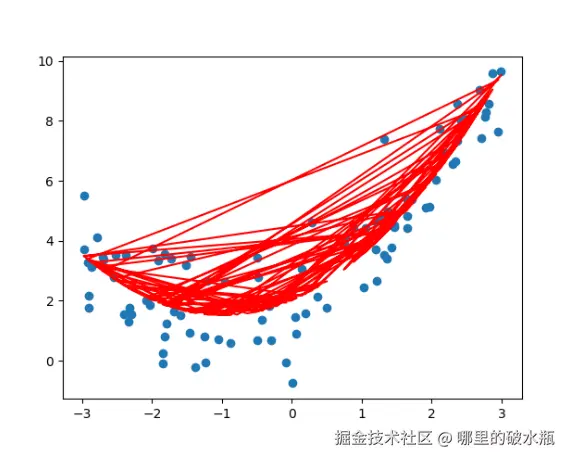
完整代码

py 复制代码 
import matplotlib.pyplot as plt
import numpy as np
from skimage.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.metrics import root_mean_squared_error, mean_absolute_error

# TODO: 设置随机种子
# 设置随机数种子
np.random.seed(666)

# 生成 x 轴数据，100 个
x = np.random.uniform(-3, 3, size=100)

# TODO: y 这样写，是为了 人为构造一份接近真实世界的数据

# 基于x轴的值，结合线性公式，生成y轴的值
# 问题一线性回归公式：y = kx+b，这里为了数据更好，加入噪声...
# 即：y = 0.5x² + x + 2 + 噪声(正态分布生成的随机数)
# np.random.normal(0, 1, size=100) 的意思是，生成正态分布的随机数，均值为0，标准差为1，大小为100
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

print(f'查看数据x：{x}')
print(f'查看数据集y：{y}')

# TODO：2. 数据预处理
X1 = x.reshape(-1, 1)
print(f'处理后的数据集X：{X1}')
# 创建第二列，给每个数据开个平方
X2 = np.hstack([X1, X1 ** 2])
print(f'处理后的数据集X：{X2}') # [[x1, x1²], [x2, x2²], [x3, x3²], ...]

# TODO: 3. 创建模型（算法）对象
estimator = LinearRegression()
estimator.fit(X2, y)

# TODO: 4. 模型预测
y_predict = estimator.predict(X2)

# TODO: 5. 模型评估
print(f'均方误差：{mean_squared_error(y, y_predict)}')
print(f'均方根误差：{root_mean_squared_error(y, y_predict)}')
print(f'平均绝对误差：{mean_absolute_error(y, y_predict)}')

# TODO：6. 绘制图形
plt.scatter(x, y) # 绘制散点图

# 根据x去从小到大排序，并返回索引
# 返回所有后，y_predict 根据索引取出来元素，也就是排序了
y_ = y_predict[np.argsort(x)]
plt.plot(np.sort(x), y_, color='red') # 预测值x轴 y 轴绘制折线图
plt.show()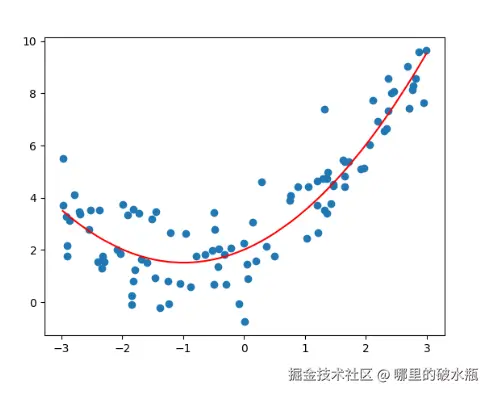

过拟合

就是多增加一些无用的列，学习到很多无用的东西。模型变的复杂。

py 复制代码 
import matplotlib.pyplot as plt
import numpy as np
from skimage.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.metrics import root_mean_squared_error, mean_absolute_error

# TODO: 设置随机种子
# 设置随机数种子
np.random.seed(666)

# 生成 x 轴数据，100 个
x = np.random.uniform(-3, 3, size=100)

# TODO: y 这样写，是为了 人为构造一份接近真实世界的数据

# 基于x轴的值，结合线性公式，生成y轴的值
# 问题一线性回归公式：y = kx+b，这里为了数据更好，加入噪声...
# 即：y = 0.5x² + x + 2 + 噪声(正态分布生成的随机数)
# np.random.normal(0, 1, size=100) 的意思是，生成正态分布的随机数，均值为0，标准差为1，大小为100
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

print(f'查看数据x：{x}')
print(f'查看数据集y：{y}')

# TODO：2. 数据预处理
X1 = x.reshape(-1, 1)
print(f'处理后的数据集X：{X1}')
# 创建第二列，给每个数据开个平方
X2 = np.hstack([X1, X1 ** 2, X1 ** 3, X1 ** 4, X1 ** 5, X1 ** 6, X1 ** 7, X1 ** 8, X1 ** 9, X1 ** 10])
print(f'处理后的数据集X：{X2}') # [[x1, x1²], [x2, x2²], [x3, x3²], ...]

# TODO: 3. 创建模型（算法）对象
estimator = LinearRegression()
estimator.fit(X2, y)

# TODO: 4. 模型预测
y_predict = estimator.predict(X2)

# TODO: 5. 模型评估
print(f'均方误差：{mean_squared_error(y, y_predict)}')
print(f'均方根误差：{root_mean_squared_error(y, y_predict)}')
print(f'平均绝对误差：{mean_absolute_error(y, y_predict)}')

# TODO：6. 绘制图形
plt.scatter(x, y) # 绘制散点图

# 根据x去从小到大排序，并返回索引
# 返回所有后，y_predict 根据索引取出来元素，也就是排序了
y_ = y_predict[np.argsort(x)]
plt.plot(np.sort(x), y_, color='red') # 预测值x轴 y 轴绘制折线图
plt.show()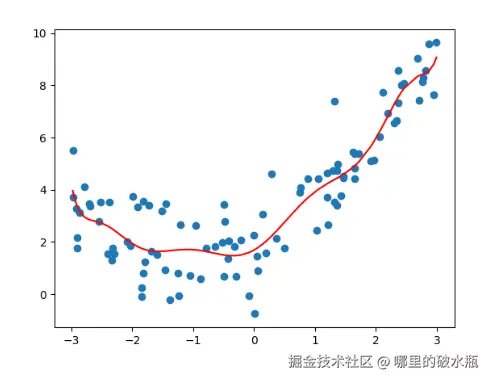

解决方案

欠拟合出现的原因

学习到数据的特征过少

解决方案

  • 添加其他特征
  • 组合、泛化、相关性三类特征是特征添加的重要手段
  • 添加多项式特征项
  • 模型过于简单时的常用套路，例如将线性模型通过添加二次项或三次项使模型泛化能力更强

过拟合出现的原因

原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点

解决方案

  • 重新清洗数据：对于过多异常点数据、数据不纯的地方再处理
  • 增大数据的训练量：对原来的数据训练的太过了，增加数据量的情况下，会缓解
  • 正则化：解决模型过拟合的方法，在机器学习、深度学习中大量使用
  • 减少特征维度，防止维灾难：由于特征多，样本数量少，导致学习不充分，泛化能力差。

正则化处理方案

假设权重都是 0.2，最后一列是数据异常，相对于其他列过高或者过低，此时应该降低最后一列权重。

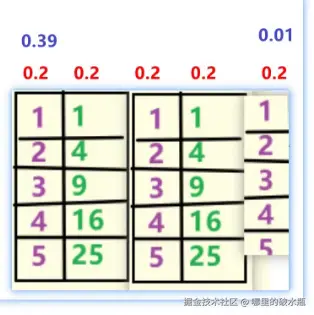
正则化概念（出现的原因）

在模型训练时，数据中有些特征影响模型复杂度、或者某个特征的异常值较多，所以要尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化。

正则化如何消除异常点带来的w值过大过小的影响？

  • 在损失函数中增加正则化项
  • 分为L1正则化、L2正则化

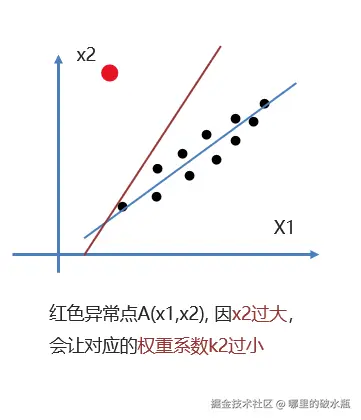
L1 正则化 / L2 正则化

概述：正则化：是一种对模型复杂度的控制的一种手段，通过降低特征的权重实现。

分类：

  • L1：Lasso模块，会降低权重，甚至可能降为 0 -> 特征选取
  • L2：Ridge模块，会降低权重，不会降为 0，也叫岭回归

注意：正则化只是在线性回归的基础上，加上了对系数大小的约束或惩罚。

只需要修改

py 复制代码 
# L1 正则，参数 alpha: 惩罚系数，系数越大，正则化项权重越小
estimator = Lasso(alpha=0.2)
# L2 正则
estimator = Ridge(alpha=0.1)

完整代码

py 复制代码 
import matplotlib.pyplot as plt
import numpy as np
from skimage.metrics import mean_squared_error
from sklearn.linear_model import Lasso, Ridge
from sklearn.metrics import root_mean_squared_error, mean_absolute_error

# TODO: 设置随机种子
# 设置随机数种子
np.random.seed(666)

# 生成 x 轴数据，100 个
x = np.random.uniform(-3, 3, size=100)

# TODO: y 这样写，是为了 人为构造一份接近真实世界的数据

# 基于x轴的值，结合线性公式，生成y轴的值
# 问题一线性回归公式：y = kx+b，这里为了数据更好，加入噪声...
# 即：y = 0.5x² + x + 2 + 噪声(正态分布生成的随机数)
# np.random.normal(0, 1, size=100) 的意思是，生成正态分布的随机数，均值为0，标准差为1，大小为100
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

print(f'查看数据x：{x}')
print(f'查看数据集y：{y}')

# TODO：2. 数据预处理
X1 = x.reshape(-1, 1)
print(f'处理后的数据集X：{X1}')
# 创建第二列，给每个数据开个平方
X2 = np.hstack([X1, X1 ** 2, X1 ** 3, X1 ** 4, X1 ** 5, X1 ** 6, X1 ** 7, X1 ** 8, X1 ** 9, X1 ** 10])
print(f'处理后的数据集X：{X2}')  # [[x1, x1²], [x2, x2²], [x3, x3²], ...]

# TODO: 3. 创建模型（算法）对象
# L1 正则， 参数 alpha: 惩罚系数，系数越大，正则化项权重越小
# estimator = Lasso(alpha=0.1)
# L2 正则
estimator = Ridge(alpha=0.1)
estimator.fit(X2, y)

# TODO: 4. 模型预测
y_predict = estimator.predict(X2)

# TODO: 5. 模型评估
print(f'均方误差：{mean_squared_error(y, y_predict)}')
print(f'均方根误差：{root_mean_squared_error(y, y_predict)}')
print(f'平均绝对误差：{mean_absolute_error(y, y_predict)}')

# TODO：6. 绘制图形
plt.scatter(x, y)  # 绘制散点图

# 根据x去从小到大排序，并返回索引
# 返回所有后，y_predict 根据索引取出来元素，也就是排序了
y_ = y_predict[np.argsort(x)]
plt.plot(np.sort(x), y_, color='red')  # 预测值x轴 y 轴绘制折线图
plt.show()

总结

欠拟合

  • 在训练集上表现不好，在测试集上表现不好
  • 解决方法，继续学习
    • 添加其他特征项
    • 添加多项式特征

过拟合

  • 在训练集上表现好，在测试集上表现不好
  • 解决方法
    1. 重新清洗数据集
    2. 增大数据的训练量
    3. 正则化
    4. 减少特征维度

逻辑回归

底层依赖于线性回归。

解决二分类的问题

把线性回归模型的结果输入给激活函数 Sigmoid 计算出值，假设0.5，超过是一类，不超过是一类

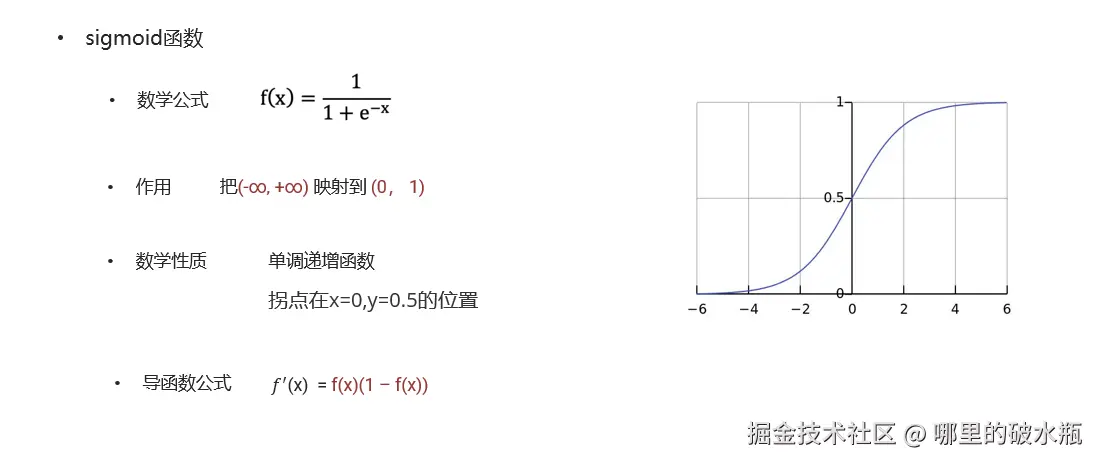
  1. 激活函数 sigmoid 作用？
    • 作用：把数值 映射到 (0， 1）
  2. 极大似然估计？
    • 通过极大化概率事件，来估计最优参数
  3. 对数函数
    • <math xmlns="http://www.w3.org/1998/Math/MathML"> l o g a M N = l o g a M + l o g a N log_a MN = log_a M+log_a N </math>logaMN=logaM+logaN
    • <math xmlns="http://www.w3.org/1998/Math/MathML"> l o g a M n = n l o g a M log_aM^n = nlog_aM </math>logaMn=nlogaM

概念

  • 一种分类模型，把线性回归的输出，作为逻辑回归的输入。
  • 输出是（0, 1）之间的值

思想

  1. 利用线性模型 f(x) = w^Tx + b 根据特征的重要性计算出一个值
  2. 再使用 sigmoid 函数将 f(x) 的输出值映射为概率值
    • 设置阈值(eg：0.5)，输出概率值大于 0.5，则将未知样本输出为 1 类
    • 否则输出为 0 类

总结

逻辑回归原理

  • 思想：解决分类问题，把线性回归的输出作为逻辑回归的输入

逻辑回归的损失函数 -- 对数似然损失

  • 损失函数设计思想：预测值为A、B 2个类别，真实类别所在的位置，概率值越大越好

API 练习

反例：也叫假例，默认数量少的是正例

  • 当是正例的时候，概率越大越好
  • 当是反例的时候：概率越小越好

概述：属于分类算法的一种，一般是二分法。

  1. 基于线性回归，结合特征值，计算出标签值。
  2. 把上述算出来的标签值传给激活函数(Sigmoid)，映射成 0，1 区间的值。
  3. 结合手动设置的阈值，来划分区域
    • 例如：阈值 = 0.6，则 > 0.6 A类，否则 B 类。

损失函数：

  • 先基于极大似然函数计算，然后转成对数似然函数，结合梯度下降，计算最小值即可。

总结：

  1. 逻辑回归原理：把线性回归的输出，作为逻辑回归的输入
  2. 默认情况下：采用样本少当作正例，其他是反例(也叫：假例)
  3. (逻辑回归)损失函数的设计原则：真实值是正例的情况下，概率值越大越好。
py 复制代码 
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# TODO：1. 准备数据
data = pd.read_csv(r'E:\BaiduNetdiskDownload\Heima\25年8月完结 持续更新版本' \
                   r'\源码课件软件\04 正课_机器学习-V6-25年7月版本-8天-AI版本\05-逻辑回归\03-代码\breast-cancer-wisconsin.csv')
# 看不到空值，因为 ? 标记的空
# print(data.info())

# TODO：2. 数据的预处理
# 用 np.NaN 来替换
data.replace('?', np.nan, inplace=True)
# 删除缺失值，按行
data.dropna(axis=0, inplace=True)
# print(data.info())

# TODO：3. 特征工程，特征提取，特征预处理，特征降维，特征选取，特征组合
# 获取特征值 和 目标值(标签值)
x = data.iloc[:, 1:-1] # 从索引为1的列开始获取，直至最后一列不包含。
# y = data.iloc[:, -1]
# y = data['Class']
y = data.Class

# print(len(x), len(y))

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=22)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# TODO：4. 模型训练
# 逻辑回归模型
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

# TODO：5. 模型预测
y_predict = estimator.predict(x_test)
print('预测结果为：', y_predict)

# TODO：6. 模型评估
print('准确率：', estimator.score(x_test, y_test))
print('准确率：', accuracy_score(y_test, y_predict))

思考

仅仅靠正确率，能衡量逻辑回归结果吗？肯定是不可以的，因为只知道正确率，不知道到底哪些是预测成功了，哪些是预测失败了，所以为了进一步的评估，我们需要加入：混淆矩阵，精确率（掌握），召回率（掌握），F1 值（F1-score）（掌握），ROC 曲线（了解），AUC 值（了解）。

混淆矩阵

默认是将分类少的当作正例

已知 恶为正例，良为反例

  • 正例有6个，预测结果 6恶，所以正例是 6，假例是0
  • 假例有4个，预测结果 1良，所以正例是 3，假例是1

此外还要评估预测结果，根据预测结果选择使用的模型。

注意：TP+FN+FP+TN = 总样本数量

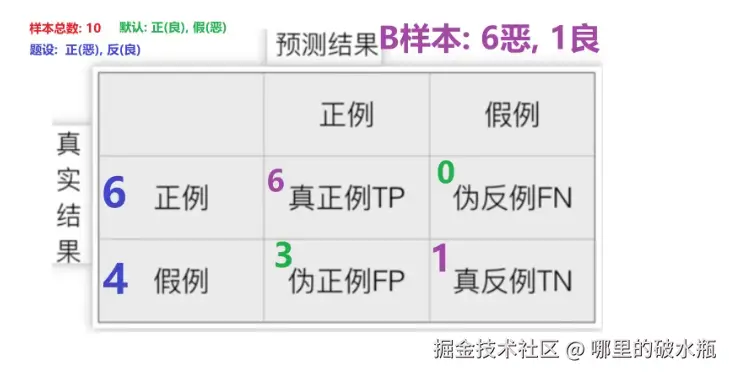
案例

py 复制代码 
# 混淆
import pandas as pd
from sklearn.metrics import confusion_matrix

# TODO: 1. 定义数据集，表示：真实样本(共计10个，6个恶心，4个良性) = 设置，恶性（正例）良性（反例）

y_train = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性', '良性', '良性', '良性']
# TODO: 2. 定义标签名
label = ['恶性', '良性']
df_label = ['恶性(正例)', '良性(反例)']
# TODO: 3. 预测结果A，预测对了3个恶性肿瘤，4个良性肿瘤。
y_predA = ['恶性', '恶性', '恶性', '良性', '良性', '良性', '良性', '良性', '良性', '良性']

# TODO：4. 将真实值和预测值传递给混淆矩阵
# 参数一：真实值，参数二：预测值，参数三：标签（后面计算用的，打印的时候不会出现）
cm_A = confusion_matrix(y_train, y_predA, labels=label)
print(f'混淆矩阵A\n{cm_A}') # [[3 3] [0 4]]

# TODO: 5. 把混淆矩阵转成 DataFrame
df_A = pd.DataFrame(cm_A, index=df_label, columns=df_label)
print(f'混淆矩阵A\n{df_A}')
#        恶性(正例)  良性(反例)
# 恶性(正例)       3       3
# 良性(反例)       0       4

# TODO 6. 测试结果B
y_predB = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性']
cm_B = confusion_matrix(y_train, y_predB, labels=label)
print(f'混淆矩阵B\n{cm_B}')

分类评估方法

准确率，查准率

召回率，查全率

F1

若对模型的精度和找回率都有要求，使用 F1。

案例

逻辑回归 评估方式：

准确率

预测正确的 / 样本总数，即：(tp + tn) / 样本总数

精确率(查准率，Precision)

真正例 / (真正例 + 伪正例)，即：to / (tp + fp)

真正例在预测伪正例的结果中的占比

召回率（查重率，Recall）

真正例 / （真正例 + 伪反例），即：tp / (tp + fn)

真正例在真实正例样本中的样本的占比

F1 值（F1-Score）：

2 * 精确率 * 召回率 / (精确率 + 召回率)

既要考虑精确率，还要考虑召回率的情况

基于上面的案例计算

  • pos_label：指定正例是那个，如果不指定会报错，其中 labels 指定告诉 sklearn 有哪些类别
py 复制代码 
from sklearn.metrics import precision_score, recall_score, f1_score

# 精确率
print(f'预测结果A的精确率：{precision_score(y_train, y_predA, pos_label="恶性")}') # 预测结果A的精确率：1.0
# 召回率
print(f'预测结果B的召回率：{recall_score(y_train, y_predB, pos_label="恶性")}') # 预测结果B的召回率：1.0
# F1 值
print(f'预测结果B的F1值：{f1_score(y_train, y_predB, pos_label="恶性")}') # 预测结果B的F1值：0.8

AUC 指标和 ROC 曲线

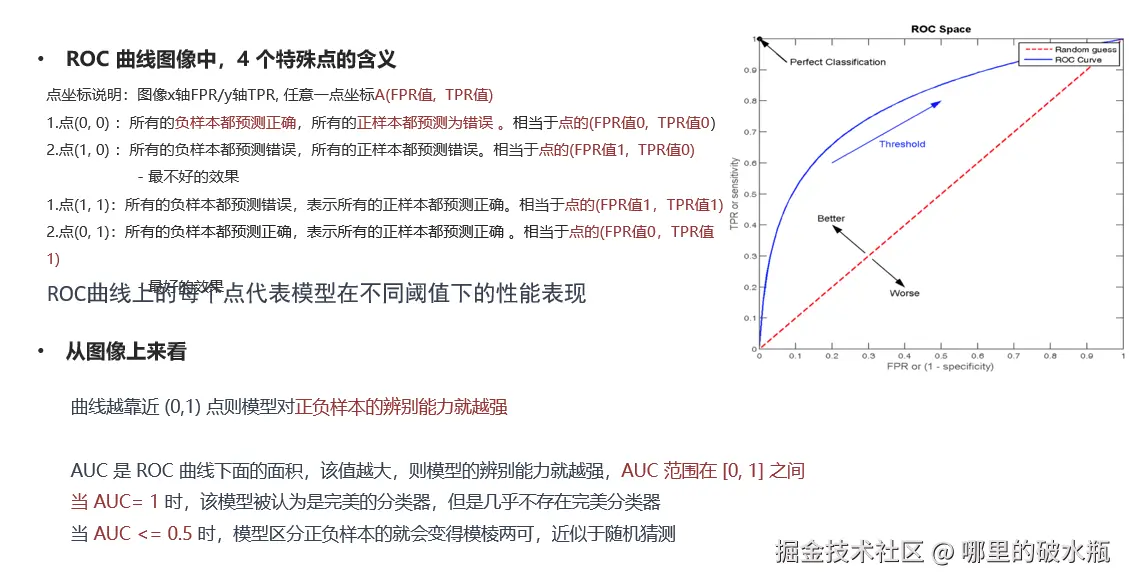
案例

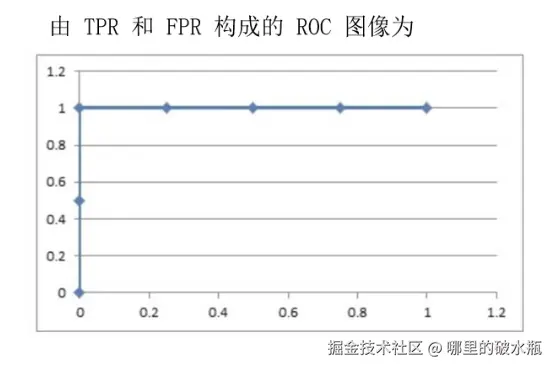
  • AUC 是 ROC 曲线下方的面积，用于比较分类器的性能
  • ROC 曲线用于评估二元分类模型的性能

数据预处理

把 Object 类型处理一下

原数据 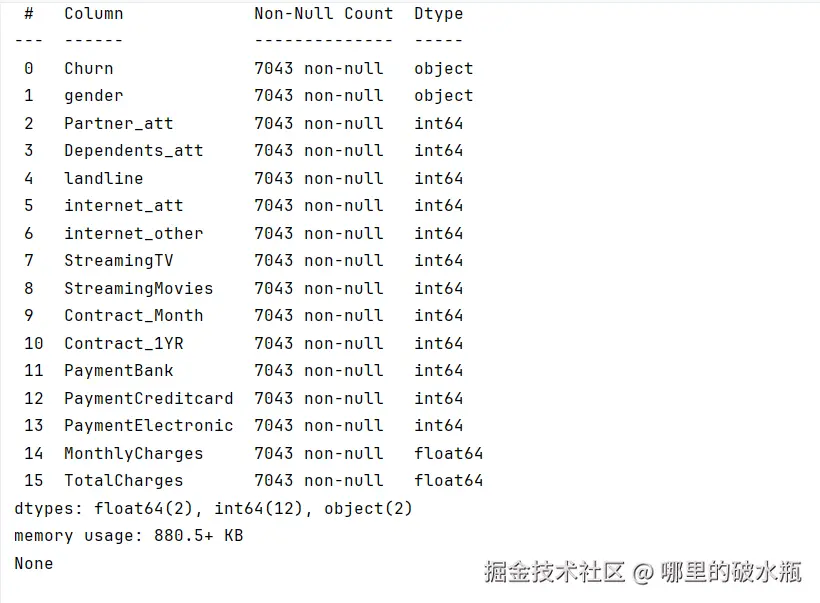处理之后

可以发现把object改成了 bool，多了两列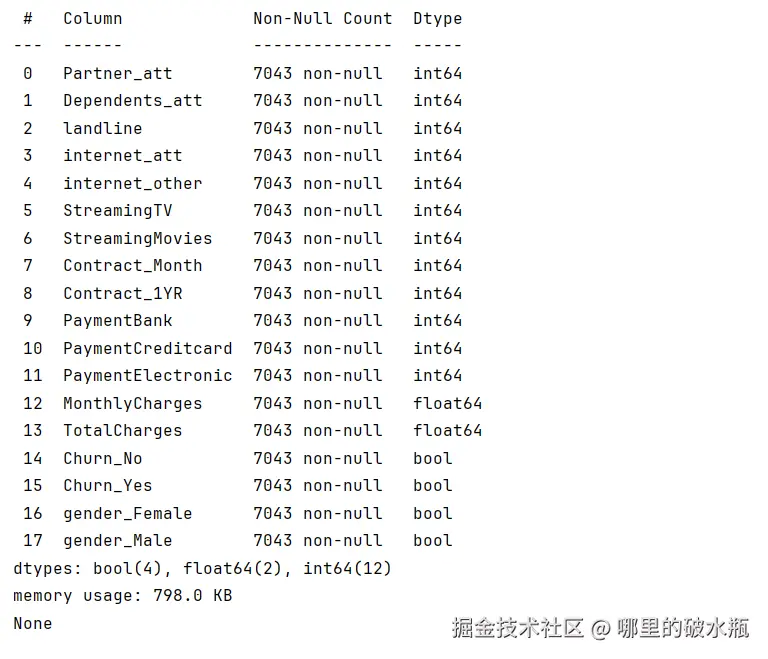

py 复制代码 
import pandas as pd

# TODO: 1. 读取数据
data = pd.read_csv('./churn.csv')
# print(data.info())

# 因为上述的 Churn，gender 是字符串类型，
# 使用 热编码 one-hot 处理
data = pd.get_dummies(data)
# print(data.info())

# 删除多余的两列
data.drop(columns=['gender_Male', 'Churn_No'], axis=1, inplace=True)

# 修改列名
data.rename(columns={'Churn_Yes': 'flag'}, inplace=True)
print(data.info())

# 查看数据是否是均衡的，发现流失的用户是少的
print(data.flag.value_counts()) # True 流失的 1869

数据可视化

py 复制代码 
import matplotlib.pyplot as plt
import seaborn as sns

# TODO: 2. 绘制会员流失情况
# Contract_Month 是否是月度会
# 流失情况分类，False 不流失
sns.countplot(data, x='Contract_Month', hue='flag')
plt.show()

模型预测和评估

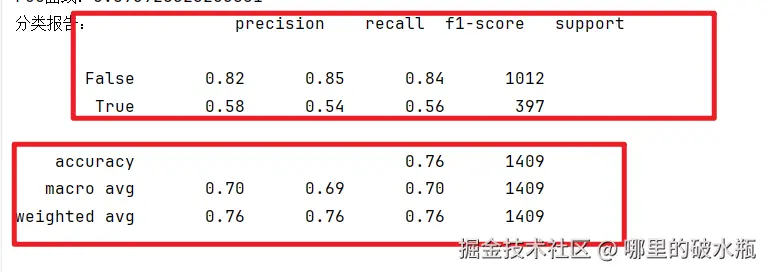
分类评估报告，内容解释

参数 macro avg 的意思是宏平均，是指所有的分类器，都按照macro的方式，计算平均值，不考虑样本的权重，直接平均，跟样本的数量和权重无关，所有的特征权重都是一样的，适合数据集比较平衡的情况。

参数 weighted avg 的意思是：权重平均，是指所有的分类器，都按照 weighted 的方式，计算平均值，考虑样本的权重，根据样本的权重计算平均值，适合数据集比较不平衡的情况。

py 复制代码 
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, \
    classification_report
from sklearn.model_selection import train_test_split

# TODO: 1. 读取数据
l = r'E:\BaiduNetdiskDownload\Heima\25年8月完结 持续更新版本\源码课件软件\04 正课_机器学习-V6-25年7月版本-8天-AI版本\05-逻辑回归\03-代码'

data = pd.read_csv(l + '\churn.csv')
data = pd.get_dummies(data)
data.drop(columns=['gender_Male', 'Churn_No'], axis=1, inplace=True)
data.rename(columns={'Churn_Yes': 'flag'}, inplace=True)

# TODO: 2. 绘制会员流失情况
# Contract_Month 是否是月度会
# 流失情况分类，False 不流失
# sns.countplot(data, x='Contract_Month', hue='flag')
# plt.show()

# TODO: 3. 模型训练评估

# 关键特征和标签选取
y = data['flag']
x = data[['Contract_Month', 'PaymentCreditcard', 'internet_other']]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=22)

# 创建逻辑回归模型，并训练
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

# 模型预测
y_predict = estimator.predict(x_test)
print(f'预测值为：{y_predict}')

# TODO 4. 模型评估
print(f'准确率：{estimator.score(x_test, y_test)}')
print(f'准确率：{accuracy_score(y_test, y_predict)}') # 真实值，预测值
print(f'精确率：{precision_score(y_test, y_predict)}')
print(f'召回率：{recall_score(y_test, y_predict)}')
print(f'F1值:{f1_score(y_test, y_predict)}')
print(f'roc曲线：{roc_auc_score(y_test, y_predict)}')

print(f'分类报告：{classification_report(y_test, y_predict)}')
相关推荐
0思必得022 分钟前
[Web自动化] Selenium处理动态网页
前端·爬虫·python·selenium·自动化
韩立学长28 分钟前
【开题答辩实录分享】以《基于Python的大学超市仓储信息管理系统的设计与实现》为例进行选题答辩实录分享
开发语言·python
大山同学30 分钟前
图片补全-Context Encoder
人工智能·机器学习·计算机视觉
qq_1927798731 分钟前
高级爬虫技巧：处理JavaScript渲染（Selenium）
jvm·数据库·python
u0109272711 小时前
使用Plotly创建交互式图表
jvm·数据库·python
爱学习的阿磊1 小时前
Python GUI开发：Tkinter入门教程
jvm·数据库·python
Imm7771 小时前
中国知名的车膜品牌推荐几家
人工智能·python
tudficdew2 小时前
实战：用Python分析某电商销售数据
jvm·数据库·python
陈天伟教授2 小时前
人工智能应用-机器听觉：15. 声纹识别的应用
人工智能·神经网络·机器学习·语音识别
sjjhd6522 小时前
Python日志记录（Logging）最佳实践
jvm·数据库·python
热门推荐
01GitHub 镜像站点02Clawdbot 中文汉化版 接入微信、飞书03OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书042026美赛A题智能手机电池续航时间预测的连续时间数学模型05OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)06UV安装并设置国内源07Linux下V2Ray安装配置指南08Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services092025 年大语言模型发展回顾：关键突破、意外转折与 2026 年展望10【Milvus】向量数据库pymilvus使用教程