推荐从第二章开始看---
从时域到复频域t->s & 传递函数&超前滞后校正
又名:论螺旋线的无处不在
文章目录
- [从时域到复频域t->s & 传递函数&超前滞后校正](#从时域到复频域t->s & 传递函数&超前滞后校正)
-
- [1 复指数 e s t e^{st} est](#1 复指数 e s t e^{st} est)
-
- [1.1 数学拆解:欧拉公式是核心](#1.1 数学拆解:欧拉公式是核心)
- [1.2 几何直观:3D 螺旋线](#1.2 几何直观:3D 螺旋线)
- [1.3 三种情况的物理对应(控制人的视角)](#1.3 三种情况的物理对应(控制人的视角))
- 示意曲线图绘制代码
- s的含义
-
- 身份1:s作为"动作指令"(Operator)
- [身份2:s作为"信号特征"(Signal Signature)](#身份2:s作为“信号特征”(Signal Signature))
- 身份3:s作为"系统零点"(Root)
- [s+z 的物理意义:微分 + 放大](#s+z 的物理意义:微分 + 放大)
- 1/(s+p)的物理意义:积分+遗忘
- [2 拉普拉斯变换的本质:换一种语言看世界](#2 拉普拉斯变换的本质:换一种语言看世界)
-
- [2.1 为什么要"换语言"?](#2.1 为什么要"换语言"?)
- [2.2 "复频域"拆解:复 + 频](#2.2 "复频域"拆解:复 + 频)
- [2.3 时域 vs 复频域:变量对应关系](#2.3 时域 vs 复频域:变量对应关系)
- [3 传递函数:系统的"性格档案"](#3 传递函数:系统的"性格档案")
-
- [3.1 传递函数是什么?](#3.1 传递函数是什么?)
- [3.2 典型传递函数 (s+z)/(s+p) 的解剖](#3.2 典型传递函数 (s+z)/(s+p) 的解剖)
- [3.3 零点与极点:系统命运的两只手](#3.3 零点与极点:系统命运的两只手)
- [4 零极点位置的魔法:z<p vs z>p](#4 零极点位置的魔法:z
p)
-
- [4.1 频率响应视角:谁是老大?](#4.1 频率响应视角:谁是老大?)
- [4.2 生活类比:水库与瀑布](#4.2 生活类比:水库与瀑布)
- [4.3 阶跃响应的直观理解](#4.3 阶跃响应的直观理解)
- [5 时域 vs 复频域:两套思维工具](#5 时域 vs 复频域:两套思维工具)
-
- [5.1 状态方程:时域的"逐帧分析"](#5.1 状态方程:时域的"逐帧分析")
- [5.2 两种方法的对比](#5.2 两种方法的对比)
- [5.3 平衡点:系统的"舒适区"](#5.3 平衡点:系统的"舒适区")
- [6 完整认知框架:一张地图](#6 完整认知框架:一张地图)
- [7 超前校正与滞后校正:给系统"吃药"](#7 超前校正与滞后校正:给系统"吃药")
-
- [7.1 问题的提出](#7.1 问题的提出)
- [7.2 超前校正:预判大师](#7.2 超前校正:预判大师)
- [7.3 滞后校正:平滑大师](#7.3 滞后校正:平滑大师)
- [7.4 超前滞后对比](#7.4 超前滞后对比)
- [7.5 关键记忆口诀](#7.5 关键记忆口诀)
1 复指数 e s t e^{st} est
复指数 e s t e^{st} est 是正余弦函数(旋转)与实指数函数(缩放)的"合体"。
这就是为什么我们在控制理论和信号处理中如此迷恋复频域( s s s 域)的原因------因为它用一个简单的 e s t e^{st} est ,统一描述了世界上几乎所有的线性运动形式。
1.1 数学拆解:欧拉公式是核心
在复频域中,变量 s s s 是一个复数:
s = σ + j ω s = \sigma + j\omega s=σ+jω
- σ \sigma σ (Sigma):实部,代表衰减或增长。
- ω \omega ω (Omega):虚部,代表旋转或振荡。
根据指数运算法则和欧拉公式 ( e j θ = cos θ + j sin θ e^{j\theta} = \cos\theta + j\sin\theta ejθ=cosθ+jsinθ ), e s t e^{st} est 可展开为:
e s t = e ( σ + j ω ) t = e σ t ⏟ 幅值包络 ⋅ ( cos ( ω t ) + j sin ( ω t ) ) ⏟ 相位旋转 e^{st} = e^{(\sigma + j\omega)t} = \underbrace{e^{\sigma t}}{\text{幅值包络}} \cdot \underbrace{(\cos(\omega t) + j\sin(\omega t))}{\text{相位旋转}} est=e(σ+jω)t=幅值包络 eσt⋅相位旋转 (cos(ωt)+jsin(ωt))
- 后半部分 ( cos ω t + j sin ω t ) (\cos\omega t + j\sin\omega t) (cosωt+jsinωt) :正余弦函数,负责系统震荡。
- 前半部分 e σ t e^{\sigma t} eσt :实数缩放因子,负责控制震荡的幅值变化(增强/减弱)。
1.2 几何直观:3D 螺旋线
复指数 e s t e^{st} est 可直观理解为三维空间中的螺旋线:
- 侧视图(实轴/虚轴视角):投影为正弦波或余弦波(体现振荡特性)。
- 俯视图(复平面视角) : σ = 0 \sigma=0 σ=0 时为圆(等幅旋转), σ ≠ 0 \sigma \neq 0 σ=0 时为螺旋(幅值随时间缩放)。
1.3 三种情况的物理对应(控制人的视角)
极点 s s s 的位置决定了 e s t e^{st} est 的形态,对应机器人系统中三种典型的动态响应:
-
纯虚数 ( s = 0 + j ω s = 0 + j\omega s=0+jω ) ------ 永动级
- 数学特征 : σ = 0 \sigma=0 σ=0 ,幅值包络 e 0 t = 1 e^{0t} = 1 e0t=1 。
- 表达式 : e s t = cos ω t + j sin ω t e^{st} = \cos \omega t + j\sin \omega t est=cosωt+jsinωt 。
- 现象 :等幅震荡(标准正弦波)。
- 实例:无摩擦力的理想单摆。
-
左半平面复数 ( s = − σ + j ω s = -\sigma + j\omega s=−σ+jω , σ > 0 \sigma>0 σ>0 ) ------ 稳定级
- 数学特征 : σ < 0 \sigma < 0 σ<0 ,幅值包络 e − σ t e^{-\sigma t} e−σt 随时间衰减。
- 表达式 : e s t = e − σ t ( cos ω t + j sin ω t ) e^{st} = e^{-\sigma t} (\cos \omega t + j\sin \omega t) est=e−σt(cosωt+jsinωt) 。
- 现象 :衰减震荡(振幅逐渐趋向于0)。
- 实例:推一下四足机器人,晃悠几下后稳稳站住(阻尼作用)。
-
右半平面复数 ( s = σ + j ω s = \sigma + j\omega s=σ+jω , σ > 0 \sigma>0 σ>0 ) ------ 炸机级
- 数学特征 : σ > 0 \sigma > 0 σ>0 ,幅值包络 e σ t e^{\sigma t} eσt 随时间增长。
- 表达式 : e s t = e σ t ( cos ω t + j sin ω t ) e^{st} = e^{\sigma t} (\cos \omega t + j\sin \omega t) est=eσt(cosωt+jsinωt) 。
- 现象 :发散震荡(振幅越来越大,系统崩溃)。
- 实例:麦克风啸叫、PID参数调飞导致机器人剧烈抖动翻车。
e s t e^{st} est 的本质是**"带缩放功能的旋转机"**:
- 虚部 ω \omega ω :贡献正余弦特性(旋转/频率),对应系统的振荡行为。
- 实部 σ \sigma σ :贡献指数特性(缩放/寿命),对应系统的稳定特性。
正因为 e s t e^{st} est 同时包含了"生灭"(实部)和"轮回"(虚部),它才能成为线性微分方程的通解,这也是传递函数中一个 s s s 就能代表两种物理现象的核心原因。
示意曲线图绘制代码
以下是基于 Python + Matplotlib 的示意曲线图代码,可直接在 Ubuntu 22.04 环境中运行(需安装 matplotlib 库:pip install matplotlib)。代码包含三种时域响应曲线 和3D螺旋线几何直观图。
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 全局参数设置
t = np.linspace(0, 5, 500) # 时间序列
sigma1 = 0 # 纯虚数情况
sigma2 = 0 # 衰减情况(左半平面)
sigma3 = 0 # 发散情况(右半平面)
omega = 2 * np.pi # 角频率(统一为2π,对应频率1Hz)
# 三种时域响应曲线(实部随时间变化)
plt.figure(figsize=(12, 6))
# 纯虚数:等幅振荡
y1 = np.cos(omega * t)
plt.plot(t, y1, label=r'纯虚数 $s=j\omega$ (等幅振荡)', color='blue', linewidth=2)
# 左半平面:衰减振荡
y2 = np.exp(-sigma2 * t) * np.cos(omega * t)
plt.plot(t, y2, label=r'左半平面 $s=-\sigma+j\omega$ (衰减振荡)', color='green', linewidth=2)
# 右半平面:发散振荡
y3 = np.exp(sigma3 * t) * np.cos(omega * t)
plt.plot(t, y3, label=r'右半平面 $s=\sigma+j\omega$ (发散振荡)', color='red', linewidth=2)
# 图形美化
plt.axhline(y=0, color='k', linestyle='--', alpha=0.5)
plt.xlabel('时间 t (s)', fontsize=12)
plt.ylabel('实部 $Re[e^{st}]$', fontsize=12)
plt.title('复指数 $e^{st}$ 的三种时域响应', fontsize=14, fontweight='bold')
plt.legend(loc='upper right', fontsize=10)
plt.grid(True, alpha=0.3)
plt.ylim(-5, 5) # 限制y轴范围,突出发散趋势
plt.show()
# 2. 3D螺旋线几何直观图(以衰减振荡为例,s=-0.5+j2π)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
sigma_3d = 0.5
omega_3d = 2 * np.pi
t_3d = np.linspace(0, 4, 1000)
x = np.exp(-sigma_3d * t_3d) * np.cos(omega_3d * t_3d) # 实部
y = np.exp(-sigma_3d * t_3d) * np.sin(omega_3d * t_3d) # 虚部
z = t_3d # 时间轴
# 绘制3D螺旋线
ax.plot(x, y, z, color='purple', linewidth=2, label=r'$e^{st}=e^{(-0.5+j2\pi)t}$ 螺旋线')
ax.set_xlabel('实部 $Re$', fontsize=12)
ax.set_ylabel('虚部 $Im$', fontsize=12)
ax.set_zlabel('时间 t (s)', fontsize=12)
ax.set_title('复指数 $e^{st}$ 的3D螺旋线几何直观', fontsize=14, fontweight='bold')
ax.legend(fontsize=10)
plt.show()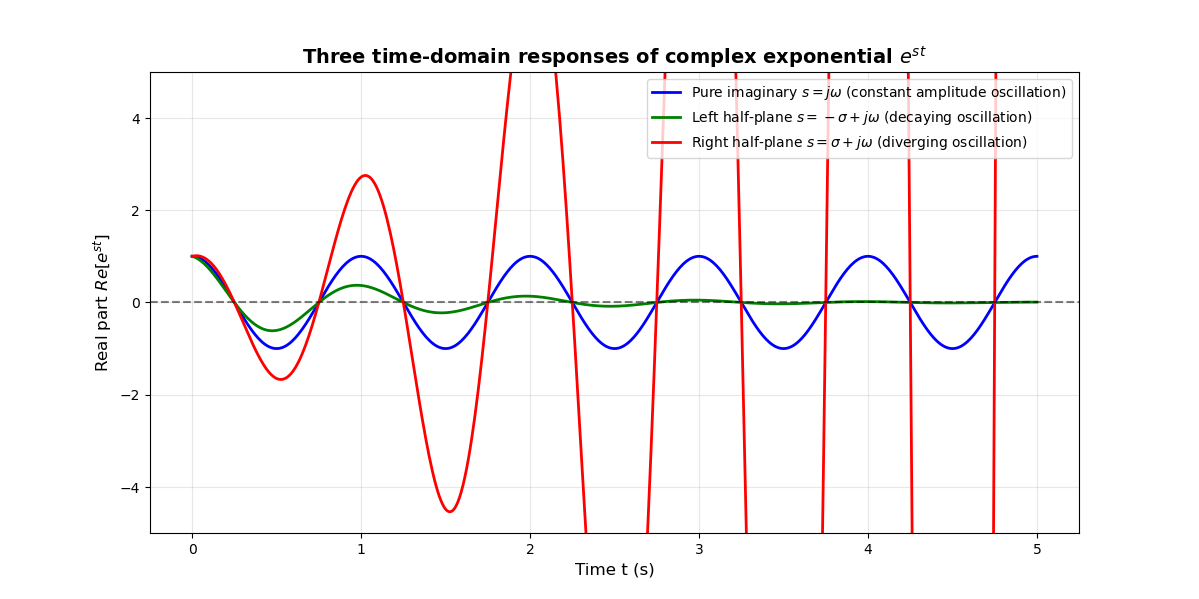
-
三种时域响应曲线
- 蓝色曲线:等幅振荡,振幅始终为1,无衰减或增长。
- 绿色曲线:衰减振荡,振幅被 e − σ t e^{-\sigma t} e−σt 压制,逐渐趋近于0。
- 红色曲线:发散振荡,振幅被 e σ t e^{\sigma t} eσt 放大,快速超出范围(图中限制y轴以展示趋势)。
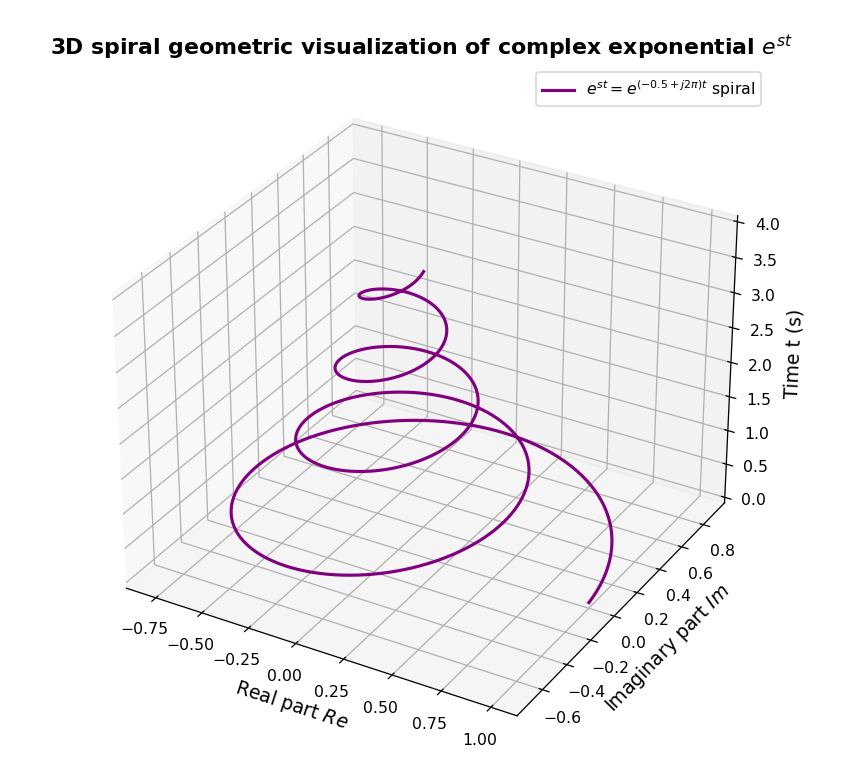
-
3D螺旋线几何直观图
- 以衰减振荡为例,螺旋线的半径随时间减小(体现 e − σ t e^{-\sigma t} e−σt 的缩放作用)。
- 绕z轴旋转的频率由 ω \omega ω 决定(体现正余弦的旋转作用)。
- 若将 σ 3 d \sigma_3d σ3d 改为0,螺旋线变为圆柱螺旋(等幅旋转);改为负数,螺旋线半径随时间增大(发散旋转)。
s的含义
身份1:s作为"动作指令"(Operator)
角色:微分算子
-
语境 :当你看到传递函数 G ( s ) = s G(s) = s G(s)=s 或者 s + z s+z s+z 时。
-
含义 :在这里, s s s 不是一个具体的数,而是一个动作 。在拉普拉斯变换的性质里,乘以 s s s 对应时域的求导(微分) d d t \frac{d}{dt} dtd。
-
物理动作:
-
s s s:表示"对输入求导"。
-
s + z s+z s+z:表示"对输入求导,再加上 z z z 倍的输入"。
-
身份2:s作为"信号特征"(Signal Signature)
角色:复频率
-
语境 :当你描述输入信号 e s t e^{st} est 或分析系统稳定性(极点位置)时。
-
含义 :这里的 s = σ + j ω s = \sigma + j\omega s=σ+jω 是在描述波形的形状。
-
实部 σ = 0 \sigma=0 σ=0 :表示既不发散也不衰减,是等幅震荡(正弦波)。
-
实部 σ ≠ 0 \sigma \neq 0 σ=0:表示波形在变大或变小。
-
s = 0 s=0 s=0 :表示既不震荡也不变化,即直流常量 (DC)。
-
身份3:s作为"系统零点"(Root)
角色:屏蔽器
-
语境 :当你令分子 s + z = 0 s+z=0 s+z=0 求出 s = − z s=-z s=−z 时。
-
s + z s+z s+z的bodet图
text
幅值 (dB)
^
| /
| /
| / 斜率 = +20 dB/dec
| / (微分特性区)
| /
| /
K |---------------------+
| ^
| ω = z
| (转折频率)
--+------------------------------------> 频率 log(ω)- 含义 :这是在寻找一种特定的信号,系统对这种信号完全没反应。
验证零点特性
让我们做一个最直观的数学实验。假设系统的传递函数分子是 s + z s+z s+z(即有一个零点在 − z -z −z)。
-
把 s s s 看作"动作" (身份证1)
系统对输入 u ( t ) u(t) u(t) 的处理方式是: 输出 y ( t ) = d u ( t ) d t + z ⋅ u ( t ) \text{输出 } y(t) = \frac{du(t)}{dt} + z \cdot u(t) 输出 y(t)=dtdu(t)+z⋅u(t)(这就是 s + z s+z s+z 在时域的物理意义:求导 + 比例)
-
给它一个特定的"信号" (身份证2)
我们给系统输入一个特定的指数衰减信号: u ( t ) = e − z t u(t) = e^{-zt} u(t)=e−zt。这个信号的特征指数 (广义频率)正是 s = − z s = -z s=−z。
-
见证奇迹的时刻 (身份证3)
我们将这个信号代入上面的动作中:
-
先求导: d d t ( e − z t ) = − z ⋅ e − z t \frac{d}{dt}(e^{-zt}) = -z \cdot e^{-zt} dtd(e−zt)=−z⋅e−zt
-
再比例: z ⋅ u ( t ) = z ⋅ e − z t z \cdot u(t) = z \cdot e^{-zt} z⋅u(t)=z⋅e−zt
-
相加(输出) :
y ( t ) = ( − z ⋅ e − z t ) + ( z ⋅ e − z t ) = 0 y(t) = (-z \cdot e^{-zt}) + (z \cdot e^{-zt}) = 0 y(t)=(−z⋅e−zt)+(z⋅e−zt)=0
-
输出真的变成了0。
-
s代表微分:是因为这一项确实在对信号进行求导操作。
-
s+z=0代表输出为0 :是指当且仅当 输入信号的形态正好是 e − z t e^{-zt} e−zt 时,微分产生的负值( − z -z −z)正好完全抵消了比例产生的正值( + z +z +z),导致结果为0。
零点理解:纯微分环节示例 我们拿最极端的例子:纯微分环节 G ( s ) = s G(s) = s G(s)=s 。它的零点在哪?令 s = 0 s=0 s=0。这里的 s = 0 s=0 s=0 意味着什么?
-
信号特征 : s = 0 s=0 s=0 (实部虚部均为0) 对应的是直流常量 (Constant, e.g., u ( t ) = 5 u(t) = 5 u(t)=5)。
-
动作机理 : G ( s ) = s G(s)=s G(s)=s 代表求导。
-
结果 :你对常数 5 求导 ( d d t 5 \frac{d}{dt}5 dtd5),结果是多少?是 0!
所以逻辑完全通畅:
因为 s s s 代表微分 ,而 s = 0 s=0 s=0 代表常数 ,常数的微分等于0。所以 s = 0 s=0 s=0 是微分环节的零点。
通俗总结 :1. 传递函数里的 s s s 是信号处理模式(微分)。2. 输入信号里的 s s s 表示复频域的输入信号(波形的频率和衰减率)。3. 零点 表示特殊的复频域信号量。当给系统输入该信号量(特定的波形 e − z t e^{-zt} e−zt)经过系统处理(进行微分+比例运算)后,系统是输出为0。
Y ( s ) = s X ( s ) Y(s)=sX(s) Y(s)=sX(s)
说明:
-
式子中的 X ( s ) X(s) X(s)、 Y ( s ) Y(s) Y(s) 是"复频域信号"(括号里的 s s s 是复频域的标志,代表这两个信号是在复频域下的表达,分别对应时域输入信号 x ( t ) x(t) x(t)、输出信号 y ( t ) y(t) y(t) 的复频域形式);
-
乘在 X ( s ) X(s) X(s)前面的 s s s 不是信号,而是一个"运算模块",它的作用等价于对时域输入信号 x ( t ) x(t) x(t) 做微分操作(即 y ( t ) = d x ( t ) d t y(t) = \frac{dx(t)}{dt} y(t)=dtdx(t),这是复频域的核心特性:时域微分对应复频域"乘 s s s")。
s+z 的物理意义:微分 + 放大
1/(s+p)的物理意义:积分+遗忘
若说 s + z s+z s+z 是 "微分 + 放大"(或者叫"带基准的预测"),那么 1 s + p \frac{1}{s+p} s+p1 最精准的定义是:"积分 + 遗忘"(或者叫 "有损积分"、"泄漏积分")。用工程黑话来说,就是 低通滤波器 (Low Pass Filter)。
直观理解:从"完美存钱罐"到"漏底的钱包" 纯积分 1/s 如同完美的存钱罐:数学上 y ˙ = u \dot{y} = u y˙=u(输出的变化率 = 输入),物理上就像往密封水桶倒水,倒多少存多少永不漏,结果是只要有输入输出就无限增加,易发散;一阶惯性环节 1/(s+p) 则像漏底的钱包(Leaky Integrator)。
-
数学: y ˙ = u \dot{y} = u y˙=u (输出的变化率 = 输入)
-
物理: 你往水桶里倒水,水桶是密封的。你倒多少,它就存多少,永远不漏。
-
结果: 只要有输入,输出就会无限增加,直到无穷大。这叫"无差",但也容易"发散"。
-
数学: y ˙ = u − p ⋅ y \dot{y} = u - p \cdot y y˙=u−p⋅y
-
注意这个公式:你的输入 u u u 在努力让 y y y 增加(积分作用)。但是 − p ⋅ y -p \cdot y −p⋅y 在拖后腿, y y y 越大,漏得越快。
-
物理: 你往水桶里倒水,但水桶底部有个洞(大小由 p p p 决定)。刚开始水位低,漏得慢,水位上升(表现像积分)。水位越高,水压越大,漏得越快。最后,当你倒水的速度和漏水的速度相等时,水位就不涨了,维持在一个平衡高度。
-
"遗忘"的含义: 它不再无限记忆历史了。很久以前倒进去的水,早就漏光了。它只记得"最近"一段时间的输入。
极点p的影响:遗忘速度与系统惯性
这个 p p p (极点) 决定了**"遗忘的速度",也就是系统的"惯性"**。若 p p p 很大(极点远离原点),漏得快,系统"记性不好",反应极快但存不住东西,传递函数接近常数(比例环节);若 p p p 很小(极点靠近原点),漏得慢,系统"记性很好",接近纯积分 1 s \frac{1}{s} s1,反应慢、惯性大,能平滑高频噪声。从频域视角看, 1 s + p \frac{1}{s+p} s+p1 的 Bode 图幅频特性如下:
text
幅值 (dB)
^
|
K|-----------------------\
| \
| \
| \ 斜率 = -20 dB/dec
| \ (积分特性区)
| \
--+-----------------------------+---------> 频率 log(ω)
| ^
0 ω = p
(转折频率)-
低频段 (ω < p) :输入变化太慢,漏水速度完全跟得上倒水速度,系统表现为常数增益 (Gain = 1 / p 1/p 1/p),此时并非积分而是比例放大;
-
高频段 (ω > p):输入变化太快,水来不及漏出,"洞"的影响被忽略,系统回归纯积分特性(斜率 -20dB/dec)。
-
输入变化太慢,漏水速度完全跟得上倒水速度。系统表现为一个常数增益 (Gain = 1 / p 1/p 1/p)。结论: 此时它不是积分,是比例放大。
-
输入变化太快(比如倒水的速度像机关枪一样抖动),水来不及从洞里漏出去。此时"洞"的影响被忽略了,系统表现得像一个没有洞的桶。结论: 此时它回归了本性,表现为纯积分 (斜率 -20dB/dec)。
工程应用场景
-
场景一:传感器滤波(LPF),读取陀螺仪角速度时数据抖动大,代码"vel_filtered = 0.9 * vel_filtered + 0.1 * vel_raw"本质是离散化的 1 s + p \frac{1}{s+p} s+p1,通过"积分"新测量值、"遗忘"旧值滤除高频噪声;
-
场景二:电机模型,给电机电压(输入)后转速(输出)缓慢爬升,因电机转子惯性、线圈电感等物理特性天然是 1 s + p \frac{1}{s+p} s+p1,电压试图"积分"出速度,反电动势和摩擦力( p p p)消耗能量,最终达到稳态转速。
-
当读取陀螺仪的角速度,数据抖动很大。你写了一行代码:vel_filtered = 0.9 * vel_filtered + 0.1 * vel_raw。本质: 这就是离散化的 1 s + p \frac{1}{s+p} s+p1。它在"积分"新的测量值,同时"遗忘"旧的测量值,从而滤除高频噪声。
-
给电机电压(输入),电机转速(输出)不会瞬间跳变,而是慢慢爬升。本质: 电机转子有惯性,线圈有电感。这些物理特性天然就是 1 s + p \frac{1}{s+p} s+p1。电压试图"积分"出速度,但反电动势和摩擦力(那个 p p p)在不断消耗能量,最终达到稳态转速。
总结 : s + z s+z s+z (零点) = 微分 + 预测(看未来趋势,太敏感); 1 s + p \frac{1}{s+p} s+p1 (极点) = 积分 + 遗忘/阻尼(看过去历史,懂淡忘,显稳重)。所以, 1 s + p \frac{1}{s+p} s+p1 是"不但能积累经验,还懂得适时放下"的智慧系统。
2 拉普拉斯变换的本质:换一种语言看世界
2.1 为什么要"换语言"?
想象你是一位侦探,需要分析一段复杂的音乐录音。
┌─────────────────────────────────────────────────────────────────────┐
│ 两种分析录音的方式 │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ 【时域视角】逐秒听 【频域视角】分析成分 │
│ │
│ ♪~~♫~~♪~~♫ 低音:■■■■□□□□ │
│ ↓ ↓ ↓ ↓ ↓ 中音:■■■■■■□□ │
│ t=0 t=1 t=2 t=3... 高音:■■□□□□□□ │
│ │
│ "这一秒声音大, "哦!这首歌低音强, │
│ 下一秒声音小..." 高音弱,是R&B风格" │
│ │
│ → 适合追踪细节变化 → 适合理解整体特征 │
└─────────────────────────────────────────────────────────────────────┘控制系统也是如此:时域中我们看到信号随时间起伏跌宕,但很难一眼看出系统的"性格"。转到复频域后,系统的本质特征一目了然。
2.2 "复频域"拆解:复 + 频
复频率 s = σ + jω ,这个神秘符号其实在描述一类特殊的信号:
┌─────────────────────────────────────────────────────────────────────┐
│ 复指数信号:e^(st) = e^(σt) · e^(jωt) │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ ┌─────────────┐ │
│ e^(σt) × │ e^(jωt) │ = 完整的复指数信号 │
│ ───── └─────────────┘ │
│ ↓ ↓ │
│ 【σ:实部】 【ω:虚部】 │
│ "生死簿" "心跳节奏" │
│ │
│ ┌────────────────────────────────────────────────────────────┐ │
│ │ σ < 0:衰减(像放气的气球) ω:振荡的快慢 │ │
│ │ ╲ ╱ │ │
│ │ σ = 0:等幅(像理想钟摆) ╳ ω大→振荡快 │ │
│ │ ╱ ╲ ω小→振荡慢 │ │
│ │ σ > 0:增长(像失控的核反应) ω=0→不振荡 │ │
│ └────────────────────────────────────────────────────────────┘ │
└─────────────────────────────────────────────────────────────────────┘一个直观类比:
把信号想象成一个人的心电图:
- σ(实部)= 这个人的生命力是在增强、稳定还是衰减?
- ω(虚部)= 心脏跳动的频率是多少?
2.3 时域 vs 复频域:变量对应关系
┌─────────────────────────────────────────────────────────────────────┐
│ 两个世界的映射关系 │
├──────────────────────────┬──────────────────────────────────────────┤
│ 时域世界 (t) │ 复频域世界 (s) │
├──────────────────────────┼──────────────────────────────────────────┤
│ │ │
│ 时间 t(秒、分...) │ 复频率 s = σ + jω │
│ │ │
│ 信号 x(t) │ 频谱 X(s) = ∫x(t)e^(-st)dt │
│ "随时间变化的故事" │ "故事中各成分的配方" │
│ │ │
│ 微分 dx/dt │ 乘以 s:sX(s) ← 变简单了! │
│ "变化的速度" │ "只是乘个数" │
│ │ │
│ 积分 ∫x dt │ 除以 s:X(s)/s ← 也变简单了! │
│ "累积的总量" │ "只是除个数" │
│ │ │
├──────────────────────────┴──────────────────────────────────────────┤
│ │
│ 🎯 核心价值:复频域把微积分运算变成了代数运算 │
│ 就像对数把乘除变成加减,是一种"降维打击" │
│ │
└─────────────────────────────────────────────────────────────────────┘3 传递函数:系统的"性格档案"
3.1 传递函数是什么?
想象你面前有一个黑箱子,你往里扔不同的球(输入),它会以特定方式抛出球(输出):
┌─────────────────────┐
输入信号 │ │ 输出信号
U(s) ──────▶ │ G(s) = Y(s)/U(s) │ ──────▶ Y(s)
"刺激" │ "系统的性格" │ "反应"
└─────────────────────┘
传递函数 G(s) 就是:这个黑箱的"刺激-反应"规律3.2 典型传递函数 (s+z)/(s+p) 的解剖
┌─────────────────────────────────────────────────────────────────────┐
│ │
│ s + z │
│ G(s) = ───────── │
│ s + p │
│ │
│ ┌──────────────────┴──────────────────┐ │
│ ↓ ↓ │
│ ╔═══════════════╗ ╔═══════════════╗ │
│ ║ 分子 (s+z) ║ ║ 分母 (s+p) ║ │
│ ║───────────────║ ║───────────────║ │
│ ║ 零点 z 的位置 ║ ║ 极点 p 的位置 ║ │
│ ║ ║ ║ ║ │
│ ║ 当 s = -z 时 ║ ║ 当 s = -p 时 ║ │
│ ║ 分子 = 0 ║ ║ 分母 = 0 ║ │
│ ║ 输出被"消灭" ║ ║ 输出"爆炸" ║ │
│ ╚═══════════════╝ ╚═══════════════╝ │
│ │
└─────────────────────────────────────────────────────────────────────┘为什么是这种形式?
传递函数来源于微分方程的因式分解:
原始微分方程: a₁(dy/dt) + a₀y = b₁(du/dt) + b₀u
↓ 拉普拉斯变换
代数方程: (a₁s + a₀)Y(s) = (b₁s + b₀)U(s)
↓ 整理
b₁s + b₀ b₁(s + b₀/b₁) s + z
G(s) = ─────────── = ───────────────── = ─────
a₁s + a₀ a₁(s + a₀/a₁) s + p- 分母的根(极点):来自系统本身的动力学特性(质量、弹簧、阻尼等)
- 分子的根(零点):来自输入信号如何"注入"系统
3.3 零点与极点:系统命运的两只手
┌─────────────────────────────────────────────────────────────────────┐
│ 零点 vs 极点:角色分工 │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ ┌─────────────────────────────────────────────────────────────┐ │
│ │ 🎚️ 极点 (s = -p) │ │
│ │ ───────────────────────────────────────────────────────── │ │
│ │ • 决定系统的"固有模态"------系统自己会怎么振荡/衰减 │ │
│ │ • 相当于乐器的固有音色 │ │
│ │ • 极点位置决定响应的时间常数 τ = 1/p │ │
│ │ │ │
│ │ 类比:极点像房间的回声特性------你喊一声后房间怎么回响 │ │
│ └─────────────────────────────────────────────────────────────┘ │
│ │
│ ┌─────────────────────────────────────────────────────────────┐ │
│ │ 🎛️ 零点 (s = -z) │ │
│ │ ───────────────────────────────────────────────────────── │ │
│ │ • 调节各模态被"激励"的强度 │ │
│ │ • 相当于混音师调节各音轨的音量 │ │
│ │ • 零点可以抵消或增强某些极点的效果 │ │
│ │ │ │
│ │ 类比:零点像说话者的发声方式------同一房间,不同人声音不同 │ │
│ └─────────────────────────────────────────────────────────────┘ │
│ │
│ 预判系统行为 │
│ ┌────────────────────────┐ │
│ │ 极点在左半平面?→ 稳定 │ │
│ │ 极点在右半平面?→ 发散 │ │
│ │ 极点离虚轴远? → 响应快 │ │
│ │ 极点离虚轴近? → 响应慢 │ │
│ └────────────────────────┘ │
└─────────────────────────────────────────────────────────────────────┘4 零极点位置的魔法:z
p
4.1 频率响应视角:谁是老大?
┌─────────────────────────────────────────────────────────────────────┐
│ 传递函数的频率响应分析 │
│ │
│ G(jω) = (jω + z)/(jω + p) │
│ │
│ 幅值增益 |G| = √(ω² + z²) / √(ω² + p²) │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ 低频 (ω → 0):|G| ≈ z/p │
│ 高频 (ω → ∞):|G| ≈ 1 │
│ │
│ ═══════════════════════════════════════════════════════════════ │
│ │
│ 情况1:z < p (零点更靠近原点) │
│ ────────────────────────────── │
│ │
│ 增益 |G| │
│ ↑ │
│ 1 │ ●━━━━━━━━━━━━━━━ │
│ │ ╱ │
│ │ ╱ │
│ z/p │━━━━━━━●╱ 低频增益 < 高频增益 │
│ │ → 高通特性 → 微分器 │
│ └────────────────────────────▶ ω │
│ │
│ 情况2:z > p (极点更靠近原点) │
│ ────────────────────────────── │
│ │
│ 增益 |G| │
│ ↑ │
│ z/p │━━━━━━━● │
│ │ ╲ │
│ │ ╲ 低频增益 > 高频增益 │
│ 1 │ ╲●━━━━━━━━━━━━━━━ │
│ │ → 低通特性 → 积分器 │
│ └────────────────────────────▶ ω │
│ │
└─────────────────────────────────────────────────────────────────────┘4.2 生活类比:水库与瀑布
┌─────────────────────────────────────────────────────────────────────┐
│ │
│ 【z < p:微分特性】------像瀑布边缘的探测器 │
│ ═══════════════════════════════════════ │
│ │
│ 水量突然增大 │
│ ↓ │
│ ╔═══════╗ │
│ ~~~║ ║ │
│ ~~~~║ ║↓↓↓↓ │
│ ~~~~~║ ║↓↓↓↓ │
│ ╚═══════╝ │
│ │ │
│ 探测器读数 │
│ │
│ 瀑布水流探测器: │
│ • 水量变化快时(高频)→ 响应强烈,水花四溅 │
│ • 水量稳定时(低频)→ 响应平淡 │
│ • 对"变化率"敏感 = 微分特性 │
│ │
│ 实际例子:速度传感器、涡流式流量计 │
│ │
└─────────────────────────────────────────────────────────────────────┘
┌─────────────────────────────────────────────────────────────────────┐
│ │
│ 【z > p:积分特性】------像水库的蓄水池 │
│ ═══════════════════════════════════════ │
│ │
│ 进水管 │
│ ↓↓↓ │
│ ┌─────────────┐ │
│ │ ~~~~~ │ ← 水位慢慢上升 │
│ │ ~~~~~ │ │
│ │ ~~~~~ │ │
│ │ ~~~~~ │ │
│ │ │ │
│ └─────────────┘ │
│ 水库 │
│ │
│ 水库蓄水系统: │
│ • 持续小流量(低频)→ 长期积累,水位显著升高 │
│ • 短暂大流量(高频)→ 来不及积累,影响不大 │
│ • 对"累积量"敏感 = 积分特性 │
│ │
│ 实际例子:电容充电、热量积累、银行存款 │
│ │
└─────────────────────────────────────────────────────────────────────┘4.3 阶跃响应的直观理解
┌─────────────────────────────────────────────────────────────────────┐
│ 对阶跃输入的响应对比 │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ 输入:突然从0跳到1(像突然打开水龙头) │
│ │
│ 【z < p:微分特性】 【z > p:积分特性】 │
│ │
│ y(t) y(t) │
│ ↑ ↑ │
│ 1 │● z/p│ ●━━━━━━━━ │
│ │ ╲ │ ╱ │
│ │ ╲ │ ╱ │
│ z/p │ ╲━━━━━━━━━━ 1 │ ╱ │
│ │ │● │
│ └───────────────▶ t └───────────────▶ t │
│ │
│ "急刹车型": "慢起步型": │
│ 初始跳跃大(感知到变化) 初始较低 │
│ 然后快速衰减到稳态 慢慢积累到更高稳态 │
│ │
│ 类比:猫见到黄瓜跳起来 类比:温水煮青蛙 │
│ (对突变敏感) (对缓变敏感) │
│ │
└─────────────────────────────────────────────────────────────────────┘5 时域 vs 复频域:两套思维工具
5.1 状态方程:时域的"逐帧分析"
┌─────────────────────────────────────────────────────────────────────┐
│ 状态方程方法 │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ dx/dt = Ax + Bu (状态方程) │
│ y = Cx + Du (输出方程) │
│ │
│ ┌─────────────────────────────────────────────────────────────┐ │
│ │ │ │
│ │ x₁(t)──▶● │ │
│ │ ╲ │ │
│ │ x₂(t)────●──▶ 系统内部状态 ──▶ 输出 y(t) │ │
│ │ ╱ "正在发生什么" │ │
│ │ x₃(t)──▶● │ │
│ │ │ │
│ └─────────────────────────────────────────────────────────────┘ │
│ │
│ 特点: │
│ • 直接追踪系统内部每个变量随时间的演化 │
│ • 就像电影的逐帧播放,能看到完整过程 │
│ • 可以处理非零初始条件、非线性、时变系统 │
│ │
└─────────────────────────────────────────────────────────────────────┘5.2 两种方法的对比
┌─────────────────────────────────────────────────────────────────────┐
│ 状态方程(时域) vs 传递函数(复频域) │
├─────────────────────────┬───────────────────────────────────────────┤
│ 状态方程方法 │ 传递函数方法 │
│ (内科医生) │ (体检报告) │
├─────────────────────────┼───────────────────────────────────────────┤
│ │ │
│ 👁️ 能看到什么: │ 👁️ 能看到什么: │
│ 系统内部所有状态变量 │ 只看输入→输出的关系 │
│ "心肝脾肺肾都看得见" │ "只看最终体检指标" │
│ │ │
│ 📊 处理对象: │ 📊 处理对象: │
│ 向量、矩阵运算 │ 多项式、分式运算 │
│ │ │
│ 🔧 擅长场景: │ 🔧 擅长场景: │
│ • 多输入多输出(MIMO) │ • 单输入单输出(SISO) │
│ • 有初始条件的问题 │ • 分析稳定性、频率特性 │
│ • 非线性系统分析 │ • 控制器设计(根轨迹、频域法) │
│ • 现代控制理论 │ • 经典控制理论 │
│ │ │
│ ⚡ 计算复杂度: │ ⚡ 计算复杂度: │
│ 需要数值积分 │ 代数运算,可求解析解 │
│ │ │
├─────────────────────────┴───────────────────────────────────────────┤
│ │
│ 🔗 它们的关系:传递函数是状态方程在"初始条件为零"时的输入输出映射 │
│ G(s) = C(sI - A)⁻¹B + D │
│ │
└─────────────────────────────────────────────────────────────────────┘5.3 平衡点:系统的"舒适区"
┌─────────────────────────────────────────────────────────────────────┐
│ 平衡点的物理意义 │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ 定义:dx/dt = 0 的点,即系统"静止"的状态 │
│ │
│ ┌───────────────────────────────────────────────────────────┐ │
│ │ │ │
│ │ 山谷底部 ← 稳定平衡点(小球会回来) │ │
│ │ ╱╲ │ │
│ │ ╱ ╲ │ │
│ │ ● ● │ │
│ │ ╱ ╲ │ │
│ │ ╱ ╲ 山顶 ← 不稳定平衡点 │ │
│ │ ╱ ╲ (小球一推就滚走) │ │
│ │ ╱ ● ╲ │ │
│ └───────────────────────────────────────────────────────────┘ │
│ │
│ 与极点的关系: │
│ ━━━━━━━━━━━━━━ │
│ │
│ 在平衡点处线性化:dx/dt = A·Δx │
│ 矩阵A的特征值 = 该平衡点附近的极点 │
│ │
│ ┌────────────────────────────────────────────────────────┐ │
│ │ 极点全在左半平面 (Re < 0) → 平衡点稳定(山谷) │ │
│ │ 有极点在右半平面 (Re > 0) → 平衡点不稳定(山顶) │ │
│ │ 极点在虚轴上 → 临界稳定(山脊) │ │
│ └────────────────────────────────────────────────────────┘ │
│ │
└─────────────────────────────────────────────────────────────────────┘6 完整认知框架:一张地图
┌─────────────────────────────────────────────────────────────────────┐
│ 控制理论认知框架总览 │
├─────────────────────────────────────────────────────────────────────┤
│ │
│ ╔═══════════════════════════════════════════════════════════════╗ │
│ ║ 物理世界 ║ │
│ ║ ┌──────────┐ ┌──────────┐ ┌──────────┐ ║ │
│ ║ │ 输入 │ ───▶ │ 系统 │ ───▶ │ 输出 │ ║ │
│ ║ │ u(t) │ │(微分方程) │ │ y(t) │ ║ │
│ ║ └──────────┘ └──────────┘ └──────────┘ ║ │
│ ╚═══════════════════════════════════════════════════════════════╝ │
│ ↓ │
│ ┌────────────────────┴────────────────────┐ │
│ ↓ ↓ │
│ ┏━━━━━━━━━━━━━━━━━━━┓ ┏━━━━━━━━━━━━━━━━━━━━┓ │
│ ┃ 时域分析 ┃ ┃ 复频域分析 ┃ │
│ ┃ (状态方程) ┃ ◀═══▶ ┃ (传递函数) ┃ │
│ ┃ ┃ 拉普拉斯 ┃ ┃ │
│ ┃ dx/dt = Ax + Bu ┃ 变换 ┃ G(s) = Y(s)/U(s) ┃ │
│ ┃ ┃ ┃ ┃ │
│ ┃ • 看内部状态 ┃ ┃ • 看输入输出 ┃ │
│ ┃ • 矩阵特征值 ┃ ┃ • 零点和极点 ┃ │
│ ┃ • 平衡点分析 ┃ ┃ • 频率响应 ┃ │
│ ┗━━━━━━━━━━━━━━━━━━━┛ ┗━━━━━━━━━━━━━━━━━━━━┛ │
│ │ │ │
│ ↓ ↓ │
│ ┌──────────────────┐ ┌──────────────────────┐ │
│ │ 特征值 = 极点 │ ◀═══════════▶ │ 极点决定固有模态 │ │
│ │ 决定稳定性 │ │ 零点调节模态权重 │ │
│ └──────────────────┘ └──────────────────────┘ │
│ │
│ ┌────────────────────┐ │
│ │ 设计控制器 │ │
│ │ 调整零极点位置 │ │
│ │ 达到期望性能 │ │
│ └────────────────────┘ │
│ │
└─────────────────────────────────────────────────────────────────────┘7 超前校正与滞后校正:给系统"吃药"
如果系统表现不完美,我们需要给它加个滤镜(校正器)。
- 超前校正 (Lead):给系统喝杯咖啡。
- 原理: 利用微分特性,预测未来的趋势。
- 作用: 让系统反应变快,增加系统的"敏捷度",就像让一个迟钝的人变得机灵,提前预判动作。
- 滞后校正 (Lag):给系统吃片镇静剂。
- 原理: 利用积分特性,积累过去的信号,把高频噪声滤掉。
- 作用: 牺牲一点反应速度,换取更高的稳态精度。就像让一个毛躁的人沉稳下来,虽然慢点,但干活细致,误差小。
7.1 问题的提出
┌─────────────────────────────────────────────────────────────────────────────────┐
│ 控制系统的两难困境 │
├─────────────────────────────────────────────────────────────────────────────────┤
│ │
│ 场景:你在调节淋浴水温 │
│ │
│ 困境1:反应太慢 │
│ ┌─────────────────────────────────────────────────┐ │
│ │ 你:好冷!大幅拧热水 │ │
│ │ 系统:(2秒后) 好烫! │ │
│ │ 你:大幅拧冷水 │ │
│ │ 系统:(2秒后) 好冷! │ │
│ │ ... 永远在冷热之间震荡 ... │ │
│ └─────────────────────────────────────────────────┘ │
│ 问题:系统响应慢(相位滞后),导致你的控制总是"过时" │
│ │
│ 困境2:反应太激进 │
│ ┌─────────────────────────────────────────────────┐ │
│ │ 你:稍微有点冷,轻轻拧一下 │ │
│ │ 系统:疯狂输出热水 │ │
│ │ 结果:剧烈振荡 │ │
│ └─────────────────────────────────────────────────┘ │
│ 问题:增益太高,系统不稳定 │
│ │
│ 工程师的智慧:能不能在控制器中"预判"或"平滑"信号,来解决这些问题? │
│ │
└─────────────────────────────────────────────────────────────────────────────────┘7.2 超前校正:预判大师
┌─────────────────────────────────────────────────────────────────────────────────┐
│ 超前校正 (Lead Compensation) │
├─────────────────────────────────────────────────────────────────────────────────┤
│ │
│ 核心思想:让控制信号"提前行动" │
│ │
│ ┌─────────────────────────────────────────────────────────────────────────┐ │
│ │ │ │
│ │ 原始信号 │ │
│ │ ──────╱╲ │ │
│ │ ╱ ╲ │ │
│ │ ╱ ╲────── │ │
│ │ │ │
│ │ ↓ 超前校正器 │ │
│ │ │ │
│ │ 超前后的信号 │ │
│ │ ────╱╲ (信号被"提前"了) │ │
│ │ ╱ ╲ │ │
│ │ ╱ ╲────── │ │
│ │ │ │
│ └─────────────────────────────────────────────────────────────────────────┘ │
│ │
│ 传递函数形式: │
│ s + z │
│ G_lead(s) = ──────── 其中 z < p (零点在极点左边) │
│ s + p │
│ │
│ 物理意义: │
│ - 对高频信号放大更多 → 强调"变化趋势" │
│ - 相当于在PID中加强D(微分)的作用 │
│ - 让系统"预见"未来,提前动作 │
│ │
│ 生活比喻: │
│ 开车看到远处有弯道 → 提前打方向盘,而不是到了弯道才打 │
│ │
│ 适用场景: │
│ ✓ 系统响应慢,需要加快 │
│ ✓ 相位裕度不够,需要增加稳定性 │
│ ✓ 需要减小超调 │
│ │
│ 代价:放大高频噪声 │
│ │
└─────────────────────────────────────────────────────────────────────────────────┘7.3 滞后校正:平滑大师
┌─────────────────────────────────────────────────────────────────────────────────┐
│ 滞后校正 (Lag Compensation) │
├─────────────────────────────────────────────────────────────────────────────────┤
│ │
│ 核心思想:低频增益大,高频增益小 → "平滑"控制动作 │
│ │
│ ┌─────────────────────────────────────────────────────────────────────────┐ │
│ │ │ │
│ │ 增益 │ │
│ │ │ │ │
│ │ 高 │ ████ │ │
│ │ │ ████████ │ │
│ │ 低 │ ████████████████ │ │
│ │ └──────────────────────▶ 频率 │ │
│ │ 低频 高频 │ │
│ │ │ │
│ │ 低频(稳态)增益高 → 消除稳态误差 │ │
│ │ 高频(快变)增益低 → 抑制噪声和振荡 │ │
│ │ │ │
│ └─────────────────────────────────────────────────────────────────────────┘ │
│ │
│ 传递函数形式: │
│ s + z │
│ G_lag(s) = ──────── 其中 z > p (零点在极点右边) │
│ s + p │
│ │
│ 物理意义: │
│ - 相当于在PID中加强I(积分)的作用 │
│ - 让系统"更有耐心",不急于响应快速变化 │
│ │
│ 生活比喻: │
│ 老中医看病 → 不急于下药,先观察一段时间再决定 │
│ │
│ 适用场景: │
│ ✓ 需要消除稳态误差 │
│ ✓ 系统有高频噪声需要滤除 │
│ ✓ 增益足够但稳态精度不够 │
│ │
│ 代价:响应变慢 │
│ │
└─────────────────────────────────────────────────────────────────────────────────┘7.4 超前滞后对比
┌─────────────────────────────────────────────────────────────────────────────────┐
│ 超前 vs 滞后 校正对比 │
├─────────────────────────────────────────────────────────────────────────────────┤
│ │
│ 超前校正 滞后校正 │
│ ┌──────────────────────────┐ ┌──────────────────────────┐ │
│ │ 🏎️ "赛车手" │ │ 🐢 "老司机" │ │
│ │ │ │ │ │
│ │ • 反应快 │ │ • 稳态准 │ │
│ │ • 预判趋势 │ │ • 滤除噪声 │ │
│ │ • 减小超调 │ │ • 响应平滑 │ │
│ │ │ │ │ │
│ │ 代价: 噪声敏感 │ │ 代价: 响应慢 │ │
│ └──────────────────────────┘ └──────────────────────────┘ │
│ │
│ ═══════════════════════════════════════════════════════════════════════════ │
│ │
│ 实际工程中常常组合使用:超前-滞后校正器 │
│ │
│ s + z₁ s + z₂ │
│ G = ─────── · ─────── z₁ < p₁ ; z₂ > p₂ │
│ s + p₁ s + p₂ │
│ 超前 滞后 │
│ │
│ 既要快速响应,又要稳态精度 → 两者结合! │
│ │
└─────────────────────────────────────────────────────────────────────────────────┘7.5 关键记忆口诀
┌─────────────────────────────────────────────────────────────────────┐
│ │
│ 拉普拉斯变换:微分变乘法,积分变除法,解方程不再怕 │
│ │
│ 2. 复频率 s = σ + jω:σ管生死(衰减/增长),ω管振荡快慢 │
│ │
│ 3. 传递函数:分子是零点(调音量),分母是极点(定音色) │
│ │
│ 4. 极点定命运:左半平面稳,右半平面炸,离虚轴越远响应越快 │
│ │
│ 5. 零极点相对位置:z<p像微分(敏感变化),z>p像积分(累积效应) │
│ │
│ 6. 两种方法:状态方程看内部电影,传递函数看外部效果 │
│ │
└─────────────────────────────────────────────────────────────────────┘