一、线性代数最重要的结论你认为是什么?
这是一个非常深刻的问题。如果非要从线性代数浩瀚的定理中挑选一个 "皇冠上的明珠" ,我会认为是:线性变换的矩阵表示 (The Representation of Linear Transformations by Matrices)
简单来说,这个结论告诉我们:所有的线性变换都可以用矩阵来描述,而所有的矩阵都代表着某种空间变换。
1. 为什么它是最重要的?
线性代数不仅仅是关于解方程组(那是初等阶段),它本质上是研究向量空间之间的映射。这个结论建立了一座桥梁:
- 几何直觉: 线性变换(旋转、缩放、投影、剪切)。
- 代数运算: 矩阵乘法、特征值、行列式。
如果没有这个结论,矩阵就只是一堆死板的数字;有了它,矩阵就变成了**"动作"**。当你看到矩阵 AAA 乘以向量 x\mathbf{x}x 时,你不应该只想到一堆加法和乘法,而应该看到向量 x\mathbf{x}x 在空间中被移动到了一个新的位置。
2. 这个结论延伸出的三个"终极洞察"
如果沿着这个逻辑往下走,你会发现线性代数的核心其实都在解释这一件事:
- 矩阵分解(如 SVD 分解): 任何复杂的动作(矩阵),都可以拆解为"旋转-缩放-旋转"三个简单的动作。这是现代图像压缩和推荐算法的数学基石。
- 特征值与特征向量 (Av=λvA\mathbf{v} = \lambda\mathbf{v}Av=λv): 在线性变换的混乱中,是否存在某些方向,向量在这个方向上只发生缩放而不改变方向?这些方向就是变换的"灵魂"。
- 基变换 (Change of Basis): 同样的变换,在不同的观察者(基)眼里,矩阵的复杂度完全不同。对角化矩阵就是找到了一个最完美的观察视角。
3. 现实世界的意义
正因为我们可以用矩阵来表示变换,计算机才得以通过高效的并行计算(GPU)来处理:
- 3D 游戏渲染:每一帧画面的旋转和透视都是矩阵变换。
- 深度学习:神经网络本质上就是无数个高维空间中的线性变换叠加非线性激活函数。
- 量子力学:物理系统的演化被描述为希尔伯特空间中的线性算子(算子本质上就是无限维的矩阵)。
线性变换与矩阵的等价性之所以是最重要的,因为它赋予了代数以几何的灵魂。它让我们明白:数学不是在玩数字游戏,而是在描述空间的结构和演变。
二、奇异值分解(SVD)
2.1 推导过程
推导奇异值分解(SVD)最直观的方法,是基于以上讨论的核心观点:矩阵代表一种空间变换。
既然任何矩阵 AAA 都是一种变换,我们可以从"这个变换对空间做了什么"入手。推导过程主要分为三步:
第一步:寻找"诚实"的方向
假设 AAA 是一个 m×nm \times nm×n 的矩阵。它把 nnn 维空间中的向量映射到 mmm 维空间。我们想在原空间(输入空间)中找一组相互垂直的单位向量 {v1,v2,...,vn}\{v_1, v_2, \dots, v_n\}{v1,v2,...,vn},使得它们经过 AAA 变换后,在目标空间中仍然是相互垂直的。
虽然一般的向量变换后会"扭曲",但线性代数告诉我们,对称矩阵总是可以对角化的。于是我们构造一个对称矩阵:ATAA^T AATA这是一个 n×nn \times nn×n 的实对称矩阵。根据谱定理(Spectral Theorem),它一定有一组正交单位特征向量 {v1,v2,...,vn}\{v_1, v_2, \dots, v_n\}{v1,v2,...,vn},对应的特征值为 λ1,λ2,...,λn\lambda_1, \lambda_2, \dots, \lambda_nλ1,λ2,...,λn(且均为非负实数)。
第二步:观察变换后的样子
我们将这些特征向量通过 AAA 进行变换,得到一组新向量 ui′=Aviu'_i = A v_iui′=Avi。来看看它们的内积:(Avi)⋅(Avj)=(Avi)T(Avj)=viT(ATA)vj(A v_i) \cdot (A v_j) = (A v_i)^T (A v_j) = v_i^T (A^T A) v_j(Avi)⋅(Avj)=(Avi)T(Avj)=viT(ATA)vj因为 vjv_jvj 是 ATAA^T AATA 的特征向量,所以 (ATA)vj=λjvj(A^T A) v_j = \lambda_j v_j(ATA)vj=λjvj:viT(λjvj)=λj(viTvj)v_i^T (\lambda_j v_j) = \lambda_j (v_i^T v_j)viT(λjvj)=λj(viTvj)由于 viv_ivi 是正交的:
- 当 i≠ji \neq ji=j 时,内积为 000。这意味着变换后的向量 AviAv_iAvi 和 AvjAv_jAvj 依然保持垂直。
- 当 i=ji = ji=j 时,内积为 λi\lambda_iλi。这意味着变换后向量的长度平方为 λi\lambda_iλi。
我们令奇异值 σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi 。如果 σi>0\sigma_i > 0σi>0,我们定义单位向量:ui=Aviσiu_i = \frac{A v_i}{\sigma_i}ui=σiAvi
第三步:写成矩阵形式
现在我们有了:
- V=[v1,v2,...,vn]V = [v_1, v_2, \dots, v_n]V=[v1,v2,...,vn](输入空间的垂直基底,即旋转/反射)
- Σ\SigmaΣ 是对角矩阵,对角线上是 σi\sigma_iσi(拉伸/缩放)
- U=[u1,u2,...,um]U = [u_1, u_2, \dots, u_m]U=[u1,u2,...,um](目标空间的垂直基底,即旋转/反射)
根据 Avi=σiuiA v_i = \sigma_i u_iAvi=σiui,写成矩阵拼接的形式就是:AV=UΣA V = U \SigmaAV=UΣ由于 VVV 是正交矩阵(V−1=VTV^{-1} = V^TV−1=VT),两边同时右乘 VTV^TVT:A=UΣVTA = U \Sigma V^TA=UΣVT
总结 SVD 的物理意义
这个推导过程完美解释了 SVD 的本质:任何矩阵变换 AAA 都可以分解为三个简单的步骤:
- VTV^TVT (旋转):在原空间旋转,把坐标系对准那些变换后不会扭曲的方向。
- Σ\SigmaΣ (缩放):在这些特定的方向上进行拉伸或压缩,拉伸幅度就是奇异值。
- UUU (旋转):在目标空间再次旋转,调整到最终的姿态。
为什么它比特征值分解更强大? 特征值分解要求矩阵必须是方阵,且必须有足够的特征向量;而 SVD 的推导利用了 ATAA^TAATA 的对称性,对任何形状的矩阵(长方形、正方形)都成立。这也就是为什么在数据降维(PCA)和信号处理中,SVD 才是真正的"终极工具"。
2.2 一个小疑问:vvv有nnn个,uuu有mmm个,多余的u去哪了?
这个问题触及了线性代数中最核心的几何关系:秩(Rank)、值域(Range)和零空间(Nullspace)。
简单来说:多余的 uuu 并没有消失,它们构成了目标空间里那些" AAA 无法到达的地方"。
为了理解透彻,我们分两种情况来看:
1. 如果 m>nm > nm>n(矩阵是"瘦长型")
这意味着你把一个低维空间的向量映射到了高维空间(比如把一张 2D 照片贴到 3D 房间的墙上)。
- u1u_1u1 到 unu_nun:这些向量是 AAA 的值域基底。它们对应着输入空间里那 nnn 个 vvv 向量变换后的位置。
- 多余的 un+1u_{n+1}un+1 到 umu_mum:这些向量是目标空间里与 AAA 的值域正交的部分。
- 几何直觉:如果你把 2D 平面映射到 3D 空间,你会得到一个平面。那些"多余的 uuu"就是垂直于这个平面的法向量。
- 它们的奇异值:在 Σ\SigmaΣ 矩阵中,对应的位置全是 0。这代表原空间中没有任何能量能转化到这些维度上。
2. 核心结论:SVD 实际上划分了空间
完备的 SVD 公式 A=UΣVTA = U\Sigma V^TA=UΣVT 其实是把两个空间都彻底"拆解"了:
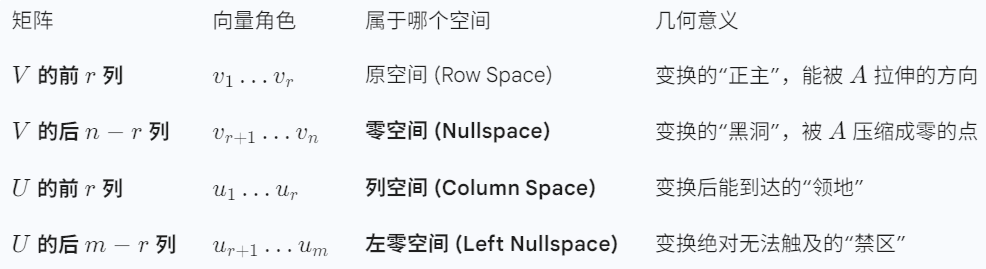
注:这里 rrr 是矩阵的秩(Rank),即非零奇异值的个数。
3. "多余"的 uuu 有什么用?
既然 AAA 永远无法到达多余的 uuu 所代表的方向,那为什么还要写出它们?这是为了满足正交基 的完备性。虽然 AAA 无法直接映射到这些方向,但在处理最小二乘法 或线性方程组无解 的情况时,这些多余的 uuu 极其关键:
- 它们定义了残差(Residual)。
- 当你想找一个最接近的解时,你会发现误差向量正好就落在这些"多余"的 uuu 所张成的空间里。
多余的 uuu 是为了凑齐 mmm 维空间的"导航手册"。
- vvv 侧:多余的 vvv 是被 AAA 吞噬掉的维度(变成 0)。
- uuu 侧:多余的 uuu 是 AAA 够不到的维度。这就是为什么 SVD 被称为"全能分解",因为它不仅告诉了你矩阵能做什么(前 rrr 个向量),还清晰地标出了矩阵做不到什么(剩下的向量)。
2.3 如何用SVD来做图像压缩?
SVD如何神奇地将一张大照片"瘦身"成小照片,同时保持大部分视觉信息?这就是低秩逼近(Low-Rank Approximation) 在图像压缩中的应用。
1. 照片的数学表示
一张灰度图片可以看作一个巨大的二维矩阵 AAA。每个元素 AijA_{ij}Aij 代表像素点 (i,j)(i,j)(i,j) 的灰度值(通常在 0 到 255 之间)。一张彩色图片则通常由红、绿、蓝(RGB)三个通道组成,每个通道都是一个灰度矩阵。
比如,一张 1000x1000 像素的灰度图片,就是一个 1000×10001000 \times 10001000×1000 的矩阵。直接存储需要 100 万个数字。
2. SVD 的完全分解
我们知道,任何矩阵 AAA 都可以进行 SVD 分解:A=UΣVTA = U \Sigma V^TA=UΣVT其中:
- UUU 是一个 m×mm \times mm×m 的正交矩阵。
- Σ\SigmaΣ 是一个 m×nm \times nm×n 的对角矩阵,对角线上的元素是奇异值 σ1≥σ2≥⋯≥σr>0\sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_r > 0σ1≥σ2≥⋯≥σr>0,后面都是 0。
- VTV^TVT 是一个 n×nn \times nn×n 的正交矩阵。
这个公式可以进一步写成 "外积和" 的形式:A=∑i=1rσiuiviTA = \sum_{i=1}^r \sigma_i u_i v_i^TA=i=1∑rσiuiviT这里,uiu_iui 是 UUU 的第 iii 列(一个 m×1m \times 1m×1 的向量),viTv_i^TviT 是 VTV^TVT 的第 iii 行(一个 1×n1 \times n1×n 的向量)。每一个 uiviTu_i v_i^TuiviT 都是一个秩为 1 的矩阵**,σi\sigma_iσi 是对应的权重。
这意味着原图 AAA 可以看作是 rrr 个"基本图像"(秩为 1 的矩阵)的加权和。
3. 低秩逼近:只取最重要的信息
关键在于奇异值 σi\sigma_iσi 的排序:它们是从大到小排列的。
- 大的奇异值 对应的 uiviTu_i v_i^TuiviT 项捕捉了图片中最重要的、能量最高的信息(比如边缘、大块区域的颜色)。
- 小的奇异值 对应的项通常包含的是细节、噪声,或者那些对整体视觉影响不大的信息。
低秩逼近的核心思想是:我们不需要所有的 rrr 项。我们只需要选取前 kkk 个最大的奇异值及其对应的 uiu_iui 和 viTv_i^TviT 。Ak=∑i=1kσiuiviTA_k = \sum_{i=1}^k \sigma_i u_i v_i^TAk=i=1∑kσiuiviT其中 k≪rk \ll rk≪r。这个 AkA_kAk 就是原图 AAA 的秩为 kkk 的最佳逼近(在 Frobenius 范数意义下)。
4. 压缩效果
我们来计算一下存储的数据量:
- 原始图片 AAA: m×nm \times nm×n 个数字。
- 低秩逼近 AkA_kAk:需要存储 kkk 个奇异值 σi\sigma_iσi,kkk 个 uiu_iui 向量(每个 mmm 个数字),和 kkk 个 viTv_i^TviT 向量(每个 nnn 个数字)。
- 总存储量:k⋅1k \cdot 1k⋅1 (for σi\sigma_iσi) +k⋅m+ k \cdot m+k⋅m (for uiu_iui) +k⋅n+ k \cdot n+k⋅n (for viTv_i^TviT) =k(1+m+n)= k(1 + m + n)=k(1+m+n) 个数字。
举例:1000x1000 的灰度图片 (m=n=1000m=n=1000m=n=1000)
- 原始存储:1000×1000=1,000,0001000 \times 1000 = 1,000,0001000×1000=1,000,000 个数字。
- 如果我们取前 k=50k=50k=50 个奇异值:
- 存储量:50×(1+1000+1000)≈50×2000=100,00050 \times (1 + 1000 + 1000) \approx 50 \times 2000 = 100,00050×(1+1000+1000)≈50×2000=100,000 个数字。
- 压缩比达到 10:1!
对于彩色图片,对每个 R, G, B 通道分别进行 SVD 压缩,再组合起来。