RL4LLM - 技术栈

RL4LLM

这是新的学习方向，已经抛弃了rec(^_）。

具体的学习资源推荐（包括必学资源、选学资源）、项目实践清单，见学习路径文档。

Claude说：在LLM时代，工程能力>理论深度。并且要"代码驱动学习"。

python 复制代码

 # 不要这样学
 理论 → 推导 → 代码 → 应用
 
 # 应该这样学
 跑通代码 → 理解输入输出 → 回头补理论 → 改进代码

能跑通并改进开源项目 > 会推导公式

理解工程trade-off > 追求理论完美

快速学习新技术 > 系统掌握旧知识

"不要等到'准备好了'再开始!"

文章目录

第一阶段：快速入门（2-4周）
- [1. 最小必要的ML基础（1周）](#1. 最小必要的ML基础（1周）)
- [2. 深度学习速成（1周）](#2. 深度学习速成（1周）)
- [3. Transformer与LLM基础（2周）](#3. Transformer与LLM基础（2周）)
第二阶段：LLM核心技术（4-6周）
- [1. LLM预训练与微调](#1. LLM预训练与微调)
- [2. 提示工程与上下文学习](#2. 提示工程与上下文学习)
- [3. 强化学习预备知识](#3. 强化学习预备知识)
第三阶段：LLM强化学习深入（6-8周）

第一阶段：快速入门（2-4周）

1. 最小必要的ML基础（1周）

梯度下降、反向传播
过拟合/欠拟合
损失函数基本概念
简单实现一个线性回归/逻辑回归

1.1梯度下降

梯度是一个向量，由函数对所有参数的偏导数组成。

对于参数向量 θ = [ θ 1 , θ 2 , . . , θ n ] T \theta =\left[ \theta _1,\theta _2,..,\theta _n \right] ^T θ=[θ1,θ2,..,θn]T，梯度的定义：
∇ J ( θ ) = [ ∂ J ∂ θ 1 , ∂ J ∂ θ 2 , . . . , ∂ J ∂ θ n ] T \nabla J\left( \theta \right) =\left[ \frac{\partial J}{\partial \theta _1},\frac{\partial J}{\partial \theta _2},...,\frac{\partial J}{\partial \theta _n} \right] ^T ∇J(θ)=[∂θ1∂J,∂θ2∂J,...,∂θn∂J]T

梯度向量的方向是函数值上升最快的方向，因此负梯度方向就是函数值下降最快的方向------ 这是梯度下降算法的核心理论依据。

在机器学习中，我们的目标是找到一组参数 θ θ θ，使得损失函数 J ( θ ) J(θ) J(θ) 达到最小值（全局最小值或局部最小值）。贪心，每一步都选择当前最优的下降方向。

1.从一个初始参数 θ0 出发；

2.沿着损失函数的负梯度方向不断更新参数；

3.每次更新都使损失函数 J(θ) 尽可能减小；

4.当损失函数收敛到稳定值（或参数变化量小于阈值）时，停止更新，此时的参数 θ 即为最优参数。

数学推导

梯度下降算法（批量梯度下降）

输入：

损失函数 J ( θ ) J(\theta) J(θ)
梯度函数 ∇ J ( θ ) \nabla J(\theta) ∇J(θ)
学习率 α \alpha α
收敛阈值 ϵ \epsilon ϵ
最大迭代次数 T T T

输出：最优参数 θ ∗ \theta^* θ∗

算法步骤：

初始化参数： θ = 随机值或全零向量 \theta = \text{随机值或全零向量} θ=随机值或全零向量
遍历迭代（ t = 1 → T t = 1 \to T t=1→T）：
3. 计算当前梯度： g = ∇ J ( θ ) g = \nabla J(\theta) g=∇J(θ)
4. 更新参数： θ = θ − α ⋅ g \theta = \theta - \alpha \cdot g θ=θ−α⋅g
5. 计算当前损失： J t = J ( θ ) J_t = J(\theta) Jt=J(θ)
6. 收敛判断：若 ∣ J t − J t − 1 ∣ < ϵ |J_t - J_{t-1}| < \epsilon ∣Jt−Jt−1∣<ϵ 或 ∣ ∣ g ∣ ∣ < ϵ ||g|| < \epsilon ∣∣g∣∣<ϵ，则跳出迭代
返回最优参数 θ \theta θ

超参数（学习率、批量大小【批量大小决定了计算梯度时使用的样本数量】）

1.2反向传播

图片来自：
5分钟-通俗易懂 - 神经网络反向传播算法（手算）
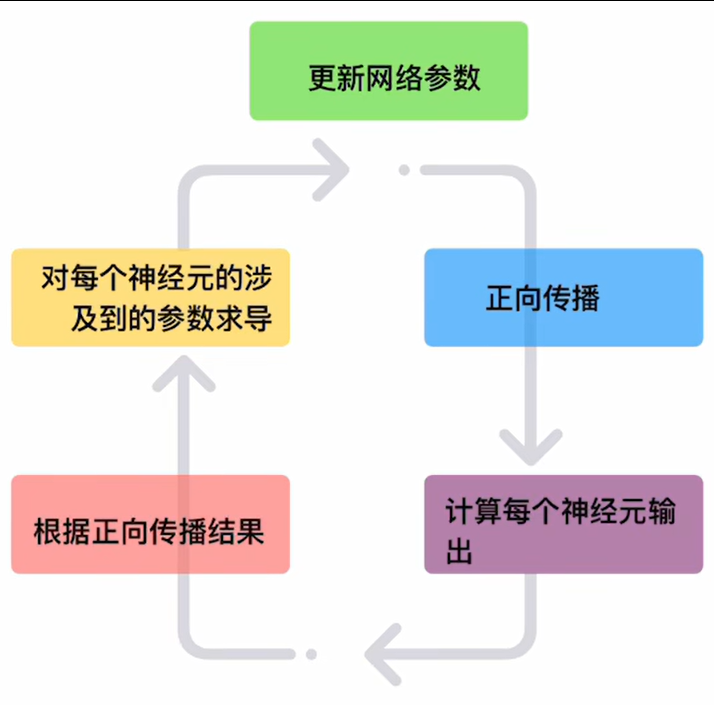更新网络参数也是用的梯度下降思想。

反向传播就是链式法则的递归应用，去展开下面的式子： ∂ f l o s s ∂ 神经元参数 \frac{\partial f_{loss}}{\partial \text{神经元参数}} ∂神经元参数∂floss

复习链式法则：

对于复合函数 y = f ( u ) y=f(u) y=f(u), u = g ( x ) u=g(x) u=g(x)，有：
d y d x = d y d u ⋅ d u d x \frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx} dxdy=dudy⋅dxdu
对于多变量情况（如 L = f ( a , b ) L=f(a,b) L=f(a,b), a = g ( w ) a=g(w) a=g(w), b = h ( w ) b=h(w) b=h(w)），则是偏导数的链式展开：
∂ L ∂ w = ∂ L ∂ a ⋅ ∂ a ∂ w + ∂ L ∂ b ⋅ ∂ b ∂ w \frac{\partial L}{\partial w}=\frac{\partial L}{\partial a}\cdot \frac{\partial a}{\partial w}+\frac{\partial L}{\partial b}\cdot \frac{\partial b}{\partial w} ∂w∂L=∂a∂L⋅∂w∂a+∂b∂L⋅∂w∂b

1.3过拟合/欠拟合

已经掌握

1.4损失函数基本概念

衡量预测值和真实值差异的函数。这里学习分类任务损失函数里的交叉熵损失（是模式识别与机器学习课程的考察内容）。

1.4.1二分类交叉熵损失

1.4.2多分类交叉熵损失

1.5动手实现线性回归

1.6动手实现逻辑回归

2. 深度学习速成（1周）

PyTorch基础操作
训练一个简单的CNN/RNN
理解attention机制

3. Transformer与LLM基础（2周）

Transformer架构
使用Hugging Face跑通GPT-2
理解tokenization、embedding

第二阶段：LLM核心技术（4-6周）

1. LLM预训练与微调

理解预训练目标（MLM、CLM）
动手微调一个小模型（如BERT-base）
了解LoRA、QLoRA等高效微调方法

2. 提示工程与上下文学习

Few-shot learning
Chain-of-thought
指令微调基础

3. 强化学习预备知识

RL基本概念（只需要1-2天）
策略梯度基础
价值函数概念

第三阶段：LLM强化学习深入（6-8周）

第1-2周：RLHF基础**

人类偏好建模
奖励模型训练
PPO在LLM中的应用

第3-4周：DPO及其变种**

DPO原理与实现
SimPO、IPO等新方法
对比不同方法的优缺点

第5-6周：实战项目**

基于TRL库实现完整RLHF pipeline
在小模型上复现DPO
参与开源项目（如LLaMA-Factory）

第7-8周：前沿技术**

DeepSeek R1的技术解读
GRPO等新方法
多模态RLHF