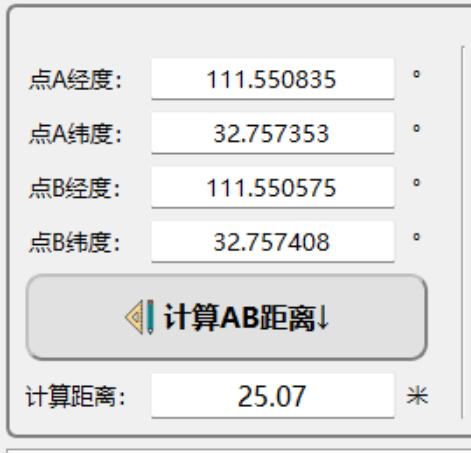
基于 Haversine 公式实现【经纬度坐标点】球面距离计算（C++/Qt 实现）

一、功能说明

本文实现的核心功能：输入两个地理坐标点 A (lat1,lon1)、B (lat2,lon2) 的十进制度 (DD 格式) 经纬度，通过经典的 Haversine 公式，计算两点间的地球球面直线距离 ，单位为米 (m)。

二、核心前置知识

✅ 坐标格式要求

本代码中计算使用的经纬度，必须为 DD 格式（十进制度），也是最适合程序计算的格式：

纬度范围：[-90.0, 90.0]，北纬为正，南纬为负；
经度范围：[-180.0, 180.0]，东经为正，西经为负。

若你的项目中只有 DMS 格式（度分秒），可通过「度分秒转十进制度」的转换逻辑预处理后，再代入本公式计算（我往期博客有完整的 DD/DMS 互转实现）。

✅ 为什么用 Haversine 公式？

地球是一个不规则的椭球体 ，日常开发中做近似计算时，均将地球视为完美球体 ，此时最经典、最高效的球面两点距离计算公式就是 Haversine 公式。

公式优势：计算逻辑简洁、运算量小、精度足够，误差在 1% 以内，能满足绝大多数场景（导航、GIS 开发、坐标测距、机器人定位等）的需求；
核心适用：近距离 / 中距离的球面距离计算，是地理开发的必备基础公式。

✅ 核心常量与转换规则

地球平均半径常量：R = 6371000.0 米 (6371km)，这是行业通用的地球半径取值，也是本代码的核心常量；
角度转弧度规则：程序中三角函数 (sin/cos/atan2) 的入参要求为弧度值 ，因此必须将十进制度的经纬度 × π/180 完成角度→弧度的转换。

三、Haversine 公式完整推导与核心公式

公式核心思想

计算球面上两点的最短球面距离（大圆距离），核心是通过两点的经纬度差值，结合球面三角几何关系推导得出。

完整计算公式（弧度制）

plaintext

复制代码

已知：两点坐标 A(lat1, lon1) 、 B(lat2, lon2) ，地球半径 R
步骤1：经纬度转弧度：所有角度值 × π/180
步骤2：计算纬度差 Δlat = lat2 - lat1 ，经度差 Δlon = lon2 - lon1
步骤3：核心公式计算中间值a
a = sin²(Δlat/2) + cos(lat1) × cos(lat2) × sin²(Δlon/2)
步骤4：计算圆心角c
c = 2 × atan2(√a , √(1-a))
步骤5：计算球面距离
distance = R × c

四、C++/Qt 实现代码

完整代码

cpp 复制代码

void MainWindow::on_CalculateAB_Distance_Button_clicked()
{
    // 1. 读取界面两个坐标点的DD格式经纬度
    double lat1 = ui->lineEdit_latA->text().toDouble();  // A点纬度
    double lon1 = ui->lineEdit_lonA->text().toDouble();  // A点经度
    double lat2 = ui->lineEdit_latB->text().toDouble();  // B点纬度
    double lon2 = ui->lineEdit_lonB->text().toDouble();  // B点经度

    // 2. 定义核心常量：地球平均半径(米)
    const double R = 6371000.0;

    // 3. 角度(十进制度) 转 弧度，三角函数必须传弧度值计算
    double lat1_rad = lat1 * M_PI / 180.0;
    double lon1_rad = lon1 * M_PI / 180.0;
    double lat2_rad = lat2 * M_PI / 180.0;
    double lon2_rad = lon2 * M_PI / 180.0;

    // 4. 计算经纬度的差值
    double dlat = lat2_rad - lat1_rad;
    double dlon = lon2_rad - lon1_rad;

    // 5. Haversine公式核心计算
    double a = sin(dlat / 2) * sin(dlat / 2) +
               cos(lat1_rad) * cos(lat2_rad) * sin(dlon / 2) * sin(dlon / 2);
    double c = 2 * atan2(sqrt(a), sqrt(1 - a));

    // 6. 计算最终球面距离(米)
    double distance = R * c;

    // 7. 结果赋值到界面显示
    ui->lineEdit_disAB->setText(QString::number(distance, 'f', 2));
}

界面效果：

补充：和往期博客联动

✅ 往期相关：经纬度坐标DD格式和DMS格式互转（十进制度-度分秒互转）