(一)人工智能算法之监督学习——KNN

一、KNN 算法核心原理

KNN（K-Nearest Neighbors，K 近邻）是最简单的机器学习算法之一，核心思想可以总结为："物以类聚，人以群分"。

1. 核心定义

对于一个待预测的样本，KNN 会在训练数据集中找到与它 "最相似"（距离最近）的 K 个样本，然后根据这 K 个样本的标签，通过 "投票" 的方式决定待预测样本的类别（分类任务），或取平均值作为预测值（回归任务）。

核心原理：待预测样本的类别（分类）或数值（回归），由特征空间中与它距离最近的 K 个训练样本（邻居）的信息决定。

核心假设：特征空间中相似的样本，其类别或数值也相近，用距离度量相似度，距离越小则相似度越高。

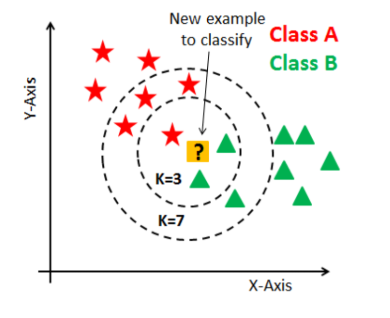
2. 算法执行步骤（以分类为例）

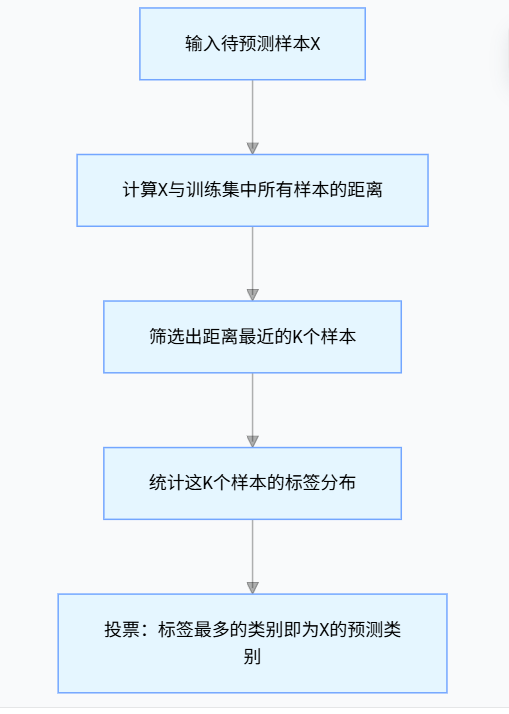
3.完整的算法步骤

1.设定超参数 K：人为设定参与决策的邻居数量，常见取 3、5、7 等奇数，避免二分类平局，最优 K 值常用交叉验证确定。

2.计算距离：用距离公式衡量待预测样本与所有训练样本的相似度，常用的有欧氏距离、曼哈顿距离、余弦相似度。

3.筛选 K 近邻：按距离升序排序，选取前 K 个样本作为待预测样本的邻居。

4.决策预测：

分类任务：统计 K 个邻居中各类别频次，频次最高的类别即为预测结果。

回归任务：计算 K 个邻居目标值的均值或加权均值（距离越近权重越高）作为预测结果。

4.关键细节

4.1 距离度量

最常用的是欧氏距离（适合连续特征），也可以用曼哈顿距离、余弦相似度等：


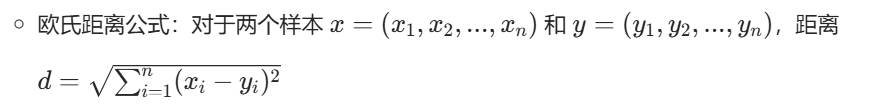
4.2 K 值选择：

K 太小：易受噪声样本影响，模型过拟合；

K 太大：易忽略局部特征，模型欠拟合；

通常取奇数（避免投票平局），如 3、5、7，也可通过交叉验证选最优 K。
4.3数据预处理：

必须做标准化 / 归一化（如你代码中的scale），因为 KNN 依赖距离计算，量纲不同的特征（比如 "身高（厘米）" 和 "体重（公斤）"）会导致距离计算失衡。

二、KNN算法代码

我会分两种方式实现：先手写极简版 KNN 理解核心逻辑，再用 sklearn 实现。
1. 手写极简版 KNN（理解原理）

不调用 sklearn 的 KNN，仅用 numpy 和 collections 手写一个 KNN 分类器，并在鸢尾花数据集上达到 100 % 准确率"的完整流程。帮助完整理解KNN过程。

import numpy as np
from collections import Counter

# 手动实现KNN分类
class SimpleKNN:
    def __init__(self, k=3):
        self.k = k  # 定义近邻数，初始化时指定"看几个邻居"------k 值。
    
    # 训练阶段：KNN是懒惰学习，仅存储训练数据，KNN 是"懒惰学习"：训练阶段什么都不学，只是把训练数据存起来备用。
    def fit(self, X_train, y_train):
        self.X_train = np.array(X_train)
        self.y_train = np.array(y_train)
    
    # 预测单个样本，对单个测试样本 x：计算它与所有训练样本的欧氏距离。排序后选前 k 个最近邻居。看这 k 个邻居都属于哪一类，用 Counter 做多数表决。
    def _predict(self, x):
        # 1. 计算当前样本与所有训练样本的欧氏距离
        distances = np.sqrt(np.sum((self.X_train - x)**2, axis=1))
        # 2. 找到距离最小的k个样本的索引
        k_indices = np.argsort(distances)[:self.k]
        # 3. 取出这k个样本的标签并投票
        k_labels = self.y_train[k_indices]
        # 4. 返回票数最多的标签
        return Counter(k_labels).most_common(1)[0][0]
    
    # 批量预测，对一批测试样本循环调用 _predict，返回预测结果列表。
    def predict(self, X_test):
        return [self._predict(x) for x in X_test]

# 测试手写KNN
if __name__ == "__main__":
    from sklearn.datasets import load_iris
    from sklearn.model_selection import train_test_split
    from sklearn.preprocessing import scale
    from sklearn.metrics import accuracy_score

    # 加载数据+预处理，加载鸢尾花 150 条数据，拆成 80 % 训练、20 % 测试。
    iris = load_iris()
    X = scale(iris.data)
    y = iris.target
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

    # 初始化并训练手写KNN
    knn = SimpleKNN(k=3)
    knn.fit(X_train, y_train)
    y_pred = knn.predict(X_test)

    # 评估准确率，把预测结果与真实标签对比，得到准确率。这里输出 1.00 表示 30 个测试样本全部分类正确（鸢尾花数据本身较简单，k=3 且特征标准化后容易满分）。
    print(f"手写KNN准确率：{accuracy_score(y_test, y_pred):.2f}")  # 输出1.00

2.利用用 sklearn 官方工具做一套完整的 KNN 建模流程

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler  # 替代scale，更灵活
from sklearn.metrics import classification_report

# 1. 加载数据，还是 150 朵鸢尾花，4 个特征 + 1 个标签（0/1/2）。
iris = load_iris()
X, y = iris.data, iris.target

# 2. 数据预处理：标准化（推荐用StandardScaler，可复用），
#StandardScaler 先 fit 计算均值/方差，再 transform 做 Z-score 标准化。
#好处：后续若拿到新样本，只需 scaler.transform(new_X) 即可，保持换算规则一致。

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 3. 划分数据集，stratify=y 保证训练集、测试集里三类花比例与原始数据相同（每类 50 条 → 训练 40/测试 10）。避免某类花在测试集里缺失或过少，导致评估失真。
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=42, stratify=y  # stratify保证标签分布均匀
)

# 4. 选择最优K值（交叉验证），
#在 训练集 上做 5 折交叉验证：把训练集再切成 5 份，轮流用 4 份训练、1 份验证，求平均准确率。
#遍历 k=1,3,5...13，找出 交叉验证平均准确率最高 的 k。
best_k = 3
best_score = 0
for k in range(1, 15, 2):  # 测试1、3、5...13
    knn_temp = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn_temp, X_train, y_train, cv=5)  # 5折交叉验证
    mean_score = scores.mean()
    if mean_score > best_score:
        best_score = mean_score
        best_k = k
print(f"最优K值：{best_k}，对应交叉验证得分：{best_score:.2f}")

# 5. 训练最优K值的模型，用刚才选出的最佳 k，在整个训练集上重新 fit 一次，得到最终模型。
knn = KNeighborsClassifier(n_neighbors=best_k)
knn.fit(X_train, y_train)

# 6. 预测与评估，每类的 precision（查准率）、recall（查全率）、f1-score
y_pred = knn.predict(X_test)
print("\n分类报告：")
print(classification_report(y_test, y_pred))

三、KNN 算法的应用场景

KNN 的优点是简单、无需训练（懒惰学习）、对异常值不敏感（只要 K 合适），缺点是预测时速度慢（需计算所有距离）、内存占用大，因此适合以下场景：
1. 经典应用场景
1.1分类任务：

鸢尾花 / 葡萄酒等小数据集分类（入门场景）；

客户流失预测（根据客户特征判断是否会流失）；

疾病诊断（根据患者的生理指标判断是否患病）；

图像分类（简单图像，如手写数字识别 MNIST）。
1.2回归任务：

房价预测（根据房屋面积、地段等特征预测价格）；

销量预测（根据历史数据预测商品销量）。
2. 适用条件

数据量中小规模（百万级以上数据不适合，可改用 KD 树 / 球树优化，但仍不如树模型）；

特征维度不高（高维数据易出现 "维度灾难"，距离计算失效）；

数据分布相对均匀（样本密度差异大时效果差）。
3. 不适用场景

超大规模数据（如亿级样本）；

高维稀疏数据（如文本词向量、推荐系统的用户行为数据）；

实时性要求极高的场景（如自动驾驶的实时决策）。

总结

核心原理：KNN 是监督学习算法，通过计算待预测样本与训练样本的距离，选取最近的 K 个样本投票分类 / 取平均回归，核心是距离度量和K 值选择；

实现要点：必须做标准化预处理，手写版可理解逻辑，sklearn 版适合实战，还可通过交叉验证选最优 K；

应用场景：适合中小规模、低维度、分布均匀的分类 / 回归任务，不适合超大规模或高维数据场景。