想象一下,你正站在一个圆形广场的中心,周围均匀排列着12根高度不同的灯柱,这就是径向条形图带给我们的视觉体验。
在数据可视化领域,我们常常满足于传统的直角坐标系条形图,但当数据具有周期性或比较性时,径向条形图 和圆形条形图为我们打开了新的可能性。
1. 设计原理
这两种图表把传统的笛卡尔坐标系 换成极坐标系:角度表示类别,半径或角度长度表示数值。
1.1. 径向条形图
径向条形图本质上是将传统条形图的直角坐标系转换为极坐标系。
在极坐标系中,每个数据点不再由(x, y)定位,而是由**(角度, 半径)**确定,条形的高度(或长度)由半径值表示,而条形的排列则沿着圆周方向。
设计灵感:如同钟表的指针或雷达的扫描线,径向条形图借鉴了自然界和人工制品中常见的圆形布局,利用了人类对角度和对称性的天然感知能力。
1.2. 圆形条形图
圆形条形图是径向条形图的一种特殊形式,它固定了起点和终点,使所有条形都在同一圆周上开始,只在半径方向上延伸。
这种设计解决了完全径向布局可能导致的数据比较困难问题,因为所有条形的基准线是一致的。
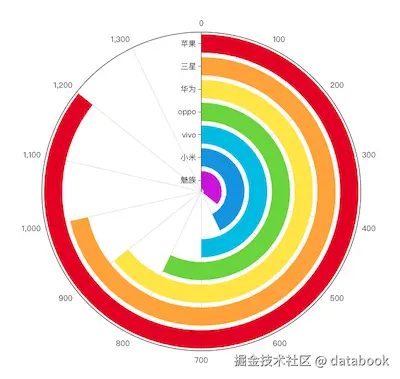
设计比喻:想象一组跳高运动员,他们都从同一高度起跳,只是跳跃的高度不同------圆形条形图就是这样公平的"竞技场"。
2. 应用示例
下面通过示例来演示这两种图在实际场景中的应用。
2.1. 径向条形图
python
# --- 1. 构造测试数据 ---
# 假设我们想比较一年中每个月的平均降水量
月份 = [
"一月",
"二月",
"三月",
"四月",
"五月",
"六月",
"七月",
"八月",
"九月",
"十月",
"十一月",
"十二月",
]
# 生成模拟的降水量数据 (单位: mm)
np.random.seed(42) # 为了结果可复现
降水量 = np.random.uniform(30, 150, size=len(月份)) # 随机生成30-150mm的数据
# --- 2. 创建图形 ---
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 7), facecolor="white")
# --- 2.1 绘制传统条形图 ---
# ... 省略 ...
# --- 2.2 绘制径向条形图 ---
# 计算每个条形的角度位置
# ... 省略 ...
# 使用极坐标子图
ax2 = plt.subplot(122, projection="polar")
# 关键:设置 'bottom' 参数为 inner_radius,这样条形就从 inner_radius 开始画,长度为 radii
bars = ax2.bar(
theta,
radii,
width=0.4,
bottom=inner_radius,
color="lightcoral",
edgecolor="darkred",
alpha=0.7,
)
# 添加数值标签 (在条形内部,靠近外侧)
for angle, radius, month in zip(theta, radii, 月份):
ax2.text(
angle,
inner_radius + radius / 2,
f"{radius:.1f}",
ha="center",
va="center",
fontsize=8,
color="black",
)
# 添加月份标记 (在条形外部)
# ... 省略 ...
# --- 3. 显示图形 ---
plt.tight_layout()
plt.show()这段代码首先生成了模拟的月度降水量数据,然后在同一个图形窗口中创建了两个子图。
左侧是使用 plt.bar 创建的传统条形图,右侧是使用 plt.subplot(..., projection='polar') 和 ax.bar 创建的径向条形图。
径向条形图利用了极坐标系,将类别(月份)分布在圆周上,将数值(降水量)映射到径向长度上。

径向条形图是一种在极坐标系上绘制的图表,可以提供比传统条形图更具视觉吸引力的替代方案。它通过弧长来表示数值,并且可以有效地利用空间,尤其是在处理类别较多或需要强调周期性模式(例如按月份或季度分组的数据)时。
2.2. 圆形条形图
python
from matplotlib import cm
from math import log10
labels = list("ABCDEFG")
data = [21, 57, 88, 14, 76, 91, 26]
# ... 省略 ...
#create colors along a chosen colormap
colors = [cm.terrain(i / n) for i in range(n)]
#create figure, axis
fig, ax = plt.subplots()
#create rings of donut chart
for i in range(n):
current_outer_radius = r - i * w
innerring, _ = ax.pie([m - data[i], data[i]],
radius = current_outer_radius,
startangle = 90,
colors = ["white", colors[i]])
# 添加标签
# ... 省略 ...
plt.show()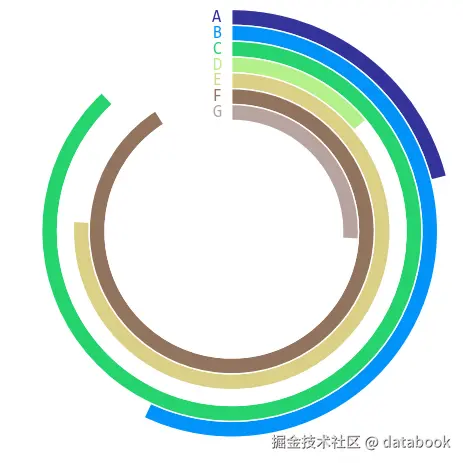
圆形条形图 从同一基准线开始,避免了径向条形图中不同角度起始点不同的问题,更加便于比较。
3. 总结
径向条形图 和圆形条形图代表了数据可视化从纯功能向功能美学平衡的演进。
它们不是要完全取代传统条形图,而是为我们提供了更多视觉叙事的工具。
就像一位熟练的厨师拥有多种刀具一样,优秀的数据分析师也应该掌握多种可视化技术,根据数据特性和沟通目标选择最合适的"刀具"。
当你的数据讲述着周期性的故事,或需要在有限空间内进行多维度比较时,不妨尝试这些圆形可视化方法。它们不仅能更有效地传达信息,还能为你的报告或仪表板增添独特的视觉魅力。
最好的可视化不是最复杂的,而是最能清晰传达数据故事的。
径向 和圆形条形图正是这样一种工具:在传统与现代之间,在功能与美学之间,找到了优雅的平衡点。