TL;DR
- 场景：需要用无监督学习把样本按相似性自动分组，用于客户分群、图像压缩、异常点发现等。
- 结论：K-Means 的核心是"质心迭代 + 最小化簇内平方和(Inertia)"，效果高度依赖特征缩放、K 值与初始化。
- 产出：一套可落地的 K-Means 认知框架（流程/指标/选K/限制）+ 常见报错与修复速查卡。
基本概念
决策树、线性回归和逻辑回归是机器学习中最常用的监督学习算法。它们虽然功能各异（决策树擅长处理非线性关系，线性回归用于连续值预测，逻辑回归解决分类问题），但都属于有监督学习的范畴。这类算法的共同特点是：在模型训练过程中，既需要输入特征矩阵X（包含样本的各个特征），也需要对应的真实标签Y（即目标变量）。训练时，算法会不断调整参数，使预测结果尽可能接近真实标签。
与监督学习相对应的是无监督学习，这类算法在训练时只需要特征矩阵X，不需要标签信息。无监督学习的主要任务是发现数据中隐藏的模式或结构，主要包括两大类算法：
- 聚类算法：用于数据分组
- 降维算法：用于特征压缩
聚类算法被称为"无监督分类"，其核心目标是将数据划分成有意义的组别（称为簇）。这种划分可以基于：
- 业务需求（如客户细分）
- 建模需求（如数据预处理）
- 数据探索（发现自然分布结构）
实际应用场景非常广泛：
-
商业分析案例：
- 客户细分：当企业拥有大量客户数据（包括当前客户和潜在客户）时，可以使用聚类算法将客户划分为不同群体。每个群体具有相似的特征，便于制定针对性的营销策略。
- RFM模型结合：经典的客户价值分析模型RFM（最近一次消费Recency、消费频率Frequency、消费金额Monetary）常与聚类分析配合使用。通过聚类，可以自动识别出高价值客户、潜在流失客户等不同群体。
-
数据处理案例：
- 降维与矢量量化：聚类可用于将高维特征压缩到低维空间，这在处理图像、音频、视频等非结构化数据时特别有用。例如：
- 图像处理：可以将数百万种颜色聚类为256个代表性颜色，大幅减少数据量
- 语音识别：将连续的语音信号聚类为离散的音素单元
- 视频压缩：通过聚类减少关键帧数量，实现高效存储和传输
- 降维与矢量量化：聚类可用于将高维特征压缩到低维空间，这在处理图像、音频、视频等非结构化数据时特别有用。例如：
-
其他应用领域：
- 生物信息学：基因表达数据的聚类分析
- 社交网络：社区发现和用户分群
- 异常检测：识别偏离主要簇的数据点
值得注意的是，聚类结果的质量高度依赖于特征选择、距离度量和聚类算法的选择。常用的聚类算法包括K-means、层次聚类、DBSCAN等，每种算法都有其适用的场景和优缺点。在实际应用中，通常需要尝试多种算法，结合业务知识评估聚类效果。
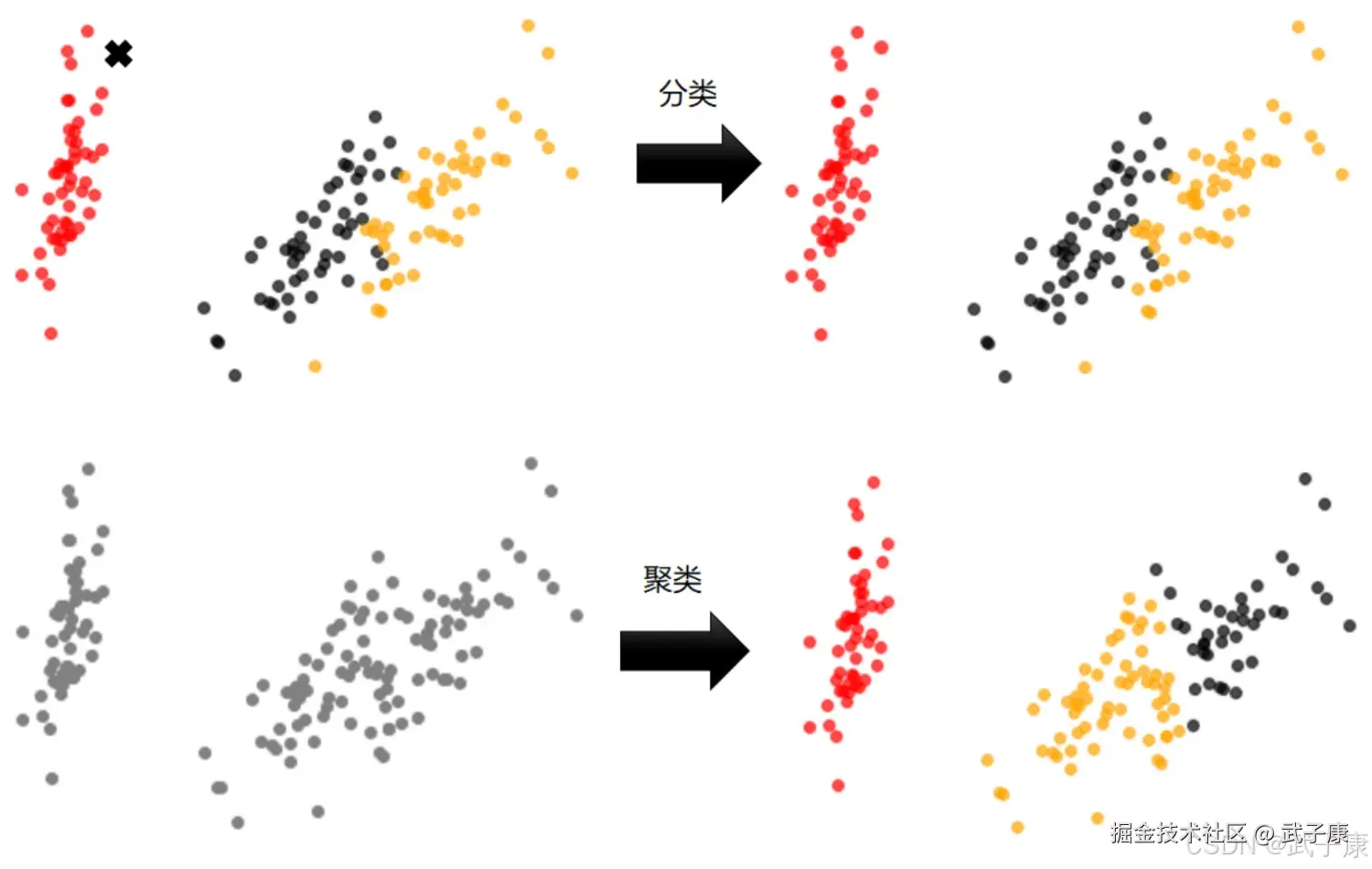对比他们的特征 
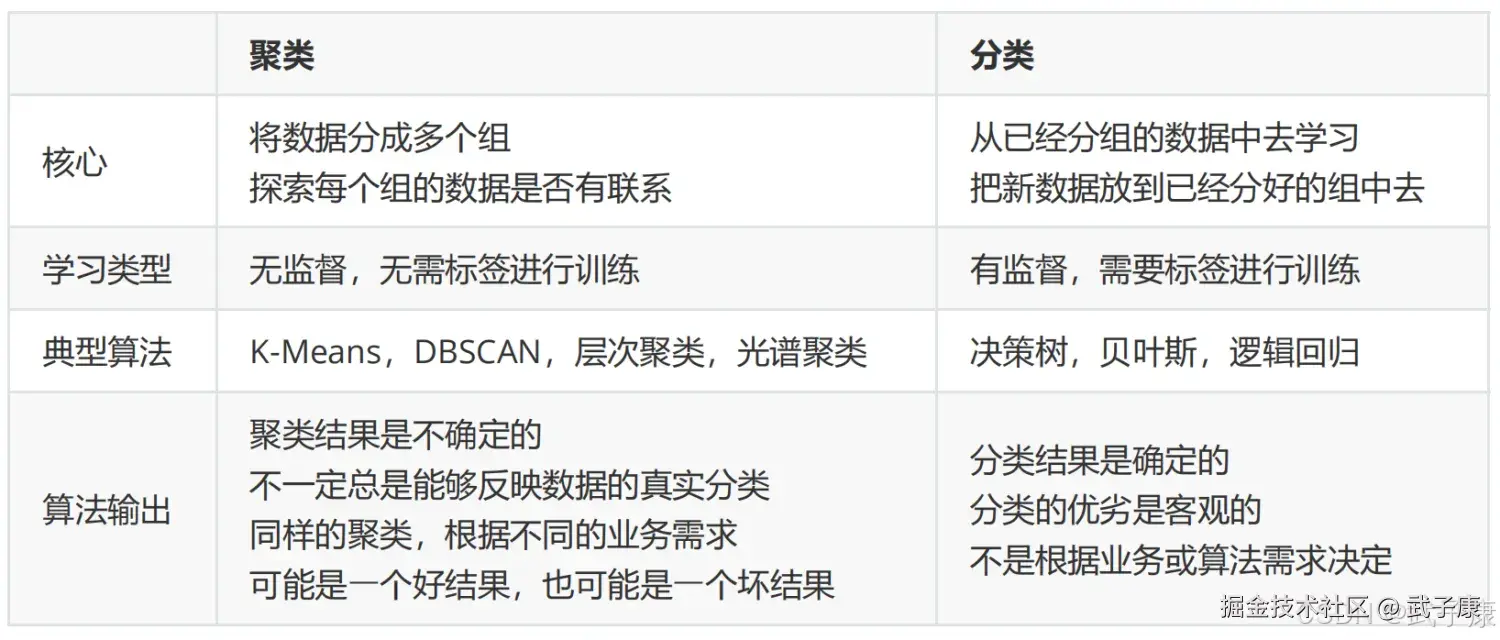聚类算法是无监督类机器学习算法中最常用的一类，其目的是将数据划分成有意义或有用的组（也被称为簇）。这种划分可以基于我们的业务需求或建模需求来完成，也可以单纯的帮助我们探索数据的自然结构和分布。如果目标是划分成有意义的组，则簇应该捕获数据的自然结构。然而，在某种意义下，聚类分析知识解决其他问题（如数据汇总）的起点。无论是皆在理解还是应用，聚类分析都在广泛的领域扮演着重要角色。这些领域包括：心理学和其他社会科学、生物学、统计学、模式识别、信息检索、机器学习、数据挖掘。 聚类分析在许多实际问题上都有应用，下面是一些具体的例子，按聚类目的是为了理解数据自然结构还用于数据处理来组织。
K-Means
基本原理
关键概念：簇和质心
K-Means是一种经典的无监督学习聚类算法，主要用于将一组数据划分为K个簇（Clusters）。这里的K是用户预先定义的聚类数量，需要根据具体问题和数据特点来确定。该算法的核心目标是通过迭代优化，使得同一簇内的数据点之间的距离尽可能接近（高内聚性），而不同簇的数据点之间的距离尽可能远（高区分度）。
KMeans算法的工作流程如下：
- 随机初始化K个质心（centroids）作为初始簇中心
- 计算每个数据点到各质心的距离（通常使用欧氏距离）
- 将每个数据点分配到距离最近的质心所在的簇
- 重新计算每个簇的质心（取簇内所有点的均值）
- 重复步骤2-4直到质心位置不再显著变化或达到最大迭代次数
在实际应用中，KMeans算法将N个样本的特征矩阵X划分为K个互不相交的簇。例如：
- 在客户细分中，每个簇可能代表具有相似消费习惯的客户群体
- 在图像压缩中，每个簇可能代表颜色相近的像素集合
- 在文档分类中，每个簇可能代表主题相似的文档集合
簇质心具有以下重要特性：
- 在二维空间中，质心的坐标(x,y)就是该簇所有点横纵坐标的算术平均值
- 在高维空间中，质心是该簇所有点在每个维度上的均值向量
- 质心不一定是实际存在的数据点，而是计算得出的虚拟中心点
- 随着算法迭代，质心位置会不断调整优化
K值的确定方法：
- 肘部法则（Elbow Method）：通过观察不同K值下误差平方和（SSE）的变化曲线，选择拐点处的K值
- 轮廓系数（Silhouette Coefficient）：衡量聚类效果的指标，取值在-1,1之间，越大表示聚类效果越好
- 基于业务需求：如已知实际类别数或特定业务要求
应用场景示例：
- 市场细分：将消费者分为5个群体（K=5）进行精准营销
- 图像分割：将像素颜色聚类为16种代表色（K=16）实现压缩
- 异常检测：通过聚类找出远离主要簇的离群点
注意事项：
- KMeans对初始质心选择敏感，可能陷入局部最优
- 适用于球形分布数据，对非凸形状簇效果不佳
- 需要数据标准化处理，避免量纲影响距离计算
- 对噪声和离群点较为敏感
工作过程
K-Means 的执行步骤如下：
- 初始化簇中心（质心）：随机选择K个数据点作为初始簇中心，称为质心（Centroid）。
- 分配数据点到簇：对于每一个数据点，计算它到每个质心的欧式距离，并将该数据点分配到距离最近的簇。这样就可以得到K个初始簇。
- 更新质心：对于每一个簇，计算该簇内所有数据点的平均位置，将该平均位置作为新的质心。
- 迭代更新：重复步骤2和步骤3，直到质心位置不再发生明显变化（即达到收敛）或达到最大迭代次数。
具体过程
具体过程可总结如下：
- 创建 K 个点作为初始质心（通常随机选择）
- 当任意一个点的簇分配结果发生改变时：计算质心与数据点之间的距离、将数据点分配到离其最近的簇
- 对每个簇，计算簇中所有点的均值并将均值作为新的质心
- 直到簇不再发生变化或者达到最大的迭代次数
那么什么情况下，我们的质心位置不再发生变化呢？ 当我们找到一个质心，在每次迭代中被分配到这个质心上的样本都是一致的，即每次新生成的簇是一致的，所有的样本点都不会再从一个簇转移到另一个簇，质心就不会变化了。 这个过程可以由下图来显示，我们规定，将数据分为 4（K=4），其中白色 X 代表质心位置： 
在数据的多次迭代下（iteration），就会： 
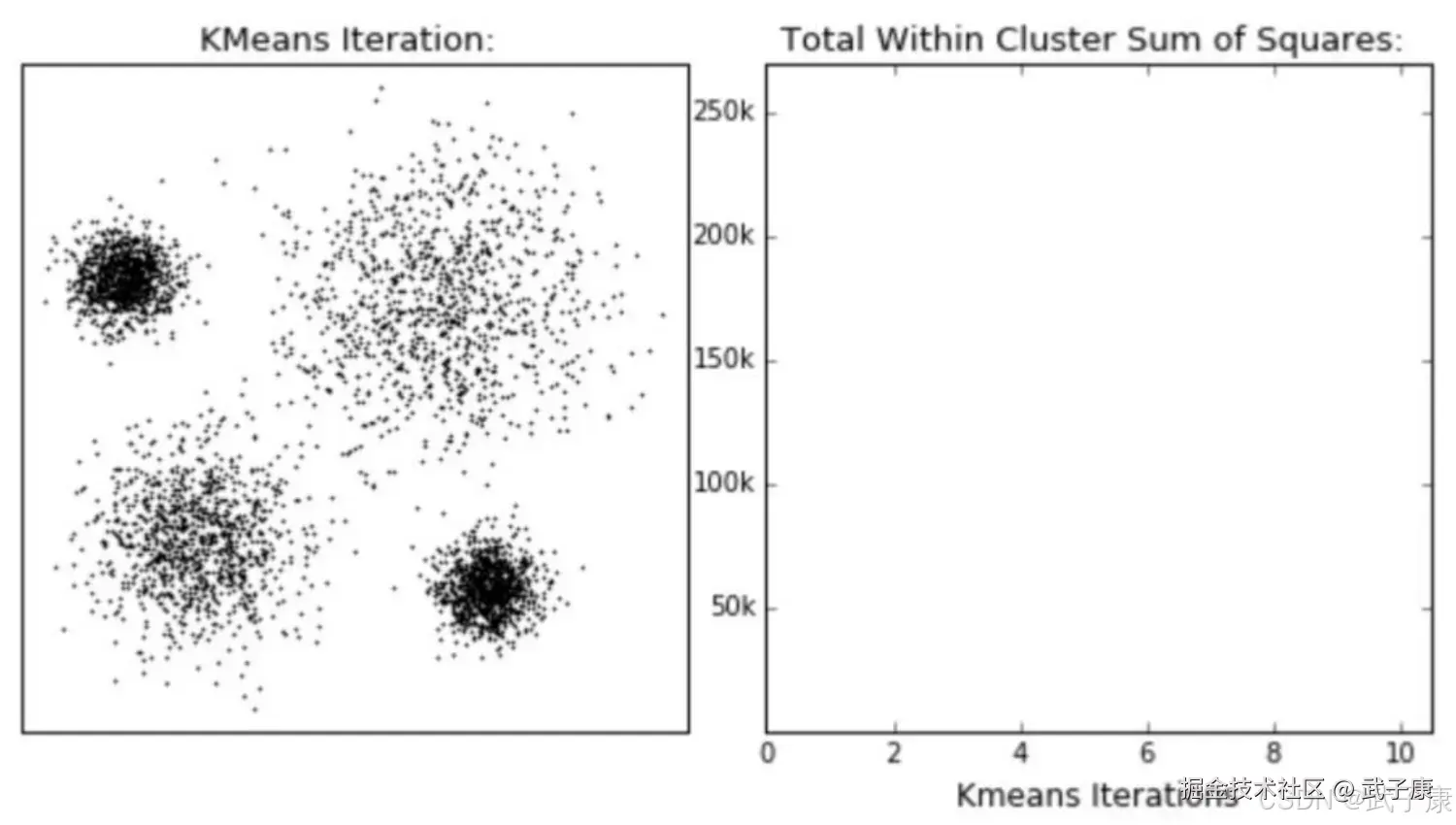第六次迭代之后，基本上质心的位置就不会再改变了，生成的簇也变得稳定，此时我们的聚类就完成了，我们可以明显看出，K-Means 按照数据的分布，将数据聚集成了我们规定的 4 类，接下来我们就可以按照我们的业务求或者算法需求，对四类数据进行不同的处理。
簇内误差平方和
聚类算法出的类有什么含义呢？这些类有什么样的性质？我们认为，被分在同一个簇中的数据是有相似的，而不同的簇中的数据是不同的，当聚类完毕之后，我们就要分别去研究每个簇中的样本都有什么样的性质，从而根据业务需求定制不同的商业或者科技策略。 聚类算法的目的就是追求"簇内差异小，簇外差异大"。而这个差异，由样本到其所在簇的质心的距离来衡量。 对于一个簇来说，所有样本点质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差距离来衡量。 对于一个簇来说，所有样本点到执行距离之和越小，我们就认为这个簇中的样本越来越相似，簇内差异就越小，而距离的衡量方法由多种。
假设：
- x 表示簇中的一个样本点
- u 表示该簇中的质心
- n 表示每个样本点中的特征数目
- i 表示组成点 x 的每个特征编号
则该样本到质心距离可以由以下距离来衡量：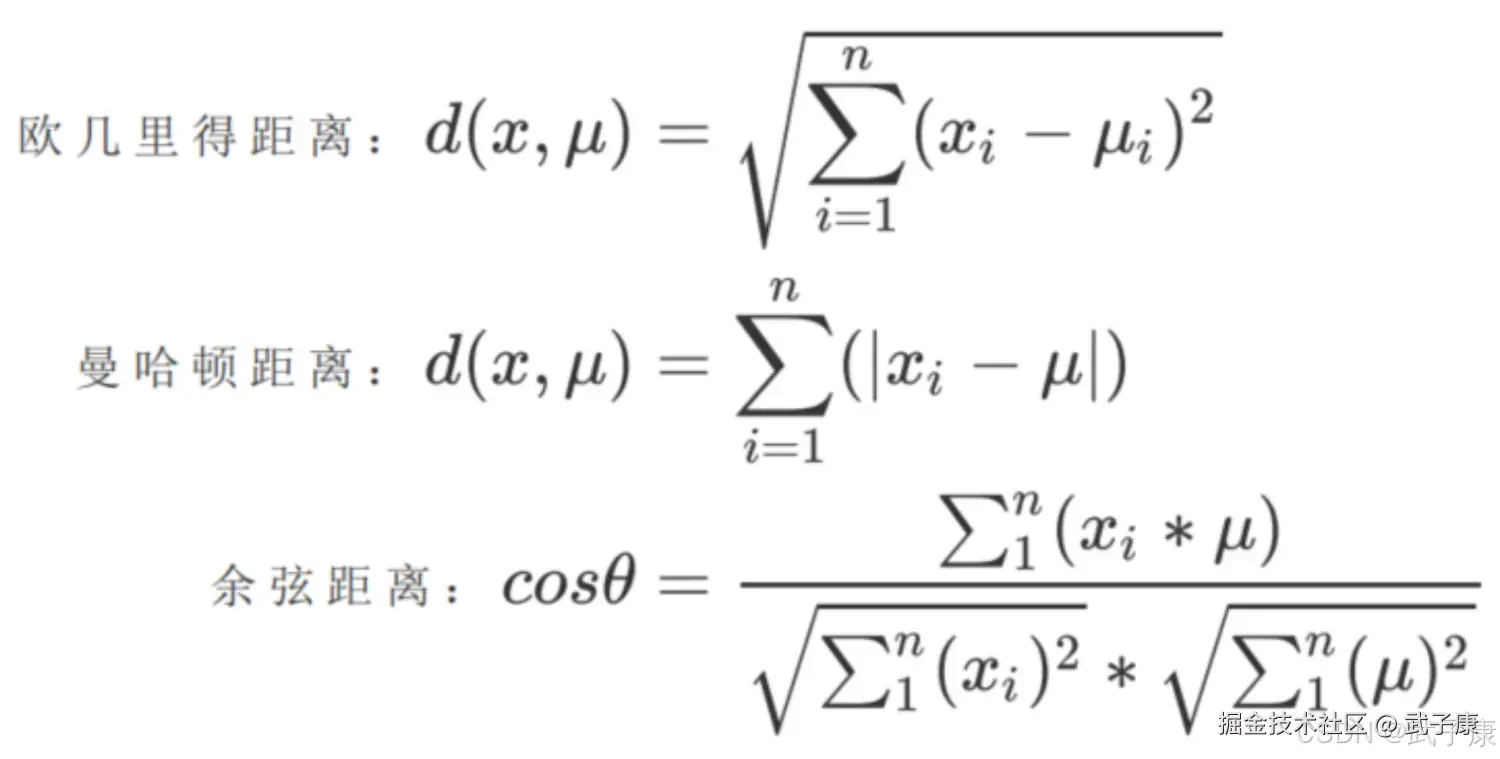 
如果我们采用欧几里得距离，则一个簇中所有样本点的质心距离的平方和为： 
- 其中，m 为一个簇中样本的个数
- j 是每个样本的编号
这个公式被称为簇内平方和（cluster sum of square），又叫做 Inertia。 而将一个数据集中的所有簇的簇内平方和相加，就得到了整体的平方和（Total Cluster Sum Of Square），又叫做 Total Inertia。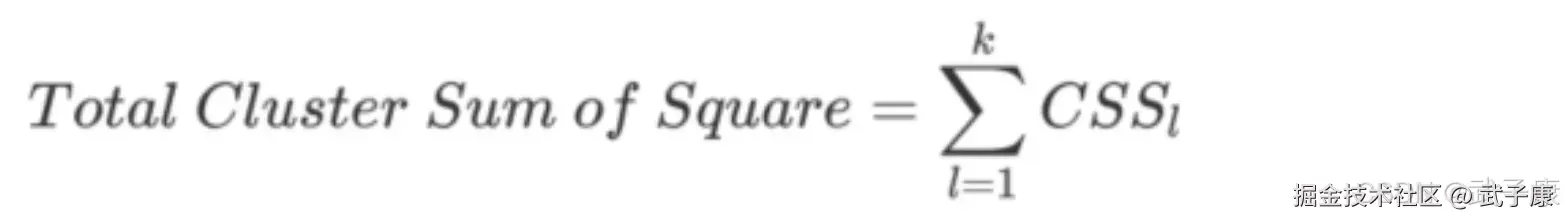 
Total Intertia 越小，代表着每个簇内样本越相似，聚类的效果就越好。 因此 KMeans 追求的是，求解能够让 Inertia 最小化的质心。
实际上，在质心不断变化不断迭代的过程中，总体平方和是越来越小的，当整体平方和最小的时候，质心就不再发生变化了。 大家可以发现，我们的 Intertia 是基于欧几里得距离的计算公式得来的。实际上，我们也可以使用其他距离，每个距离都有自己对应的 Inertia。在过去的经验中，我们总结出距离所对应的质心选择方法和 Inertia，在 KMeans 中，只要使用了正确的质心和距离组合，无论使用什么样的距离，都可以达到不错的聚类效果： 
而这些组合，都可以由严格的数学证明来推导，在实际中我们往往都使用欧式距离，因此我们无需去担忧这些距离所搭配的质心选择是如何得来的。
错误速查
| 症状 | 根因定位 | 修复 |
|---|---|---|
n_samples=... should be >= n_clusters=... |
K 大于样本数 | 检查样本行数、n_clusters；降低 K；或合并/补充样本 |
Input contains NaN, infinity |
特征含 NaN/Inf | 统计缺失/无穷值比例；定位列；缺失值填充/删除；Inf 转换；统一数值范围 |
could not convert string to float / dtype=object |
数据中混入字符串/类别文本 | 查看 DataFrame dtypes；做编码（One-Hot/Label）；或只保留数值列 |
| 结果"分群很怪"、质心被少数大数值维度主导 | 未做特征缩放/量纲不一致 | 查看各特征量级、方差；标准化/归一化；必要时做特征选择/加权 |
ConvergenceWarning: Number of distinct clusters... smaller than n_clusters |
重复样本/离散取值导致可分簇数不足 | 统计重复行；看唯一值数量；去重；降低 K；改用更适合离散数据的方法 |
| 聚类不稳定：同一数据多次跑结果差异大 | 初始化敏感、陷入局部最优 | 多次运行对比 inertia/轮廓系数；提高 n_init；固定 random_state；尝试 k-means++ |
| 非凸形状/密度不均数据聚类效果差 | K-Means 假设"近似球形簇" | 可视化降维后分布；观察边界形状；改用 DBSCAN/HDBSCAN/层次聚类；或先做特征工程 |
| 离群点把质心"拉偏"，簇中心不合理 | 对噪声/离群点敏感 | 查看距离质心最远样本；检查异常值；异常值处理（截断/剔除/鲁棒缩放）；或换算法 |
| 训练慢/内存飙升 | 数据量大、维度高、重复迭代 | 观察样本量N、维度D、迭代次数；降维（PCA）；MiniBatchKMeans；采样/分批训练 |
| SSE/Inertia 下降但业务指标变差 | Inertia 只优化几何距离，不等于业务目标 | 对比业务 KPI（转化、复购、留存）；用业务指标选K/特征；对簇做可解释性校验与回归评估 |
其他系列
🚀 AI篇持续更新中（长期更新）
AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架 私有部署 测试上手 架构研究 ，持续打造实用AI工具指南！ AI研究-132 Java 生态前沿 2025：Spring、Quarkus、GraalVM、CRaC 与云原生落地
💻 Java篇持续更新中（长期更新）
Java-218 RocketMQ Java API 实战：同步/异步 Producer 与 Pull/Push Consumer MyBatis 已完结，Spring 已完结，Nginx已完结，Tomcat已完结，分布式服务已完结，Dubbo已完结，MySQL已完结，MongoDB已完结，Neo4j已完结，FastDFS 已完结，OSS已完结，GuavaCache已完结，EVCache已完结，RabbitMQ已完结，RocketMQ正在更新... 深入浅出助你打牢基础！
📊 大数据板块已完成多项干货更新（300篇）：
包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！ 大数据-278 Spark MLib - 基础介绍 机器学习算法 梯度提升树 GBDT案例 详解