码分正交导频设计
码分正交导频允许大于一个antenna 在同一个导频资源上发送导频。这要求不同天线端口的导频序列正交,导频序列资源数大于天线端口数。使用正交导频不可避免的会存在干扰,这个是不可避免的。例如存在两个发送资源,两个天线端口:
y1y2\]=\[111−1\]\[h11h12h21h22\]+\[n1n2\] \\begin{bmatrix} y_1\\\\ y_2 \\end{bmatrix}= \\begin{bmatrix} 1\&1\\\\ 1\&-1 \\end{bmatrix} \\begin{bmatrix} h_{11}\&h_{12}\\\\ h_{21}\&h_{22}\\\\ \\end{bmatrix} + \\begin{bmatrix} n_1\\\\ n_2 \\end{bmatrix} \[y1y2\]=\[111−1\]\[h11h21h12h22\]+\[n1n2
h11h_{11}h11表示导频从天线端口1发送第一个resource的信道响应,h12h_{12}h12表示导频从天线端口1发送的第二个resource的信道响应。h21,h22h_{21},h_{22}h21,h22同理表示第二个天线端口发送的两个resource的信号响应。如果同一个天线端口的两个资源的信道响应相等 即:h11=h12=h1ˉ,h21=h22=h2ˉh_{11}=h_{12}=\bar{h_{1}},h_{21}=h_{22}=\bar{h_{2}}h11=h12=h1ˉ,h21=h22=h2ˉ,且nk=0n_{k}=0nk=0,则我们可以得一个方程组:
y1=h11+h21y2=h12−h22⇓h1ˉ=12(y1+y2)h2ˉ=12(y1−y2) y_{1}=h_{11}+h_{21}\\ y_{2}=h_{12}-h_{22}\\ \Downarrow\\ \bar{h_{1}}=\frac{1}{2}(y_1+y_2)\\ \bar{h_{2}}=\frac{1}{2}(y_{1}-y_{2}) y1=h11+h21y2=h12−h22⇓h1ˉ=21(y1+y2)h2ˉ=21(y1−y2)
如果我们假设了上述前提那么误差是不可避免的工程就是这样无数学的完备解就假设,但是往往假设后效果也挺好。
PDSCH信道正交导频结构设计
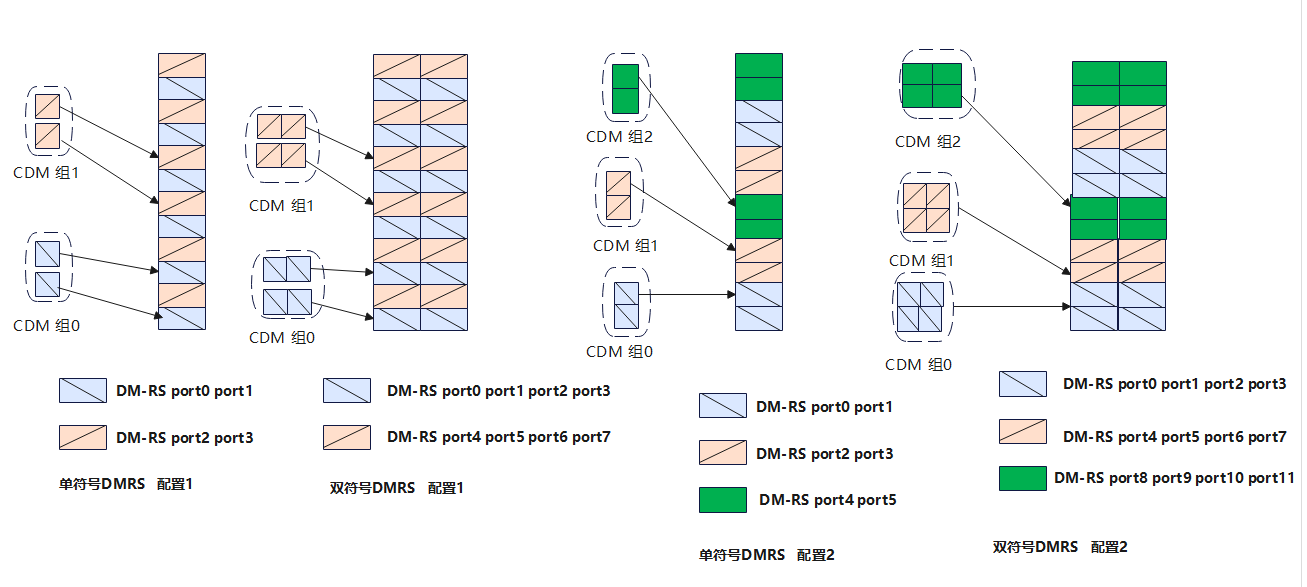
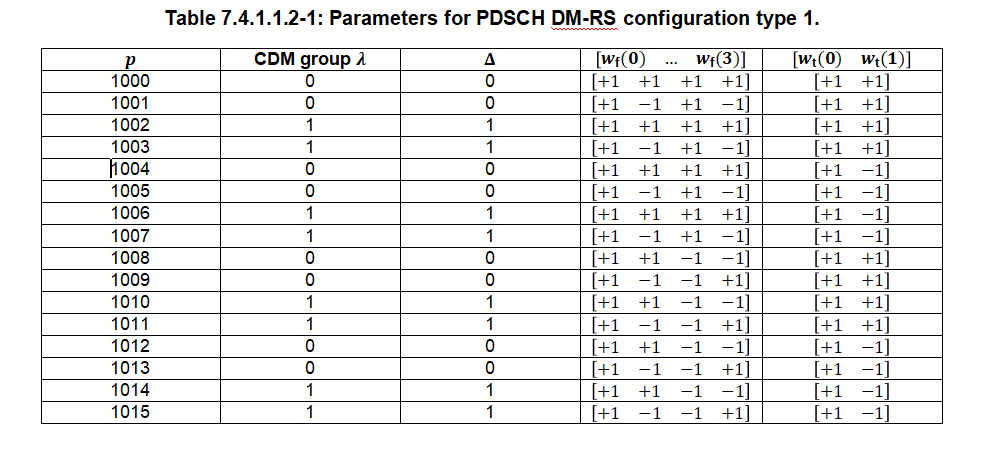
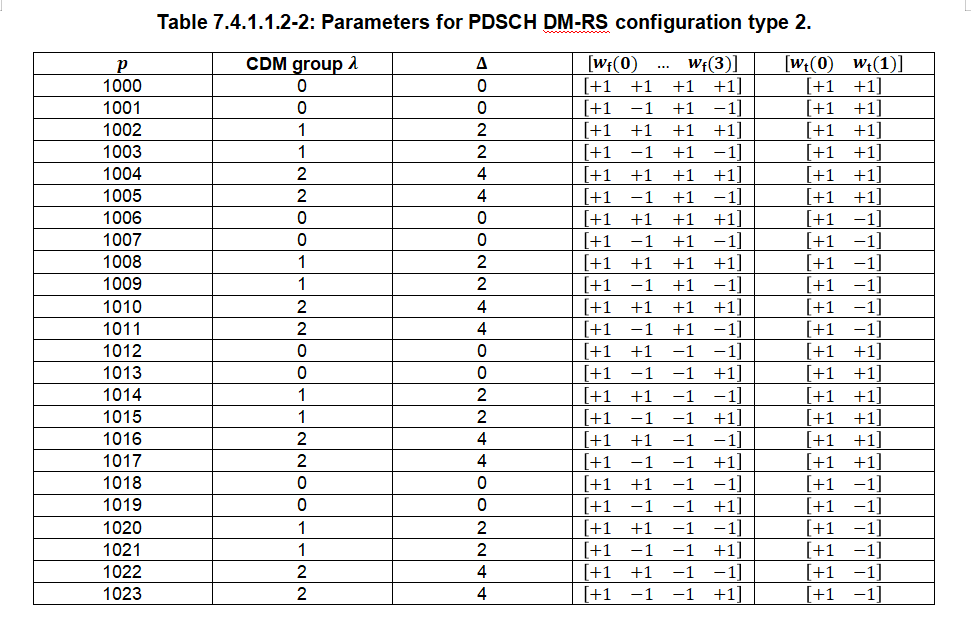
ak,l(p,μ)=βPDSCH⋅wf(k′)⋅wt(l′)⋅r(2n+k′) a_{k,l}^{(p,\mu)} = \beta_{\text{PDSCH}} \cdot w_f(k') \cdot w_t(l') \cdot r(2n + k') ak,l(p,μ)=βPDSCH⋅wf(k′)⋅wt(l′)⋅r(2n+k′)
其中wf(k′),wt(l′)w_f(k^{\prime}),w_{t}(l^{\prime})wf(k′),wt(l′)分别表示频域和时域正交码
CSI 正交导频结构设计
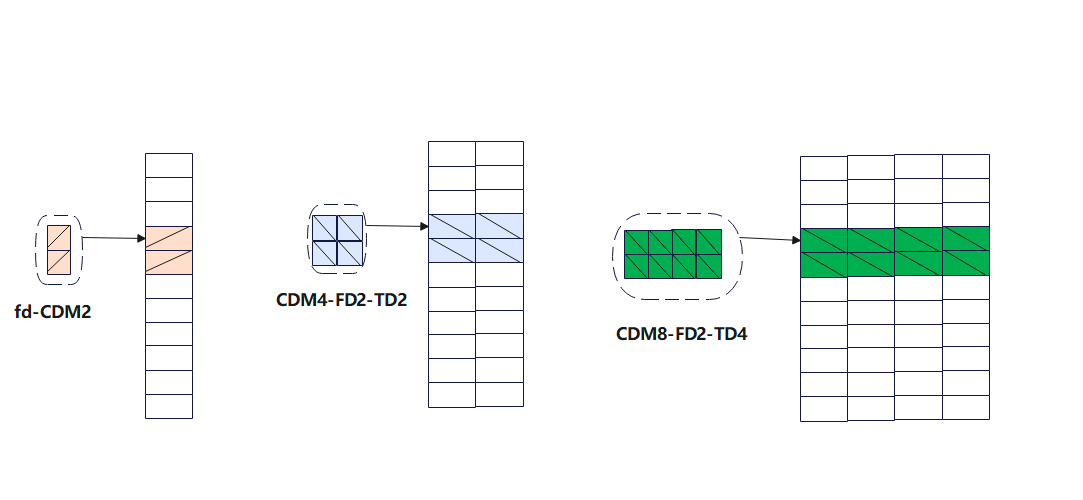
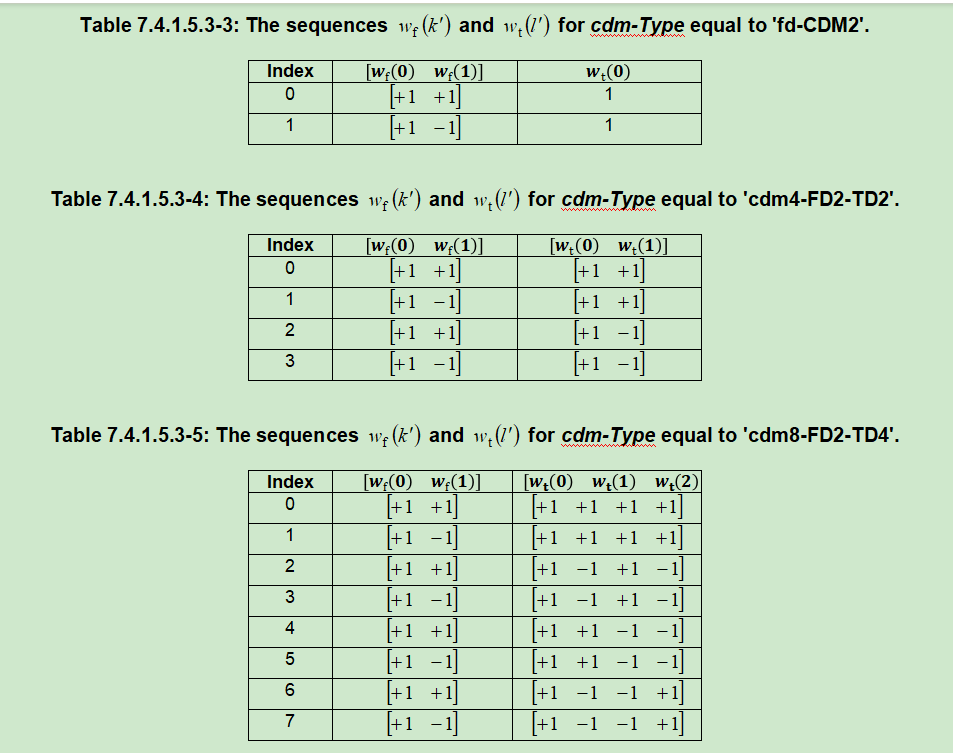
解OCC
我们已fd-CDM2为例进行说明。假设同一个CDM group 内部相同port 在所有资源的信道冲击响应相同Descramble1,Descramble2Descramble1,Descramble2Descramble1,Descramble2分别表示解扰后的信道冲击响应,Despreading1,Despreading2Despreading1,Despreading2Despreading1,Despreading2,每个port的真实信道冲击响应,由导频码可得。
Descramble1=Despreading1+Despreading2Descramble2=Despreading1−Despreading2⇓Despreading1=Descramble1+Descramble22Despreading2=Descramble1−Descramble22 Descramble1=Despreading1+Despreading2\\ Descramble2=Despreading1-Despreading2\\ \Downarrow\\ Despreading1=\frac{Descramble1+Descramble2}{2}\\ Despreading2=\frac{Descramble1-Descramble2}{2}\\ Descramble1=Despreading1+Despreading2Descramble2=Despreading1−Despreading2⇓Despreading1=2Descramble1+Descramble2Despreading2=2Descramble1−Descramble2
得到Despreading1,Despreading2Despreading1,Despreading2Despreading1,Despreading2 就可以进行后续滤波处理,当然有的实现是先进行WIENER 滤波后再解OCC。这个根据算法仿真性能分析自行选择。
同理CDM4-FD2-TD2解OCC方式如下其中h0,h1,h2,h3h_0,h_1,h_2,h_3h0,h1,h2,h3表示每个port的信道冲击响应,H0,H1,H2,H3H_0,H_1,H_2,H_3H0,H1,H2,H3表示每个资源解扰后的信道冲击响应:
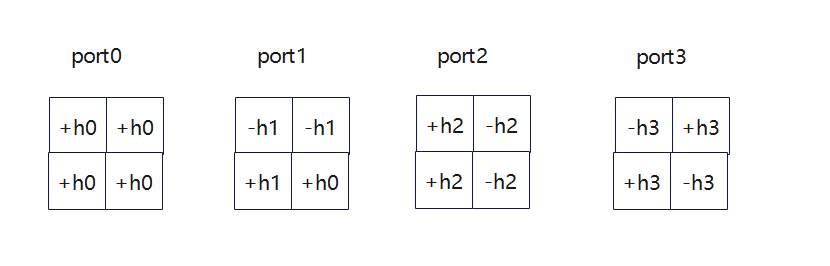
H0=h0+h1+h2+h3H1=h0−h1+h2−h3H2=h0+h1−h2−h3H3=h0−h1−h2+h3⇓h0=H0+H1+H2+H34h1=H0−H1+H2−H34h2=H0+H1−H2−H34h3=H0−H1−H2+H34 H_0=h_0+h_1+h_2+h_3\\ H_1=h_0-h_1+h_2-h_3\\ H_2=h_0+h_1-h_2-h_3\\ H_3=h_0-h_1-h_2+h3\\ \Downarrow\\ h_0=\frac{H_0+H_1+H_2+H_3}{4}\\ h_1=\frac{H_0-H_1+H2-H_3}{4}\\ h_2=\frac{H_0+H_1-H_2-H_3}{4}\\ h_3=\frac{H_0-H_1-H_2+H_3}{4} H0=h0+h1+h2+h3H1=h0−h1+h2−h3H2=h0+h1−h2−h3H3=h0−h1−h2+h3⇓h0=4H0+H1+H2+H3h1=4H0−H1+H2−H3h2=4H0+H1−H2−H3h3=4H0−H1−H2+H3
同理可得CDM8-FD2-TD4:
h0=H0+H1+H2+H3+H4+H5+H6+H78h1=H0−H1+H2−H3+H4−H5+H6−H78h2=H0+H1−H2−H3+H4+H5−H6−H78h3=H0−H1−H2+H3+H4−H5−H6+H78h4=H0+H1+H2+H3−H4−H5−H6−H78h5=H0−H1+H2−H3−H4+H5−H6+H78h6=H0+H1−H2−H3−H4−H5+H6+H78h7=H0−H1−H2+H3−H4+H5+H6−H78 h_0=\frac{H_0+H_1+H_2+H_3+H_4+H_5+H6+H_7}{8}\\ h_1=\frac{H_0-H_1+H2-H_3+H_4-H_5+H_6-H_7}{8}\\ h_2=\frac{H_0+H_1-H_2-H_3+H_4+H_5-H_6-H_7}{8}\\ h_3=\frac{H_0-H_1-H_2+H_3+H_4-H_5-H_6+H_7}{8}\\ h_4=\frac{H_0+H_1+H_2+H_3-H_4-H_5-H_6-H_7}{8}\\ h_5=\frac{H_0-H_1+H_2-H_3-H_4+H_5-H_6+H_7}{8}\\ h_6=\frac{H_0+H_1-H_2-H_3-H_4-H_5+H_6+H_7}{8}\\ h_7=\frac{H_0-H_1-H_2+H_3-H_4+H_5+H_6-H_7}{8} h0=8H0+H1+H2+H3+H4+H5+H6+H7h1=8H0−H1+H2−H3+H4−H5+H6−H7h2=8H0+H1−H2−H3+H4+H5−H6−H7h3=8H0−H1−H2+H3+H4−H5−H6+H7h4=8H0+H1+H2+H3−H4−H5−H6−H7h5=8H0−H1+H2−H3−H4+H5−H6+H7h6=8H0+H1−H2−H3−H4−H5+H6+H7h7=8H0−H1−H2+H3−H4+H5+H6−H7