在cesium中存在多种坐标系,因为cesium作为一个空间地理的渲染引擎,需要处理从地理坐标到3D渲染的转换,理解这些坐标之间的联系,是cesium的基础。也是任何一个地理渲染引擎的基础。
这篇文章带大家理解cesium中的坐标系,顺便对比一下three.js的区别。
1、WGS84
WGS 84是全球定位系统(GPS)的基准坐标系统,广泛应用于全球定位和导航。它采用十进制度表示经度和纬度。(这句话是摘录维基百科的介绍)
简而言之这个坐标系统用的是用经纬度来表示位置
2、经纬高
用经纬度和高程来表示空间位置
- 经度(longitude):范围 [-π, π],单位弧度
- 纬度(latitude):范围 [-π/2, π/2],单位弧度
- 高度(height):相对于椭球面的高度,单位米
在 Cesium 中用 Cartographic 表示,注意角度单位为弧度。
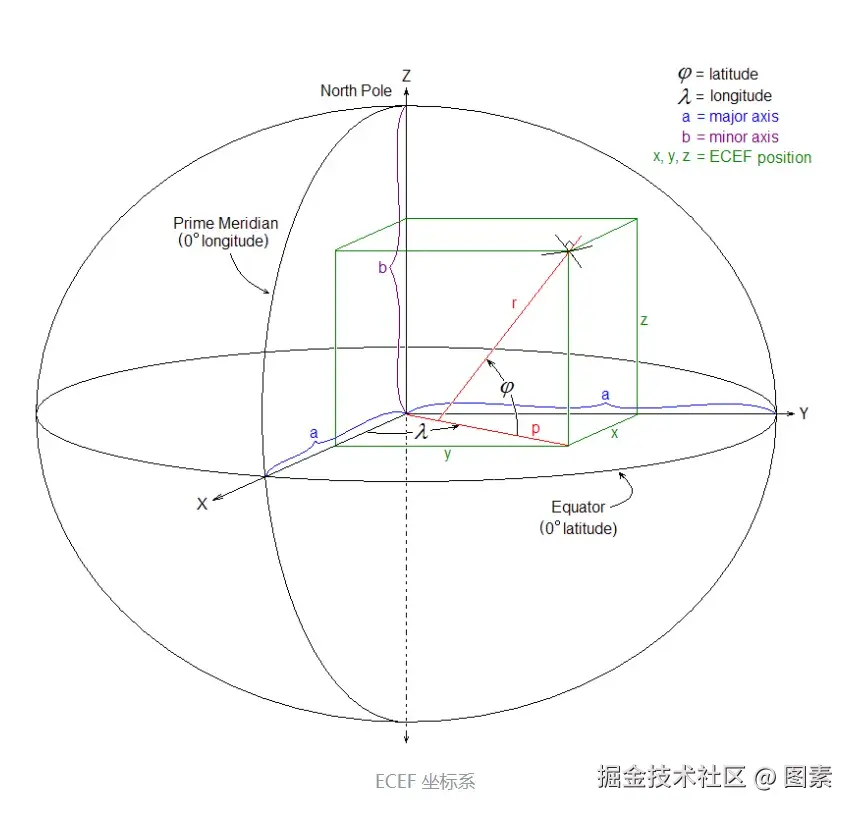
3、ECEF(Earth-Centered, Earth-Fixed)
地心地固坐标系,也称为三维笛卡尔坐标
- 原点:地心
- X 轴:指向本初子午线与赤道交点
- Z 轴:指向北极
- Y 轴:与 X、Z 构成右手系
在 Cesium 中用 Cartesian3 表示,单位为米。这是 Cesium 场景中的世界坐标。

上图为ECEF坐标系
结论:Cesium的世界坐标系就是ECEF坐标系。所有三维物体都是基于这个坐标系进行摆放,三维物体通过 modelMatrix会把局部坐标系转化为世界坐标系
cesium中常用的坐标转换方法
经纬度->笛卡尔
scss
// 经纬度是角度值时候转为笛卡尔
Cesium.Cartesian3.fromDegrees(lonDeg, latDeg, height, ellipsoid?, result?)
// 弧度制时转为笛卡尔
Cesium.Cartesian3.fromRadians(lonRad, latRad, height, ellipsoid?, result?)
// 通过球体转为笛卡尔
ellipsoid.cartographicToCartesian(cartographic, result?)我们来根据源码来看看经纬度是如何计算出笛卡尔坐标的:
ini
/**
* Returns a Cartesian3 position from longitude and latitude values given in radians.
*
* @param {number} longitude The longitude, in radians
* @param {number} latitude The latitude, in radians
* @param {number} [height=0.0] The height, in meters, above the ellipsoid.
* @param {Ellipsoid} [ellipsoid=Ellipsoid.default] The ellipsoid on which the position lies.
* @param {Cartesian3} [result] The object onto which to store the result.
* @returns {Cartesian3} The position
*
* @example
* const position = Cesium.Cartesian3.fromRadians(-2.007, 0.645);
*/
Cartesian3.fromRadians = function (
longitude,
latitude,
height,
ellipsoid,
result,
) {
//>>includeStart('debug', pragmas.debug);
Check.typeOf.number("longitude", longitude);
Check.typeOf.number("latitude", latitude);
//>>includeEnd('debug');
height = height ?? 0.0;
const radiiSquared = !defined(ellipsoid)
? Cartesian3._ellipsoidRadiiSquared
: ellipsoid.radiiSquared;
const cosLatitude = Math.cos(latitude);
// 如上图可以求得 从原点指向目标点的向量 scratchN
scratchN.x = cosLatitude * Math.cos(longitude);
scratchN.y = cosLatitude * Math.sin(longitude);
scratchN.z = Math.sin(latitude);
// 得到球心指向椭球面的向量
scratchN = Cartesian3.normalize(scratchN, scratchN);
// 这个地方cesium 用的计算方法我也没有推导过,数学好的可以自己推导一下
// 最简单的使用解析几何的椭圆公式和向量的交点,可以求出椭圆上的点
// cesium这里的方法计算方式更简洁一点,通过计算缩放因子把向量缩放到椭圆上
Cartesian3.multiplyComponents(radiiSquared, scratchN, scratchK);
const gamma = Math.sqrt(Cartesian3.dot(scratchN, scratchK));
// 得到椭圆上的点坐标
scratchK = Cartesian3.divideByScalar(scratchK, gamma, scratchK);
// 得到长度为height的地心方向向量的向量
scratchN = Cartesian3.multiplyByScalar(scratchN, height, scratchN);
if (!defined(result)) {
result = new Cartesian3();
}
// 最后把椭圆上的点再验证地心法线平移height,得到ecef坐标
return Cartesian3.add(scratchK, scratchN, result);
};笛卡尔->经纬度
scss
Cesium.Cartographic.fromCartesian(cartesian, ellipsoid?, result?)
ellipsoid.cartesianToCartographic(cartesian, result?)源码的计算过程:还挺复杂的,用的牛顿迭代法,数学好的朋友可以自行去推导。
ini
/**
* Creates a new Cartographic instance from a Cartesian position. The values in the
* resulting object will be in radians.
*
* @param {Cartesian3} cartesian The Cartesian position to convert to cartographic representation.
* @param {Ellipsoid} [ellipsoid=Ellipsoid.default] The ellipsoid on which the position lies.
* @param {Cartographic} [result] The object onto which to store the result.
* @returns {Cartographic} The modified result parameter, new Cartographic instance if none was provided, or undefined if the cartesian is at the center of the ellipsoid.
*/
Cartographic.fromCartesian = function (cartesian, ellipsoid, result) {
const oneOverRadii = defined(ellipsoid)
? ellipsoid.oneOverRadii
: Cartographic._ellipsoidOneOverRadii;
const oneOverRadiiSquared = defined(ellipsoid)
? ellipsoid.oneOverRadiiSquared
: Cartographic._ellipsoidOneOverRadiiSquared;
const centerToleranceSquared = defined(ellipsoid)
? ellipsoid._centerToleranceSquared
: Cartographic._ellipsoidCenterToleranceSquared;
//`cartesian is required.` is thrown from scaleToGeodeticSurface
const p = scaleToGeodeticSurface(
cartesian,
oneOverRadii,
oneOverRadiiSquared,
centerToleranceSquared,
cartesianToCartographicP,
);
if (!defined(p)) {
return undefined;
}
let n = Cartesian3.multiplyComponents(
p,
oneOverRadiiSquared,
cartesianToCartographicN,
);
n = Cartesian3.normalize(n, n);
const h = Cartesian3.subtract(cartesian, p, cartesianToCartographicH);
const longitude = Math.atan2(n.y, n.x);
const latitude = Math.asin(n.z);
const height =
CesiumMath.sign(Cartesian3.dot(h, cartesian)) * Cartesian3.magnitude(h);
if (!defined(result)) {
return new Cartographic(longitude, latitude, height);
}
result.longitude = longitude;
result.latitude = latitude;
result.height = height;
return result;
};
/**
* Scales the provided Cartesian position along the geodetic surface normal
* so that it is on the surface of this ellipsoid. If the position is
* at the center of the ellipsoid, this function returns undefined.
*
* @param {Cartesian3} cartesian The Cartesian position to scale.
* @param {Cartesian3} oneOverRadii One over radii of the ellipsoid.
* @param {Cartesian3} oneOverRadiiSquared One over radii squared of the ellipsoid.
* @param {number} centerToleranceSquared Tolerance for closeness to the center.
* @param {Cartesian3} [result] The object onto which to store the result.
* @returns {Cartesian3} The modified result parameter, a new Cartesian3 instance if none was provided, or undefined if the position is at the center.
*
* @function scaleToGeodeticSurface
*
* @private
*/
function scaleToGeodeticSurface(
cartesian,
oneOverRadii,
oneOverRadiiSquared,
centerToleranceSquared,
result,
) {
//>>includeStart('debug', pragmas.debug);
if (!defined(cartesian)) {
throw new DeveloperError("cartesian is required.");
}
if (!defined(oneOverRadii)) {
throw new DeveloperError("oneOverRadii is required.");
}
if (!defined(oneOverRadiiSquared)) {
throw new DeveloperError("oneOverRadiiSquared is required.");
}
if (!defined(centerToleranceSquared)) {
throw new DeveloperError("centerToleranceSquared is required.");
}
//>>includeEnd('debug');
const positionX = cartesian.x;
const positionY = cartesian.y;
const positionZ = cartesian.z;
const oneOverRadiiX = oneOverRadii.x;
const oneOverRadiiY = oneOverRadii.y;
const oneOverRadiiZ = oneOverRadii.z;
const x2 = positionX * positionX * oneOverRadiiX * oneOverRadiiX;
const y2 = positionY * positionY * oneOverRadiiY * oneOverRadiiY;
const z2 = positionZ * positionZ * oneOverRadiiZ * oneOverRadiiZ;
// Compute the squared ellipsoid norm.
const squaredNorm = x2 + y2 + z2;
const ratio = Math.sqrt(1.0 / squaredNorm);
// As an initial approximation, assume that the radial intersection is the projection point.
const intersection = Cartesian3.multiplyByScalar(
cartesian,
ratio,
scaleToGeodeticSurfaceIntersection,
);
// If the position is near the center, the iteration will not converge.
if (squaredNorm < centerToleranceSquared) {
return !isFinite(ratio)
? undefined
: Cartesian3.clone(intersection, result);
}
const oneOverRadiiSquaredX = oneOverRadiiSquared.x;
const oneOverRadiiSquaredY = oneOverRadiiSquared.y;
const oneOverRadiiSquaredZ = oneOverRadiiSquared.z;
// Use the gradient at the intersection point in place of the true unit normal.
// The difference in magnitude will be absorbed in the multiplier.
const gradient = scaleToGeodeticSurfaceGradient;
gradient.x = intersection.x * oneOverRadiiSquaredX * 2.0;
gradient.y = intersection.y * oneOverRadiiSquaredY * 2.0;
gradient.z = intersection.z * oneOverRadiiSquaredZ * 2.0;
// Compute the initial guess at the normal vector multiplier, lambda.
let lambda =
((1.0 - ratio) * Cartesian3.magnitude(cartesian)) /
(0.5 * Cartesian3.magnitude(gradient));
let correction = 0.0;
let func;
let denominator;
let xMultiplier;
let yMultiplier;
let zMultiplier;
let xMultiplier2;
let yMultiplier2;
let zMultiplier2;
let xMultiplier3;
let yMultiplier3;
let zMultiplier3;
do {
lambda -= correction;
xMultiplier = 1.0 / (1.0 + lambda * oneOverRadiiSquaredX);
yMultiplier = 1.0 / (1.0 + lambda * oneOverRadiiSquaredY);
zMultiplier = 1.0 / (1.0 + lambda * oneOverRadiiSquaredZ);
xMultiplier2 = xMultiplier * xMultiplier;
yMultiplier2 = yMultiplier * yMultiplier;
zMultiplier2 = zMultiplier * zMultiplier;
xMultiplier3 = xMultiplier2 * xMultiplier;
yMultiplier3 = yMultiplier2 * yMultiplier;
zMultiplier3 = zMultiplier2 * zMultiplier;
func = x2 * xMultiplier2 + y2 * yMultiplier2 + z2 * zMultiplier2 - 1.0;
// "denominator" here refers to the use of this expression in the velocity and acceleration
// computations in the sections to follow.
denominator =
x2 * xMultiplier3 * oneOverRadiiSquaredX +
y2 * yMultiplier3 * oneOverRadiiSquaredY +
z2 * zMultiplier3 * oneOverRadiiSquaredZ;
const derivative = -2.0 * denominator;
correction = func / derivative;
} while (Math.abs(func) > CesiumMath.EPSILON12);
if (!defined(result)) {
return new Cartesian3(
positionX * xMultiplier,
positionY * yMultiplier,
positionZ * zMultiplier,
);
}
result.x = positionX * xMultiplier;
result.y = positionY * yMultiplier;
result.z = positionZ * zMultiplier;
return result;
}弧度/角度换算
- Cesium.Math.toRadians(deg)
- Cesium.Math.toDegrees(rad)
Three.js 中的世界坐标系
最后我们来对比一下Three.js 中的世界坐标系,看下图,
Three.js 世界坐标中心点可以是任意点,通常放在内容的中心。默认右手坐标系,并且约定+Y向上,相机默认朝 -Z 方向看(所以"前方"常被理解为 -Z)向后(+Z)
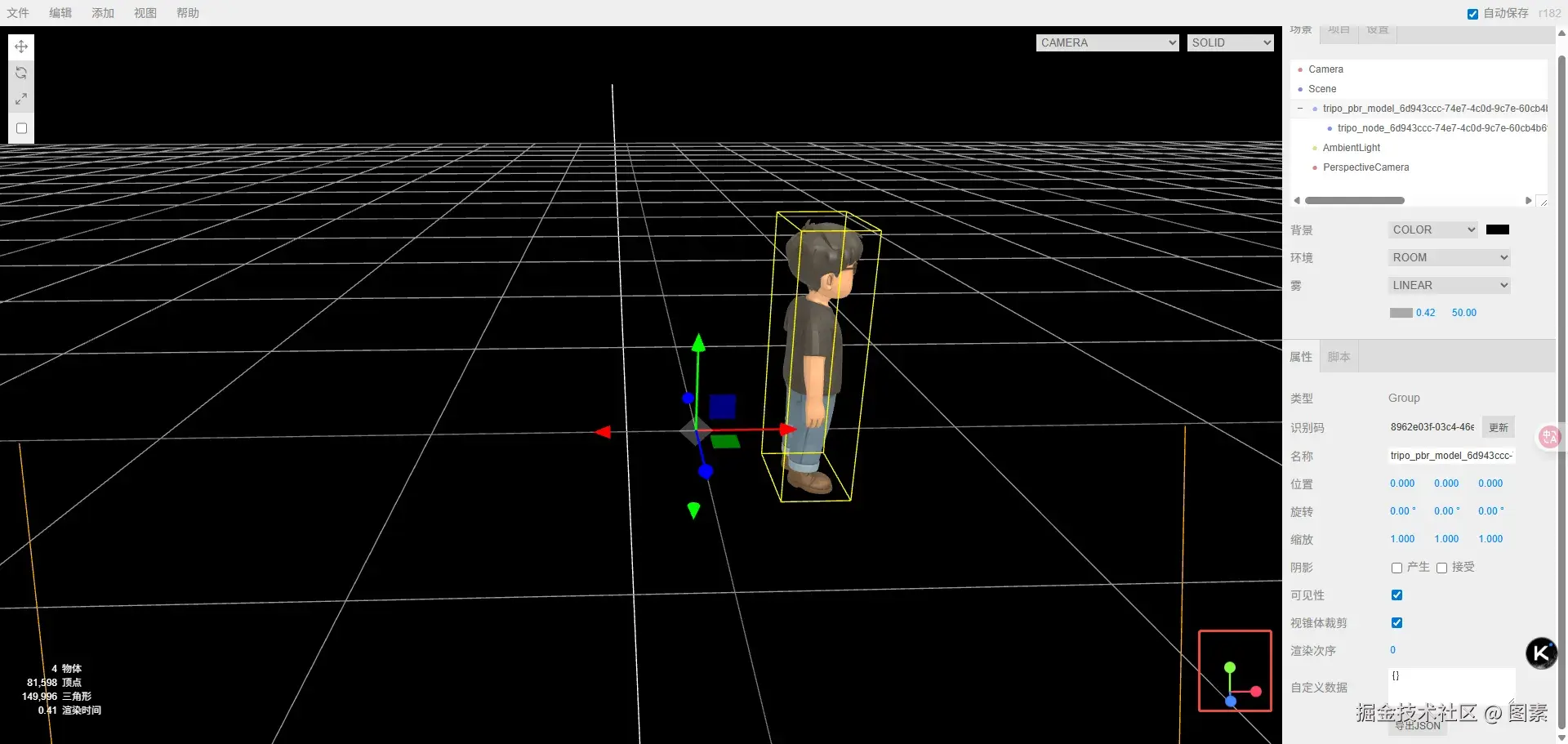
three.js 世界坐标系