一、子集
1、题目

2、分析
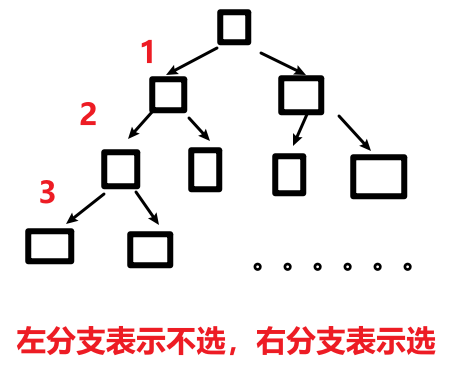
- 类似递归深度遍历,但是需要回溯(回到上一层:路径长度复原、路径值复原)。
- 时间复杂度:类似深度遍历,n层树,遍历时间为结点数2^(n+1) - 1,有2^n种方案即叶子节点个数,每个方案需要复制n次。O(2^(n+1) - 1 + n*2^n) = O( n*2^n)。
- 空间复杂度:递归深度,即树高,O(n)。
3、代码
java
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<Integer> tmp = new ArrayList<>(); // 暂存当前路径值
int pathLen = 0; // 当前路径长度
List<List<Integer>> ret = new ArrayList<>(); // 存结果
subsets(nums, tmp, pathLen, ret);
return ret;
}
public void subsets(int[] nums, List<Integer> tmp, int pathLen, List<List<Integer>> ret) {
// 递归结束条件:遍历到叶子节点,找到一条路径
if (nums.length == pathLen) {
ret.add(new ArrayList<>(tmp)); // 存在复制操作
return;
}
// 遍历左分支:选取第 pathLen+1 层元素
tmp.add(nums[pathLen]);
subsets(nums, tmp, pathLen+1, ret);
// 回溯
tmp.remove(tmp.size()-1);
// 遍历右分支:不选取第 pathLen+1 层元素
subsets(nums, tmp, pathLen+1, ret);
}
}二、全排列
1、题目

2、分析
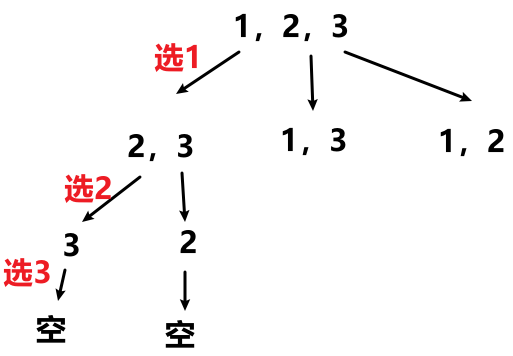
- 每层递归从剩余值中选一个,退出递归返回上一层需要回溯选中值。
- 时间复杂度:遍历节点个数,n+nx(n-1)+...n! = O(n!);叶子节点即 n! 种情况,需要复制 n!xn次。O(nxn!)。
- 空间复杂度:递归深度,即树高,O(n)。
3、代码
java
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<Integer> tmp = new ArrayList<>(); // 暂存已经选中的值
List<List<Integer>> ret = new ArrayList<>(); // 存放结果
permute(nums, tmp, ret);
return ret;
}
public void permute(int[] nums, List<Integer> tmp, List<List<Integer>> ret) {
// 结束递归:如果数组中的值都被选了,得到一个结果
if (tmp.size() == nums.length) {
ret.add(new ArrayList<Integer>(tmp));
return;
}
// 遍历元素
for (int i = 0; i < nums.length; i++) {
// 判断该元素是否被选中过
int j = 0;
for (; j < tmp.size(); j++) {
if (tmp.get(j) == nums[i]) break; // 该元素被选中过
}
// 该元素没有被选中过,就可以选
if (j == tmp.size()) {
tmp.add(nums[i]);
permute(nums, tmp, ret);
tmp.remove(tmp.size()-1); // 回到该层,撤销选中
}
}
}
}三、电话号码的字母组合
1、题目

2、分析
示例1:
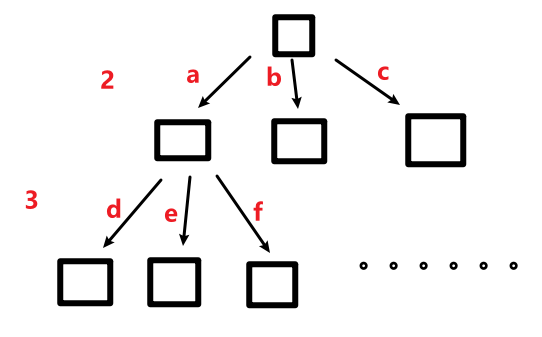
- 每递归一层,在数字对应的字母集合中选择一个字母,放入临时字母组合,继续递归。
- 递归完了,回到当前层,撤销选择,即把临时字母组合中选择的字母删除。继续选择数字对应的字母集合中的下一个字母。
- 时间复杂度:深度优先搜索,最多遍历 4+4^2+...+4^n 个节点;最多有 4^n 种组合,每种组合需要复制 n 次放入结果集。O(4+4^2+...+4^n+n*4^n) = O(n*4^n)。
- 空间复杂度:递归深度,即树高,O(n)。
3、代码
java
class Solution {
public List<String> letterCombinations(String digits) {
List<String> ret = new ArrayList<>(); // 存放结果
StringBuilder tmp = new StringBuilder(); // 暂存字母组合
Map<Character, String> map = new HashMap<>(); // 存放数字和字母集合的映射
map.put('2', "abc");
map.put('3', "def");
map.put('4', "ghi");
map.put('5', "jkl");
map.put('6', "mno");
map.put('7', "pqrs");
map.put('8', "tuv");
map.put('9', "wxyz");
letterCombinations(digits ,ret, tmp, 0, map);
return ret;
}
public void letterCombinations(String digits, List<String> ret, StringBuilder tmp, int index, Map<Character, String> map) {
// 递归结束条件:找到一个字母组合,放入结果集
if (digits.length() == tmp.length()) {
ret.add(new String(tmp.toString()));
return;
}
// 遍历当前层数字,对应的字母集合,选中
for (char ch : map.get(digits.charAt(index)).toCharArray()) { // String没有实现 Iterable 接口,先转成数组
tmp.append(ch); // 选中
letterCombinations(digits, ret, tmp, index+1, map); // 递归,在下一个号码中选
tmp.deleteCharAt(tmp.length()-1); // 撤销选中
}
}
}四、组合总和
1、题目

2、分析
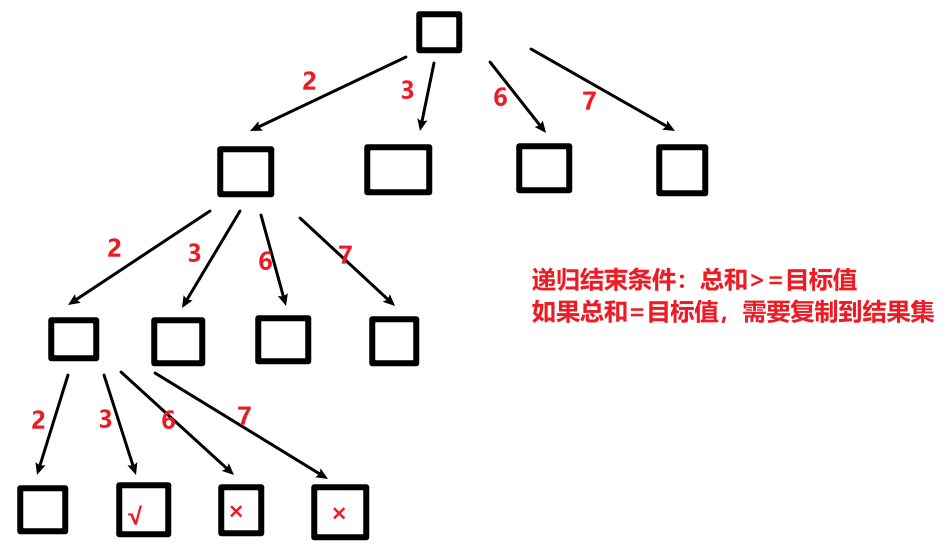
- 结束递归返回到当前层,需要撤销临时集合中的选中,并撤销总和中的计数。
- 剪纸操作:2,3 和 3,2 是一样的,因此选了 3 过后,不能再回头选 2。即每个节点只能选自身和之后的数。如:选了6后,后续只能选 6、7。
- 空间复杂度:递归深度,最差为 O(target),重复选 target 次 1。
3、代码
java
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<Integer> tmp = new ArrayList<>(); // 暂存一条结果
List<List<Integer>> ret = new ArrayList<>(); // 存储最终结果
int sum = 0; // 总和
combinationSum(candidates, target, tmp, ret, sum, 0);
return ret;
}
public void combinationSum(int[] candidates, int target, List<Integer> tmp, List<List<Integer>> ret, int sum, int index) {
// 如果总和等于目标值,存储一个结果并返回
// 如果总和大于目标值,直接返回
if (sum >= target) {
if (sum == target) ret.add(new ArrayList<Integer>(tmp));
return;
}
// 遍历 index 及其之后的数组,表示选中
for (int i = index; i < candidates.length; i++) {
// 选中
tmp.add(candidates[i]);
sum += candidates[i];
System.out.println(tmp);
combinationSum(candidates, target, tmp, ret, sum, i);
// 撤销选中
tmp.remove(tmp.size() - 1);
sum -= candidates[i];
}
}
}五、括号生成
1、题目

2、分析
- n对括号,左括号不能超过n**(剪枝1)** ,现有右括号个数不能超过左括号个数(否者右括号与左括号不匹配)(剪枝2)。
- 深度递归,两个分支,选左括号、选右括号。
- 时间复杂度:叶子节点个数(方案数)x复制的路径长度n,不考虑剪枝的情况(右括号个数<=左括号个数),2n个位置选n个位置放左括号,O(n*C(2n, n))。
- 空间复杂度:O(2*n)=O(n)。
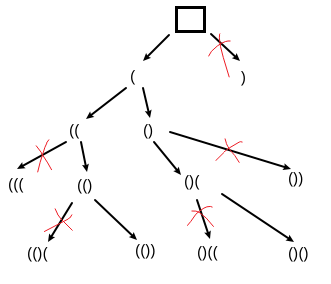
- 递归结束条件:右括号数=n,左括号数必=n,得到一个答案。
3、代码
java
class Solution {
public List<String> generateParenthesis(int n) {
char[] tmp = new char[2*n]; // 暂存结果
List<String> ret = new ArrayList<>(); // 存结果
generateParenthesis(tmp, ret, n, 0, 0); // 0,0 表示tmp填入的左、右括号个数
return ret;
}
public void generateParenthesis(char[] tmp, List<String> ret, int n, int left, int right) {
// 右括号达到n个,左括号比达到n个,找到一个结果
if (right == n) {
ret.add(new String(tmp));
return;
}
// 剪枝1,左括号个数不能超过n
if (left < n) {
tmp[left+right] = '(';
generateParenthesis(tmp, ret, n, left+1, right);
// 不用回溯,后面直接被覆盖
}
// 剪枝2,右括号个数不能超过左括号个数
if (right < left) {
tmp[left+right] = ')';
generateParenthesis(tmp, ret, n, left, right+1);
}
}
}六、单词搜索
1、题目

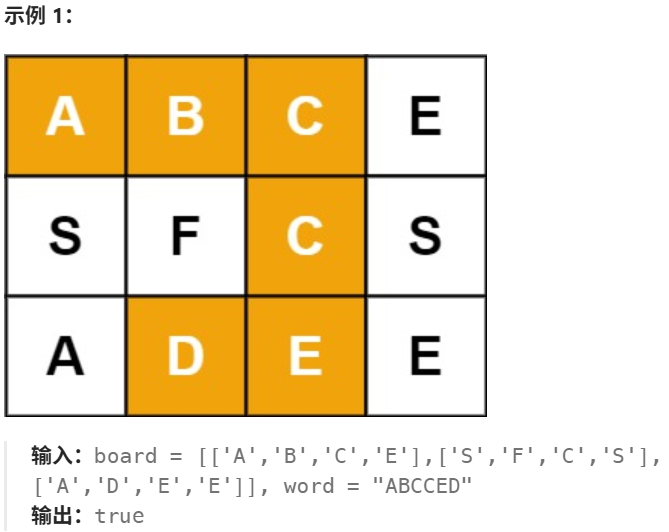
2、分析
- 以棋盘中的每个节点作为开头,开始深度递归。
- 每深入一层,就遍历一个word字母。如果匹配,则继续递归;如果不匹配,返回 false。如果四周都不匹配,最终返回 false,以下一个节点为开头匹配 word。
- 检测四周前,需要标记当前节点已经匹配过(设置为 0),避免被重复匹配。四周检测完后,如果都不匹配返回 flase,当前节点需要恢复原值,供下一个节点为开头的搜索使用。
优化:
- 如果word中的某种字母个数比棋盘中的个数多,那说明肯定不匹配。
- 如果word结尾字母在棋盘中的个数,比word开头字母在棋盘中的个数少,可以倒置word,让深度搜索的次数减少。
- 时间复杂度:m*n次深度搜索,每次深度搜索深度k,每层搜索3个节点(排除已匹配过的节点),O(m*n+k^3)。
- 空间复杂度:用于统计棋盘、word每种字母个数:2*128;递归深度:k。O(2*128+k)。
3、代码
java
class Solution {
// 相对移动坐标
public static final int[][] DIRS = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
public boolean exist(char[][] board, String word) {
// 统计棋盘每种字母个数
int[] boardNum = new int[128];
for (int i = 0; i < board.length; i++)
for (int j = 0; j < board[i].length; j++)
boardNum[board[i][j]]++;
// 优化1:word中某种字母数 > 棋盘中字母数,直接不匹配
int[] wordNum = new int[128];
char[] wordArray = word.toCharArray();
for (char ch : wordArray)
if (++wordNum[ch] > boardNum[ch]) return false;
// 优化2:word结尾字母在棋盘中的个数 < word开头字母在棋盘中的个数,倒置wordArray
if (wordNum[wordArray[0]] > wordNum[wordArray[wordArray.length-1]])
wordArray = new StringBuilder(word).reverse().toString().toCharArray();
// 以棋盘中的每个字母为开头,进行深搜
for (int i = 0; i < board.length; i++)
for (int j = 0; j < board[i].length; j++)
if (exist(board, wordArray, i, j, 0))
return true; // 找到一个匹配结果,存在
return false;
}
public boolean exist(char[][] board, char[] word, int i, int j, int k) {
// 不匹配,结束递归
if (board[i][j] != word[k]) return false;
// 整个word都匹配,结束递归,存在
if (k == word.length-1) return true;
// 继续深搜,先标记当前节点已经匹配过,不能重复匹配
board[i][j] = 0;
// 深搜四周,不能是被匹配过的,不能超过棋盘边界
for (int m = 0; m < DIRS.length; m++) {
int tmpi = i+DIRS[m][0];
int tmpj = j+DIRS[m][1];
if (tmpi >= 0 && tmpi < board.length && tmpj >= 0 && tmpj < board[0].length && exist(board, word, tmpi, tmpj, k+1))
return true;
}
// 四周都不匹配,返回 false。需要恢复当前节点的原值,以供下一个棋盘节点开头的深搜重用
board[i][j] = word[k];
return false;
}
}七、分割回文串
1、题目

2、分析
- 对于以s[i]为结尾,有分割、不分割两种分支选择。若选分割,则要判断分割出的这个子串是否是回文串。如果是则分割加入结果,并更新 start 和 i;如果不是,不做处理。继续递归。
- 递归完后,需要回溯,撤销本层分割出的子串。
- 如果s[i]是s的最后一个字母,则必是分割位置,只能选分割。
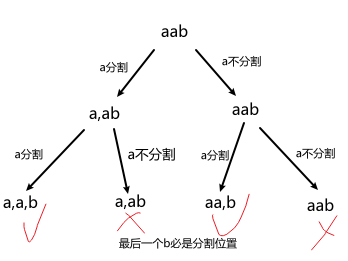
- 时间复杂度:搜索 1+2+...+2^(n-1)=2^n-1个节点。每条路径(共 2^(n-1) 个叶子节点),判断是否是回文串+结果 2n。O(2^n-1 + 2*n*2^(n-1) ) = O(n*2^n)
- 空间复杂度:递归深度,字符串长度n,O(n)。
3、代码
java
class Solution {
public List<List<String>> partition(String s) {
List<String> tmp = new ArrayList<>(); // 暂存结果
List<List<String>> ret = new ArrayList<>(); // 返回结果
partition(s, tmp, ret, 0, 0); // 0,0 表示子串起点、分割位置
return ret;
}
public void partition(String s, List<String> tmp, List<List<String>> ret, int start, int i) {
// s 遍历完了,找到一种结果
if (i == s.length()) {
ret.add(new ArrayList<String>(tmp));
return;
}
// 选择不分割,直接递归下个位置(最后一个位置必须是分割)
if (i < s.length()-1) partition(s, tmp, ret, start, i+1);
// 选择分割,先判断是否是回文串,再分割
// 如果分割,需要更新 start 再递归,递归完了需要回溯,撤销掉分割
if (palindrome(s, start, i)) {
tmp.add(s.substring(start, i+1));
partition(s, tmp, ret, i+1, i+1);
tmp.removeLast(); // 回溯
}
}
public boolean palindrome(String s, int left, int right) {
while (left < right) {
if (s.charAt(left++) != s.charAt(right--)) return false;
}
return true;
}
}八、N皇后
1、题目

2、分析
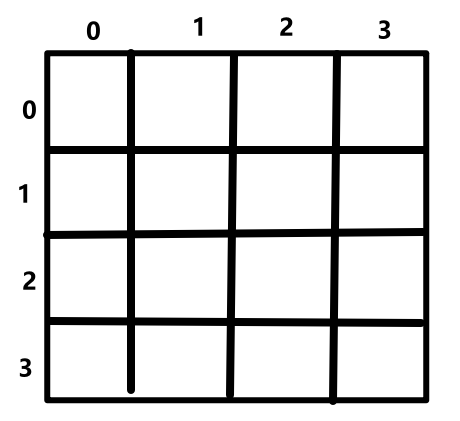
- 数组 tmp[i] 表示皇后坐标 (i, tmp[i])。每深入一层就代表下一行,行必不冲突 。新放的皇后必须保证列不冲突 。那么需要一个 col 布尔类型数组标记某一列是否被占用。
- 要保证斜线不冲突 ,↙不冲突,即 行+列 不冲突;↘不冲突,即 行-列 不冲突,用额外的 flag1(n=4时,0~6,数组长度2n-1)、flag2(n=4时,-3~3,需要加n-1=3让下标变为正整数 ,0~6,数组长度2n-1)数组标记。
- 递归结束条件:递归到第 n 层(0~n-1行的皇后已经全部找到),把 tmp 数组转换为一个结果。
- 回溯:返回到上一行前,需要把这一行在 col、flag1、flag2 的占用标记撤销掉。
- 时间复杂度:结果数=叶子结点数=第一层n种选择xn-1x......x1=n!(没有这么多,因为有些结果不满足不冲突的条件),每种结果复制成答案,需要遍历每行的每列,n^2。O(n!*n^2)
- 空间复杂度:tmp、col 占 2n,falg1、flag2 占 2(2n-1),递归深度 n。O(n)
3、代码
java
class Solution {
public List<List<String>> solveNQueens(int n) {
int[] tmp = new int[n]; // 存坐标 (i, tmp[i])
boolean[] col = new boolean[n]; // 用于判断 tmp[i] 列是否冲突
boolean[] flag1 = new boolean[2*n-1]; // 用于判断 i+tmp[i] 是否冲突
boolean[] flag2 = new boolean[2*n-1]; // 用于判断 i-tmp[i]+n-1 是否冲突
List<List<String>> ret = new ArrayList<>(); // 存放最终结果
dfs(n, 0, tmp, col, flag1, flag2, ret);
return ret;
}
public void dfs(int n, int i, int[] tmp, boolean[] col, boolean[] flag1, boolean[] flag2, List<List<String>> ret) {
// 已经放完皇后,复制结果,并结束递归
if (i == n) {
char[] str = new char[n];
List<String> strList = new ArrayList<>();
for (int j = 0; j < n; j++) { // 生成n行字符串
Arrays.fill(str, '.'); // 填充 .
str[tmp[j]] = 'Q'; // 对应列放置皇后
strList.add(new String(str)); // 添加该行的结果
}
ret.add(strList);
return;
}
// 如果当前行的皇后位置 j 不冲突(列、斜线),则放置,继续放下一行
for (int j = 0; j < n; j++) {
if (!col[j] && !flag1[i+j] && !flag2[i-j+n-1]) {
// 放置
tmp[i] = j;
col[j] = true;
flag1[i+j] = true;
flag2[i-j+n-1] = true;
// 继续放下一行
dfs(n, i+1, tmp, col, flag1, flag2, ret);
// 撤销放置,tmp 不用撤销,会直接覆盖
col[j] = false;
flag1[i+j] = false;
flag2[i-j+n-1] = false;
}
}
}
}