【节点】[Constant节点]原理解析与实际应用

【Unity Shader Graph 使用与特效实现】专栏-直达

在Unity的Shader Graph可视化着色器编辑器中，Constant节点是一个基础但至关重要的数学工具节点。它允许开发者在着色器程序中预定义和使用常见的数学常量值，无需手动输入这些数值，从而提高开发效率和代码的准确性。

Constant节点概述

Constant节点属于Shader Graph中的数学工具类节点，专门用于提供精确的数学常量值。在图形编程和着色器开发中，精确的数学常量对于实现各种视觉效果至关重要，从简单的颜色计算到复杂的物理模拟都离不开这些基础数值。

节点特性

Constant节点具有以下几个显著特点：

提供预定义的数学常量，确保数值精度
简化着色器代码，避免手动输入可能导致的错误
支持多种常用数学常量，覆盖大多数图形编程需求
输出为浮点数值，兼容各种着色器计算

应用场景

Constant节点在Shader Graph中的应用非常广泛：

圆形和弧形计算中的π值使用
周期性动画和波动效果中的τ值应用
美学比例计算中的黄金分割φ值
自然增长和衰减模拟中的自然常数e
距离计算和标准化处理中的√2值

端口详解

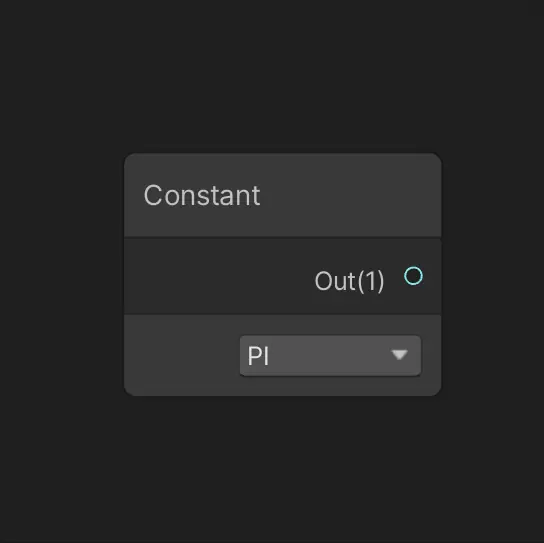
Constant节点仅包含一个输出端口，设计简洁但功能专一。

输出端口

名称：Out

方向：输出

类型：Float

绑定：无

描述：输出当前选择的数学常量值

输出端口的特点：

始终输出浮点数类型的常量值
数值精度满足图形计算需求
可以直接连接到其他节点的输入端口
支持实时预览当前选择的常量值

控件配置

Constant节点提供了一个下拉选单控件，用于选择所需的数学常量类型。

Mode下拉选单

Mode控件决定了节点输出的具体数学常量值，包含以下五个选项：

PI - 圆周率π

数值：约等于3.1415926
应用：圆形计算、角度转换、周期性函数

TAU - 圆周率的两倍τ

数值：约等于6.28318530
应用：完整的圆周弧度、简化角度计算

PHI - 黄金比例φ

数值：约等于1.618034
应用：美学比例、自然生长模式、艺术构图

E - 自然常数e

数值：约等于2.718282
应用：指数增长、衰减过程、概率计算

SQRT2 - 2的平方根

数值：约等于1.414214
应用：对角线距离、标准化计算、几何变换

数学常量深度解析

PI（圆周率）

圆周率π是数学中最著名的常数之一，代表圆的周长与直径的比值。

数学定义：

π = 周长 / 直径 ≈ 3.141592653589793

在Shader Graph中的应用：

角度与弧度转换

ini 复制代码

// 角度转弧度
radians = degrees * PI / 180.0

// 弧度转角度
degrees = radians * 180.0 / PI

圆形和弧形计算

scss 复制代码

// 圆形坐标计算
float2 circlePosition = float2(cos(angle * PI * 2.0), sin(angle * PI * 2.0))

// 圆弧长度
float arcLength = radius * centralAngle * PI / 180.0

周期性函数

scss 复制代码

// 正弦波动
float wave = sin(time * PI * 2.0)

// 圆形渐变
float circularGradient = length(uv - 0.5) * PI

TAU（2π常数）

TAU是圆周率的两倍，代表完整的圆周弧度，在某些情况下可以简化数学表达式。

数学定义：

τ = 2π ≈ 6.283185307179586

在Shader Graph中的应用：

完整的周期计算

scss 复制代码

// 使用TAU的完整周期正弦波
float sineWave = sin(time * TAU)

// 圆形遍历
for(float i = 0.0; i < TAU; i += 0.1) {
    // 圆形采样点
}

简化角度计算

arduino 复制代码

// 传统方式
float radians = degrees * PI / 180.0

// 使用TAU方式（概念上更清晰）
float radians = degrees * TAU / 360.0

PHI（黄金比例）

黄金比例φ是一个无理数，在艺术、建筑和自然界中广泛存在，被认为具有美学上的完美比例。

数学定义：

φ = (1 + √5) / 2 ≈ 1.618033988749895

在Shader Graph中的应用：

美学比例布局

arduino 复制代码

// 黄金比例分割
float goldenSection = totalLength / PHI

// 黄金矩形比例
float goldenRectangleWidth = height * PHI

自然生长模式模拟

scss 复制代码

// 斐波那契螺旋
float spiralRadius = baseRadius * pow(PHI, angle / (PI * 2.0))

颜色和亮度分布

scss 复制代码

// 基于黄金比例的亮度衰减
float brightness = baseBrightness / pow(PHI, distance)

E（自然常数）

自然常数e是自然对数函数的底数，在指数增长和衰减过程中具有重要地位。

数学定义：

e = lim(1 + 1/n)ⁿ ≈ 2.718281828459045

在Shader Graph中的应用：

指数衰减效果

scss 复制代码

// 自然衰减
float decay = pow(E, -decayRate * time)

// 平滑过渡
float smoothTransition = 1.0 - pow(E, -transitionSpeed * factor)

概率分布模拟

arduino 复制代码

// 正态分布近似
float gaussian = pow(E, -0.5 * pow((x - mean) / deviation, 2.0))

生长过程模拟

scss 复制代码

// 指数增长
float growth = initialValue * pow(E, growthRate * time)

SQRT2（2的平方根）

2的平方根是对角线与边长的比值，在距离计算和标准化中非常有用。

数学定义：

√2 ≈ 1.4142135623730951

在Shader Graph中的应用：

对角线距离计算

arduino 复制代码

// 最大可能距离（正方形中对角线）
float maxDistance = diagonalLength / SQRT2

// 标准化处理
float normalizedValue = rawValue / SQRT2

纹理采样偏移

ini 复制代码

// 对角线方向采样
float2 diagonalOffset = float2(1.0, 1.0) * offsetAmount / SQRT2

实际应用示例

圆形进度条实现

使用PI常量创建平滑的圆形进度指示器：

ini 复制代码

HLSL

// 在Fragment Shader中
void surf(Input IN, inout SurfaceOutputStandard o)
{
    // 计算UV坐标到圆心的距离和角度
    float2 centeredUV = IN.uv_MainTex - 0.5;
    float angle = atan2(centeredUV.y, centeredUV.x);
    float radius = length(centeredUV) * 2.0;

    // 使用PI进行角度标准化
    float normalizedAngle = (angle + PI) / (2.0 * PI);

    // 进度计算（0到1范围）
    float progress = _Progress;

    // 绘制圆形进度条
    if (radius <= 1.0 && radius >= 0.8 && normalizedAngle <= progress) {
        o.Albedo = _ProgressColor;
    } else {
        o.Albedo = _BaseColor;
    }
}

波动动画效果

利用TAU创建流畅的波动动画：

arduino 复制代码

HLSL

// 波动效果实现
float waveEffect(float2 position, float time)
{
    // 使用TAU简化完整周期计算
    float wave1 = sin(position.x * _Frequency + time * TAU) * _Amplitude;
    float wave2 = sin(position.y * _Frequency + time * TAU + PI * 0.5) * _Amplitude;

    return (wave1 + wave2) * 0.5;
}

黄金比例布局系统

基于PHI创建视觉上和谐的UI元素布局：

ini 复制代码

HLSL

// 黄金比例布局计算
float2 goldenRatioLayout(float2 screenSize, int elementIndex)
{
    float totalHeight = screenSize.y;
    float sectionHeight = totalHeight / PHI;

    float yPosition = 0.0;
    for(int i = 0; i < elementIndex; i++) {
        yPosition += sectionHeight;
        sectionHeight /= PHI; // 每个部分按黄金比例缩小
    }

    return float2(screenSize.x * 0.5, yPosition);
}

性能优化建议

常量值的优化使用

预计算组合常量：将常用的常量组合预先计算并存储

ini 复制代码

// 优化前
float result = inputValue * PI * 2.0;

// 优化后
float result = inputValue * TAU; // 使用预定义的TAU常量

避免重复计算：在Sub Graph中封装常用常量操作

arduino 复制代码

// 创建角度转换Sub Graph
// 输入：角度值，输出：弧度值
// 内部使用：PI / 180.0 的预计算常量

节点连接优化

减少重复Constant节点：相同常量值应共享节点实例
合理组织节点结构：将常量计算集中管理，提高可读性和性能
使用Sub Graph封装：将复杂的常量相关计算封装为可重用组件

高级技巧与最佳实践

自定义常量扩展

虽然Constant节点提供的是固定常量，但可以通过数学运算创建派生常量：

ini 复制代码

// 创建半PI常量
float halfPI = PI * 0.5;

// 创建四分之一PI常量
float quarterPI = PI * 0.25;

// 创建黄金比例的倒数
float inversePHI = 1.0 / PHI;

精度控制技巧

在不同精度需求场景下的使用方法：

高精度计算：直接使用Constant节点提供的值
性能敏感场景：考虑使用近似值或查找表
移动端优化：评估是否真的需要全精度常量

调试与验证

确保常量使用正确的调试方法：

使用Preview节点实时查看常量输出
通过颜色编码可视化常量值的分布
建立测试用例验证常量计算的准确性

常见问题解答

精度相关问题

问：Constant节点提供的常量值精度足够吗？

答：对于绝大多数图形应用，Constant节点提供的精度完全足够。只有在极端科学计算或金融应用场景下才需要考虑更高精度。

问：如何验证常量值的准确性？

答：可以通过创建简单的测试Shader来验证，比如使用PI计算圆的面积并与理论值比较。

性能相关问题

问：在Shader中使用Constant节点会影响性能吗？

答：Constant节点在编译时会被替换为具体的数值常量，运行时没有性能开销。

问：应该为每个常量创建单独的节点吗？

答：不需要，相同值的常量应该共享节点实例，不同值的常量才需要分别创建。

应用相关问题

问：什么时候应该使用TAU而不是PI？

答：当计算涉及完整周期（360度或2π弧度）时，使用TAU可以使表达式更简洁直观。

问：黄金比例在游戏开发中的实际价值是什么？

答：黄金比例可以帮助创建视觉上更和谐的比例关系，在UI设计、关卡布局、角色比例等方面都有应用价值。

【Unity Shader Graph 使用与特效实现】专栏-直达 （欢迎点赞留言探讨，更多人加入进来能更加完善这个探索的过程，🙏）