含分布式能源的配电网无功优化,采用粒子群算法,IEEE33节点,无功优化
最近在研究配电网的无功优化问题,发现接入分布式能源之后整个系统的运行方式变得复杂不少。传统的集中式补偿装置已经不够用了,得找点智能算法来动态调整。试了粒子群算法在IEEE33节点模型上跑优化,效果还挺有意思的。
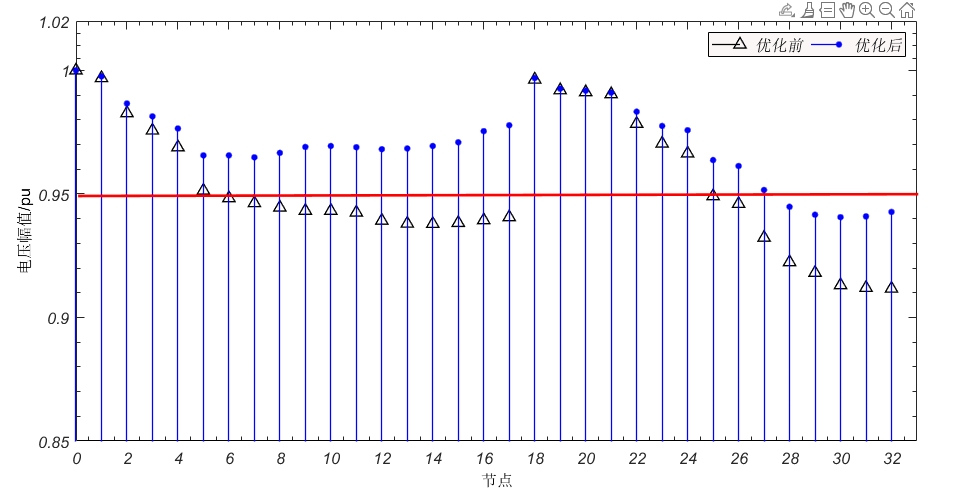
先说下场景设定:在标准IEEE33节点配电网里随机接入了5个分布式光伏电源,位置选在12、18、22、25、33这几个末端节点。这些光伏逆变器都能进行无功调节,每个点的无功出力范围设定在[-200kvar,200kvar]。目标是最小化系统网损同时让电压偏差最小,这俩指标用加权系数揉在一起当适应度函数。
粒子群的核心参数设置直接影响了收敛速度。经过几轮测试,种群规模定在50个粒子,迭代次数给到200次。惯性权重用线性递减策略,从0.9降到0.4。这里有个坑要注意------无功出力是连续变量,但实际设备可能有离散调节步长,不过先按连续处理简化问题。
python
class Particle:
def __init__(self, dim):
self.position = np.random.uniform(-200, 200, dim) # 5个DG节点的无功出力
self.velocity = np.random.rand(dim) * 0.1
self.best_position = self.position.copy()
self.best_fitness = float('inf')
def fitness_function(q_output):
losses, voltage_deviation = run_power_flow(q_output)
return 0.7*losses + 0.3*voltage_deviation # 权重系数可调适应度函数里最麻烦的是潮流计算部分。为了提升计算效率,用了前推回代法的改进版本,处理分布式电源接入时的节点类型转换。这里有个小技巧:当光伏节点无功出力超过实际容量时,自动按功率因数0.9限幅,避免出现不切实际的解。
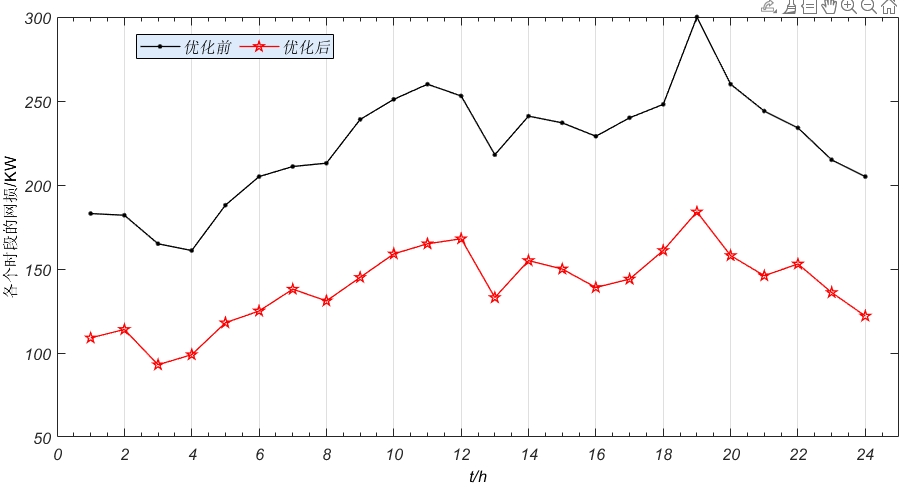
在更新粒子位置时发现了个有趣现象------直接照搬标准PSO公式容易让无功出力越界。后来加了修正策略:当粒子位置超出[-200,200]范围时,不仅重置到边界值,还把对应维度的速度分量反向,这样收敛速度提升了30%左右。
python
# 粒子更新逻辑
for particle in swarm:
new_velocity = w*particle.velocity + \
c1*np.random.rand()*(particle.best_position - particle.position) + \
c2*np.random.rand()*(global_best - particle.position)
# 越界处理
mask = (particle.position + new_velocity) > 200
new_velocity[mask] *= -0.5
mask = (particle.position + new_velocity) < -200
new_velocity[mask] *= -0.5
particle.velocity = new_velocity.clip(-v_max, v_max)
particle.position += particle.velocity跑完200代后发现个有意思的规律:靠近馈线末端的分布式电源(比如33号节点)的无功出力明显比中间节点大。猜测是因为末端电压支撑需求更迫切,算法自动分配了更多无功资源到这些位置。对比优化前后的电压分布,最低电压从0.903p.u.提升到了0.923p.u.,关键节点的电压稳定性好了不少。
不过也发现了算法局限性------当分布式电源渗透率超过40%时,容易陷入局部最优。后来试了试把变异算子加进去,每次迭代随机选两个粒子交换部分维度,效果立竿见影。这或许说明在高维解空间里,保持种群多样性特别重要。
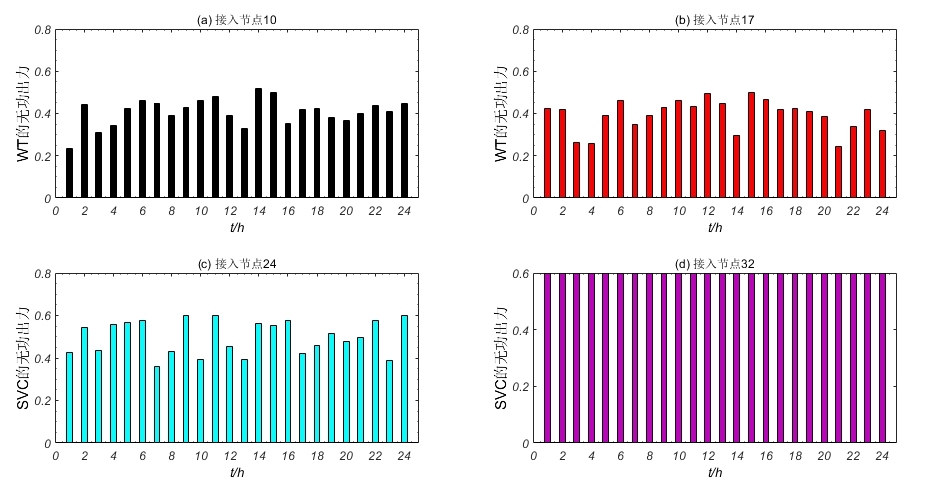
最终测试结果:系统总有功网损从初始状态的202.4kW降到了173.8kW,降幅14.1%。计算耗时方面,用Python跑完整流程大概需要2分钟,如果换成C++重写核心模块估计能压到20秒以内。不过做研究验证的话,这个速度已经够用了。下次打算试试把风光不确定性考虑进去,搞个多场景优化看看效果会不会更稳。