Qwen GSPO算法的深入学习和理解

文章目录

参考论文和资料
[一从PPO和GRPO到GSPO](#一从PPO和GRPO到GSPO)
- [1.1 自回归语言模型强化学习基础](#1.1 自回归语言模型强化学习基础)
- [1.2 PPO算法](#1.2 PPO算法)
- [1.3 GRPO算法](#1.3 GRPO算法)
- [1.4 GRPO根本性问题与反思](#1.4 GRPO根本性问题与反思)
- [1.5 GSPO算法](#1.5 GSPO算法)
- [1.6 GSPO稳定性分析](#1.6 GSPO稳定性分析)
- [1.7 补充：类REINFORCE形态](#1.7 补充：类REINFORCE形态)
- [1.8 PPO、GRPO与GSPO对比](#1.8 PPO、GRPO与GSPO对比)
[二 GSPO-Token:GSPO的token-level变体](#二 GSPO-Token:GSPO的token-level变体)
- [2.1 GSPO-Token梯度推导](#2.1 GSPO-Token梯度推导)
- [2.2 GSPO的优势](#2.2 GSPO的优势)
- - [2.2.1 GSPO在MoE训练中的优势](#2.2.1 GSPO在MoE训练中的优势)
  - [2.2.2 GSPO在基础设施中的优势](#2.2.2 GSPO在基础设施中的优势)
[三总结](#三总结)

参考论文和资料

一从PPO和GRPO到GSPO

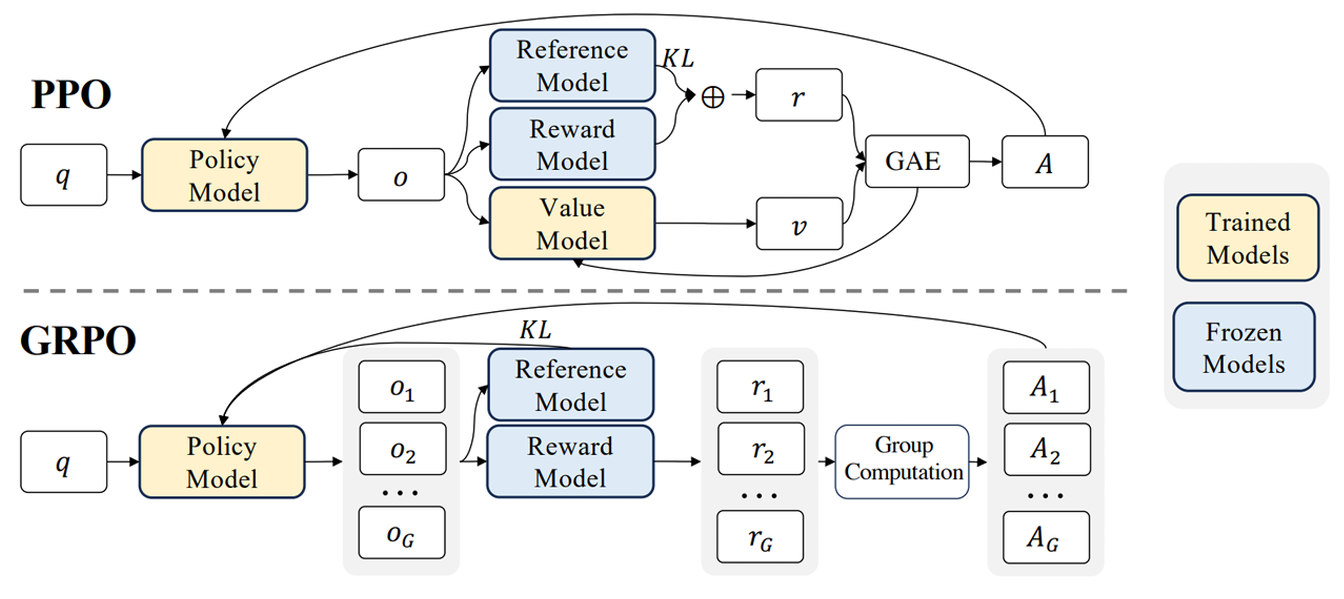
LLM的RL阶段主流的算法包括PPO（ProximalPolicyOptimization）、GRPO（GroupRelativePolicyOptimization）算法以及它们的改进品。
本章内容所使用的公式按照DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models中的描述，Group Sequence Policy Optimization中的公式关于PPO和GSPO的表述有所不同，但是不影响后续的理解。

1.1 自回归语言模型强化学习基础

自回归语言模型（autoregressive LM）参数为 θ \theta θ，对应策略为（policy） π θ \pi_\theta πθ。输入（query）为 x ∈ D x \in D x∈D，模型针对每个 x x x生成响应（response） y y y。

上下文处理机制：大模型本身无显式记忆功能，需通过外部机制（如历史对话打包）将上下文信息作为输入。然而，这受限于模型的上下文窗口大小（context window），因此提升输入上限是持续的研究方向。

y y y 的似然函数(输出每个token的条件概率连乘)为： π θ ( y ∣ x ) = ∏ t = 1 ∣ y ∣ π θ ( y t ∣ x , y < t ) \pi_\theta(y \mid x) = \prod_{t=1}^{|y|} \pi_\theta(y_t \mid x, y_{<t}) πθ(y∣x)=∏t=1∣y∣πθ(yt∣x,y<t)。给定 ( x , y ) (x, y) (x,y)，由外部评分器（verifier） r ( x , y ) r(x, y) r(x,y) 给出奖励，范围在 [ 0 , 1 ] [0, 1] [0,1]。
RL 目标：最大化期望奖励 ------PPO、GRPO、GSPO 优化目标的基础。 π θ \pi_\theta πθ 是语言模型的生成分布； r {r} r 是任务相关的打分函数（如人类偏好、正确率）。
max ⁡ θ E x , y ∼ π θ [ r ( x , y ) ] \max_\theta \mathbb{E}{x, y \sim \pi\theta} [r(x, y)] θmaxEx,y∼πθ[r(x,y)]
大模型强化学习训练实质上就是调整 π θ \pi_\theta πθ，让它更倾向生成高分响应。

1.2 PPO算法

PPO的做法是使用价值函数评估生成的响应中乜咯标记的质量，然后比较新旧策略模型，如果变化过大，阶段更新，保证模型以小幅度持续向目标方向优化。
PPO的目标函数如下：
J P P O ( θ ) = E [ q ∼ P ( Q ) , o ∼ π θ o l d ( O ∣ q ) ] 1 ∣ o ∣ ∑ t = 1 ∣ o ∣ min ⁡ [ π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) A t , clip ( π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) , 1 − ϵ , 1 + ϵ ) A t ] \mathcal{J}{PPO}(\theta) = \mathbb{E}[q \sim P(Q), o \sim \pi{\theta_{old}}(O|q)] \frac{1}{|o|} \sum_{t=1}^{|o|} \min \left[ \frac{\pi_{\theta}(o_t|q, o_{<t})}{\pi_{\theta_{old}}(o_t|q, o_{<t})} A_t, \text{clip}\left( \frac{\pi_{\theta}(o_t|q, o_{<t})}{\pi_{\theta_{old}}(o_t|q, o_{<t})}, 1-\epsilon, 1+\epsilon \right) A_t \right] JPPO(θ)=E[q∼P(Q),o∼πθold(O∣q)]∣o∣1t=1∑∣o∣min[πθold(ot∣q,o<t)πθ(ot∣q,o<t)At,clip(πθold(ot∣q,o<t)πθ(ot∣q,o<t),1−ϵ,1+ϵ)At]
重要性比率 ： r t ( θ ) = π θ ( o t ∣ o < t ) π θ old ( o t ∣ o < t ) r_t(\theta) = \frac{\pi_{\theta}(o_t|o_{<t})}{\pi_{\theta_{\text{old}}}(o_t|o_{<t})} rt(θ)=πθold(ot∣o<t)πθ(ot∣o<t)，衡量新策略在当前位置 t t t生成 o t o_t ot的概率， ϵ \epsilon ϵ 是重要性比率的裁剪范围。如果一个动作在新策略出现变得可能出现，它的重要性比率（ r t ( θ ) r_t(\theta) rt(θ)）就大于1，否则小于1。通过重要性比率，PPO利用旧数据安全地更新模型。
优势函数 A t A_t At由价值函数（Value Model）进行估计，使用GAE(Generalized Advantage Estimation)近似得到。
PPO的优化逻辑：在token级别进行执行优化，每个token优势（Advantage）依赖价值模型，训练时对所有 t t t的梯度求平均，实现稳定的策略更新。
进行---
PPO 的架构局限：价值模型的长文本瓶颈。PPO 的训练范式依赖于一个额外的价值模型，通过预测未来期望回报来校准原始奖励，从而生成更具信息量的 Advantage 信号以稳定训练。
Token级价值估计的局限性 ：这种机制在处理长文本时存在显著的归纳偏置问题 。
- 语义割裂： 语言具有极强的非线性组合特征，单个 Token 可能彻底翻转序列的情感极性或核心含义。
- 分配谬误： 价值函数试图基于局部粒度分配价值，忽略了上下文的连贯性和全局依赖，导致在长序列场景下泛化能力不足。

1.3 GRPO算法

GRPO（GroupRelativePolicyOptimization）算法的设计思想：采样多次，直接用奖励模型的平均值充当优势（Advantage），替代价值模型来的绝对分值，极大减少算力资源的消耗。
GRPO目标函数：
J G R P O ( θ ) = E [ q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ o l d ( O ∣ q ) ] 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ { min ⁡ [ π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) A ^ i , t , clip ( π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) , 1 − ϵ , 1 + ϵ ) A ^ i , t ] − β D K L [ π θ ∣ ∣ π r e f ] } \mathcal{J}{GRPO}(\theta) = \mathbb{E}{[q \sim P(Q), \{o_i\}{i=1}^G \sim \pi{\theta_{old}}(O|q)]} \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left\{ \min \left[ \frac{\pi_{\theta}(o_{i,t}|q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q, o_{i,<t})} \hat{A}{i,t}, \text{clip}\left( \frac{\pi{\theta}(o_{i,t}|q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q, o_{i,<t})}, 1-\epsilon, 1+\epsilon \right) \hat{A}{i,t} \right] - \beta \mathbb{D}{KL}[\pi_{\theta}||\pi_{ref}] \right\} JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O∣q)]G1i=1∑G∣oi∣1t=1∑∣oi∣{min[πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^i,t,clip(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t),1−ϵ,1+ϵ)A^i,t]−βDKL[πθ∣∣πref]}
组相对优势（group-relative advantage）： A ^ i , t = r i − m e n ( r ) s t d ( r ) \hat A_{i,t}=\frac{r_i-men(r)}{std(r)} A^i,t=std(r)ri−men(r)。
GRPO的优化逻辑：
1. 采样：对每个query，生成多个响应 {o_1, ..., o_G}。
2. 奖励计算 ：对每个响应计算其原始奖励 r_i = r(x, o_i)
3. 优势计算（Advantage） ：使用奖励的z-score作为优势估计： A ^ i , t = r i − m e n ( r ) s t d ( r ) \hat A_{i,t}=\frac{r_i-men(r)}{std(r)} A^i,t=std(r)ri−men(r)
4. 重要性采样与裁剪：在每个token上独立计算重要性比率并做裁剪。
  clip ( π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) , 1 − ϵ , 1 + ϵ ) A ^ i \text{clip}\left(\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i,<t})}, 1-\epsilon, 1+\epsilon\right) \hat{A}_i clip(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t),1−ϵ,1+ϵ)A^i

search
<arg_key>query</arg_key>
<arg_value>离策略学习 off-policy learning definition importance sampling ratio sample distribution deviation</arg_value>
</tool_call>
离策略学习情境（off-policy learning setting）：在强化学习中，用于生成样本的策略（行为策略，behavior policy）与正在优化的目标策略（target policy）不一致。在这种情境下，样本分布与当前策略分布存在偏差，需要通过重要性采样等技术进行修正。PPO和GRPO通过裁剪机制来缓解这种偏差带来的负面影响，确保训练的稳定性。
在PPO和GRPO中，裁剪机制（clipping mechanism）的核心作用是控制重要性采样比（importance sampling ratio）的波动范围 ，防止因离策略样本分布与当前策略分布偏差过大导致的梯度估计不稳定。具体来说，当旧策略生成的样本与当前策略的采样行为差异过大时，重要性采样比会出现极端值，进而引发梯度爆炸或剧烈振荡。通过设置上下界（如 1 ± ϵ 1\pm \epsilon 1±ϵ），裁剪机制能够限制这些异常样本对梯度更新的影响，确保优化过程在策略空间中采取保守的局部调整，从而维持训练的稳定性和收敛性。

GRPO 的局限：Token 级粒度的噪声问题，裁剪机制可能放大噪声。GRPO 依然沿用 Token 级别的更新粒度：

精细化计算： 逐 Token 计算重要性权重并进行剪切。
信号分散： 学习信号分散在序列中，而非整体评估。

在 MoE 架构下的副作用： 当配合动态激活的 MoE 模型（尤其是长输出或大型稀疏模型）时，这种 Token 级噪声会被放大。各 Token 相互竞争积分，且专家激活不一致，导致学习结果模糊且不稳定。

1.4 GRPO根本性问题与反思

群体序列策略优化（Group Sequence Policy Optimization，GSPO）算法存在严重稳定性问题表现为训练不稳定，模型灾难性坍塌。
GRPO不稳定的根本原因在于：错误使用重要性采样权重（importancesamplingweights），导致训练过程中出现高方差噪声（high-variancenoise），随着响应长度（responselength）增加，噪声逐步积累，同时被裁剪机制（clipping）进一步放大。最终导致模型坍塌（collapse）。
重要性采样理论公式为：
E z ∼ π tar [ f ( z ) ] = E z ∼ π beh [ π tar ( z ) π beh ( z ) f ( z ) ] ≈ 1 N ∑ i = 1 N π tar ( z ) π beh ( z ) f ( z ) \mathbb{E}{z \sim \pi{\text{tar}}}[f(z)] = \mathbb{E}{z \sim \pi{\text{beh}}}\left[\frac{\pi_{\text{tar}}(z)}{\pi_{\text{beh}}(z)} f(z)\right] \approx \frac{1}{N} \sum_{i=1}^{N} \frac{\pi_{\text{tar}}(z)}{\pi_{\text{beh}}(z)} f(z) Ez∼πtar[f(z)]=Ez∼πbeh[πbeh(z)πtar(z)f(z)]≈N1i=1∑Nπbeh(z)πtar(z)f(z)
π t a r \pi_{tar} πtar是目标分布， π b e h \pi_{beh} πbeh是行为分布。通过加权修正行为分布样本点的偏差，以逼近目标分布的期望。其中的重要条件是需要通过对行为分布 π b e h \pi_{beh} πbeh进行多样本平均( N > > 1 N>>1 N>>1)保证加权修正生效。 原因是在大量样本的情况下，根据大数定理，平均值能够收敛到真实期望值，各样本的随机噪声可以被平均掉，如果样本很少的情况下，目标分布与行为分布的比值会处于计算状态（过大或过小），导致整体方差较高。
GRPO在每个token上计算重要性比率 r t ( θ ) = π θ ( o t ∣ o < t ) π θ old ( o t ∣ o < t ) r_t(\theta) = \frac{\pi_{\theta}(o_t|o_{<t})}{\pi_{\theta_{\text{old}}}(o_t|o_{<t})} rt(θ)=πθold(ot∣o<t)πθ(ot∣o<t)，每个token分布 π θ o l d ( . ∣ q , o i , < t ) \pi_{\theta_{old}}(. |q,o_i,<t) πθold(.∣q,oi,<t)是一个概率分布，但是GRPO只抽取一个样本（实际生成的token O i , t O_{i,t} Oi,t），没有进行任何平均处理，直接使用随机样本权重代表整个分布，结果 r i , t ( θ ) r_{i,t}(\theta) ri,t(θ)作为权重非常不稳定，方差极大，同时这种噪声在长序列中会积累，并被裁剪机制进⼀步放大，最终造成模型不可逆的崩溃（model collapse）。
一旦坍塌发生，即使恢复到先前的检查点（checkpoint）、精调超参数（如裁剪范围）、增加生成长度或更
换强化学习查询，训练仍无法恢复。

与PPO和GRPO这类基于token级重要性比率（import ratio）的算法不同，GSPO基于序列级似然函数（sequence likelihood）定义重要性比，并在序列层面执行裁剪（clipping）、奖励（rewarding）和优化（optimization）。
GSPO基于序列似然（sequencelikelihood）定义重要性比。通过归一化奖励（normalizedrewards）计算同一查询的多响应优势（advantage），实现序列级奖励与优化的对齐（alignment）。
GRPO的设计中token级重要性权重的失效揭示了一个原则：优化目标的"单位"应当与奖励的"单位"相匹配。 GRPO中奖励是序列级别，优化在token级别，存在错配问题，这种不匹配使得off-policy修正在token级别上没有意义，同时引入了噪声与不稳定性。
因此应该将重要性比率与优化目标转移到序列级别上（sequence-level），重新定义重要性权重，执行奖励归一化与优化。

1.5 GSPO算法

GSPO（Group Sequence Policy Optimization）的改进 ：GSPO 的核心变革在于将粒度提升至序列级别：

维度转换： 奖励不再是 Token 级，而是序列级。
全局计算： 重要性比率基于整个输出计算，剪切也在完整序列层面进行。
统一传播： 反向传播时，序列内所有 Token 被同等对待。

GSPO算法优化函数
J GSPO ( θ ) = E x ∼ D , { y i } i = 1 G ∼ π θ old ( ⋅ ∣ x ) 1 G ∑ i = 1 G min ⁡ [ s i ( θ ) A ^ i , clip ( s i ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ i ] J_{\text{GSPO}}(\theta) = \mathbb{E}{x \sim D, \{y_i\}{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|x)} \frac{1}{G} \sum_{i=1}^G \min \left[ s_i(\theta) \hat{A}_i, \text{clip}(s_i(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_i \right] JGSPO(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)G1i=1∑Gmin[si(θ)A^i,clip(si(θ),1−ϵ,1+ϵ)A^i]
组内相对优势 A ^ i \hat{A}i A^i（与 GRPO 相同）
A ^ i = r ( x , y i ) − mean { r ( x , y i ) } i = 1 G std { r ( x , y i ) } i = 1 G \hat{A}i = \frac{r(x, y_i) - \text{mean}\{r(x, y_i)\}{i=1}^G}{\text{std}\{r(x, y_i)\}{i=1}^G} A^i=std{r(x,yi)}i=1Gr(x,yi)−mean{r(x,yi)}i=1G
序列级重要性比 s i ( θ ) s_i(\theta) si(θ)（基于序列似然）。整段响应的分布比值（新旧策略下 y y y 的似然比），然后进行长度归一化（按 token数取几何平均）。
s i ( θ ) = ( π θ ( y i ∣ x ) π θ old ( y i ∣ x ) ) 1 / ∣ y i ∣ = exp ⁡ ( 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ log ⁡ π θ ( y i , t ∣ x , y i , < t ) π θ old ( y i , t ∣ x , y i , < t ) ) s_i(\theta) = \left( \frac{\pi_\theta(y_i|x)}{\pi_{\theta_{\text{old}}}(y_i|x)} \right)^{1/|y_i|} = \exp\left( \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \log \frac{\pi_\theta(y_{i,t}|x, y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t}|x, y_{i,<t})} \right) si(θ)=(πθold(yi∣x)πθ(yi∣x))1/∣yi∣=exp ∣yi∣1t=1∑∣yi∣logπθold(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t)

本质上是将序列级似然比转换为token级平均似然比，使不同长度序列的重要度比具有可比性。

长度归一化（length normalization） 就是对序列长度 ∣ y i ∣ |y_i| ∣yi∣进行开方，具体操作是将序列级重要性比 s i ( θ ) s_i(\theta) si(θ) 按token数取几何平均，正如上方公式。

序列级重要性比 s i ( θ ) s_i(\theta) si(θ)（基于序列似然）的设计原因。

off-policy校正：使用重要性比率修正旧策略 π θ o l d \pi_{\theta_{old}} πθold与目标策略 π θ \pi_{\theta} πθ的正态偏差。
序列级重要性比：将序列级重要比率与整段奖励单位匹配。
长度归一化
1. 数值稳定性：长序列的概率是多个小概率的乘积，会导致数值下溢
2. 消除长度偏差：不同长度的序列其原始似然比天然存在数量级差异
3. 方差控制：防止长序列因累积效应导致重要性比过大/过小
稳定裁剪：因为尺度统一，裁剪区间对不同长度的 y y y都有一致含义。

1.6 GSPO稳定性分析

GSPO算法目标（完整内容）
J GSPO ( θ ) = E x ∼ D , { y i } i = 1 G ∼ π θ old ( ⋅ ∣ x ) 1 G ∑ i = 1 G min ⁡ [ s i ( θ ) A ^ i , clip ( s i ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ i ] J_{\text{GSPO}}(\theta) = \mathbb{E}{x \sim D, \{y_i\}{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|x)} \frac{1}{G} \sum_{i=1}^G \min \left[ s_i(\theta) \hat{A}_i, \text{clip}(s_i(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_i \right] JGSPO(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)G1i=1∑Gmin[si(θ)A^i,clip(si(θ),1−ϵ,1+ϵ)A^i]
为了方便推导分析，暂时省略min函数和裁剪。
J GSPO ( θ ) = E x ∼ D , { y i } i = 1 G ∼ π θ old ( ⋅ ∣ x ) [ 1 G ∑ i = 1 G s i ( θ ) A i ] s i ( θ ) = ( π θ ( y i ∣ x ) π θ old ( y i ∣ x ) ) 1 / ∣ y i ∣ = exp ⁡ ( 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ log ⁡ π θ ( y i , t ∣ x , y i , < t ) π θ old ( y i , t ∣ x , y i , < t ) ) \begin{align*} J_{\text{GSPO}}(\theta) &= \mathbb{E}{x \sim \mathcal{D}, \{y_i\}{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G s_i(\theta) A_i \right] \\ \quad s_i(\theta) &= \left( \frac{\pi_\theta(y_i|x)}{\pi_{\theta_{\text{old}}}(y_i|x)} \right)^{1/|y_i|} = \exp\left( \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \log \frac{\pi_\theta(y_{i,t}|x, y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t}|x, y_{i,<t})} \right) \end{align*} JGSPO(θ)si(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[G1i=1∑Gsi(θ)Ai]=(πθold(yi∣x)πθ(yi∣x))1/∣yi∣=exp ∣yi∣1t=1∑∣yi∣logπθold(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t)

计算梯度简略后的GSPO目标函数：
∇ θ J GSPO ( θ ) = ∇ θ E [ ⋅ ] = E [ ∇ θ 1 G ∑ i = 1 G s i ( θ ) A i ] = E [ 1 G ∑ i = 1 G ∇ θ ( s i ( θ ) A i ) ] \nabla_\theta J_{\text{GSPO}}(\theta) = \nabla_\theta \mathbb{E}[\cdot] = \mathbb{E} \left[ \nabla_\theta \frac{1}{G} \sum_{i=1}^G s_i(\theta) A_i \right] = \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G \nabla_\theta (s_i(\theta) A_i) \right] ∇θJGSPO(θ)=∇θE[⋅]=E[∇θG1i=1∑Gsi(θ)Ai]=E[G1i=1∑G∇θ(si(θ)Ai)]
变量 θ \theta θ只依赖奖励打分与组内统计， A i A_i Ai对变量 θ \theta θ来说是常数，使用链式法则计算：
∇ θ s i ( θ ) = s i ( θ ) ∇ θ log ⁡ s i ( θ ) = E [ 1 G ∑ i = 1 G A i ∇ θ s i ( θ ) ] = E [ 1 G ∑ i = 1 G A i s i ( θ ) ∇ θ log ⁡ s i ( θ ) ] \begin{align*} \nabla_\theta s_i(\theta) &= s_i(\theta) \nabla_\theta \log s_i(\theta) \\ &= \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G A_i \nabla_\theta s_i(\theta) \right] \\ &= \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G A_i s_i(\theta) \nabla_\theta \log s_i(\theta) \right] \end{align*} ∇θsi(θ)=si(θ)∇θlogsi(θ)=E[G1i=1∑GAi∇θsi(θ)]=E[G1i=1∑GAisi(θ)∇θlogsi(θ)]
继续计算，求均值 ∇ θ log ⁡ s i ( θ ) \nabla_\theta \log s_i(\theta) ∇θlogsi(θ)

s i ( θ ) = ( π θ ( y i ∣ x ) π θ old ( y i ∣ x ) ) 1 ∣ y i ∣ s_i(\theta) = \left( \frac{\pi_\theta(y_i|x)}{\pi_{\theta_{\text{old}}}(y_i|x)} \right)^{\frac{1}{|y_i|}} si(θ)=(πθold(yi∣x)πθ(yi∣x))∣yi∣1

log ⁡ s i ( θ ) = 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ [ log ⁡ π θ ( y i , t ∣ x , y i , < t ) − log ⁡ π θ old ( y i , t ∣ x , y i , < t ) ] \log s_i(\theta) = \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \left[ \log \pi_\theta(y_{i,t} \mid x, y_{i,<t}) - \log \pi_{\theta_{\text{old}}}(y_{i,t} \mid x, y_{i,<t}) \right] logsi(θ)=∣yi∣1t=1∑∣yi∣[logπθ(yi,t∣x,yi,<t)−logπθold(yi,t∣x,yi,<t)]

旧策略项对 θ \theta θ视为常数，训练中需detach
∇ θ log ⁡ s i ( θ ) = 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ ∇ θ log ⁡ π θ ( y i , t ∣ x , y i , < t ) \nabla_\theta \log s_i(\theta) = \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \nabla_\theta \log \pi_\theta(y_{i,t} \mid x, y_{i,<t}) ∇θlogsi(θ)=∣yi∣1t=1∑∣yi∣∇θlogπθ(yi,t∣x,yi,<t)

然后将 ∇ θ log ⁡ s i ( θ ) \nabla_\theta \log s_i(\theta) ∇θlogsi(θ)带回步骤2的化简结果，同时将 s i ( θ ) s_i(\theta) si(θ)展开得到
∇ θ J GSPO ( θ ) = E [ 1 G ∑ i = 1 G s i ( θ ) A i ⋅ 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ ∇ θ log ⁡ π θ ( y i , t ∣ x , y i , < t ) ] = E [ 1 G ∑ i = 1 G ( π θ ( y i ∣ x ) π θ old ( y i ∣ x ) ) 1 ∣ y i ∣ ⋅ A i ⋅ 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ ∇ θ log ⁡ π θ ( y i , t ∣ x , y i , < t ) ] \begin{align*} \nabla_\theta J_{\text{GSPO}}(\theta) &= \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G s_i(\theta) A_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \nabla_\theta \log \pi_\theta(y_{i,t} \mid x, y_{i,<t}) \right] \\ &= \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G (\frac{\pi_\theta(y_i \mid x)}{\pi_{\theta_{\text{old}}}(y_i \mid x)})^{\frac{1}{|y_i|}} \cdot A_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \nabla_\theta \log \pi_\theta(y_{i,t} \mid x, y_{i,<t}) \right] \end{align*} ∇θJGSPO(θ)=E G1i=1∑Gsi(θ)Ai⋅∣yi∣1t=1∑∣yi∣∇θlogπθ(yi,t∣x,yi,<t) =E G1i=1∑G(πθold(yi∣x)πθ(yi∣x))∣yi∣1⋅Ai⋅∣yi∣1t=1∑∣yi∣∇θlogπθ(yi,t∣x,yi,<t)

最终公式展示三点关键内容：

类REINFORCE形态 ：标准的 ∇ log ⁡ π \nabla \log \pi ∇logπ形式，但权重在序列级（同一响应内各token等权相加）。
旧策略不回传 ： π θ o l d \pi_{\theta_{old}} πθold全程detach，只提供数值。
长度归一化 ： 1 ∣ y i ∣ \frac{1}{|y_i|} ∣yi∣1把token求和变均值，降低长度引起的方差膨胀。

对比GSPO和GRPO的梯度：

GRPO省略裁剪后的梯度为：
∇ θ J GRPO = E [ 1 G ∑ i = 1 G A i ⋅ 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ π θ ( y i , t ∣ x , y i , < t ) π θ old ( y i , t ∣ x , y i , < t ) ∇ θ log ⁡ π θ ( y i , t ∣ x , y i , < t ) ] \nabla_\theta J_{\text{GRPO}} = \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G A_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \frac{\pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t} \mid x, y_{i,<t})} \nabla_\theta \log \pi_\theta(y_{i,t} \mid x, y_{i,<t}) \right] ∇θJGRPO=E G1i=1∑GAi⋅∣yi∣1t=1∑∣yi∣πθold(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t)∇θlogπθ(yi,t∣x,yi,<t)
GRPO ：每个token的梯度前有各自的token权重 w i , t = π θ ( y i , t ∣ x , y i , < t ) π θ old ( y i , t ∣ x , y i , < t ) w_{i,t}=\frac{\pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t} \mid x, y_{i,<t})} wi,t=πθold(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t)，权重会在长序列上累积噪声，且与token层裁剪耦合，方差高、极不稳定。
GSPO ：每个序列中所有token共享一个序列级权重 s i = ( π θ ( y i ∣ x ) π θ old ( y i ∣ x ) ) 1 ∣ y i ∣ s_i=(\frac{\pi_\theta(y_i \mid x)}{\pi_{\theta_{\text{old}}}(y_i \mid x)})^{\frac{1}{|y_i|}} si=(πθold(yi∣x)πθ(yi∣x))∣yi∣1，使用相同的值聚合 ∇ log ⁡ π \nabla \log \pi ∇logπ，显著降低方差与不稳定。

将省略的梯度补充回来，继续分析
min ⁡ [ s i A i , clip ( s i , 1 − ϵ , 1 + ϵ ) A i ] \min[s_i A_i, \text{clip}(s_i, 1-\epsilon, 1+\epsilon) A_i] min[siAi,clip(si,1−ϵ,1+ϵ)Ai]

当未触发裁剪（即 s i ∈ [ 1 − ϵ , 1 + ϵ ] s_i \in [1-\epsilon, 1+\epsilon] si∈[1−ϵ,1+ϵ]）：使用用 s i A i s_i A_i siAi推导梯度，正如上面步骤4的计算结果。
当触发裁剪： ( 1 + ϵ ) A i (1+\epsilon) A_i (1+ϵ)Ai或者 ( 1 − ϵ ) A i (1-\epsilon) A_i (1−ϵ)Ai，对 s i s_i si的导数为0，因此不再通过 s i s_i si回传梯度（暂停梯度）。

裁剪让异常的off-policy样本不推动参数更新，起到信任域/步长控制的作用。GSPO在序列级裁剪，"暂停梯度"的判定更稳定；GRPO在token级裁剪，每步都可能触发/不触发，噪声门控很强。

1.7 补充：类REINFORCE形态

类REINFORCE形态指的是GSPO梯度公式呈现出与经典REINFORCE算法相同的数学结构，即 ∇ log ⁡ π \nabla \log \pi ∇logπ形式 。具体来说：
在标准REINFORCE算法中，策略梯度通常表示为：
∇ θ J = E [ ∑ t = 1 T ∇ θ log ⁡ π θ ( a t ∣ s t ) ⋅ R ] \nabla_\theta J = \mathbb{E} \left[ \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot R \right] ∇θJ=E[t=1∑T∇θlogπθ(at∣st)⋅R]
其中 R R R是整个轨迹的回报。
GSPO的梯度公式与其，虽然形式类似，但有两个关键区别：

权重在序列级 ： s i ( θ ) = π θ ( y i ∣ x ) π θ old ( y i ∣ x ) s_i(\theta) = \frac{\pi_\theta(y_i|x)}{\pi_{\theta_{\text{old}}}(y_i|x)} si(θ)=πθold(yi∣x)πθ(yi∣x)作为序列级权重
token等权相加 ：通过 1 ∣ y i ∣ \frac{1}{|y_i|} ∣yi∣1将序列内所有token的梯度等权聚合

GSPO的梯度公式本质上是一个序列级加权的REINFORCE形式 ，其中：
- ∇ θ log ⁡ π θ ( y i , t ∣ x , y i , < t ) \nabla_\theta \log \pi_\theta(y_{i,t} \mid x, y_{i,<t}) ∇θlogπθ(yi,t∣x,yi,<t)是标准的REINFORCE项
- π θ ( y i ∣ x ) π θ old ( y i ∣ x ) ⋅ A i ⋅ 1 ∣ y i ∣ \frac{\pi_\theta(y_i \mid x)}{\pi_{\theta_{\text{old}}}(y_i \mid x)} \cdot A_i \cdot \frac{1}{|y_i|} πθold(yi∣x)πθ(yi∣x)⋅Ai⋅∣yi∣1是序列级权重
这种结构保留了REINFORCE算法的核心特征，但通过序列级权重和长度归一化进行了改进。

1.8 PPO、GRPO与GSPO对比

对比维度	PPO(Proximal Policy Optimization)	GRPO (Group Relative Policy Optimization)	GSPO (Group Sequence Policy Optimization)
优化粒度	轨迹级别优化，以完整的智能体交互轨迹为单位进行策略更新	Token 级别优化	序列级别优化，与奖励计算的粒度保持一致
重要性比率计算	基于轨迹级别的概率比计算，整合单条轨迹中所有动作的概率比值，衡量新旧策略的差异	基于 token 级别的概率比计算，每个 token 独立计算重要性权重	基于序列级别的概率比计算，通过几何平均平滑处理，计算整个序列的联合概率比
专家混合模型 (MoE) 支持	原生对 MoE 支持较弱，直接应用易出现专家分配失衡问题，需结合分组、约束等改进手段	在 MoE 模型中训练不稳定，需要额外技巧来维持专家激活的一致性	天然支持 MoE 模型训练，无需额外技巧，因为只关注序列级别的似然
方差控制	通过重要性采样裁剪（Clipping）机制抑制方差，同时平衡策略更新的幅度	由于逐 token 计算重要性权重，容易引入高方差噪声	通过序列级重要性采样和长度归一化，显著降低了方差
裁剪机制	在轨迹级别对重要性比率进行裁剪，限制策略更新步长，避免过大的策略波动	在 token 级别进行裁剪，可能导致不一致的梯度更新	在序列级别进行裁剪，提供更一致和稳定的梯度更新
适用场景	适用于强化学习经典场景，如游戏博弈、机器人控制、智能体决策等，也可迁移用于部分序列生成任务	适用于对 token 级别的输出质量有高要求的任务，如细粒度文本纠错、代码逐行生成与优化	适用于以完整序列为评价单位的生成任务，如文本摘要、机器翻译、对话生成

二 GSPO-Token:GSPO的token-level变体

GSPO-token 是在标准 GSPO 基础上提出的一个变体。其核心思想是：在保持与标准 GSPO 理论梯度等价的前提下，提供对 Token 级别优势（Advantage）进行细粒度调整的灵活性。
GSPO-token目标函数：
J GSPO-token ( θ ) = E x ∼ D , { y i } i = 1 G ∼ π θ old ( ⋅ ∣ x ) 1 G ∑ i = 1 G 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ min ⁡ [ s i , t ( θ ) A i , t , clip ( s i , t ( θ ) , 1 − ϵ , 1 + ϵ ) A i , t ] J_{\text{GSPO-token}}(\theta) = \mathbb{E}{x \sim D, \{y_i\}{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|x)} \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min\left[s_{i,t}(\theta) A_{i,t}, \text{clip}(s_{i,t}(\theta), 1-\epsilon, 1+\epsilon) A_{i,t}\right] JGSPO-token(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)G1i=1∑G∣yi∣1t=1∑∣yi∣min[si,t(θ)Ai,t,clip(si,t(θ),1−ϵ,1+ϵ)Ai,t]
GSPO-token：保留 GSPO 的 min + clip 形式，但粒度处于token级别，每个 token 都有各自的重要性比 s i , t s_{i,t} si,t 和优势 A i , t A_{i,t} Ai,t。
token-level 重要性比：
s i , t ( θ ) = sg [ s i ( θ ) ] ⋅ π θ ( y i , t ∣ x , y i , < t ) sg [ π θ ( y i , t ∣ x , y i , < t ) ] s_{i,t}(\theta) = \text{sg}[s_i(\theta)] \cdot \frac{\pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\text{sg}[\pi_\theta(y_{i,t} \mid x, y_{i,<t})]} si,t(θ)=sg[si(θ)]⋅sg[πθ(yi,t∣x,yi,<t)]πθ(yi,t∣x,yi,<t)
sg [ ⋅ ] \text{sg}[\cdot] sg[⋅]: 表示 Stop Gradient（停止梯度），即将其视为常数，不参与反向传播的梯度计算。

主导部分 ( sg [ s i ( θ ) ] \text{sg}[s_i(\theta)] sg[si(θ)]) ：使用标准 GSPO 计算出的序列级重要性比 。关键的是，这个部分被Stop Gradient，所以它 不会参与梯度更新 。这意味着，整个序列的"宏观"重要性权重被固定下来了，起到了稳定器的作用，继承了 GSPO 的稳定性优势。
细调部分 ( π θ ( y i , t ∣ x , y i , < t ) sg [ π θ ( y i , t ∣ x , y i , < t ) ] \frac{\pi_{\theta}(y_{i, t} \mid x, y_{i, < t})}{\text{sg}[\pi_{\theta}(y_{i, t} \mid x, y_{i, < t})]} sg[πθ(yi,t∣x,yi,<t)]πθ(yi,t∣x,yi,<t)) ：这个部分计算了当前策略与旧策略在单个 Token 上的概率之比 。分母的 sg [ π θ ( y i , t ∣ x , y i , < t ) ] \text{sg}[\pi_{\theta}(y_{i, t} \mid x, y_{i, < t})] sg[πθ(yi,t∣x,yi,<t)] 也被 Stop Gradient 了，所以这个比率仅用于调整梯度，而不会引入额外的方差。这就好比，在宏观稳定的基础上，允许对每个 token 进行微观的、精细的调整。

特性	标准 GSPO	GSPO-token
重要性比计算层级	序列级 (Sequence-Level)	混合层级 (序列级主导 + token级调整)
梯度贡献来源	仅序列级似然比	序列级似然比 (稳定器) + Token级概率比 (精细调整)
理论梯度	稳定且可靠	与标准GSPO等价
灵活性	相对固定	更高，允许对每个 Token 的 Advantage 进行不同加权
主要应用场景	绝大多数场景，追求极致稳定性	需要更细粒度控制的场景，如多轮对话 (Multi-turn RL)

2.1 GSPO-Token梯度推导

方便推导先省略，clip和min相关结构，
∇ θ J GSPO-token = ∇ θ E [ 1 G ∑ i = 1 G 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ s i , t ( θ ) A i , t ] \nabla_\theta J_{\text{GSPO-token}} = \nabla_\theta \mathbb{E} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} s_{i,t}(\theta) A_{i,t} \right] ∇θJGSPO-token=∇θE G1i=1∑G∣yi∣1t=1∑∣yi∣si,t(θ)Ai,t
s i , t ( θ ) = sg [ s i ( θ ) ] ⋅ π θ ( y i , t ∣ x , y i , < t ) sg [ π θ ( y i , t ∣ x , y i , < t ) ] s_{i,t}(\theta) = \text{sg}[s_i(\theta)] \cdot \frac{\pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\text{sg}[\pi_\theta(y_{i,t} \mid x, y_{i,<t})]} si,t(θ)=sg[si(θ)]⋅sg[πθ(yi,t∣x,yi,<t)]πθ(yi,t∣x,yi,<t)
代入 s i , t ( θ ) s_{i,t}(\theta) si,t(θ)：
∇ θ J GSPO-token = ∇ θ E [ 1 G ∑ i = 1 G 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ ( sg [ s i ( θ ) ] ⋅ π θ ( y i , t ∣ x , y i , < t ) sg [ π θ ( y i , t ∣ x , y i , < t ) ] ) A i , t ] \nabla_\theta J_{\text{GSPO-token}} = \nabla_\theta \mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|y_i|}\sum_{t=1}^{|y_i|} \left(\text{sg}[s_i(\theta)] \cdot \frac{\pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\text{sg}[\pi_\theta(y_{i,t} \mid x, y_{i,<t})]}\right) A_{i,t}\right] ∇θJGSPO-token=∇θE G1i=1∑G∣yi∣1t=1∑∣yi∣(sg[si(θ)]⋅sg[πθ(yi,t∣x,yi,<t)]πθ(yi,t∣x,yi,<t))Ai,t
处理stop-gradient操作：由于 sg [ s i ( θ ) ] \text{sg}[s_i(\theta)] sg[si(θ)] 和 sg [ π θ ( y i , t ∣ x , y i , < t ) ] \text{sg}[\pi_\theta(y_{i,t} \mid x, y_{i,<t})] sg[πθ(yi,t∣x,yi,<t)] 都是stop-gradient操作，它们在梯度计算中被视为常数。
∇ θ J GSPO-token = E [ 1 G ∑ i = 1 G s i ( θ ) 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ A i , t ⋅ ∇ θ π θ ( y i , t ∣ x , y i , < t ) sg [ π θ ( y i , t ∣ x , y i , < t ) ] ] \nabla_\theta J_{\text{GSPO-token}} = \mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G} s_i(\theta) \frac{1}{|y_i|}\sum_{t=1}^{|y_i|} A_{i,t} \cdot \frac{\nabla_\theta \pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\text{sg}[\pi_\theta(y_{i,t} \mid x, y_{i,<t})]}\right] ∇θJGSPO-token=E G1i=1∑Gsi(θ)∣yi∣1t=1∑∣yi∣Ai,t⋅sg[πθ(yi,t∣x,yi,<t)]∇θπθ(yi,t∣x,yi,<t)
代入 s i ( θ ) s_i(\theta) si(θ)继续化简

∇ θ s i ( θ ) = s i ( θ ) ∇ θ log ⁡ s i ( θ ) \nabla_\theta s_i(\theta) = s_i(\theta) \nabla_\theta \log s_i(\theta) ∇θsi(θ)=si(θ)∇θlogsi(θ)
∇ θ log ⁡ s i ( θ ) = ∇ θ s i ( θ ) s i ( θ ) 反向写法（用于策略梯度） \nabla_\theta \log s_i(\theta) = \frac{ \nabla_\theta s_i(\theta) }{s_i(\theta)}\text{ 反向写法（用于策略梯度）} ∇θlogsi(θ)=si(θ)∇θsi(θ) 反向写法（用于策略梯度）

∇ θ J GSPO-token = E [ 1 G ∑ i = 1 G π θ ( y i ∣ x ) π θ o l d ( y i ∣ x ) 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ A i , t ∇ θ π θ ( y i , t ∣ x , y i , < t ) π θ ( y i , t ∣ x , y i , < t ) ] = E [ 1 G ∑ i = 1 G π θ ( y i ∣ x ) π θ o l d ( y i ∣ x ) A i 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ ∇ θ l o g π θ ( y i , t ∣ x , y i , < t ) ] \begin{align*} \nabla_\theta J_{\text{GSPO-token}} &= \mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G} \frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{old}}(y_i|x)} \frac{1}{|y_i|}\sum_{t=1}^{|y_i|} A_{i,t} \frac{\nabla_\theta \pi_\theta(y_{i,t} \mid x, y_{i,<t})}{\pi_\theta(y_{i,t} \mid x, y_{i,<t})}\right] \\ &= \mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G} \frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{old}}(y_i|x)} A_{i} \frac{1}{|y_i|}\sum_{t=1}^{|y_i|} \nabla_\theta log\pi_\theta(y_{i,t} \mid x, y_{i,<t}) \right] \end{align*} ∇θJGSPO-token=E G1i=1∑Gπθold(yi∣x)πθ(yi∣x)∣yi∣1t=1∑∣yi∣Ai,tπθ(yi,t∣x,yi,<t)∇θπθ(yi,t∣x,yi,<t) =E G1i=1∑Gπθold(yi∣x)πθ(yi∣x)Ai∣yi∣1t=1∑∣yi∣∇θlogπθ(yi,t∣x,yi,<t)

比较维度	GSPO	GSPO-token
优势分配	整个响应共享单一优势值A_i	每个token可独立分配优势值A_{i,t}
权重机制	序列级权重s_i	token级权重s_{i,t}（数值等于s_i）
优化粒度	序列层面	token层面
算法稳定性	较高	保持较高（继承s_i特性）
策略灵活性	相对受限	显著提升，支持细粒度局部奖励

关联：当 A i , t = A i A_{i,t}=A_i Ai,t=Ai时，与GSPO在目标函数、裁剪机制和梯度计算上完全等价。

2.2 GSPO的优势

2.2.1 GSPO在MoE训练中的优势

在MoE（混合专家）模型中，参数更新后，同一输入激活的专家网络可能发生变化(MoE的专家漂移问题)，导致GRPO等token级优化算法的权重计算出现剧烈波动，无法正常收敛。
为了解决专家漂移问题，研究者设计路由回放(Routing Replay)策略。虽然能够解决GRPO收敛问题，但是内存、通信需要额外开销，同时限制MOE模型的真实容量。

路由回放是一种训练策略，通过缓存旧策略的专家路由并在新策略中复用这些路由，确保计算重要性权重时使用相同的专家网络。

GSPO不需要路由回放，天然关注序列级 π θ ( y ∣ x ) \pi_{\theta}(y|x) πθ(y∣x)，在MOE中波动很小，整体稳定，从根本上解决MOE模型RL不收敛问题。

2.2.2 GSPO在基础设施中的优势

在实际的强化学习系统中，通常需要同时维护两类引擎，它们对精度的要求不同，导致了系统复杂度的增加：

推理引擎（如 SGLang、vLLM）：用于生成样本。侧重低延迟，通常使用混合精度，可能存在精度误差。
训练引擎（如 Megatron、DeepSpeed, FSDP）：用于反向传播与参数更新。侧重高精度，通常使用 FP16/FP32。

核心矛盾：在 GRPO 等方法中，为了进行重要性采样修正，需要在训练引擎中重新计算 token-level 的概率（ π θ o l d ( y ∣ x ) \pi_{\theta_{old}}(y|x) πθold(y∣x)），以避免推理引擎的精度误差影响权重计算。这要求基础设施必须支持复杂的"回退重算"流程，限制了训练与推理的解耦。

GSPO 通过改进算法目标，摆脱了对高精度 token-level 概率重算的依赖：

核心变化 ：GSPO 只依赖于序列级似然 （Sequence-level Likelihood）。公式表示 ：
s i ( θ ) = ( π θ ( y ∣ x ) π θ o l d ( y ∣ x ) ) 1 / ∣ y i ∣ s_i(\theta) = \left( \frac{\pi_\theta(y|x)}{\pi_{\theta_{old}}(y|x)} \right)^{1/|y_i|} si(θ)=(πθold(y∣x)πθ(y∣x))1/∣yi∣
优势：该序列级量对数值误差不敏感，因此可以直接使用推理引擎返回的似然值，无需在训练引擎中进行重新计算。

GSPO 的改进对系统工程带来了显著的正面影响：

显著简化 RL 基础设施 ：消除复杂的样本概率"再计算"流程，支持训练-推理分离架构（例如 partial rollout、多轮 RL 等场景），不再需要强耦合。
提升系统可扩展性与部署效率：降低了系统维护成本，使得模型能够更灵活地利用现有的推理集群进行扩展。

三总结

GSPO是⼀种以序列级重要性采样为核心的新型强化学习算法，它在稳定性、效率与可扩展性上超越GRPO。