大促备战中的隐蔽陷阱：Double转String会使用科学计数法展示？

一、背景：大促备战中的异常数据

大促备战期间，接到客户反馈我司上传到客户服务器上的文件存在科学计数法表示的情况（下图的4.55058496E7），与约定不符。

查看转换前的数据是：455058496，转换后（除以10：进行毫米到厘米的转换）就变成了科学计数法形式了。

问题代码：

bash 复制代码

<set var="temp.b" expr="${_item.boxLength / 10}" clazz="java.lang.String"/>

说明：

这个是个EL表达式，含义是使用expr的值作为计算逻辑，计算结果赋值给var指向的变量temp.b，类型是java.lang.String。

•_item代表当前上下文里的一个对象。

•boxLength是_item对象所具备的属性。

•该表达式先对boxLength执行除以 10 的运算，再把运算结果转换为字符串（由clazz定义的）。

业务上，boxLength是个长度的概念，单位是毫米，除以10是转换成厘米的含义。为了保证精度，系统（基于JAVA）会先将boxLength先转成java.lang.Double类型，再除以10，最后调用Double.toString()方法转成字符串。

二、问题定位：字符串转换的科学计数法陷阱

2.1 问题复现

代码：

ini 复制代码

Double depthInDouble = 455058496d/10;
log.info("depthInDouble={}", depthInDouble);

结果：

2.2 原因分析

问题就出在了最后一行，日志输出的时候Double会被转成String，调用Double.toString（）方法，而对于Double对象的值在一定的范围内，会使用科学计数法表示。

log.info的调用链（为什么会调用到Double.toStirng()）：

scss 复制代码

log.info("depthInDouble={}", depthInDouble);
  ↓
Log4jLogger.info(String format, Object arg)
  ↓
AbstractLogger.logIfEnabled(...)
  ↓
AbstractLogger.logMessage(...)
  ↓
ParameterizedMessageFactory.newMessage(...)
  ↓
ParameterizedMessage 构造函数（参数被暂存为 Object[]）
  ↓
// 此时尚未调用 Double.toString()
  ↓
// 当 Appender 执行输出时...
Appender.append(LogEvent)
  ↓
LogEvent.getMessage().getFormattedMessage() // 触发消息格式化
  ↓
ParameterizedMessage.getFormattedMessage()
  ↓
ParameterizedMessage.formatMessage(...)
  ↓
ParameterizedMessage.argToString(Object)
  ↓
Double.toString() // 终于在这里被调用！

查看Double.toString（）的源码，可以看到相关解释：

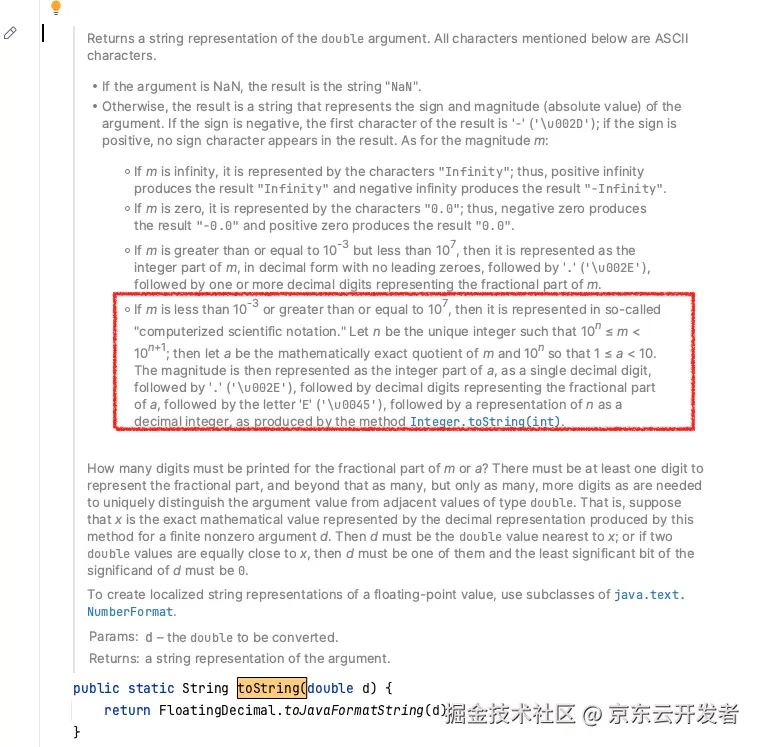
也就是说对于极小（小于10^-3）或者极大（大于10^7）值的浮点数，转成String的时候会使用科学计数法表示，验证如下。

代码：

c 复制代码

public static void main(String args[]) {
       String depth = "455058496"; // 单位：毫米
       Double depthInDouble = Double.parseDouble(depth)/10;
       String doubleInString = String.valueOf(depthInDouble);
       log.info("depthInDouble={}", depthInDouble);
       log.info("doubleInString={}", doubleInString);
       depthInDouble = 1e-3;
       log.info("10^-3 = {}", depthInDouble);
       depthInDouble = 1e7;
       log.info("10^7 = {}", depthInDouble);
       Double aVerySmallNumber = 1e-9;
       depthInDouble = 1e-3 - aVerySmallNumber;
       log.info("10^-3 - delta = {}", depthInDouble);
       depthInDouble = 1e7 - aVerySmallNumber;
       log.info("10^7 - delta = {}", depthInDouble);
   }

运行结果：

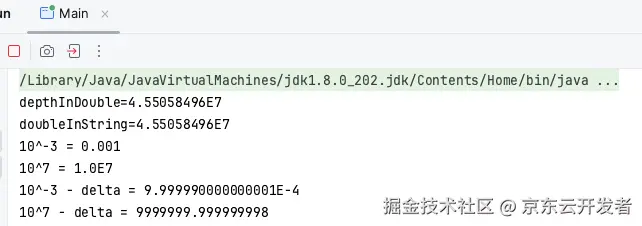
说明，10^-3不会使用科学记计数法，但是小于它就会使用科学计数法，10^7就会使用科学计数法，小于它就会不会，大于它会。

2.3 为什么要使用科学计数法

2.3.1 小数在计算机内是如何表示的

先不急于讨论为什么使用科学计数法，我们先看看小数在计算机内是如何表示的。

从存储角度来看，计算机的存储是有限资源，能存储的数据是有范围的，不是无限大，也就是说有限的硬件资源限制了计算机可以表示的数值的大小。对于一个浮点数，我们可以用10个bit存储，也可以用100个，为了实现跨设备、跨平台的数据统一表示和交换，IEEE 754 规范定义了标准格式，规定了Double类型使用64比特。

当64个比特确定了，那么它可以表示的数字的范围就确定了，接下来考虑怎么表示小数，可以表示什么范围内的小数，进而再讨论威慑么定义超过10^7或者小于10^-3使用科学计数法，而不用普通的方式（定点数表示法）。

类似整数可以利用除以2取余获得其二级制的表示形式，例如：123（10进制）= 1111011（二进制）

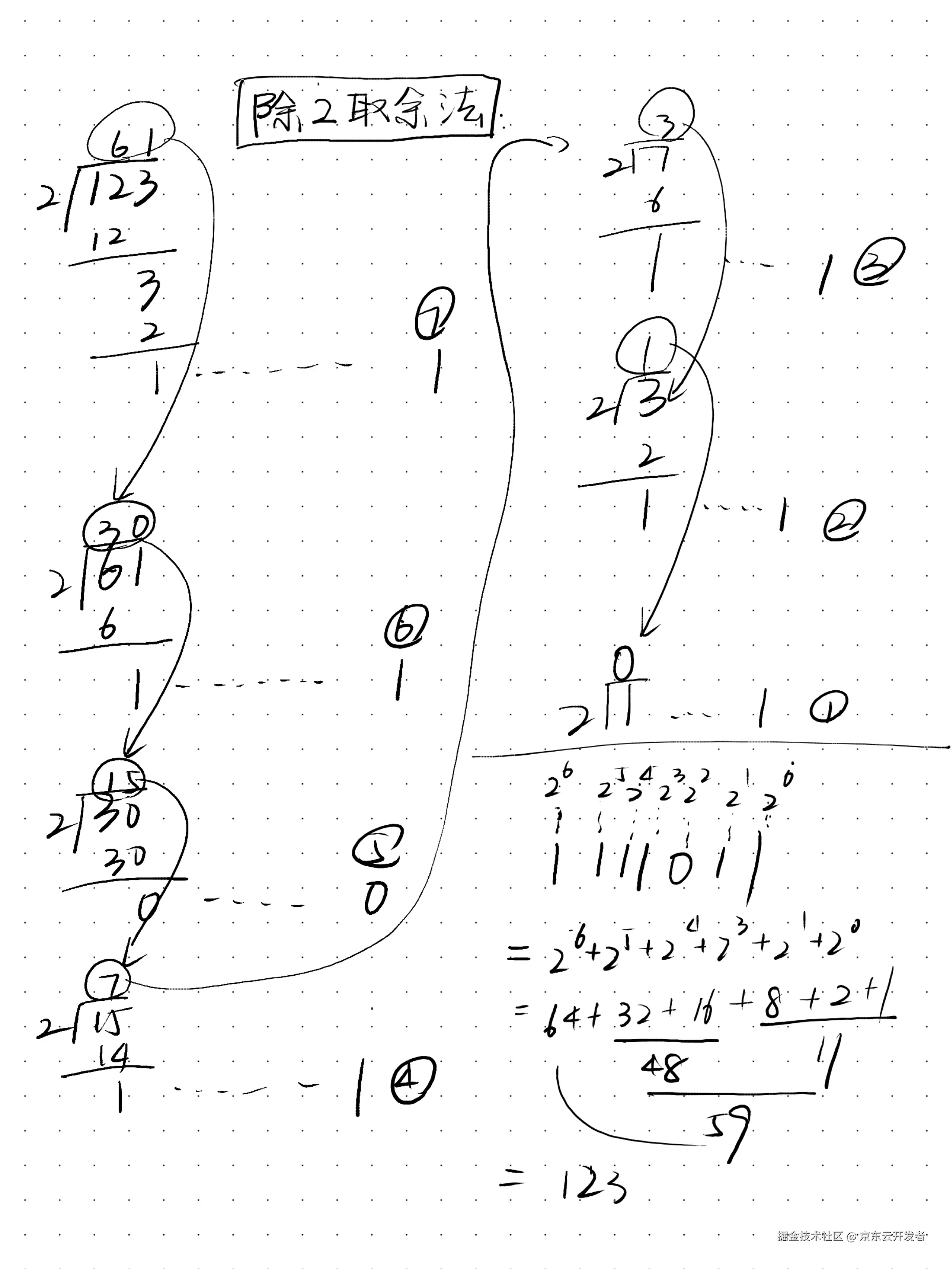
小数则进行乘2取整，如0.123（10进制）= 0. 0001111101（二进制，位数会一直循环无法精确表示，只能近似，这里取了10位）

因此最简单的一种设计（不考虑正负）就是将64位中的一部分划分为整数位，一部分划分为小数位，比如32位整数，32位小数（定点数表示法）。

那么这样设计的Double最大数可以表示2^32-1，

如果要以米为单位表示银河系直径，约1光年**≈** 299792458米/秒1年 = 299792458米/秒365天*86400秒/天 ≈ 9.45 * 10^15 ，而2^32-1≈4.29 * 10^9 （远小于1光年），因此无法使用Double表示银河系直径，无法支撑天文学科的计算了。

这样设计的Double最小可以表示2^-32=2.3810^-10 ，一个质子的大小是0.84飞米=8.410^-16，因此也无法支持物理学的计算。

所以，矛盾在于增加整数部分的位数，就会压缩小数部分的位数，不同的领域中，既有要求数字很大可表示的（在乎量级，如天文学、金融学），也有要求数值很小能表示的（在乎精度，如物理学、生物学）。

可以看到，上面的很多数字表达，我们也使用了科学计数法的表示形式来简化表达，对于上面这个数字（9.454,254,955,488,000）写起来麻烦还很占地方，而且我们也不需要那么精确，只是看个量级，因此会写成9.45 * 10^15 ，不影响理解。

即表示一个极大或者极小的数可以使用：【数值底数^指数】的形式，对于大数来讲指数就是正的，小数就是负的，计算机使用二进制，因此底数就是2，所以小数可以表示成：【数值2^指数】的形式，这个数值，其实就是尾数。

计算机专家们经过多种研究，最终经过IEEE确定了IEEE 754标准，即不确定整数和小数的位数（固定小数点，即定点数），而使用变化的位数，也就是小数点可以浮动，即浮点数表示法。浮点数表示法定义了小数由符号位+指数位+尾数位三部分组成。

符号位是1bit，0代表整数，1代表负数，指数位决定数值的量级，尾数位决定数值精度。

64位的说明如下：

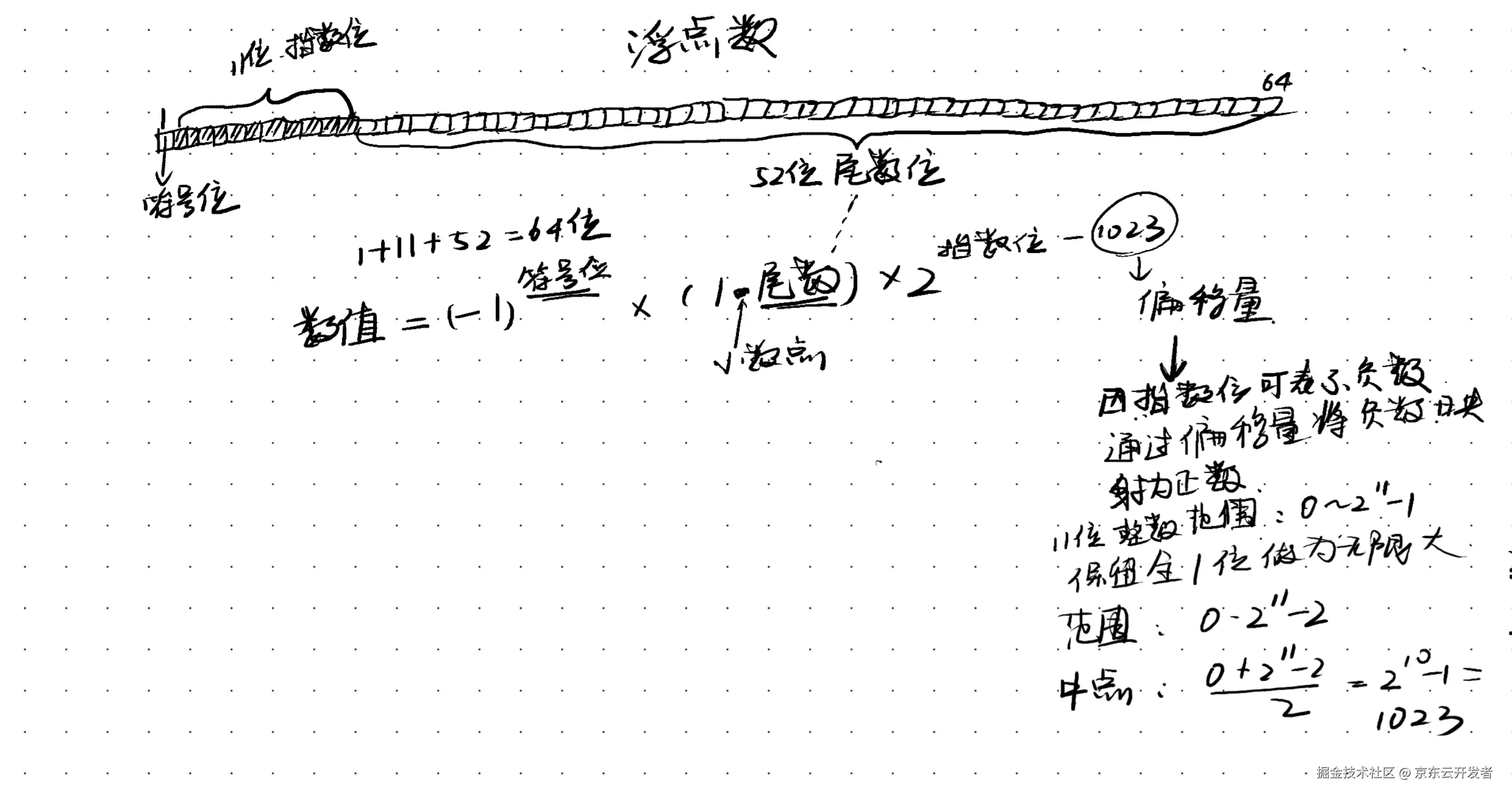
其中11和52的设计是在平衡了很多需求后得到的最佳实践。

scss 复制代码

Double (64位) = 符号位(1位) + 指数位(11位) + 尾数位(52位)

示例：455058496.0 的IEEE 754表示
原始值：455058496.0
二进制科学计数法：1.0101100001110000000000000000000 × 2^28

符号位：0 (正数)
指数位：28 + 1023(偏移量) = 1051 = 10000011011₂
尾数位：0101100001110000000000000000000... (52位)

完整64位表示：
0 10000011011 0101100001110000000000000000000000000000000000000000

2.3.2 数值超过10^7或者小于10^-3会发生什么

其实什么也不会发生，只是基于如下原因综合权衡的结果。

1、认知科学依据

•人类短期记忆的数字处理能力约为7±2位

•超过7位的整数部分难以快速理解

•科学计数法提供更好的可读性

2、精度保持考虑

•10^7 = 10,000,000 (8位数字)

•超过此值，普通格式会显得冗长

•10^-3 = 0.001，更小的数用科学计数法更清晰

3、历史兼容性

•这个标准在多种编程语言中被采用

•保持了与C语言printf的兼容性

•符合IEEE 754标准的建议

这也就是为什么这个这个范围内的数要表示成科学计数法了。

2.3.3 源码探究

1、调用链路

根据源码，可以看到Double.toString()方法的调用链是：

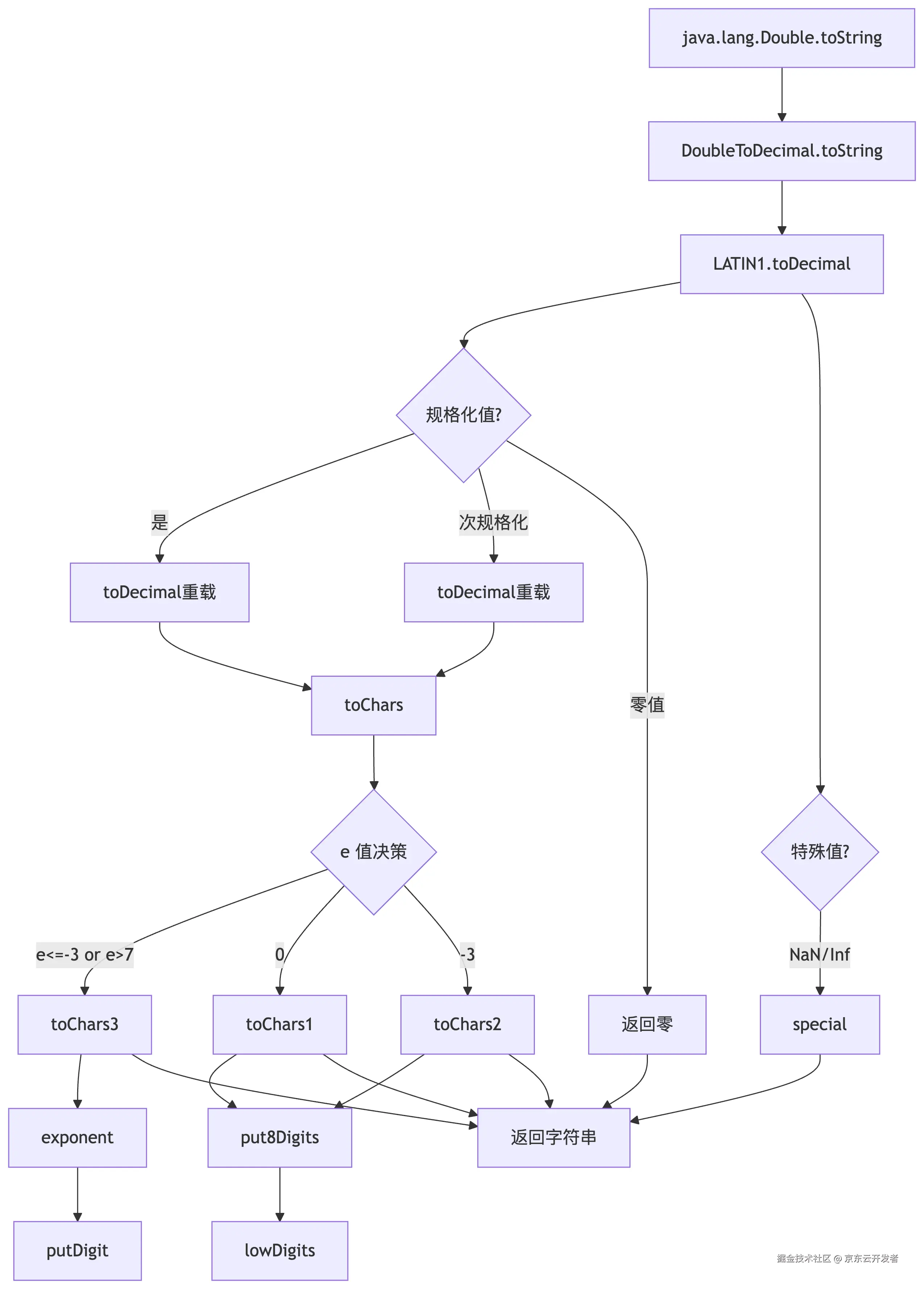
分流是否使用科学计数法的核心代码toChars的代码如下：

ini 复制代码

/*
 * Formats the decimal f 10^e.
 */
private int toChars(byte[] str, int index, long f, int e, FormattedFPDecimal fd) {
    /*
     * For details not discussed here see section 10 of [1].
     *
     * Determine len such that
     *     10^(len-1) <= f < 10^len
     */
    int len = flog10pow2(Long.SIZE - numberOfLeadingZeros(f));
    if (f >= pow10(len)) {
        len += 1;
    }
    if (fd != null) {
        fd.set(f, e, len);
        return index;
    }

    /*
     * Let fp and ep be the original f and e, respectively.
     * Transform f and e to ensure
     *     10^(H-1) <= f < 10^H
     *     fp 10^ep = f 10^(e-H) = 0.f 10^e
     */
    f *= pow10(H - len);
    e += len;

    /*
     * The toChars?() methods perform left-to-right digits extraction
     * using ints, provided that the arguments are limited to 8 digits.
     * Therefore, split the H = 17 digits of f into:
     *     h = the most significant digit of f
     *     m = the next 8 most significant digits of f
     *     l = the last 8, least significant digits of f
     *
     * For n = 17, m = 8 the table in section 10 of [1] shows
     *     floor(f / 10^8) = floor(193_428_131_138_340_668 f / 2^84) =
     *     floor(floor(193_428_131_138_340_668 f / 2^64) / 2^20)
     * and for n = 9, m = 8
     *     floor(hm / 10^8) = floor(1_441_151_881 hm / 2^57)
     */
    long hm = multiplyHigh(f, 193_428_131_138_340_668L) >>> 20;
    int l = (int) (f - 100_000_000L * hm);
    int h = (int) (hm * 1_441_151_881L >>> 57);
    int m = (int) (hm - 100_000_000 * h);

    if (0 < e && e <= 7) {
        return toChars1(str, index, h, m, l, e);
    }
    if (-3 < e && e <= 0) {
        return toChars2(str, index, h, m, l, e);
    }
    return toChars3(str, index, h, m, l, e);
}

代码地址： github.com/openjdk/jdk...

可以看到使用科学计数法处理的核心代码是toChars3，代码如下：

perl 复制代码

private int toChars3(byte[] str, int index, int h, int m, int l, int e) {
    /* -3 >= e | e > 7: computerized scientific notation */
    index = putDigit(str, index, h);
    index = putChar(str, index, '.');
    index = put8Digits(str, index, m);
    index = lowDigits(str, index, l);
    return exponent(str, index, e - 1);
}

2、toChars3()的参数含义

•byte[] str: 输出字符串的字节数组

•int index: 当前写入位置的索引

•int h: 最高位数字 (0-9)

•int m: 中间8位数字 (00000000-99999999)

•int l: 低位数字 (用于精度控制)

•int e: 调整后的十进制指数值

3、 toChars3()的数据流处理步骤

1.putDigit(str, index, h) → 写入最高位数字

2.putChar(str, index, '.') → 写入小数点

3.put8Digits(str, index, m) → 写入中间8位数字

4.lowDigits(str, index, l) → 写入低位数字（去除尾随零）

5.exponent(str, index, e-1) → 写入指数部分

为什么使用 e-1？

复制代码

原因：已经放置了一位数字在小数点前
目的：调整指数以保持数值不变
示例：4.55058496E7 表示 4.55058496 × 10^7

4、exponent()分析

css 复制代码

标准科学计数法：a.bcd × 10^n
约束条件：1 ≤ a < 10（小数点前只有一位非零数字）

perl 复制代码

private int exponent(byte[] str, int index, int exp) {
    str[index++] = (byte) 'E';  // 写入字符 'E'
    if (exp < 0) {
        str[index++] = (byte) '-';  // 负指数写入 '-'
        exp = -exp;  // 转为正数处理
    }
    if (exp >= 100) {
        str[index++] = (byte) ('0' + exp / 100);  // 百位
        exp %= 100;
    }
    if (exp >= 10) {
        str[index++] = (byte) ('0' + exp / 10);   // 十位
        exp %= 10;
    }
    str[index++] = (byte) ('0' + exp);           // 个位
    return index;
}

•输入参数 : byte[] str（输出缓冲区）、int index（写入位置）、int exp（指数值）

•核心功能: 将指数值格式化为字符串并写入字节数组

•处理逻辑: 优化处理1位、2位、3位数的指数

markdown 复制代码

1. 写入 'E'
2. 处理负号（如果 exp < 0）
3. 处理百位（如果 exp >= 100）
4. 处理十位（如果 exp >= 10）
5. 处理个位（必须）

•返回值: 更新后的索引位置

例子：

markdown 复制代码

1. 原始数值: 45505849.6
2. 精确指数: 7.658067227112319
3. 调整后指数: 7.658 - 1 = 6.658
4. 四舍五入: 7
5. exponent方法输入: exp = 7
6. 执行步骤:
   - 写入 'E' → index = 1
   - exp = 7 < 10，跳过百位和十位
   - 写入个位 '7' → index = 2
7. 输出: "E7"
8. 完整结果: "4.55058496E7"

根据源代码的逻辑简化了一版如下：

coding.jd.com/newJavaEngi...

三、解决方案

3.1 BigDecimal 精准控制

scss 复制代码

new BigDecimal(doubleValue).setScale(2, RoundingMode.HALF_UP).toPlainString()

`3.2 DecimalFormat 格式化`

scss 复制代码

new DecimalFormat("#0.00").format(doubleValue) // 强制保留两位小数

四、总结

Double 数值的字符串格式化规则（如 Double.toString()）遵循：

•普通格式（Plain）：当数值的指数范围在 [-3, 7) 时（即绝对值在 [10^-3, 10^7) 之间），直接显示小数形式（如 0.001 或 123456.0）。

•科学计数法（Scientific）：当指数范围超出 [-3, 7)（如 0.000999 或 10000000.0），显示为科学计数法（如 9.99e-4 或 1.0e7）。