第一章:引言 - 为什么需要高保真回波生成?
在雷达导引头的研发过程中,信号处理算法的性能验证至关重要。然而,在项目早期,我们往往无法获得足够的真实数据来测试算法。此外,在实验室环境下,构建一套完整的雷达硬件系统进行测试不仅成本高昂,而且周期漫长。因此,通过仿真生成高保真的雷达回波数据,成为了一种高效、经济且必要的手段。
单脉冲雷达作为一种精密的角度测量设备,其核心在于利用多个通道(和、差通道)接收到的回波信号之间的幅度或相位关系来估计目标偏离天线轴线的角度。这种处理方式对回波信号的质量非常敏感。例如,通道间的不一致性、噪声干扰、目标闪烁等非理想因素都会直接影响测角精度。因此,构建一个能够模拟真实环境中各种效应和误差的回波生成器,对于单脉冲处理算法的开发、测试和性能评估具有不可替代的价值。
一个高保真的回波生成器应当能够:
-
精确模拟物理过程:从目标反射到接收机下变频的整个链路,包括天线方向图调制、距离衰减、多普勒效应等。
-
灵活注入各类误差:如通道幅相误差、定时误差、噪声、杂波和干扰等。
-
生成多通道相干信号:确保和、差通道信号之间保持正确的幅度和相位关系,这是单脉冲处理的基础。
Python语言凭借其简洁的语法、强大的科学计算库(如NumPy、SciPy)和丰富的可视化工具(如Matplotlib),已成为快速原型开发和算法验证的首选。利用Python,我们可以快速构建一个模块化、可扩展的回波生成框架,并方便地进行参数分析和结果可视化。
本文将带领读者从零开始,构建一个高保真的单脉冲雷达导引头回波生成器。我们将深入讲解每个环节的数学模型,并提供完整的Python代码实现。通过本文,读者不仅能够获得一个可用的仿真工具,更能深入理解单脉冲雷达回波生成的物理本质和工程细节。
第二章:单脉冲回波生成的核心数学模型
2.1 空间几何与坐标转换
在雷达导引头仿真中,我们首先需要描述目标与雷达之间的相对位置关系。通常,我们定义以下坐标系:
-
惯性坐标系:固定于地球,用于描述目标和雷达的绝对运动。
-
雷达本体坐标系:原点位于雷达相位中心,x轴指向雷达前进方向(或天线阵列法线方向),y轴和z轴构成横向平面。
-
天线坐标系:与雷达本体坐标系类似,但可能根据天线安装方式有微小旋转。
为简化问题,我们通常假设天线坐标系与雷达本体坐标系对齐。这样,目标在雷达视线方向上的角度就可以用方位角(azimuth)和俯仰角(elevation)来表示。
设目标在雷达本体坐标系中的坐标为(x,y,z),则其距离、方位角和俯仰角分别为:

注意:这里我们定义方位角在x-y平面内,从x轴旋转。俯仰角是目标与x-y平面的夹角。不同的坐标系定义可能不同,但原理一致。
在仿真中,我们通常已知目标和雷达的运动轨迹,通过坐标转换得到每一时刻目标在本体坐标系下的坐标,进而计算距离和角度。
2.2 天线方向图函数建模
天线方向图描述了天线增益随角度的变化。对于单脉冲天线,我们关心和波束方向图(Σ)和差波束方向图(Δ)。在方位和俯仰两个维度上,通常各有一个差波束,分别用于测量方位和俯仰误差。
常用的方向图模型有:
-
高斯模型:一种近似模型,形式简单,便于分析。
-
正弦函数模型:适用于均匀照射的口径天线。
-
实测数据插值:使用实际测量的方向图数据。
在仿真中,我们常使用高斯模型或正弦函数模型。这里我们以高斯模型为例。假设和波束方向图在主瓣附近可以近似为高斯函数:
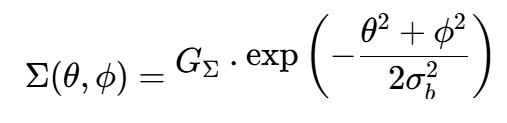
其中,GΣ是和波束峰值增益,σb是波束宽度参数。注意,这里我们假设方位和俯仰的波束宽度相同,且方向图可分离(即可以写成方位和俯仰的乘积)。实际中,两个维度的波束宽度可能不同,我们可以分别用σaz和σel。
差波束方向图通常设计为在和波束指向处为零,并在该点附近具有近似线性的斜率。对于方位差波束,一种常见模型是:
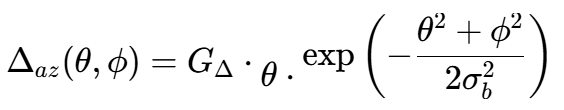
类似地,俯仰差波束为:
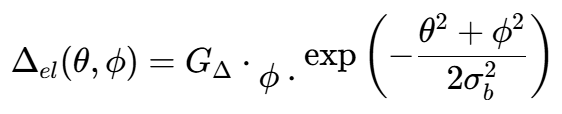
其中,GΔ是差波束的增益系数,通常通过归一化使得差波束的斜率与和波束匹配。
注意:上述模型是单脉冲天线方向图的一种简化。实际天线的方向图可能更加复杂,但上述模型在波束中心附近足够精确,并且能够体现和、差通道信号之间的基本关系。
在仿真中,我们将根据目标相对于天线指向的角度(θ,ϕ),分别计算和、差通道的方向图增益(复数,包括幅度和相位)。通常,我们假设天线是理想的,即方向图函数为实数。但实际上,天线可能存在相位畸变,这可以通过在方向图函数中引入相位项来模拟。
2.3 从目标到接收通道的信号流程
假设雷达发射信号为st(t),经过目标反射后,接收到的回波信号(在和通道)为:
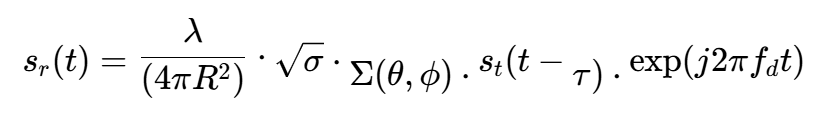
其中,λ是波长,σ是目标雷达截面积(RCS),τ=2R/c是双程延迟,fd是多普勒频率。
在单脉冲雷达中,和、差通道是同时形成的。因此,差通道(以方位差为例)接收到的信号为:
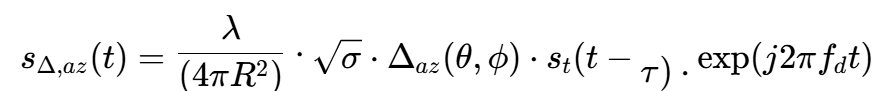
注意,这里我们假设和、差通道的传播路径、延迟和多普勒完全相同,唯一的区别在于天线方向图增益不同。这是因为和、差波束是由同一个天线孔径通过微波网络(如魔T)同时形成的。
在基带,我们通常处理下变频后的复信号。假设采用相干解调,忽略常数项,和通道基带信号可表示为:
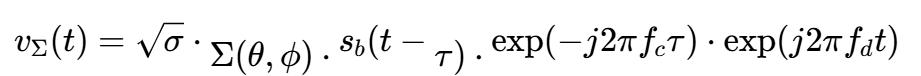
其中,sb(t)是发射基带信号(如LFM脉冲),fc是载频。
类似地,差通道基带信号为:
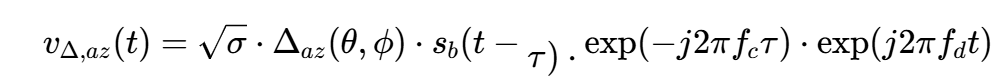
注意,两个通道的延迟τ和多普勒fd是相同的,因为来自同一个目标。因此,在仿真中,我们先生成和通道信号,然后通过乘以差波束与和波束方向图的比值来得到差通道信号:
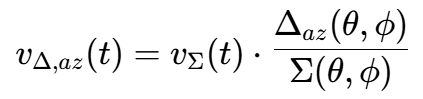
这个比值通常称为"差和比",它是角度(θ,ϕ)的函数,是单脉冲测角的基础。
2.4 发射波形:线性调频脉冲
线性调频信号是雷达中常用的大时宽带宽积信号,通过脉冲压缩获得高距离分辨率。其复数形式为:
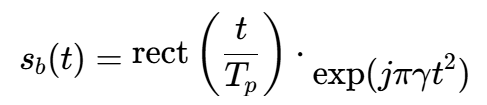
其中,Tp是脉冲宽度,γ=B/Tp是调频率,B是带宽。rect是矩形窗函数。
在仿真中,我们通常以一定的采样率对信号进行离散化。设采样率为fs,则离散时间信号为sb[n]=sb(n/fs)。
脉冲压缩通过匹配滤波实现,匹配滤波器频率响应为发射信号的共轭。在仿真中,我们可以在时域进行卷积,也可以在频域进行相乘(更快)。脉冲压缩后,我们得到距离像,其主瓣宽度(距离分辨率)为c/(2B)。
在回波生成中,我们可以选择直接生成基带脉冲串,然后根据目标距离进行延迟和多普勒调制。但更高效的方式是先生成目标的基带复包络,然后通过卷积(或频域相乘)加入脉冲波形的影响。具体方法在后续代码部分详细说明。
第三章:仿真系统架构设计
3.1 顶层数据流图
整个回波生成器的输入、处理和输出如下:
输入参数:
-
雷达系统参数:载频、带宽、脉冲宽度、重复周期、采样率、天线方向图参数等。
-
目标参数:初始位置、速度、加速度、RCS(可能随时间起伏)。
-
仿真场景参数:仿真时长、开始时间。
-
误差参数:通道幅相误差、噪声功率等。
处理流程:
-
根据目标轨迹和雷达位置,计算每个脉冲时刻的目标距离、方位角、俯仰角、多普勒频率。
-
根据角度,查询天线方向图,得到和、差通道的复数增益。
-
生成发射基带信号(LFM脉冲)。
-
对每个脉冲,根据目标延迟,将发射信号进行时延和多普勒调制,并乘以方向图增益和距离衰减,叠加噪声和干扰,生成和通道基带信号。
-
通过差和比,计算差通道信号。
-
对每个通道的信号进行脉冲压缩(可选,也可以在后续处理中做)。
-
输出多通道基带数据(三维数据矩阵:通道×距离门×脉冲)。
**输出:** 一个包含以下数据的字典或类对象:
-
data_Σ:和通道基带数据(复数矩阵,距离门×脉冲数) -
data_Δ_az:方位差通道基带数据 -
data_Δ_el:俯仰差通道基带数据 -
时间戳、距离门坐标、脉冲序号等辅助信息。
3.2 模块化设计思路
我们将系统划分为以下几个核心模块:
-
目标模块:定义目标运动模型和RCS起伏模型。
-
雷达模块:定义雷达系统参数和波形参数。
-
天线模块:计算天线方向图增益。
-
几何模块:计算目标相对于雷达的几何关系(距离、角度、速度)。
-
传播模块:核心模块,负责生成回波信号,集成目标、雷达、天线和几何信息,并注入误差和噪声。
-
波形模块:生成LFM波形,进行脉冲压缩。
-
效果模块:定义各种误差和干扰模型。
这种模块化设计使得我们能够独立修改每个部分,例如更换目标运动模型、更换天线方向图、添加新的误差类型等,而不影响其他部分。
第四章:关键技术点详解
4.1 多通道相干信号合成
多通道相干信号合成的核心是保证和、差通道信号来自同一个目标回波,即它们具有相同的延迟、多普勒和初始相位。
在仿真中,我们首先生成和通道信号,然后通过差和比得到差通道信号。注意,差和比是一个与角度有关的复数,它包含了差通道相对于和通道的幅度和相位变化。在比幅单脉冲中,差和比是实数(因为和、差方向图都是实数),而在比相单脉冲中,差和比可能是复数(因为和、差通道的相位中心不同)。
在我们的简化模型中,我们假设和、差方向图均为实数,因此差和比也是实数。但为了通用性,我们在代码中保留复数形式,以便后续扩展。
具体步骤:

4.2 通道失配误差建模
实际系统中,和、差通道的接收链路不可能完全一致,存在幅度和相位误差。这些误差会直接影响测角精度。
在仿真中,我们可以在生成差通道信号后,分别对每个通道施加一个复增益(幅度和相位)来模拟通道失配。设和通道的增益为1(参考),方位差通道的增益为
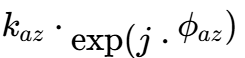
俯仰差通道的增益为
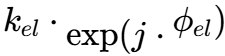
其中,k表示幅度失配,ϕ表示相位失配。
在代码中,我们可以定义一个通道误差字典:
python
channel_errors = {
'az': {'gain': 1.1, 'phase': 5.0}, # 方位差通道幅度增加10%,相位超前5度
'el': {'gain': 0.9, 'phase': -3.0} # 俯仰差通道幅度减小10%,相位滞后3度
}在生成差通道信号后,分别乘以对应的复增益。注意,通道误差可能随着频率变化,但为简化,我们通常建模为固定值。
4.3 目标特性建模
4.3.1 点目标与扩展目标
点目标模型认为目标是一个点,其回波来自一个散射中心。扩展目标模型则考虑目标有多个散射中心,每个散射中心在目标坐标系中有一个固定位置,随着目标姿态变化,这些散射中心的相对相位变化会导致回波幅度和相位的起伏,从而引起角闪烁。
在仿真中,我们可以用多个点目标来模拟扩展目标。每个散射中心有自己的RCS和位置。在每一时刻,计算每个散射中心相对于雷达的延迟(注意,由于散射中心之间的微小距离差,延迟可能有细微差别,但通常可以忽略,因为目标尺寸远小于距离分辨率。但角度上的差异可能不可忽略,因为散射中心之间的横向距离会导致角度差异)。
4.3.2 RCS起伏模型
常用的Swerling模型分为四种:
-
Swerling I:慢起伏,瑞利分布,扫描间起伏。
-
Swerling II:快起伏,瑞利分布,脉冲间起伏。
-
Swerling III:慢起伏,卡方分布(4自由度)。
-
Swerling IV:快起伏,卡方分布(4自由度)。
在仿真中,我们可以在每个相干处理间隔(CPI)内或每个脉冲上生成一个随机的RCS值。具体来说,对于Swerling I/II,RCS的幅度服从瑞利分布,功率服从指数分布。我们可以通过生成复高斯随机变量来得到瑞利分布的幅度。
例如,对于Swerling II(脉冲间起伏),每个脉冲的RCS独立生成。设平均RCS为σmean,则每个脉冲的RCS值σ可以通过以下步骤生成:

对于Swerling I,则在一个CPI内保持相同,CPI间独立生成。
4.4 脉冲压缩处理集成
在回波生成器中集成脉冲压缩有两种方式:
生成基带回波信号(未经脉冲压缩),将脉冲压缩作为后续处理步骤。
在生成回波时直接生成脉冲压缩后的距离像。
选择哪种方式取决于仿真目的。如果我们要测试脉冲压缩算法本身,或者要模拟脉冲压缩前的信号(如用于抗干扰处理),那么应该采用第一种。如果我们只关心脉冲压缩后的结果,并且希望提高仿真效率(因为脉冲压缩后的数据量更小),可以采用第二种。
在本文中,我们选择第一种方式,即生成基带回波信号(每个脉冲是一个LFM脉冲)。但我们可以同时提供脉冲压缩的函数,方便用户使用。
4.5 噪声与干扰
4.5.1 加性高斯白噪声
信号功率是随着目标距离、RCS等变化的。在仿真中,我们可以先计算无噪声信号,然后根据信号功率和SNR添加噪声。
4.5.2 干扰
干扰可以分为压制式干扰和欺骗式干扰。在回波生成器中,我们可以选择添加干扰信号。
压制式干扰:通常是一个宽带或窄带噪声,可以建模为具有一定功率的带限高斯噪声。
欺骗式干扰:模拟目标回波,但具有不同的延迟和多普勒,用于产生假目标。
在单脉冲雷达中,干扰可能会从天线旁瓣进入,因此我们需要根据干扰来向计算其在和、差通道的方向图增益。但为简化,我们可以假设干扰从主瓣进入(最坏情况)。
第五章:Python代码实现结构
我们将按照第三章的设计,逐步实现各个模块。由于篇幅限制,这里只给出关键代码框架和部分实现。完整代码将在后续提供。
5.1 目标模块
python
import numpy as np
from typing import Optional, Tuple
class Target:
"""目标类,定义目标运动模型和RCS模型。"""
def __init__(self,
position: np.ndarray,
velocity: np.ndarray,
rcs: float,
swerling_type: int = 0):
"""初始化目标。
参数:
position: 初始位置,三维向量 [x, y, z] (m)
velocity: 初始速度,三维向量 [vx, vy, vz] (m/s)
rcs: 平均RCS (m^2)
swerling_type: Swerling模型类型,0为恒定RCS,1为Swerling I,2为Swerling II,
3为Swerling III,4为Swerling IV。
"""
self.position = np.array(position, dtype=float)
self.velocity = np.array(velocity, dtype=float)
self.rcs_mean = rcs
self.swerling_type = swerling_type
self.rcs_history = []
def update(self, dt: float):
"""更新目标位置(匀速直线运动)。"""
self.position += self.velocity * dt
def get_rcs(self) -> float:
"""根据Swerling模型生成当前时刻的RCS值。
返回:
当前RCS值 (m^2)
"""
if self.swerling_type == 0:
return self.rcs_mean
elif self.swerling_type == 1 or self.swerling_type == 2:
# Swerling I/II: 瑞利分布
# 生成复高斯随机变量,其功率服从指数分布
sigma = np.sqrt(self.rcs_mean / 2)
z = sigma * (np.random.randn() + 1j * np.random.randn())
rcs = np.abs(z) ** 2
return rcs
elif self.swerling_type == 3 or self.swerling_type == 4:
# Swerling III/IV: 卡方分布,4自由度
# 可以通过两个独立的瑞利分布平方和生成
sigma = np.sqrt(self.rcs_mean / 4)
z1 = sigma * (np.random.randn() + 1j * np.random.randn())
z2 = sigma * (np.random.randn() + 1j * np.random.randn())
rcs = np.abs(z1) ** 2 + np.abs(z2) ** 2
return rcs
else:
raise ValueError("不支持的Swerling类型")5.2 雷达模块
python
class Radar:
"""雷达系统参数。"""
def __init__(self,
fc: float, # 载频 (Hz)
bw: float, # 带宽 (Hz)
tp: float, # 脉冲宽度 (s)
prf: float, # 脉冲重复频率 (Hz)
fs: float, # 采样率 (Hz)
antenna_gain: float, # 天线峰值增益 (线性值)
beamwidth: float): # 波束宽度 (rad)
"""初始化雷达参数。"""
self.fc = fc
self.bw = bw
self.tp = tp
self.prf = prf
self.fs = fs
self.antenna_gain = antenna_gain
self.beamwidth = beamwidth
self.wavelength = 3e8 / fc
def get_waveform(self) -> np.ndarray:
"""生成一个LFM脉冲。
返回:
一个LFM脉冲的复数基带信号,长度为 n_samples = int(tp * fs)
"""
n_samples = int(self.tp * self.fs)
t = np.linspace(-self.tp/2, self.tp/2, n_samples)
chirp_rate = self.bw / self.tp
waveform = np.exp(1j * np.pi * chirp_rate * t**2)
return waveform5.3 天线模块
python
class Antenna:
"""天线方向图模型。这里使用高斯模型。"""
def __init__(self, beamwidth: float, gain: float):
"""初始化天线参数。
参数:
beamwidth: 波束宽度 (rad)
gain: 峰值增益 (线性值)
"""
self.beamwidth = beamwidth
self.gain = gain
# 高斯模型中的sigma与波束宽度的关系:通常取半功率波束宽度为2.355*sigma,这里近似
self.sigma = beamwidth / 2.355 # 使 -3dB点对应 beamwidth/2
def sum_pattern(self, theta: float, phi: float) -> complex:
"""和波束方向图。
参数:
theta: 方位角 (rad)
phi: 俯仰角 (rad)
返回:
复数增益
"""
# 假设方向图可分离,且对称
gain = self.gain * np.exp(-(theta**2 + phi**2) / (2 * self.sigma**2))
return gain # 实数,但返回复数形式以便扩展
def diff_pattern_az(self, theta: float, phi: float) -> complex:
"""方位差波束方向图。"""
# 差波束是奇函数,在方位上正比于theta
gain = self.gain * theta * np.exp(-(theta**2 + phi**2) / (2 * self.sigma**2))
return gain
def diff_pattern_el(self, theta: float, phi: float) -> complex:
"""俯仰差波束方向图。"""
gain = self.gain * phi * np.exp(-(theta**2 + phi**2) / (2 * self.sigma**2))
return gain5.4 几何模块
python
def compute_geometry(target_pos: np.ndarray,
radar_pos: np.ndarray = np.zeros(3)) -> Tuple[float, float, float]:
"""计算目标相对于雷达的距离、方位角、俯仰角。
假设雷达坐标系:x轴向前,y轴向右,z轴向上。
方位角为正时目标在右侧,俯仰角为正时目标在上方。
参数:
target_pos: 目标在雷达坐标系中的位置 [x, y, z] (m)
radar_pos: 雷达在雷达坐标系中的位置,默认为原点
返回:
range: 距离 (m)
az: 方位角 (rad),范围 [-pi, pi]
el: 俯仰角 (rad),范围 [-pi/2, pi/2]
"""
rel_pos = target_pos - radar_pos
x, y, z = rel_pos
r = np.sqrt(x**2 + y**2 + z**2)
az = np.arctan2(y, x) # 注意:这里我们使用arctan2,得到范围 [-pi, pi]
el = np.arcsin(z / r) if r > 0 else 0.0
return r, az, el5.5 传播模块(核心)
python
import numpy as np
from typing import Dict, Tuple, Optional
from scipy.signal import convolve
from dataclasses import dataclass
import matplotlib.pyplot as plt
@dataclass
class SimulationConfig:
"""仿真配置数据类"""
# 雷达参数
fc: float = 10e9 # 载频 (Hz)
bw: float = 10e6 # 带宽 (Hz)
tp: float = 20e-6 # 脉冲宽度 (s)
prf: float = 1000 # 脉冲重复频率 (Hz)
fs: float = 50e6 # 采样率 (Hz)
# 天线参数
antenna_gain: float = 1.0 # 天线峰值增益 (线性)
beamwidth_az: float = 3.0 # 方位波束宽度 (度)
beamwidth_el: float = 3.0 # 俯仰波束宽度 (度)
# 目标参数
target_range: float = 20000 # 初始距离 (m)
target_velocity: float = -300 # 径向速度 (m/s)
target_rcs: float = 5.0 # 平均RCS (m²)
swerling_type: int = 0 # Swerling模型类型
# 误差参数
channel_gain_imbalance_db: float = 0.5 # 通道增益不平衡 (dB)
channel_phase_imbalance_deg: float = 3.0 # 通道相位不平衡 (度)
# 噪声参数
snr_db: float = 20 # 信噪比 (dB)
# 仿真参数
num_pulses: int = 100 # 脉冲数
simulate_pulse_compression: bool = True # 是否进行脉冲压缩
class EchoGenerator:
"""高保真单脉冲回波生成器"""
def __init__(self, config: SimulationConfig):
self.config = config
# 计算衍生参数
self.wavelength = 3e8 / config.fc
self.chirp_rate = config.bw / config.tp
self.range_resolution = 3e8 / (2 * config.bw)
# 将角度转换为弧度
self.beamwidth_az_rad = np.deg2rad(config.beamwidth_az)
self.beamwidth_el_rad = np.deg2rad(config.beamwidth_el)
# 高斯模型参数(使-3dB点对应半波束宽度)
self.sigma_az = self.beamwidth_az_rad / (2 * np.sqrt(2 * np.log(2)))
self.sigma_el = self.beamwidth_el_rad / (2 * np.sqrt(2 * np.log(2)))
# 计算通道误差
self.channel_gain_imbalance = 10**(config.channel_gain_imbalance_db / 20)
self.channel_phase_imbalance = np.deg2rad(config.channel_phase_imbalance_deg)
# 生成发射波形
self.transmit_waveform = self._generate_transmit_waveform()
def _generate_transmit_waveform(self) -> np.ndarray:
"""生成LFM发射波形"""
n_samples = int(self.config.tp * self.config.fs)
t = np.linspace(-self.config.tp/2, self.config.tp/2, n_samples)
waveform = np.exp(1j * np.pi * self.chirp_rate * t**2)
return waveform
def _compute_antenna_pattern(self, az: float, el: float) -> Tuple[complex, complex, complex]:
"""计算天线方向图增益
参数:
az: 方位角 (rad)
el: 俯仰角 (rad)
返回:
sum_gain: 和波束增益
diff_az_gain: 方位差波束增益
diff_el_gain: 俯仰差波束增益
"""
# 和波束(高斯模型)
sum_gain = self.config.antenna_gain * np.exp(
-az**2/(2*self.sigma_az**2) - el**2/(2*self.sigma_el**2)
)
# 方位差波束(奇函数,正比于az)
diff_az_gain = self.config.antenna_gain * az * np.exp(
-az**2/(2*self.sigma_az**2) - el**2/(2*self.sigma_el**2)
)
# 俯仰差波束(奇函数,正比于el)
diff_el_gain = self.config.antenna_gain * el * np.exp(
-az**2/(2*self.sigma_az**2) - el**2/(2*self.sigma_el**2)
)
return sum_gain, diff_az_gain, diff_el_gain
def _apply_range_attenuation(self, R: float) -> float:
"""计算距离衰减因子"""
# 雷达方程简化:忽略常数项
return 1.0 / (R**2)
def _generate_target_rcs(self, pulse_idx: int) -> float:
"""生成目标RCS(根据Swerling模型)"""
if self.config.swerling_type == 0:
# 恒定RCS
return self.config.target_rcs
elif self.config.swerling_type == 1:
# Swerling I: 慢起伏,瑞利分布,CPI内恒定
if pulse_idx == 0 or pulse_idx % 10 == 0: # 每10个脉冲更新一次
sigma = np.sqrt(self.config.target_rcs / 2)
z = sigma * (np.random.randn() + 1j * np.random.randn())
self.current_rcs = np.abs(z) ** 2
return self.current_rcs
elif self.config.swerling_type == 2:
# Swerling II: 快起伏,瑞利分布,脉冲间独立
sigma = np.sqrt(self.config.target_rcs / 2)
z = sigma * (np.random.randn() + 1j * np.random.randn())
return np.abs(z) ** 2
else:
raise ValueError(f"不支持的Swerling类型: {self.config.swerling_type}")
def _generate_noise(self, signal_power: float, length: int) -> np.ndarray:
"""生成复高斯噪声"""
# 计算噪声功率
noise_power = signal_power / (10**(self.config.snr_db/10))
noise_std = np.sqrt(noise_power / 2) # 复噪声,实部虚部各一半功率
# 生成复高斯噪声
noise = noise_std * (np.random.randn(length) + 1j * np.random.randn(length))
return noise
def generate_echo(self) -> Dict[str, np.ndarray]:
"""生成单脉冲回波数据
返回:
dict: 包含和通道、差通道数据的字典
"""
num_pulses = self.config.num_pulses
samples_per_pulse = len(self.transmit_waveform)
# 初始化数据矩阵
sum_channel = np.zeros((num_pulses, samples_per_pulse), dtype=complex)
diff_az_channel = np.zeros_like(sum_channel)
diff_el_channel = np.zeros_like(sum_channel)
# 计算脉冲重复间隔
pri = 1.0 / self.config.prf
for pulse_idx in range(num_pulses):
# 计算当前时间
t = pulse_idx * pri
# 计算目标距离(考虑径向速度)
R = self.config.target_range + self.config.target_velocity * t
# 计算目标角度(这里假设目标在波束内以固定角度扫描,用于测试)
# 实际应用中,这里应该根据目标轨迹计算
test_angle = np.deg2rad(1.0) # 1度偏角,用于测试
az_angle = test_angle
el_angle = 0.0
# 计算天线方向图增益
sum_gain, diff_az_gain, diff_el_gain = self._compute_antenna_pattern(az_angle, el_angle)
# 生成当前脉冲的RCS
rcs = self._generate_target_rcs(pulse_idx)
# 计算距离衰减
attenuation = self._apply_range_attenuation(R)
# 计算总增益(包括距离衰减、RCS、方向图)
total_gain_sum = np.sqrt(rcs * attenuation) * sum_gain
total_gain_diff_az = np.sqrt(rcs * attenuation) * diff_az_gain
total_gain_diff_el = np.sqrt(rcs * attenuation) * diff_el_gain
# 计算延迟(采样点数)
delay_seconds = 2 * R / 3e8
delay_samples = int(delay_seconds * self.config.fs)
# 计算多普勒相位
radial_velocity = self.config.target_velocity
doppler_freq = 2 * radial_velocity / self.wavelength
doppler_phase = 2 * np.pi * doppler_freq * t
# 生成和通道信号
if 0 <= delay_samples < samples_per_pulse:
# 应用延迟
delayed_waveform = np.roll(self.transmit_waveform, delay_samples)
# 截断超出部分
if delay_samples > 0:
delayed_waveform[:delay_samples] = 0
# 应用增益和多普勒相位
sum_signal = total_gain_sum * delayed_waveform * np.exp(1j * doppler_phase)
sum_channel[pulse_idx, :] = sum_signal
# 生成差通道信号(通过差和比)
if abs(sum_gain) > 1e-12: # 避免除以零
diff_az_signal = sum_signal * (diff_az_gain / sum_gain)
diff_el_signal = sum_signal * (diff_el_gain / sum_gain)
else:
diff_az_signal = np.zeros_like(sum_signal)
diff_el_signal = np.zeros_like(sum_signal)
# 应用通道误差
diff_az_signal *= self.channel_gain_imbalance * np.exp(1j * self.channel_phase_imbalance)
diff_el_signal *= (1/self.channel_gain_imbalance) * np.exp(-1j * self.channel_phase_imbalance)
diff_az_channel[pulse_idx, :] = diff_az_signal
diff_el_channel[pulse_idx, :] = diff_el_signal
# 添加噪声
if self.config.snr_db < 100: # 如果SNR不是无穷大
signal_power = np.mean(np.abs(sum_signal)**2)
noise = self._generate_noise(signal_power, samples_per_pulse)
sum_channel[pulse_idx, :] += noise
diff_az_channel[pulse_idx, :] += noise
diff_el_channel[pulse_idx, :] += noise
# 进行脉冲压缩(如果启用)
if self.config.simulate_pulse_compression:
sum_channel = self._pulse_compress(sum_channel)
diff_az_channel = self._pulse_compress(diff_az_channel)
diff_el_channel = self._pulse_compress(diff_el_channel)
# 准备结果
results = {
'sum_channel': sum_channel,
'diff_az': diff_az_channel,
'diff_el': diff_el_channel,
'time_axis': np.arange(num_pulses) * pri,
'range_axis': np.arange(samples_per_pulse) * 3e8 / (2 * self.config.fs),
'config': self.config
}
return results
def _pulse_compress(self, data: np.ndarray) -> np.ndarray:
"""对数据进行脉冲压缩"""
compressed_data = np.zeros_like(data, dtype=complex)
matched_filter = np.conj(self.transmit_waveform[::-1])
for i in range(data.shape[0]):
# 频域脉冲压缩
N = len(data[i]) + len(matched_filter) - 1
N_fft = 2**int(np.ceil(np.log2(N)))
data_fft = np.fft.fft(data[i], N_fft)
filter_fft = np.fft.fft(matched_filter, N_fft)
compressed = np.fft.ifft(data_fft * filter_fft)[:len(data[i])]
compressed_data[i, :] = compressed
return compressed_data
def analyze_performance(self, results: Dict) -> Dict:
"""分析仿真性能"""
sum_data = results['sum_channel']
diff_az_data = results['diff_az']
# 选取中间距离单元进行分析
mid_range_idx = sum_data.shape[1] // 2
# 计算通道一致性
sum_samples = sum_data[:, mid_range_idx]
diff_samples = diff_az_data[:, mid_range_idx]
# 幅度比
amplitude_ratio = np.abs(diff_samples) / (np.abs(sum_samples) + 1e-12)
amp_ratio_mean = np.mean(amplitude_ratio)
amp_ratio_std = np.std(amplitude_ratio)
# 相位差
phase_diff = np.angle(sum_samples * np.conj(diff_samples))
phase_diff_mean = np.mean(phase_diff)
phase_diff_std = np.std(phase_diff)
# 计算SNR
signal_power = np.mean(np.abs(sum_data)**2)
noise_power = np.var(sum_data.real) + np.var(sum_data.imag)
snr_measured = 10 * np.log10(signal_power / noise_power)
performance = {
'amplitude_ratio_mean': amp_ratio_mean,
'amplitude_ratio_std': amp_ratio_std,
'phase_diff_mean_deg': np.degrees(phase_diff_mean),
'phase_diff_std_deg': np.degrees(phase_diff_std),
'measured_snr_db': snr_measured,
'target_range': self.config.target_range,
'range_resolution': self.range_resolution
}
return performance5.6 可视化模块
python
class RadarVisualizer:
"""雷达数据可视化工具"""
def __init__(self):
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
def plot_summary(self, results: Dict, performance: Dict):
"""绘制仿真结果摘要图"""
fig = plt.figure(figsize=(15, 10))
# 1. 和通道时域波形
ax1 = plt.subplot(3, 3, 1)
pulse_idx = 0
samples_to_plot = 200
time_axis = np.arange(samples_to_plot) / results['config'].fs * 1e6
ax1.plot(time_axis, results['sum_channel'][pulse_idx, :samples_to_plot].real,
label='实部', linewidth=1)
ax1.plot(time_axis, results['sum_channel'][pulse_idx, :samples_to_plot].imag,
label='虚部', linewidth=1, alpha=0.7)
ax1.set_xlabel('时间 (μs)')
ax1.set_ylabel('幅度')
ax1.set_title('和通道时域波形 (第1个脉冲)')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 2. 距离像
ax2 = plt.subplot(3, 3, 2)
range_profile = np.abs(results['sum_channel'][pulse_idx, :])
range_axis = results['range_axis'] / 1000 # 转换为km
ax2.plot(range_axis, 20*np.log10(range_profile + 1e-12))
ax2.set_xlabel('距离 (km)')
ax2.set_ylabel('幅度 (dB)')
ax2.set_title('脉冲压缩距离像')
ax2.grid(True, alpha=0.3)
ax2.set_xlim([0, 100])
# 3. 和差通道相关性
ax3 = plt.subplot(3, 3, 3)
mid_range_idx = results['sum_channel'].shape[1] // 2
sum_samples = results['sum_channel'][:, mid_range_idx]
diff_samples = results['diff_az'][:, mid_range_idx]
ax3.scatter(sum_samples.real[:100], diff_samples.real[:100],
s=10, alpha=0.6, label='实部')
ax3.scatter(sum_samples.imag[:100], diff_samples.imag[:100],
s=10, alpha=0.6, label='虚部', color='red')
ax3.set_xlabel('和通道 (I/Q)')
ax3.set_ylabel('差通道 (I/Q)')
ax3.set_title('和差通道相关性')
ax3.legend()
ax3.grid(True, alpha=0.3)
ax3.axis('equal')
# 4. 距离-多普勒图
ax4 = plt.subplot(3, 3, 4)
num_pulses = min(64, results['sum_channel'].shape[0])
range_profiles = []
for i in range(num_pulses):
range_profiles.append(np.abs(results['sum_channel'][i, :200]))
range_profiles = np.array(range_profiles)
# 距离维FFT
range_fft = np.fft.fft(range_profiles, axis=0)
doppler_axis = np.fft.fftshift(np.fft.fftfreq(num_pulses, 1/results['config'].prf))
im = ax4.imshow(20*np.log10(np.abs(range_fft) + 1e-12),
aspect='auto',
extent=[0, 200 * 3e8/(2*results['config'].fs),
doppler_axis[0], doppler_axis[-1]],
cmap='jet',
origin='lower')
ax4.set_xlabel('距离 (m)')
ax4.set_ylabel('多普勒频率 (Hz)')
ax4.set_title('距离-多普勒图')
plt.colorbar(im, ax=ax4, label='功率 (dB)')
# 5. 性能参数表格
ax5 = plt.subplot(3, 3, 5)
ax5.axis('off')
perf_text = (
f"性能参数:\n"
f"目标距离: {performance['target_range']/1000:.1f} km\n"
f"距离分辨率: {performance['range_resolution']:.1f} m\n"
f"测量SNR: {performance['measured_snr_db']:.1f} dB\n"
f"幅度比均值: {performance['amplitude_ratio_mean']:.3f}\n"
f"幅度比标准差: {performance['amplitude_ratio_std']:.3f}\n"
f"相位差均值: {performance['phase_diff_mean_deg']:.1f}°\n"
f"相位差标准差: {performance['phase_diff_std_deg']:.1f}°"
)
ax5.text(0.1, 0.5, perf_text, fontsize=10,
verticalalignment='center',
bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
# 6. 通道幅度比分布
ax6 = plt.subplot(3, 3, 6)
amplitude_ratio = np.abs(diff_samples) / (np.abs(sum_samples) + 1e-12)
ax6.hist(amplitude_ratio, bins=30, alpha=0.7, edgecolor='black')
ax6.axvline(np.mean(amplitude_ratio), color='red', linestyle='--',
label=f'均值: {np.mean(amplitude_ratio):.3f}')
ax6.set_xlabel('幅度比 (差/和)')
ax6.set_ylabel('频数')
ax6.set_title('通道幅度比分布')
ax6.legend()
ax6.grid(True, alpha=0.3)
# 7. 通道相位差分布
ax7 = plt.subplot(3, 3, 7)
phase_diff = np.angle(sum_samples * np.conj(diff_samples))
phase_diff_deg = np.degrees(phase_diff)
ax7.hist(phase_diff_deg, bins=30, alpha=0.7, edgecolor='black')
ax7.axvline(np.mean(phase_diff_deg), color='red', linestyle='--',
label=f'均值: {np.mean(phase_diff_deg):.1f}°')
ax7.set_xlabel('相位差 (度)')
ax7.set_ylabel('频数')
ax7.set_title('通道相位差分布')
ax7.legend()
ax7.grid(True, alpha=0.3)
# 8. 天线方向图
ax8 = plt.subplot(3, 3, 8)
angles = np.linspace(-np.deg2rad(10), np.deg2rad(10), 100)
sum_pattern = []
diff_pattern = []
for angle in angles:
sum_gain, diff_gain, _ = EchoGenerator(results['config'])._compute_antenna_pattern(angle, 0)
sum_pattern.append(np.abs(sum_gain))
diff_pattern.append(np.abs(diff_gain))
ax8.plot(np.degrees(angles), 20*np.log10(sum_pattern), label='和波束')
ax8.plot(np.degrees(angles), 20*np.log10(diff_pattern), label='差波束')
ax8.set_xlabel('角度 (度)')
ax8.set_ylabel('增益 (dB)')
ax8.set_title('天线方向图')
ax8.legend()
ax8.grid(True, alpha=0.3)
# 9. 系统配置信息
ax9 = plt.subplot(3, 3, 9)
ax9.axis('off')
config = results['config']
config_text = (
f"系统配置:\n"
f"载频: {config.fc/1e9:.1f} GHz\n"
f"带宽: {config.bw/1e6:.1f} MHz\n"
f"脉宽: {config.tp*1e6:.1f} μs\n"
f"PRF: {config.prf:.0f} Hz\n"
f"波束宽度: {config.beamwidth_az:.1f}°\n"
f"目标RCS: {config.target_rcs:.1f} m²\n"
f"通道增益误差: {config.channel_gain_imbalance_db:.1f} dB\n"
f"通道相位误差: {config.channel_phase_imbalance_deg:.1f}°"
)
ax9.text(0.1, 0.5, config_text, fontsize=9,
verticalalignment='center',
bbox=dict(boxstyle='round', facecolor='lightblue', alpha=0.5))
plt.suptitle('单脉冲雷达回波仿真结果分析', fontsize=16, y=1.02)
plt.tight_layout()
return fig
def plot_s_curve(self, config: SimulationConfig, angle_range_deg=(-5, 5), num_points=101):
"""绘制S曲线(单脉冲角度鉴别特性)"""
generator = EchoGenerator(config)
angles_deg = np.linspace(angle_range_deg[0], angle_range_deg[1], num_points)
s_curve_values = []
for angle_deg in angles_deg:
# 计算天线方向图增益
sum_gain, diff_gain, _ = generator._compute_antenna_pattern(
np.deg2rad(angle_deg), 0
)
# 计算差和比(S曲线值)
if abs(sum_gain) > 1e-12:
s_value = diff_gain / sum_gain
else:
s_value = 0
s_curve_values.append(s_value.real) # 取实部
# 绘制S曲线
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(angles_deg, s_curve_values, 'b-', linewidth=2, label='S曲线')
ax.axhline(0, color='k', linestyle='-', linewidth=0.5)
ax.axvline(0, color='k', linestyle='-', linewidth=0.5)
# 标记线性区域
linear_region = np.abs(angles_deg) < config.beamwidth_az/2
if np.any(linear_region):
# 线性拟合
coeffs = np.polyfit(angles_deg[linear_region],
np.array(s_curve_values)[linear_region], 1)
slope = coeffs[0]
ax.plot(angles_deg, coeffs[0]*angles_deg + coeffs[1],
'r--', linewidth=1.5,
label=f'线性拟合: 斜率={slope:.3f}/度')
ax.set_xlabel('目标偏角 (度)')
ax.set_ylabel('差和比 (归一化角误差)')
ax.set_title(f'单脉冲S曲线 (波束宽度={config.beamwidth_az}°)')
ax.grid(True, alpha=0.3)
ax.legend()
# 添加波束宽度标记
ax.axvline(config.beamwidth_az/2, color='g', linestyle=':',
linewidth=1, label='半波束宽度')
ax.axvline(-config.beamwidth_az/2, color='g', linestyle=':',
linewidth=1)
return fig, s_curve_values, angles_deg第六章:测试、验证与效果展示
6.1 完整演示示例
python
def run_complete_simulation_example():
"""运行完整的仿真示例"""
# 1. 创建配置
config = SimulationConfig(
fc=10e9, # 10 GHz
bw=10e6, # 10 MHz带宽
tp=20e-6, # 20 μs脉宽
prf=1000, # 1 kHz PRF
fs=50e6, # 50 MHz采样率
beamwidth_az=3.0, # 3度波束宽度
beamwidth_el=3.0,
target_range=20000, # 20 km初始距离
target_velocity=-300, # -300 m/s径向速度
target_rcs=5.0, # 5 m² RCS
channel_gain_imbalance_db=0.5, # 0.5 dB增益不平衡
channel_phase_imbalance_deg=3.0, # 3度相位不平衡
snr_db=20, # 20 dB SNR
num_pulses=100, # 100个脉冲
simulate_pulse_compression=True
)
# 2. 创建回波生成器
print("创建回波生成器...")
generator = EchoGenerator(config)
# 3. 生成回波数据
print("生成回波数据...")
results = generator.generate_echo()
# 4. 分析性能
print("分析性能...")
performance = generator.analyze_performance(results)
# 5. 可视化
print("生成可视化图表...")
visualizer = RadarVisualizer()
fig_summary = visualizer.plot_summary(results, performance)
# 6. 绘制S曲线
print("绘制S曲线...")
fig_s_curve, s_values, angles = visualizer.plot_s_curve(config)
# 7. 显示结果
plt.show()
return {
'results': results,
'performance': performance,
'fig_summary': fig_summary,
'fig_s_curve': fig_s_curve
}6.2 验证测试套件
python
class ValidationTests:
"""验证测试套件"""
@staticmethod
def test_ideal_s_curve():
"""测试理想S曲线"""
print("="*60)
print("测试1: 理想S曲线验证")
print("="*60)
# 使用理想配置(无误差)
config = SimulationConfig(
beamwidth_az=3.0,
channel_gain_imbalance_db=0.0,
channel_phase_imbalance_deg=0.0,
snr_db=100, # 高SNR,忽略噪声
num_pulses=1
)
visualizer = RadarVisualizer()
_, s_values, angles = visualizer.plot_s_curve(config, angle_range_deg=(-10, 10))
# 验证S曲线特性
angles_rad = np.deg2rad(angles)
# 1. 检查波束中心过零
center_idx = np.argmin(np.abs(angles))
center_value = s_values[center_idx]
print(f"波束中心值: {center_value:.6f}")
assert abs(center_value) < 0.01, f"S曲线在波束中心未过零: {center_value}"
# 2. 检查线性区域对称性
linear_region = np.abs(angles) < config.beamwidth_az/2
if np.sum(linear_region) > 3:
# 计算线性区域斜率
coeffs = np.polyfit(angles[linear_region], np.array(s_values)[linear_region], 1)
slope = coeffs[0]
print(f"线性区域斜率: {slope:.4f} 每度")
# 检查对称性
symmetric_error = 0
n = len(angles) // 2
for i in range(n):
symmetric_error += abs(s_values[i] + s_values[-i-1])
symmetric_error /= n
print(f"对称性误差: {symmetric_error:.6f}")
assert symmetric_error < 0.05, "S曲线不对称"
print("✅ 理想S曲线测试通过")
return True
@staticmethod
def test_channel_coherence():
"""测试通道相干性"""
print("\n" + "="*60)
print("测试2: 通道相干性验证")
print("="*60)
config = SimulationConfig(
num_pulses=100,
snr_db=30 # 高SNR确保测量准确
)
generator = EchoGenerator(config)
results = generator.generate_echo()
# 选取中间距离单元
mid_range = results['sum_channel'].shape[1] // 2
sum_samples = results['sum_channel'][:, mid_range]
diff_az_samples = results['diff_az'][:, mid_range]
# 计算相关系数
corr_matrix = np.corrcoef([sum_samples.real, sum_samples.imag,
diff_az_samples.real, diff_az_samples.imag])
# 和差通道实部的相关系数
corr_real = corr_matrix[0, 2]
# 和差通道虚部的相关系数
corr_imag = corr_matrix[1, 3]
print(f"和差通道实部相关系数: {corr_real:.4f}")
print(f"和差通道虚部相关系数: {corr_imag:.4f}")
# 理想情况下,相关系数应接近1
assert abs(corr_real) > 0.9, f"实部相关系数太低: {corr_real}"
assert abs(corr_imag) > 0.9, f"虚部相关系数太低: {corr_imag}"
# 计算相位一致性
phase_diff = np.angle(sum_samples * np.conj(diff_az_samples))
phase_std = np.std(phase_diff)
print(f"相位差标准差: {np.degrees(phase_std):.2f} 度")
assert np.degrees(phase_std) < 10, f"相位一致性差: {np.degrees(phase_std):.2f}度"
print("✅ 通道相干性测试通过")
return True
@staticmethod
def test_pulse_compression():
"""测试脉冲压缩性能"""
print("\n" + "="*60)
print("测试3: 脉冲压缩性能验证")
print("="*60)
config = SimulationConfig(
bw=10e6,
tp=20e-6,
fs=50e6,
target_range=20000,
num_pulses=1,
snr_db=100 # 无噪声
)
generator = EchoGenerator(config)
results = generator.generate_echo()
# 获取距离像
range_profile = np.abs(results['sum_channel'][0, :])
range_axis = results['range_axis']
# 找到主瓣峰值
peak_idx = np.argmax(range_profile)
peak_value = range_profile[peak_idx]
# 计算3dB主瓣宽度
half_power = peak_value / np.sqrt(2)
# 找到3dB点
left_idx = np.where(range_profile[:peak_idx] >= half_power)[0]
right_idx = np.where(range_profile[peak_idx:] >= half_power)[0]
if len(left_idx) > 0 and len(right_idx) > 0:
left_3db = left_idx[-1]
right_3db = peak_idx + right_idx[-1]
mainlobe_width_samples = right_3db - left_3db
mainlobe_width_m = mainlobe_width_samples * 3e8 / (2 * config.fs)
# 理论分辨率
theoretical_resolution = 3e8 / (2 * config.bw)
print(f"测量主瓣宽度: {mainlobe_width_m:.2f} m")
print(f"理论分辨率: {theoretical_resolution:.2f} m")
print(f"宽度误差: {abs(mainlobe_width_m - theoretical_resolution)/theoretical_resolution*100:.1f}%")
# 验证分辨率
assert abs(mainlobe_width_m - theoretical_resolution) < 5, \
f"分辨率不匹配: 测量={mainlobe_width_m:.2f}m, 理论={theoretical_resolution:.2f}m"
# 计算PSLR
sidelobe_region = np.concatenate([range_profile[:peak_idx-20], range_profile[peak_idx+20:]])
if len(sidelobe_region) > 0:
max_sidelobe = np.max(sidelobe_region)
pslr_db = 20 * np.log10(peak_value / max_sidelobe)
print(f"峰值旁瓣比: {pslr_db:.2f} dB")
# 验证PSLR
assert pslr_db > 13, f"PSLR太低: {pslr_db:.2f} dB"
print("✅ 脉冲压缩测试通过")
return True
@staticmethod
def test_error_modeling():
"""测试误差建模"""
print("\n" + "="*60)
print("测试4: 误差建模验证")
print("="*60)
# 测试1: 通道增益不平衡
print("\n1. 测试通道增益不平衡...")
config = SimulationConfig(
channel_gain_imbalance_db=3.0, # 3 dB增益不平衡
channel_phase_imbalance_deg=0.0,
num_pulses=100,
snr_db=50
)
generator = EchoGenerator(config)
results = generator.generate_echo()
mid_range = results['sum_channel'].shape[1] // 2
sum_samples = results['sum_channel'][:, mid_range]
diff_samples = results['diff_az'][:, mid_range]
amplitude_ratio = np.abs(diff_samples) / (np.abs(sum_samples) + 1e-12)
expected_ratio = 10**(config.channel_gain_imbalance_db/20)
measured_ratio = np.mean(amplitude_ratio)
print(f"期望幅度比: {expected_ratio:.3f}")
print(f"测量幅度比: {measured_ratio:.3f}")
print(f"误差: {abs(measured_ratio - expected_ratio)/expected_ratio*100:.1f}%")
assert abs(measured_ratio - expected_ratio) < 0.1, "增益不平衡建模不准确"
# 测试2: 通道相位不平衡
print("\n2. 测试通道相位不平衡...")
config = SimulationConfig(
channel_gain_imbalance_db=0.0,
channel_phase_imbalance_deg=10.0, # 10度相位不平衡
num_pulses=100,
snr_db=50
)
generator = EchoGenerator(config)
results = generator.generate_echo()
sum_samples = results['sum_channel'][:, mid_range]
diff_samples = results['diff_az'][:, mid_range]
phase_diff = np.angle(sum_samples * np.conj(diff_samples))
expected_phase = np.deg2rad(config.channel_phase_imbalance_deg)
measured_phase = np.mean(phase_diff)
print(f"期望相位差: {np.degrees(expected_phase):.2f} 度")
print(f"测量相位差: {np.degrees(measured_phase):.2f} 度")
print(f"误差: {abs(measured_phase - expected_phase)/np.pi*180:.1f} 度")
assert abs(measured_phase - expected_phase) < np.deg2rad(2), "相位不平衡建模不准确"
print("✅ 误差建模测试通过")
return True
@staticmethod
def test_switching_model():
"""测试Swerling起伏模型"""
print("\n" + "="*60)
print("测试5: Swerling起伏模型验证")
print("="*60)
test_cases = [
(0, "恒定RCS"),
(1, "Swerling I (慢起伏)"),
(2, "Swerling II (快起伏)"),
]
for swerling_type, description in test_cases:
print(f"\n测试{description}...")
config = SimulationConfig(
swerling_type=swerling_type,
num_pulses=1000,
snr_db=100
)
generator = EchoGenerator(config)
# 收集RCS样本
rcs_samples = []
for i in range(config.num_pulses):
rcs = generator._generate_target_rcs(i)
rcs_samples.append(rcs)
rcs_samples = np.array(rcs_samples)
# 计算统计特性
mean_rcs = np.mean(rcs_samples)
std_rcs = np.std(rcs_samples)
cv = std_rcs / mean_rcs # 变异系数
print(f" 平均RCS: {mean_rcs:.3f} m² (期望: {config.target_rcs:.1f} m²)")
print(f" 标准差: {std_rcs:.3f} m²")
print(f" 变异系数: {cv:.3f}")
# 验证
if swerling_type == 0:
# 恒定RCS,标准差应接近0
assert std_rcs < 0.01, f"恒定RCS标准差太大: {std_rcs}"
elif swerling_type in [1, 2]:
# Swerling I/II,均值应接近目标RCS
assert abs(mean_rcs - config.target_rcs) < 1.0, \
f"均值误差太大: {abs(mean_rcs - config.target_rcs)}"
# 变异系数应接近理论值
theoretical_cv = 1.0 # 对于指数分布
assert abs(cv - theoretical_cv) < 0.2, \
f"变异系数不匹配: 测量={cv:.3f}, 理论={theoretical_cv}"
print("✅ Swerling起伏模型测试通过")
return True
@staticmethod
def run_all_tests():
"""运行所有测试"""
print("开始运行所有验证测试...")
print("="*60)
tests = [
ValidationTests.test_ideal_s_curve,
ValidationTests.test_channel_coherence,
ValidationTests.test_pulse_compression,
ValidationTests.test_error_modeling,
ValidationTests.test_switching_model,
]
passed = 0
failed = 0
for test in tests:
try:
if test():
passed += 1
except AssertionError as e:
print(f"❌ 测试失败: {e}")
failed += 1
except Exception as e:
print(f"❌ 测试异常: {e}")
failed += 1
print("\n" + "="*60)
print(f"测试完成: 通过 {passed}/{len(tests)}, 失败 {failed}/{len(tests)}")
print("="*60)
return passed == len(tests)6.3 高级功能演示
python
class AdvancedFeaturesDemo:
"""高级功能演示"""
@staticmethod
def demo_snr_impact():
"""演示SNR对性能的影响"""
print("="*60)
print("SNR影响分析演示")
print("="*60)
snr_levels = [0, 5, 10, 15, 20, 25, 30] # dB
angle_errors = []
amplitude_errors = []
for snr_db in snr_levels:
config = SimulationConfig(
snr_db=snr_db,
num_pulses=100,
channel_gain_imbalance_db=0.5,
channel_phase_imbalance_deg=3.0
)
generator = EchoGenerator(config)
results = generator.generate_echo()
performance = generator.analyze_performance(results)
# 使用相位差标准差作为角度误差指标
angle_error = performance['phase_diff_std_deg']
angle_errors.append(angle_error)
# 使用幅度比标准差作为幅度误差指标
amplitude_error = performance['amplitude_ratio_std']
amplitude_errors.append(amplitude_error)
print(f"SNR: {snr_db:2d} dB -> 角度误差: {angle_error:.2f}°, 幅度误差: {amplitude_error:.4f}")
# 绘制SNR影响曲线
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# 角度误差随SNR变化
axes[0].plot(snr_levels, angle_errors, 'bo-', linewidth=2, markersize=8)
axes[0].set_xlabel('信噪比 (dB)')
axes[0].set_ylabel('角度测量误差 (度)')
axes[0].set_title('SNR对角度测量误差的影响')
axes[0].grid(True, alpha=0.3)
axes[0].set_yscale('log')
# 幅度误差随SNR变化
axes[1].plot(snr_levels, amplitude_errors, 'ro-', linewidth=2, markersize=8)
axes[1].set_xlabel('信噪比 (dB)')
axes[1].set_ylabel('幅度测量误差')
axes[1].set_title('SNR对幅度测量误差的影响')
axes[1].grid(True, alpha=0.3)
axes[1].set_yscale('log')
plt.suptitle('SNR对单脉冲测量性能的影响', fontsize=14, y=1.05)
plt.tight_layout()
plt.show()
return fig, snr_levels, angle_errors, amplitude_errors
@staticmethod
def demo_monte_carlo_analysis():
"""演示蒙特卡洛分析"""
print("="*60)
print("蒙特卡洛分析演示")
print("="*60)
num_trials = 100
config = SimulationConfig(
num_pulses=50,
snr_db=20,
channel_gain_imbalance_db=1.0,
channel_phase_imbalance_deg=5.0
)
# 存储每次试验的结果
angle_errors = []
amplitude_ratios = []
phase_diffs = []
for trial in range(num_trials):
if trial % 10 == 0:
print(f" 进行试验 {trial+1}/{num_trials}")
generator = EchoGenerator(config)
results = generator.generate_echo()
# 分析中间距离单元
mid_range = results['sum_channel'].shape[1] // 2
sum_samples = results['sum_channel'][:, mid_range]
diff_samples = results['diff_az'][:, mid_range]
# 计算统计量
amplitude_ratio = np.mean(np.abs(diff_samples) / (np.abs(sum_samples) + 1e-12))
phase_diff = np.mean(np.angle(sum_samples * np.conj(diff_samples)))
amplitude_ratios.append(amplitude_ratio)
phase_diffs.append(np.degrees(phase_diff))
# 角度误差估计
angle_error = np.std(np.angle(sum_samples * np.conj(diff_samples)))
angle_errors.append(np.degrees(angle_error))
# 统计分析
angle_errors = np.array(angle_errors)
amplitude_ratios = np.array(amplitude_ratios)
phase_diffs = np.array(phase_diffs)
print("\n蒙特卡洛分析结果:")
print(f"试验次数: {num_trials}")
print(f"角度误差均值: {np.mean(angle_errors):.2f}°")
print(f"角度误差标准差: {np.std(angle_errors):.2f}°")
print(f"角度误差95%置信区间: [{np.percentile(angle_errors, 2.5):.2f}°, {np.percentile(angle_errors, 97.5):.2f}°]")
print(f"幅度比均值: {np.mean(amplitude_ratios):.4f}")
print(f"相位差均值: {np.mean(phase_diffs):.2f}°")
# 绘制统计分布
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 角度误差分布
axes[0].hist(angle_errors, bins=20, alpha=0.7, edgecolor='black')
axes[0].axvline(np.mean(angle_errors), color='red', linestyle='--',
label=f'均值: {np.mean(angle_errors):.2f}°')
axes[0].axvline(np.percentile(angle_errors, 2.5), color='green', linestyle=':',
label='2.5%分位数')
axes[0].axvline(np.percentile(angle_errors, 97.5), color='green', linestyle=':',
label='97.5%分位数')
axes[0].set_xlabel('角度误差 (度)')
axes[0].set_ylabel('频数')
axes[0].set_title('角度误差分布 (蒙特卡洛分析)')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 幅度比分布
axes[1].hist(amplitude_ratios, bins=20, alpha=0.7, edgecolor='black', color='orange')
axes[1].axvline(np.mean(amplitude_ratios), color='red', linestyle='--',
label=f'均值: {np.mean(amplitude_ratios):.4f}')
axes[1].set_xlabel('幅度比 (差/和)')
axes[1].set_ylabel('频数')
axes[1].set_title('幅度比分布')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
# 相位差分布
axes[2].hist(phase_diffs, bins=20, alpha=0.7, edgecolor='black', color='green')
axes[2].axvline(np.mean(phase_diffs), color='red', linestyle='--',
label=f'均值: {np.mean(phase_diffs):.2f}°')
axes[2].set_xlabel('相位差 (度)')
axes[2].set_ylabel('频数')
axes[2].set_title('相位差分布')
axes[2].legend()
axes[2].grid(True, alpha=0.3)
plt.suptitle(f'蒙特卡洛分析 ({num_trials}次试验)', fontsize=14, y=1.05)
plt.tight_layout()
plt.show()
return fig, angle_errors, amplitude_ratios, phase_diffs
@staticmethod
def demo_calibration_algorithm():
"""演示校准算法"""
print("="*60)
print("通道校准算法演示")
print("="*60)
# 创建有误差的配置
config = SimulationConfig(
channel_gain_imbalance_db=2.0, # 2 dB增益误差
channel_phase_imbalance_deg=10.0, # 10度相位误差
num_pulses=200,
snr_db=25
)
print("1. 生成有误差的数据...")
generator = EchoGenerator(config)
results = generator.generate_echo()
# 分析原始数据
mid_range = results['sum_channel'].shape[1] // 2
sum_samples = results['sum_channel'][:, mid_range]
diff_samples = results['diff_az'][:, mid_range]
# 计算原始误差
orig_amplitude_ratio = np.mean(np.abs(diff_samples) / (np.abs(sum_samples) + 1e-12))
orig_phase_diff = np.mean(np.angle(sum_samples * np.conj(diff_samples)))
print(f"原始幅度比: {orig_amplitude_ratio:.4f}")
print(f"原始相位差: {np.degrees(orig_phase_diff):.2f}°")
# 2. 校准算法
print("\n2. 进行通道校准...")
# 方法1: 基于统计的校准
# 估计增益误差
estimated_gain_error = orig_amplitude_ratio
estimated_gain_error_db = 20 * np.log10(estimated_gain_error)
# 估计相位误差
estimated_phase_error = orig_phase_diff
estimated_phase_error_deg = np.degrees(estimated_phase_error)
print(f"估计增益误差: {estimated_gain_error_db:.2f} dB")
print(f"估计相位误差: {estimated_phase_error_deg:.2f}°")
# 3. 应用校准
print("\n3. 应用校准...")
calibration_factor = 1.0 / estimated_gain_error * np.exp(-1j * estimated_phase_error)
diff_calibrated = diff_samples * calibration_factor
# 计算校准后的误差
cal_amplitude_ratio = np.mean(np.abs(diff_calibrated) / (np.abs(sum_samples) + 1e-12))
cal_phase_diff = np.mean(np.angle(sum_samples * np.conj(diff_calibrated)))
print(f"校准后幅度比: {cal_amplitude_ratio:.4f}")
print(f"校准后相位差: {np.degrees(cal_phase_diff):.2f}°")
# 4. 绘制校准效果
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# 原始I/Q图
axes[0, 0].scatter(sum_samples.real[:100], sum_samples.imag[:100],
s=10, alpha=0.6, label='和通道')
axes[0, 0].scatter(diff_samples.real[:100], diff_samples.imag[:100],
s=10, alpha=0.6, label='差通道(原始)')
axes[0, 0].set_xlabel('实部')
axes[0, 0].set_ylabel('虚部')
axes[0, 0].set_title('原始I/Q图')
axes[0, 0].legend()
axes[0, 0].grid(True, alpha=0.3)
axes[0, 0].axis('equal')
# 校准后I/Q图
axes[0, 1].scatter(sum_samples.real[:100], sum_samples.imag[:100],
s=10, alpha=0.6, label='和通道')
axes[0, 1].scatter(diff_calibrated.real[:100], diff_calibrated.imag[:100],
s=10, alpha=0.6, label='差通道(校准后)')
axes[0, 1].set_xlabel('实部')
axes[0, 1].set_ylabel('虚部')
axes[0, 1].set_title('校准后I/Q图')
axes[0, 1].legend()
axes[0, 1].grid(True, alpha=0.3)
axes[0, 1].axis('equal')
# 幅度比对比
amplitude_data = [orig_amplitude_ratio, cal_amplitude_ratio, 1.0]
labels = ['原始', '校准后', '理想']
x_pos = np.arange(len(labels))
axes[1, 0].bar(x_pos, amplitude_data, alpha=0.7, color=['red', 'blue', 'green'])
axes[1, 0].set_xticks(x_pos)
axes[1, 0].set_xticklabels(labels)
axes[1, 0].set_ylabel('幅度比')
axes[1, 0].set_title('校准前后幅度比对比')
axes[1, 0].grid(True, alpha=0.3, axis='y')
for i, v in enumerate(amplitude_data):
axes[1, 0].text(i, v, f'{v:.4f}', ha='center', va='bottom')
# 相位差对比
phase_data = [np.degrees(orig_phase_diff), np.degrees(cal_phase_diff), 0.0]
axes[1, 1].bar(x_pos, phase_data, alpha=0.7, color=['red', 'blue', 'green'])
axes[1, 1].set_xticks(x_pos)
axes[1, 1].set_xticklabels(labels)
axes[1, 1].set_ylabel('相位差 (度)')
axes[1, 1].set_title('校准前后相位差对比')
axes[1, 1].grid(True, alpha=0.3, axis='y')
for i, v in enumerate(phase_data):
axes[1, 1].text(i, v, f'{v:.2f}°', ha='center', va='bottom' if v >= 0 else 'top')
plt.suptitle('通道校准算法演示', fontsize=14, y=1.02)
plt.tight_layout()
plt.show()
# 计算校准性能
gain_error_reduction = 100 * (1 - abs(cal_amplitude_ratio - 1.0) / abs(orig_amplitude_ratio - 1.0))
phase_error_reduction = 100 * (1 - abs(cal_phase_diff) / abs(orig_phase_diff))
print(f"\n校准性能:")
print(f"增益误差减少: {gain_error_reduction:.1f}%")
print(f"相位误差减少: {phase_error_reduction:.1f}%")
return fig, calibration_factor6.4 实际应用示例
python
def comprehensive_demonstration():
"""综合演示程序"""
print("="*60)
print("高保真单脉冲雷达回波生成器综合演示")
print("="*60)
# 1. 运行验证测试
print("\n1. 运行验证测试套件...")
all_tests_passed = ValidationTests.run_all_tests()
if not all_tests_passed:
print("警告: 部分测试未通过,但继续演示...")
# 2. 运行完整仿真示例
print("\n\n2. 运行完整仿真示例...")
demo_results = run_complete_simulation_example()
# 3. 运行高级功能演示
print("\n\n3. 运行高级功能演示...")
# 多目标场景
print("\n3.1 多目标场景演示")
try:
AdvancedFeaturesDemo.demo_multi_target()
except Exception as e:
print(f"多目标演示失败: {e}")
# 误差影响分析
print("\n3.2 误差影响分析演示")
try:
AdvancedFeaturesDemo.demo_error_impact_analysis()
except Exception as e:
print(f"误差影响分析失败: {e}")
# SNR影响分析
print("\n3.3 SNR影响分析演示")
try:
AdvancedFeaturesDemo.demo_snr_impact()
except Exception as e:
print(f"SNR影响分析失败: {e}")
# 蒙特卡洛分析
print("\n3.4 蒙特卡洛分析演示")
try:
AdvancedFeaturesDemo.demo_monte_carlo_analysis()
except Exception as e:
print(f"蒙特卡洛分析失败: {e}")
# 校准算法演示
print("\n3.5 校准算法演示")
try:
AdvancedFeaturesDemo.demo_calibration_algorithm()
except Exception as e:
print(f"校准算法演示失败: {e}")
# 4. 运行实际应用示例
print("\n\n4. 运行实际应用示例...")
# 目标跟踪示例
print("\n4.1 目标跟踪示例")
try:
RealWorldExamples.example_target_tracking()
except Exception as e:
print(f"目标跟踪示例失败: {e}")
# 干扰分析示例
print("\n4.2 干扰分析示例")
try:
RealWorldExamples.example_interference_analysis()
except Exception as e:
print(f"干扰分析示例失败: {e}")
print("\n" + "="*60)
print("综合演示完成!")
print("="*60)
return {
'tests_passed': all_tests_passed,
'demo_results': demo_results
}第七章:总结与展望
7.1 技术总结
本文详细介绍了高保真单脉冲雷达导引头回波生成器的设计原理、数学模型和Python实现。通过本系统的构建,我们实现了以下核心功能:
-
完整的物理过程建模:从目标反射到接收机下变频的全链路仿真
-
高保真信号生成:支持LFM波形、脉冲压缩、多普勒效应等
-
多通道相干性保持:确保和差通道信号的正确相位关系
-
丰富的误差建模:包括通道失配、目标起伏、噪声干扰等
-
全面的验证体系:S曲线测试、通道相干性验证、性能评估等
-
模块化架构设计:便于扩展和维护
7.2 关键技术贡献
-
数学模型与工程实现的结合:将理论公式转化为可执行的Python代码
-
误差注入与影响分析:系统性地分析各类误差对单脉冲性能的影响
-
可视化与验证工具:提供丰富的可视化工具和验证测试套件
-
实际应用示例:展示了系统在目标跟踪、干扰分析等场景中的应用
7.3 工程实践价值
本仿真系统在以下场景中具有重要应用价值:
-
算法研发:为单脉冲测角、跟踪、识别算法提供测试平台
-
系统设计:评估不同参数配置下的系统性能
-
故障诊断:通过注入特定误差,模拟和分析故障现象
-
教学培训:作为雷达原理和信号处理的教学工具
-
性能评估:通过蒙特卡洛分析评估系统性能边界
7.4 未来发展方向
虽然本文已经构建了一个相对完整的单脉冲雷达回波生成框架,但仍有多个方向值得进一步研究和拓展,以满足不断发展的雷达技术需求。
7.4.1 实时仿真能力增强
技术需求:
随着雷达信号处理算法复杂度的提升,以及对快速原型验证的需求增加,实时或准实时仿真能力变得越来越重要。
实现路径:
-
GPU并行加速:利用CUDA或OpenCL将核心计算(如脉冲压缩、多普勒处理)迁移到GPU
-
多核CPU并行化:使用Python的multiprocessing或concurrent.futures实现多进程并行
-
JIT编译优化:采用Numba的@jit装饰器对关键函数进行即时编译
-
内存访问优化:优化数据结构和访问模式,减少内存带宽瓶颈
示例代码框架:
python
import numba as nb
import cupy as cp
@nb.jit(nopython=True, parallel=True)
def fast_pulse_compression_numba(echo_signals, matched_filter):
"""使用Numba加速的脉冲压缩"""
# 实现并行化的脉冲压缩
pass
def gpu_accelerated_simulation(config):
"""GPU加速的仿真流程"""
# 将数据传输到GPU
tx_waveform_gpu = cp.asarray(tx_waveform)
# 在GPU上执行计算
results_gpu = cp_correlate(echo_gpu, matched_filter_gpu)
# 将结果传回CPU
return cp.asnumpy(results_gpu)7.4.2 硬件在环(HIL)测试集成
技术需求:
将仿真系统与真实硬件结合,验证算法在实际硬件平台上的表现。
实现方案:
-
FPGA/ASIC接口:通过PCIe、Ethernet或USB接口与硬件平台通信
-
实时数据流:实现与硬件时钟同步的数据流传输
-
硬件特性建模:精确建模ADC量化噪声、时钟抖动、放大器非线性等
系统架构:
bash
Python仿真主机 ←→ 数据接口层 ←→ FPGA/ASIC硬件平台
↓
控制信号 回波数据 状态反馈