这是学习笔记,方便自己复习,其他同学 也可以找到这个课程。
这是leetcode 的官方算法课程,售价399,说实话有点小贵,但是只要坚持学完,肯定是稳赚不亏。
一共需要花147小时 也就是 每天3h 的学习强度。根据刻意练习原理,时间一定要给够,如果每天3h不够 你就花4h,多花时间 精力 集中注意力,挑战自己,才能变得更优秀。
第一天的学习内容很简单,预备学习。
课程介绍 学习安排:
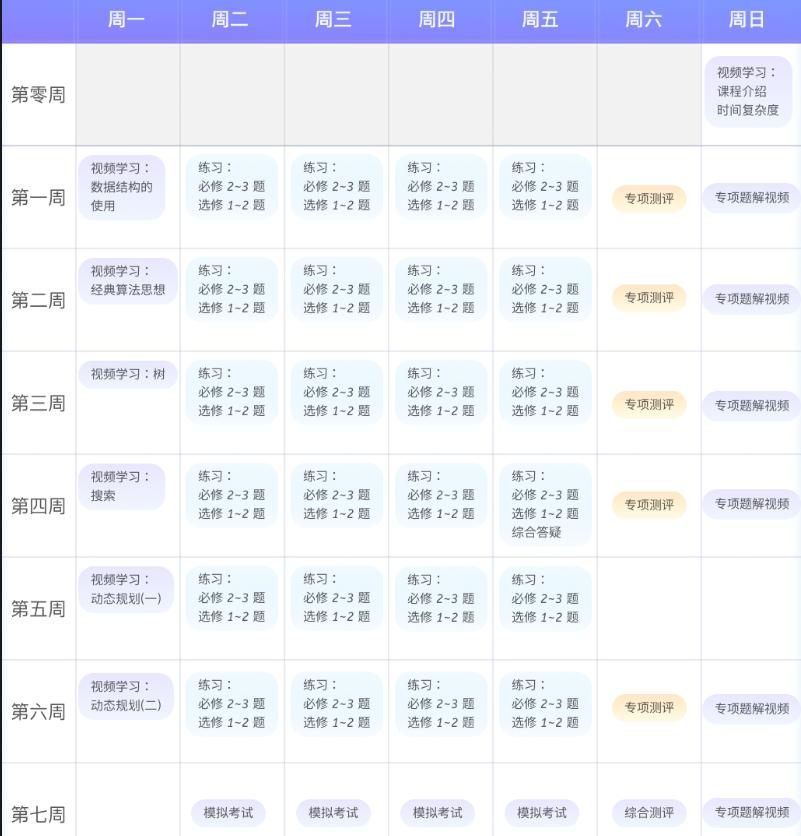
其实需要50天的 算法学习,因为第一天也算一天。
教程老师的个人信息

答疑服务
视频有解答,多看学习讨论区。
专项评测
每周一次,除了动态规划 两周才一次。
考试 是 在有压力的情况下 练习编码。
每天刷题 多少??
必修题 + 选修题
每天三道题。
学习安排

难度设置
主要争对 面试 而不是 算法竞赛。
算法复杂度
时间复杂度 + 空间复杂度
如果没有特别说明 复杂度都是指时间复杂度。
教程里使用的是 python的语法。
估算计算次数

这里一共计算了 n次

这里计算了n*n 次

这个例子中
第一次循环 经历了 n 次
第二次循环 经历了n-1 次
。。。
第n次循环 经历了 1次
等差数列求和
一共计算 (n+1)*n / 2 次
用计算次数 代表时间复杂度
前面加一个 o()

为了方便 我们一般只保留 最高次的项
也就是 (n^2) / 2
并且不保留系数
时间复杂度 就是 o(n^2)
为什么 不保留系数?

我们可以明显 感觉到 第二次 要比第一次 多10倍的计算次数
但是

当n 很大时 这个10倍就 不太重要了。
这和 物理的数量级 有类似 但是 也有差别。
当数据量小时 时间复杂度高的 也可能更慢

加入n 只有2
前面 的次数是 40 后面 却是 8
复杂度低的代码 运行时间反而更长了。
leetcode 给出的运行时间,只做参考,不具备绝对的指导意义!!!
重点关注算法的时间复杂度
例题1: 指数时间复杂度
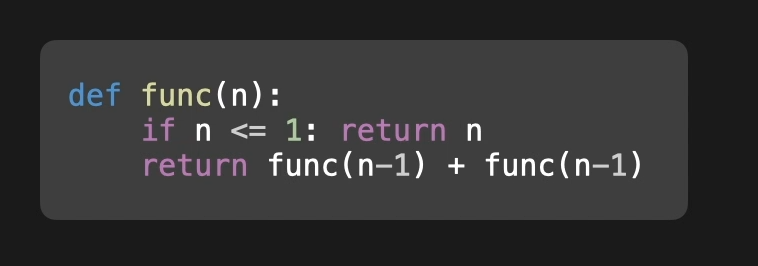
这是一个递归函数
当n 大于1时候
不进入 if 继续调用函数 参数变为n-1
例如n = 2
func(2){
return func(1){ return 1 } + func(1){return 1}
}
要计算 1次func(n)
就要计算 2次 func(n-1)
4次func(n-2)
8次func(n-3)
.。。。
2^(n-1) 次 func (n-(n-1))
一共调用了 2^n 次 func 函数
时间复杂度为 o(2^n)
例题2: 对数时间复杂度
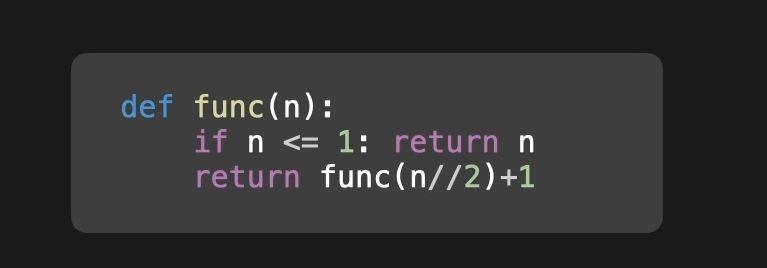
地板除

当n 等于1 时 直接调用一次
当n 等于2时 调用2次
当n 等于3时 2次
当n 等于4时 3次
。。。
当n等于 2^x 时 x+1 次
一共计算 log2(n)+ 1 次
时间复杂度为 o(log2(n))
例题3 渐进复杂度
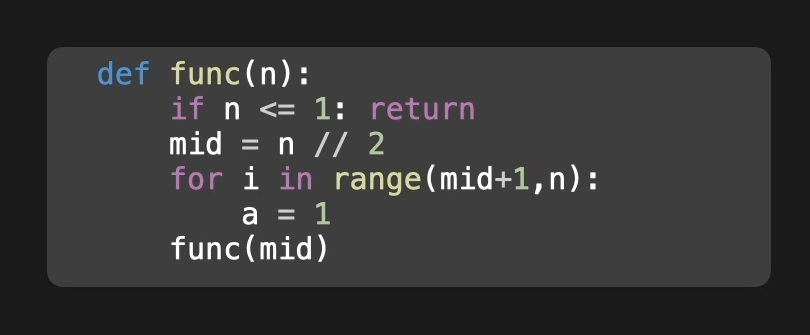
n=1 调用一次
n=2 1+
这个方法好像 有点恼火了。
f(n) = f(n/2) + n/2
计算次数:
n/2 + n/4 + n/8 + 。。。
结果为n
时间复杂度 就是 o(n)
例题4 均摊复杂度

单次操作:
当x == 0 时
只执行一次 时间复杂度为o(1)
当x!= 0 时
执行 min(a.size ,x) 次
最坏的情况 就是x比a.size大 执行a.size次 假设a的容量为n
时间复杂度为 o(n)
n次操作:
x == 0
时间复杂度 o(n)
x!=0
时间复杂度 o(n^2)
总体复杂度:
假设我们一共执行了n次 func(x)
其中 k 次 x==0 ,运行1次 push添加了 k个元素
其中 n-k 次 x!=0 ,按道理可以运行 n-k次,但是由于只有添加了k个元素 所以只能运行k次。
总共操作次数为 ( k+ (最多k次) )<= 2k
其中 k 和 n 是线性关系 成正比 假设系数为a (a<1)
所以最多执行 2* a *n 次
忽略系数之后 时间复杂度为 o(n)