Improved algorithm for the deinterleaving of radar pulses
D.J. Milojevic B.M. Popovic
Indexing terms: Algorithms, Radar and radio navigation, Signal processing
(索引词:算法、雷达与无线电导航、信号处理)
摘要
本文提出了一种改进的雷达信号解交织方法,该方法基于到达时间分析,并利用序贯差分直方图(SDIF)确定脉冲重复间隔(PRI)。推导了SDIF直方图中的最优检测阈值,这极大地提升了算法的效率。该算法适用于传统雷达、捷变频雷达和参差PRI雷达信号。结果表明,新方法在高脉冲密度雷达环境和复杂信号类型下表现优异。本文还重点探讨了该方法在多参数解交织算法中的应用。
1 引言
雷达脉冲解交织作为雷达侦察系统的重要组成部分,是检测和识别不同同时工作的雷达辐射源的过程。其核心是根据接收脉冲的特定辐射源属性对脉冲进行分类。
解交织算法基于对接收雷达脉冲各类参数的分析,例如到达时间(TOA)、到达角(AOA)、脉冲幅度、脉冲宽度和载波频率。本文提出的解交织算法属于所谓的"仅基于间隔"类算法,仅利用到达时间(TOA)信息进行解交织。
该算法的原始版本[1]基于TOA脉冲的累积差分(CDIF)直方图,下文将进行描述。本文所述为该算法的改进版本,基于新的序贯差分直方图(SDIF)技术。
2 基本算法描述
基本算法[1]依赖于CDIF直方图分析。CDIF直方图通过TOA差值构建:相邻脉冲(间隔为1)之间计算得到的TOA差值称为一阶差分;每个脉冲与间隔一个脉冲的下一个脉冲(间隔为2)之间的TOA差值称为二阶差分,依此类推。CDIF直方图会对每个差异等级的直方图数值进行累积,脉冲重复间隔(PRI)的潜在值对应于直方图的峰值。
对于每个c级TOA差值,构建CDIF直方图并定义新的阈值(阈值的选择将在后续讨论)。将每个直方图数值及其两倍值与阈值进行比较,若这些数值对均未超过阈值,则计算下一个c+1级TOA差值并构建新的累积直方图。
若识别出潜在PRI,算法将执行序列搜索[1],即寻找一组形成周期性脉冲序列的脉冲,其周期等于PRI。此类脉冲组被称为PRI序列。若搜索成功,将从输入缓冲区中提取该PRI序列,并重新构建CDIF直方图(从一阶差分开始)。只要输入缓冲区中存在足够脉冲可形成任意PRI序列,此过程就会重复进行。若未检测到PRI序列(即脉冲无法形成PRI序列),则计算下一个差值;若所有直方图数值均未超过阈值,同样计算下一个差值;若多个直方图数值超过阈值,则从最小的潜在PRI值开始,对每个潜在PRI值执行序列搜索。
参考文献[1]中提出的技术相比传统已发表技术(如由所有TOA差值构建的ΔT直方图[2]、τ直方图[2]),对干扰和脉冲缺失的敏感性更低。
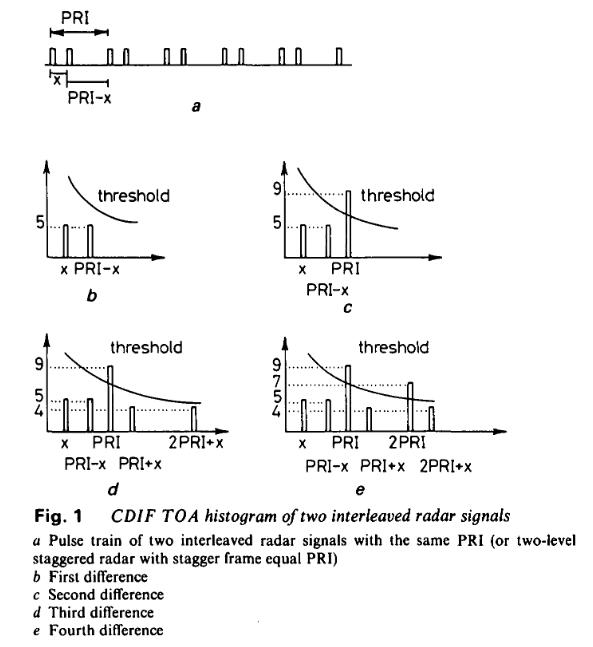
图1展示了某信号的四个连续CDIF到达时间直方图,该信号既可以表示两个交错的、具有相同PRI的稳定脉冲序列,也可以表示参差帧速率等于PRI的两级参差信号。通过该算法,N级参差信号将被识别为N个具有恒定PRI(等于参差帧速率)的信号[1]。要提取真实PRI值,需将差异等级提高至4级。
在我们看来,原始算法最显著的缺陷在于,即使在图1所示的简单情况下,也需要大量差异等级。由于要求存在二次谐波,PRI计算仅限于出现三个事件序列的情况,而非仅需两个事件的情况。然而,在算法的第二部分(序列搜索)中,通过采用适当的PRI序列检测和提取条件,可实现相同效果。因此,若摒弃二次谐波必须存在的条件,则差异直方图中的累积过程不再必要。这是我们采用序贯差分直方图(不在连续差异等级中进行累积)的主要原因。
3 改进算法描述
新算法总体分为两部分,即PRI估计和序列搜索。PRI估计作为解交织算法的核心部分,将在后续详细描述;序列搜索也是算法的重要组成部分,可显著提升算法的速度、可靠性和效率。然而,新算法中使用的序列搜索与参考文献[1]中的一致,主要目的是为了公平对比原始算法与改进后的新算法。

图2为图1中两个交错的相同PRI雷达信号的SDIF直方图。SDIF直方图中仅包含当前差值,因此相比对应的CDIF直方图更加清晰。要提取真实PRI,仅需计算二阶差分并将直方图数值与阈值进行比较,无需将两倍PRI与阈值对比,因此计算时间减少一半以上。
通过以下改进,可消除或减轻基本算法的其他缺陷:
(i)计算一阶差分时,若仅有一个直方图数值超过阈值,则该数值即为待执行序列搜索的潜在PRI。但在存在多个辐射源的情况下,一阶差分直方图可能会出现多个超过阈值的数值,且均不对应真实PRI值。因此,必须在不进行前期序列搜索的情况下计算下一个差值(参考文献[1]中提出的基本算法未考虑此步骤)。图3展示了在三个交错雷达信号(两个传统雷达,PRI分别为217μs和248μs;一个参差雷达,参差帧速率为318μs)的情况下,需要跳过一阶差分的场景。SDIF直方图的一阶差分未呈现真实PRI值,因为这些值隐藏在更高阶差分中。

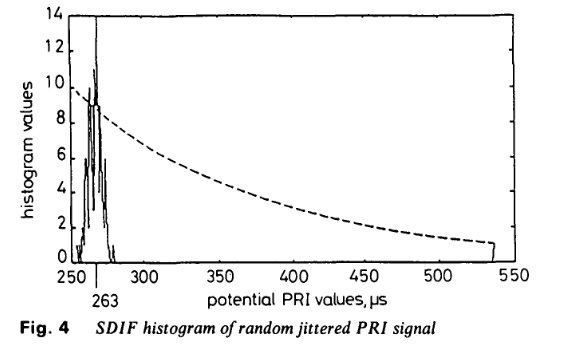
(ii)实际场景中,由于发射机电路的非理想特性,PRI值总会存在随机抖动。因此,SDIF直方图中围绕真实PRI值聚类的相似PRI值可能会产生超过阈值的直方图数值。若PRI值的范围不超过允许公差,则对代表潜在抖动PRI的中心值执行序列搜索。图4对此进行了说明:超过阈值的直方图数值对应一个检测到的辐射源,其随机抖动PRI的中心值为263μs。
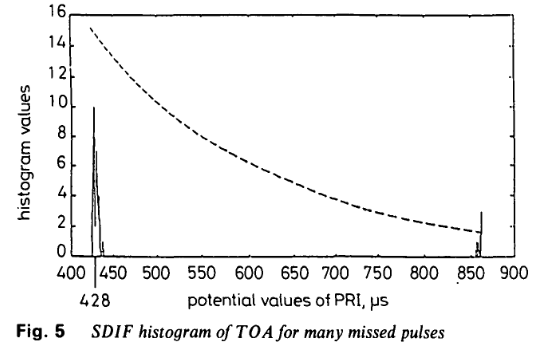
(iii)当大量脉冲缺失时,基本PRI的谐波可能在SDIF直方图中产生显著分量,这些值可能占据主导地位并超过阈值。若对应真实PRI值的直方图数值也超过阈值,则不会产生问题,因为PRI分析和序列搜索将从直方图数值超过阈值的最小PRI开始;但如果真实PRI未超过阈值,则其谐波将用于序列搜索,可能导致提取错误的PRI序列。图5为SDIF直方图示例,真实PRI值为428μs(低于阈值),其谐波856μs超过阈值。
为避免"虚假"检测,需进行次谐波校验:首先找到直方图最大值,若该值未超过阈值,则检查第一个(最小的)超过阈值的数值。若对应的PRI值是直方图最大值对应的PRI值的某次谐波,则该值成为待执行序列搜索的潜在PRI;若超过阈值的最小PRI值不是直方图最大值PRI值的倍数,则从最小的超过阈值的PRI值开始,对所有超过阈值的PRI值执行序列搜索。这种谐波和次谐波分析也是对基本算法[1]的一种改进。
(iv)阈值的选择对于利用SDIF直方图实现辐射源的可靠、快速检测至关重要。阈值必须遵循过程的分布函数,以防止检测到大量"虚假"辐射源。下一部分将推导最优检测阈值函数。
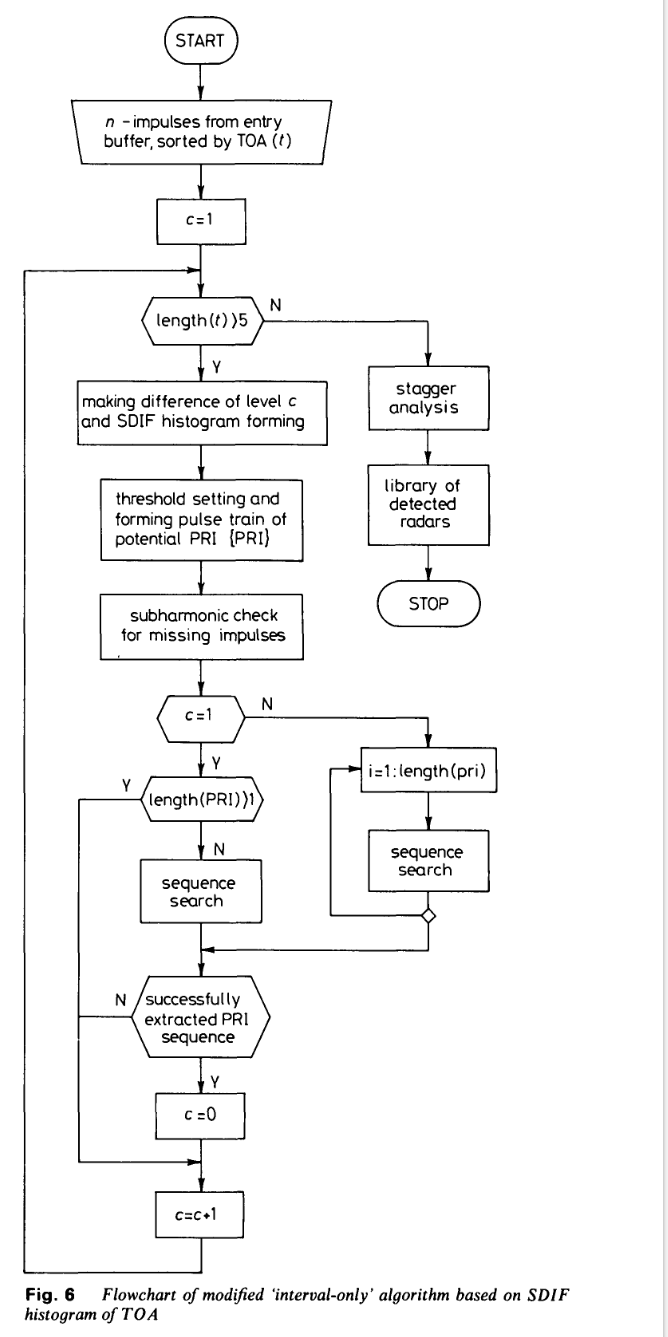
改进算法的流程图如图6所示。对于每个c级差值,构建SDIF直方图,计算阈值,经过次谐波校验后所有超过阈值的直方图数值均成为待序列搜索的潜在PRI。若PRI序列提取成功,则重复该过程直至提取出脉冲序列,或输入缓冲区中仅剩余5个脉冲;若序列搜索无法提取PRI序列,则计算下一个差值,设置新阈值并重复整个过程。PRI分析结束后,执行参差识别。
4 SDIF直方图的最优检测阈值
要确定哪个直方图峰值对应潜在脉冲重复间隔,需根据SDIF直方图的bins序号找到最优阈值函数。
显然,阈值与bins序号τ成反比。由于直方图中的bins对应脉冲之间的间隔,且观测时间是有限的,因此在有限观测时间内,脉冲间观测时间间隔越大,该间隔出现的次数越少。从数学角度,该阈值可表示为:
threshold(τ)=kτthreshold(\tau) = \frac{k}{\tau}threshold(τ)=τk
其中E为观测到的脉冲总数,x为小于1的常数。
若观测到的脉冲数量足够多,且多个辐射源同时工作,则相邻脉冲之间的间隔可视为随机事件,即脉冲的上升沿可视为随机泊松点[3],有限观测间隔T将其划分为n个子间隔。已知,n个随机分布的点中有k个落在长度为τ=t2−t1\tau = t_2 - t_1τ=t2−t1的间隔(t1−t2)(t_1 - t_2)(t1−t2)内的概率由泊松分布[3]给出:
pk(τ)=(λτ)kk!e−λτk=0,1,2,...p_k(\tau) = \frac{(\lambda \tau)^k}{k!} e^{-\lambda \tau} \quad k=0,1,2,...pk(τ)=k!(λτ)ke−λτk=0,1,2,...
式(2)的推导基于假设λ=n/T\lambda = n/Tλ=n/T,且n和T无限增大但比值λ保持恒定。
式(2)中,λ为泊松过程的参数,表示单位时间内的平均事件数。由于我们观测的是多个同时工作的辐射源的脉冲序列,因此接收的脉冲数与总观测时间成正比,即与直方图的总bins数N成正比。
一个泊松点落在间隔τ内的概率可由k=0时的上述表达式推导得出:相邻脉冲间间隔为τ的概率分布函数。换句话说,一阶差分的直方图将具有式(3)的形式。由于直方图是概率分布的估计,高阶差分也将呈指数形式;对于c级差异,由于构建该级直方图的脉冲数为E−cE - cE−c,因此直方图与间隔概率成正比。由于观测时间间隔与样本数(即直方图的总bins数)成正比,泊松过程的参数为λ=1/(kN)\lambda = 1/(kN)λ=1/(kN),其中k为小于1的正常数。因此,最优阈值函数为:
threshold(τ)=x(E−c)e−τ/(kN)(4)threshold(\tau) = x(E - c) e^{-\tau/(kN)} \quad (4)threshold(τ)=x(E−c)e−τ/(kN)(4)
综上,检测阈值的最优函数形式如下:其中E为脉冲总数,N为直方图的总bins数,c为差异等级。常数x和k的最优值通过实验确定。缺失脉冲出现的均匀概率分布实际上叠加在泊松分布上,因此过程的本质未发生改变,阈值形式仍遵循直方图峰值。因此,常数x取决于假设的最大脉冲缺失百分比。
表1为不同阈值下解交织算法的仿真结果。算法在PC386计算机上采用高级编程语言MATLAB进行仿真,处理器时间以浮点运算次数(flops)表示。解交织算法产生但在雷达环境中实际不存在的辐射源称为"虚假"辐射源。
表1 计算机仿真结果
| 阈值函数 | 成功检测的辐射源数量 | 虚假辐射源数量 | 处理器时间(flops) | ||||
|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | ||
| exp(−τ)exp(-\tau)exp(−τ) | 5 | 7 | 3 | 0 | 2 | 1 | 285K、341K、188K |
| 1/τ1/\tau1/τ | 3 | 2 | 1 | 5 | 10 | 2 | 823K、1.32M、514K |
| 常数 | 4 | 5 | 3 | 2 | 5 | 1 | 489K、827K、333K |
注:I=5部雷达(2部参差雷达、2部捷变频雷达、1部传统雷达);II=7部雷达(3部参差雷达、2部捷变频雷达、2部传统雷达);III=3部雷达(3部参差雷达和捷变频雷达)
显然,新的指数阈值效果更佳,因为指数函数最符合过程的本质。
图7为仿真中使用的不同形式的阈值函数。可以看出,新阈值与直方图峰值贴合度极高。
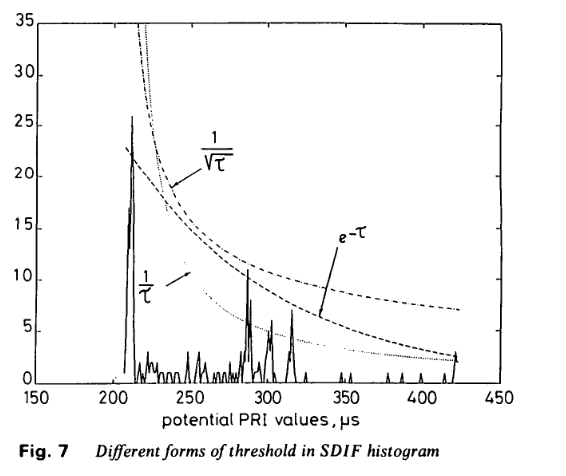
参考文献[1]中未讨论阈值函数,仅在图5和图6中展示了阈值。CDIF直方图[1]中的数值由之前的差值累积得到,因此决策阈值为指数函数的总和,其极限趋势应符合式(1)给出的1/τ1/\tau1/τ关系。这进一步验证了指数阈值的最优性。
采用新阈值后,分析时间大幅缩短,因为改进算法仅产生少量需执行序列搜索的虚假PRI值。此外,由于选择了指数阈值,仅需计算低阶差分,减少了直方图的数量,这也是新算法比原始算法[1]更快的另一个原因。
5 多参数解交织算法
前文所述的改进PRI分析可成功应用于多参数解交织算法[4,5,6,7],该算法中,PRI分析将在已按方位角(DOA)、频率(RF)、脉冲宽度(PW)或其他参数分类的脉冲组上执行。通过除到达时间外的其他脉冲参数,为高效解交织提供了新的可能。
参考文献[6]中,解交织过程分为两个阶段:方位角-射频滤波器将每个输入脉冲块划分为多个脉冲批次,然后通过TOA差值直方图对这些脉冲批次进行顺序处理,分解为单个脉冲链。所提出的方位角-射频滤波器作为一种二维算法,首先将脉冲分类到方位角桶中,然后利用射频值中的大间隙定义聚类。对于捷变频雷达,核心问题是距离阈值的最优选择,该阈值需避免将同一雷达的脉冲分割到不同组中,或形成过大的组。度量技术在方位角-射频滤波中起着重要作用。
参考文献[7]中提出的另外两种多参数算法也采用度量技术进行多维脉冲聚类,并通过加权反映每个参数的分辨能力,然后在这些聚类上计算TOA差值直方图。这些算法中的主要挑战是分离稳定雷达和捷变雷达,以及正确分组具有重叠特性的雷达。
考虑多参数解交织算法的主要目的并非开发新的、更高效的算法,而是研究新脉冲参数纳入解交织过程后的影响,并对比此类算法与第3节所述改进TOA解交织算法的速度和可靠性。
新算法中对其他脉冲参数的分析主要通过直方图进行。由于方位角的稳定性和可靠性[4],选择方位角作为最重要的解交织参数,并基于输入缓冲区中的所有脉冲构建方位角直方图。围绕每个直方图最大值聚类的脉冲对应不同的辐射源,因此需要根据方位角数值分离这些脉冲。
使用直方图时存在确定直方图组边界的问题。一种可行的解决方案是将平均直方图数值的局部最小值定义为组边界。然后,分离输入缓冲区中方位角相同或相似的脉冲,并将其分类到方位角组中。在每个方位角组内,需要分析下一个参数。
初看之下,选择频率作为第二个解交织参数是合理的[6],这样可以在方位角-频率空间中进行脉冲聚类。但对于捷变频雷达,频率聚类可能导致大量脉冲组的出现,进而产生"虚假"辐射源。在一个方位角组内将脉冲分类到频率组中,可能会丢失同一辐射源脉冲之间的相关性,导致PRI分析几乎无法进行。
众所周知,脉冲宽度和幅度是不可靠的参数,且不适用于解交织[4],因此选择到达时间作为第二个解交织参数。将改进后的PRI分析新算法用于每个检测到的方位角组内的精细脉冲聚类。
通过PRI分析,在每个方位角组内,将具有相同或相似PRI值的脉冲分类到PRI组中。为了更好地对检测到的辐射源进行分类,选择载波频率作为第三个解交织参数,即在每个PRI组内构建并分析频率直方图。
对于固定载波频率的雷达,频率直方图将产生单个显著峰值;若频率直方图中出现多个显著峰值,则可判定该辐射源为捷变频雷达。不进行频率聚类,频率直方图仅用于判断PRI组中的脉冲是否属于捷变频雷达。
最后执行参差分析。具有相同方位角、PRI和频率特征的提取脉冲组将被视为对应单个检测到的辐射源。该多参数算法的流程图如图8所示。
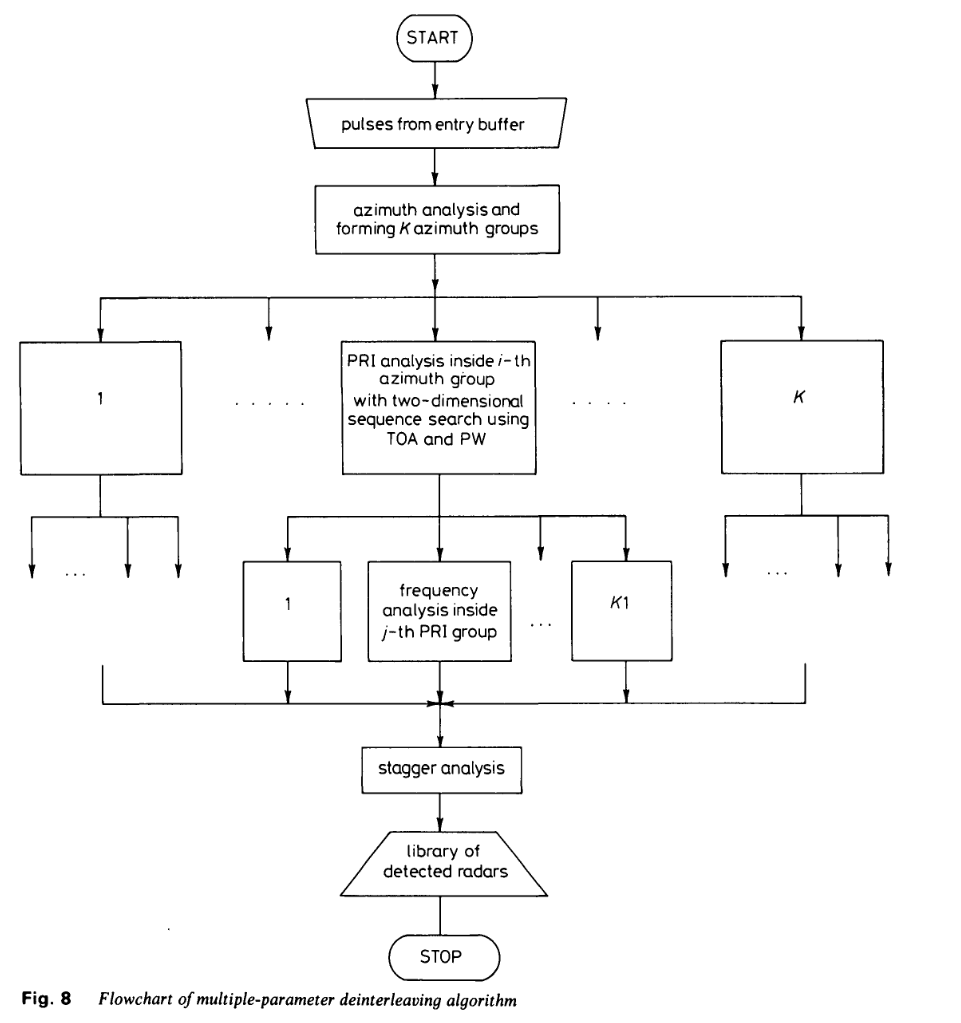
若在TOA解交织算法中引入二维序列搜索(同时分析脉冲宽度和到达时间),可进一步改进整体多参数算法的性能,即使在极高交错脉冲密度的情况下,也能确保可靠的PRI提取。尽管算法复杂度有所增加,但过程速度并未降低,反而提升了约1%。
对比第3节和第4节所述的改进TOA算法,多参数解交织算法在可靠性和速度方面的提升值得关注。仅使用到达时间进行解交织时,SDIF直方图基于输入缓冲区中的所有脉冲构建,且序列搜索在整个缓冲区上执行。由于所有接收脉冲均可用于分析,SDIF直方图技术具有良好的结果和高精度;但在高脉冲密度和大量交错信号的情况下,基于SDIF直方图的PRI分析变得复杂,辐射源检测的可靠性不再有保障。
通过方位角分析,输入缓冲区被划分为更小的脉冲组,每个组通过SDIF直方图技术进行分析,此时SDIF直方图的构建速度大幅提升;同时,由于脉冲数量较少,序列搜索速度也更快。在复杂雷达环境和大量脉冲的情况下,方位角聚类不仅能显著提升算法速度,还能提高辐射源分类的可靠性。
表2为基于MATLAB的计算机仿真结果,对比了两种解交织方法:仅基于间隔的算法(仅分析到达时间)和多参数算法(分析方位角(DOA)、到达时间(TOA)和载波频率(RF))。
多次算法测试经验表明,方位角是初始聚类的最佳参数,构建方位角组对算法速度的提升贡献最大。从表2可以看出,示例I(两部传统雷达)的速度提升约为70%,示例V(10部雷达:3部传统雷达、4部参差雷达、3部捷变频雷达)的速度提升约为300%。由此可得出结论:雷达环境越复杂,算法速度提升越显著。
交错雷达数量较少时,方位角聚类对辐射源分类可靠性的影响较小;但在复杂雷达环境中,可靠性仍会提升,如表2中最后一个示例(10部雷达)所示:仅基于间隔的算法成功检测到7部辐射源,产生10个虚假辐射源;而多参数算法成功检测到9部辐射源,仅产生3个虚假辐射源。
表2 计算机仿真结果
| 分析中使用的参数 | 成功检测的辐射源数量 | 虚假辐射源数量 | 处理器时间(flops) | ||||
|---|---|---|---|---|---|---|---|
| 传统 | 参差 | 捷变频 | 传统 | 参差 | 捷变频 | ||
| DOA、TOA、RF | 2 | 0 | 0 | 0 | 0 | 0 | 56271 |
| 仅TOA | 2 | 0 | 0 | 1 | 0 | 0 | 73432 |
| II DOA、TOA、RF | 1 | 1 | 2 | 0 | 0 | 1 | 137855 |
| 仅TOA | 1 | 1 | 2 | 0 | 0 | 0 | 292398 |
| III DOA、TOA、RF | 1 | 3 | 0 | 0 | 1 | 0 | 326212 |
| 仅TOA | 1 | 2 | 0 | 2 | 1 | 0 | 547892 |
| IV DOA、TOA、RF | 2 | 2 | 1 | 0 | 0 | 0 | 282097 |
| 仅TOA | 1 | 1 | 1 | 3 | 0 | 0 | 889325 |
| V DOA、TOA、RF | 3 | 4 | 3 | 1 | 2 | 0 | 623417 |
| 仅TOA | 2 | 3 | 2 | 6 | 2 | 2 | 1921313 |
注:I=2部雷达(2部传统雷达);II=4部雷达(1部传统雷达、1部参差雷达、2部捷变频雷达);III=4部雷达(1部传统雷达、3部参差雷达);IV=5部雷达(2部传统雷达、2部参差雷达、1部捷变频雷达);V=10部雷达(3部传统雷达、4部参差雷达、3部捷变频雷达)
从最后一个示例可以看出,新算法的结果略逊于之前的示例,原因在于所使用的序列搜索算法------参考文献[1]中的一维序列搜索算法。在极高脉冲密度的情况下,该算法会提取到达时间接近的不同辐射源的脉冲。若采用基于到达时间和脉冲宽度的二维序列搜索算法,可获得更好的结果。脉冲宽度作为序列搜索中的第二个参数,其主要作用是防止错误脉冲被提取到PRI序列中(脉冲宽度非常接近的情况除外)。
表3对比了在上述多参数算法中实现的两种序列搜索算法(一维和二维)。观测雷达环境包含10部雷达(输入缓冲区中有934个交错脉冲):3部传统雷达、3部捷变频雷达和4部参差雷达(等级分别为2、3、4、5)。解交织结果显示,两种情况下均成功检测到9部辐射源;一维序列搜索产生5个虚假辐射源(这些虚假辐射源来自未被检测到的5级参差雷达);二维序列搜索仅产生2个虚假辐射源。该环境比表2最后一个示例的环境更复杂,因为采用了更高的脉冲密度和参差等级。从表3可以看出,算法的可靠性和处理速度均有所提升。
表3 计算机仿真结果
| 序列搜索算法 | 解交织中使用的参数 | 成功检测的辐射源数量 | 虚假辐射源数量 | 处理器时间(flops) | ||||
|---|---|---|---|---|---|---|---|---|
| 传统 | 参差 | 捷变频 | 传统 | 参差 | 捷变频 | |||
| 一维 | DOA、TOA、RF | 3 | 3 | 3 | 4 | 1 | 0 | 679939 |
| 二维 | DOA、TOA、PW、RF | 3 | 3 | 3 | 1 | 1 | 0 | 674065 |
注:10部雷达的一维和二维序列搜索算法对比:3部传统雷达、4部参差雷达(等级2、3、4、5)、3部捷变频雷达
6 结论
本文提出了一种基于TOA分析(采用SDIF直方图)的改进雷达脉冲解交织算法,并将其应用于多参数解交织算法。
计算机仿真结果表明,基于TOA分析的所提算法表现优异,适用于传统雷达、参差雷达和捷变频雷达。多参数解交织算法(包含新的TOA SDIF直方图分析)可实现辐射源更可靠、更快的检测,尤其在复杂雷达环境中。若在TOA分析中引入基于到达时间和脉冲宽度的二维序列搜索算法,可进一步提升算法性能。
利用所有可用的脉冲参数(DOA、TOA、PW、RF)并在雷达信号检测和识别过程中采用多维算法,为开发高效解交织算法提供了广阔前景。
专业术语表
| 英文术语 | 中文译法 | 缩写 |
|---|---|---|
| Deinterleaving of radar pulses | 雷达脉冲解交织 | - |
| Sequential Difference Histogram | 序贯差分直方图 | SDIF |
| Cumulative Difference | 累积差分 | CDIF |
| Pulse Repetition Interval | 脉冲重复间隔 | PRI |
| Time of Arrival | 到达时间 | TOA |
| Angle of Arrival | 到达角 | AOA |
| Direction of Arrival | 方位角 | DOA |
| Carrier Frequency | 载波频率 | RF |
| Pulse Width | 脉冲宽度 | PW |
| Difference level | 差异等级 | - |
| Sequence search | 序列搜索 | - |
| Threshold function | 阈值函数 | - |
| Poisson distribution | 泊松分布 | - |
| Random jitter | 随机抖动 | - |
| Subharmonic checking | 次谐波校验 | - |
| Stagger recognition | 参差识别 | - |
| Emitter | 辐射源 | - |
| False emitters | 虚假辐射源 | - |
| Pulse clustering | 脉冲聚类 | - |
| Frequency-agile radar | 捷变频雷达 | - |
| Staggered PRI radar | 参差PRI雷达 | - |
| Classic radar | 传统雷达 | - |
| Interleaved pulses | 交错脉冲 | - |
| Processor time | 处理器时间 | - |
| Floating point operations | 浮点运算次数 | flops |
| Metric technique | 度量技术 | - |
| Stagger frame rate | 参差帧速率 | - |