除了传统通信之外,联合通信与感知 (JCAS) 作为下一代无线系统的关键赋能技术正变得日益重要。准确传输和接收数据的能力是高速通信和精确感知的基础,其中一个基本要求是精确的同相 (I) 和正交 (Q) 调制。对于感知而言,IQ 调制中的非理想特性会导致距离-多普勒图 (RDM) 中出现两个关键问题,表现为本底噪声升高和虚假目标的存在,从而降低了 RDM 中信息的准确性和可靠性。
本文提出了一种低复杂度的估计与补偿方法,以减轻 IQ 不平衡的影响。该方法主要通过利用泄漏信号来实现,其中泄漏信号(the leakage signal)是指从发射机到接收机路径的直达信号,通常是 RDM 中最强的信号分量。IQ 不平衡抑制结构的参数是基于混合复数/实数值双线性滤波器方法进行估计的,该方法考虑了 IQ 不平衡在具备 JCAS 能力的用户设备 (UE) 的发射机和接收机中。
用户设备 (UE) 使用符合 5G 新空口 (NR) 标准的正交频分复用 (OFDM) 波形,并且假设系统配置是由通信侧预先定义的。
Keywords: 5G compliant OFDM radar, IQ imbalance, JCAS, leakage
关键词: 符合 5G 标准的 OFDM 雷达,IQ 不平衡,JCAS,泄漏
"system configuration assumed to be predefined from the communication side":系统的参数(如子载波间隔、循环前缀长度、导频分布、帧结构等)是为了满足通信需求而确定的,感知功能(Sensing)只能被动接受这些参数。
在文献中,提出了不同的方法来减轻 JCAS 应用的 IQ 不平衡影响。
-
在 [11] 中,提出了一种调整发射波形的方法,使得基于 OFDM 的感知应用能够抵抗 IQ 不平衡。这是通过定义 OFDM 波形的设计准则来实现的(defining design criterions for the OFDM waveform),其中感知应用的最大不模糊距离减少了 222 倍,这取决于具体的感知应用和数据速率,通常是不可行的。
-
在此基础上,[12] 提出了一种新颖的基于 OFDM 的 JCAS 系统,该系统没有这种缺点,并同时考虑了 Tx 和 Rx 的 IQ 不平衡。这是通过将 RDM 中的虚假目标(由 IQ 不平衡导致的 RDM 中物体的副本)移动到不同的速度来实现的,在此处可以通过跟踪算法识别它们。
-
在 [13] 中,提出了一种基于 Rx 信号圆特性的方法来解决该问题。不幸的是,这种假设在存在强静止物体的情况下是不适用的,这激发了一种改进的 IQ 不平衡估计过程,即作为预处理步骤消除 RDM 中的强静止物体,这也是在 [13] 中提出的。
-
在 [14] 中,研究了一种接收机架构的设计,该架构使用两步迭代估计方法来估计信道冲激响应 (channel impulse response,CIR) 以及 Tx 和 Rx 的 IQ 不平衡。与其他工作相比,该方法仅需要短训练序列来估计 CIR 以及 IQ 不平衡参数。此外,据称这种迭代方法具有低计算复杂度。(Additionally, it is claimed that this iterative method has low computational complexity.)
-
在 [15] 中,提出了一种估计方法来估计 Tx 和 Rx 路径中的 IQ 不平衡。假设 Tx IQ 不平衡相对于 Rx IQ 不平衡较小。然而,这种假设在 UE 中许多情况下不成立,并限制了该方法的适用性。
由 Tx 到 Rx 路径的直接耦合引起的泄漏是感知应用中众所周知的挑战 [16]。对于调频连续波 (FMCW) 雷达系统,这种泄漏抑制可以通过在接收路径中使用 FMCW 发射信号进行下变频,随后进行高通滤波来执行 [17]。这种方法对于 OFDM 是不可能的,需要实际的对消过程来减轻这种影响 [16]。然而,这提供了利用以下事实的可能性,即泄漏是 UE 接收机中非常主导的信号,并且存在并包含 Tx 和 Rx 的 IQ 不平衡。
在本文中,提出了一种方法,利用接收机的泄漏和其他主导信号分量作为 [18] 中提出的混合复数/实数值双线性估计器的输入。估计得到的参数包含有关 Tx 和 Rx 通路中 IQ 不平衡的信息,随后应用于补偿过程,在该过程中重构真实的发射和接收信号以建模 IQ 不平衡的影响。随后进行标准的 OFDM 雷达处理,以实现精确的信道估计。为了验证所提出的方法,分析了受 IQ 不平衡影响的信道和补偿后信道的 RDM,并评估了对本底噪声升高的抑制以及虚假目标功率的降低。此外,在实际物体的位置评估了 RDM 中物体复振幅的重构,以确保该方法适用于高级信号处理任务,例如波达方向 (DOA) 估计。
对于这项工作,假设从 UE 的角度出发,这不允许像 [15] 中那样忽略 Tx 或 Rx 的 IQ 不平衡。我们假设一个符合 5G NR 标准的 OFDM 系统,其中波形生成基于填充了随机生成的数据符号的完全分配的物理上行共享信道 (PUSCH) 资源网格。在本研究中,波形被认为是由通信过程决定的,这使得 [11--13] 中提出的波形调整不再适用。[14] 中提出的估计 CIR 以及 Tx 和 Rx IQ 不平衡的迭代算法满足所有假设,并被用作对比算法。
2 OFDM-Based Sensing
3 IQ Imbalance
3.1 Tx and Rx IQ Imbalance
本小节对图 1 所示系统中的 IQ 不平衡效应进行了数学推导。为了便于说明,对每个 OFDM 符号单独建模 IQ 不平衡。因此,单个 OFDM 符号受 IQ 不平衡影响的 Tx 数据向量 yTx\mathbf{y}_{\text{Tx}}yTx 在频域表示为
yTx=αTxxTx+βTxx‾Tx∗,(8) \mathbf{y}{\text{Tx}} = \alpha{\text{Tx}}\mathbf{x}{\text{Tx}} + \beta{\text{Tx}}\underline{\mathbf{x}}_{\text{Tx}}^*, \tag{8} yTx=αTxxTx+βTxxTx∗,(8)
其中 xTx\mathbf{x}{\text{Tx}}xTx 是 Tx 资源网格 XTx\mathbf{X}{\text{Tx}}XTx 中的任意一个 OFDM 符号,Tx 通路 IQ 不平衡由 FID 不平衡参数 αTx\alpha_{\text{Tx}}αTx 和 βTx\beta_{\text{Tx}}βTx 表征。经过频域信道 h\mathbf{h}h 和加性高斯白噪声 (AWGN) n∼CN(0,σ2INsc)\mathbf{n} \sim \mathcal{CN}(\mathbf{0}, \sigma^2\mathbf{I}{N{\text{sc}}})n∼CN(0,σ2INsc)(其中 σ2\sigma^2σ2 为噪声方差,INsc\mathbf{I}{N{\text{sc}}}INsc 为尺寸 Nsc×NscN_{\text{sc}} \times N_{\text{sc}}Nsc×Nsc 的单位矩阵)作用后,不含 Rx IQ 不平衡的 Rx 数据向量表示为
xRx=(αTxxTx+βTxx‾Tx∗)∘h+n.(9) \mathbf{x}{\text{Rx}} = (\alpha{\text{Tx}}\mathbf{x}{\text{Tx}} + \beta{\text{Tx}}\underline{\mathbf{x}}_{\text{Tx}}^*) \circ \mathbf{h} + \mathbf{n}. \tag{9} xRx=(αTxxTx+βTxxTx∗)∘h+n.(9)
引入 Rx IQ 不平衡后得到
yRx=αRxαTxxTx∘h+αRxβTxx‾Tx∗∘h+αRxn+βRxαTx∗x‾Tx∗∘h‾∗+βRxβTx∗xTx∘h‾∗+βRxn‾∗,(10) \begin{aligned} \mathbf{y}{\text{Rx}} &= \alpha{\text{Rx}}\alpha_{\text{Tx}}\mathbf{x}{\text{Tx}} \circ \mathbf{h} + \alpha{\text{Rx}}\beta_{\text{Tx}}\underline{\mathbf{x}}{\text{Tx}}^* \circ \mathbf{h} + \alpha{\text{Rx}}\mathbf{n} \\ &\quad + \beta_{\text{Rx}}\alpha_{\text{Tx}}^*\underline{\mathbf{x}}{\text{Tx}}^* \circ \underline{\mathbf{h}}^* + \beta{\text{Rx}}\beta_{\text{Tx}}^*\mathbf{x}{\text{Tx}} \circ \underline{\mathbf{h}}^* + \beta{\text{Rx}}\underline{\mathbf{n}}^*, \end{aligned} \tag{10} yRx=αRxαTxxTx∘h+αRxβTxxTx∗∘h+αRxn+βRxαTx∗xTx∗∘h∗+βRxβTx∗xTx∘h∗+βRxn∗,(10)
其中 Rx 通路的 FID IQ 不平衡参数分别为 αRx\alpha_{\text{Rx}}αRx 和 βRx\beta_{\text{Rx}}βRx。
为了恢复受 IQ 不平衡影响的信道向量 hIQ\mathbf{h}_{\text{IQ}}hIQ,将 Rx OFDM 符号与 Tx OFDM 符号进行逐元素相除,即
hIQ=yRx⊘xTx,=αRxαTxh+αRxβTxxTx′∘h+βRxαTx∗xTx′∘h‾∗+βRxβTx∗h‾∗+(αRxn+βRxn‾∗)⊘xTx. \begin{align} \mathbf{h}{\text{IQ}} &= \mathbf{y}{\text{Rx}} \oslash \mathbf{x}{\text{Tx}}, \tag{11} \\ &= \alpha{\text{Rx}}\alpha_{\text{Tx}}\mathbf{h} + \alpha_{\text{Rx}}\beta_{\text{Tx}}\mathbf{x}'{\text{Tx}} \circ \mathbf{h} + \beta{\text{Rx}}\alpha_{\text{Tx}}^*\mathbf{x}'{\text{Tx}} \circ \underline{\mathbf{h}}^* \nonumber\\ &\quad + \beta{\text{Rx}}\beta_{\text{Tx}}^*\underline{\mathbf{h}}^* + (\alpha_{\text{Rx}}\mathbf{n} + \beta_{\text{Rx}}\underline{\mathbf{n}}^*) \oslash \mathbf{x}_{\text{Tx}}. \tag{12} \end{align} hIQ=yRx⊘xTx,=αRxαTxh+αRxβTxxTx′∘h+βRxαTx∗xTx′∘h∗+βRxβTx∗h∗+(αRxn+βRxn∗)⊘xTx.(11)(12)
注意其中 xTx′=x‾Tx∗⊘xTx\mathbf{x}'{\text{Tx}} = \underline{\mathbf{x}}{\text{Tx}}^* \oslash \mathbf{x}_{\text{Tx}}xTx′=xTx∗⊘xTx
3.2 Effects of IQ Imbalance on Sensing Applications
分析公式 (12) 时,可以看出
-
第一项提供了所需的信道向量 h\mathbf{h}h,并被因子 αRxαTx\alpha_{\text{Rx}}\alpha_{\text{Tx}}αRxαTx 缩放(在合理的 IQ 不平衡假设下,该因子通常接近 1)。
-
此外,真实信道 h\mathbf{h}h 的复共轭镜像版本也被缩放因子 βRxβTx∗\beta_{\text{Rx}}\beta_{\text{Tx}}^*βRxβTx∗ 缩放并存在于公式 (12) 中。
- 由于复共轭作用,该项可能会在 RDM 中的负速度处引起一个虚假目标。对于合理的 IQ 不平衡值,其缩放项通常接近于零。因此,RDM 中对应的峰值通常可以忽略。
- 然而,如果它不可忽略,正如文献 [12] 中所论证的,该目标可以很容易地被跟踪算法识别为虚假目标,因此不是本文的主要关注点。
-
除了 AWGN 项之外,还出现了两个依赖于 xTx′\mathbf{x}'_{\text{Tx}}xTx′ 的附加项,由于载波间干扰 (ICI) 导致 RDM 中的本底噪声升高。请注意,已知的 Tx 数据是这种本底噪声升高的来源。
在图 2 中,展示了基于上述 OFDM 感知过程的示例速度谱。仿真设置模拟了一个场景,其中
- 在 0 m 距离和 0 m/s 速度处存在主导泄漏,
- 在 6 m 和 15 m/s 处存在一个较弱的物体。
归一化功率电平分别为 0 dB 和 −20 dB。
AWGN 是根据 30 dB 的信噪比 (SNR) 生成的。这些场景参数用于说明目的,没有实际参考意义。选择它们是为了特别突出 RDM 中 IQ 不平衡的影响。IQ 不平衡参数也是如此。在图 2 中,可以观察到真实物体、其在负速度处对应的虚假目标以及升高的本底噪声,这可能会掩盖 RDM 中较弱的物体。与真实物体相比,虚假目标被所谓的镜像抑制比 (image suppression ratio,ISR) 衰减,ISR 给出为
ISR=10log(∣αTxαRx∣2∣βRxβTx∗∣2)(13) \text{ISR} = 10 \log \left( \frac{|\alpha_{\text{Tx}}\alpha_{\text{Rx}}|^2}{|\beta_{\text{Rx}}\beta_{\text{Tx}}^*|^2} \right) \tag{13} ISR=10log(∣βRxβTx∗∣2∣αTxαRx∣2)(13)
对于此特定参数设置,其值为 20 dB。
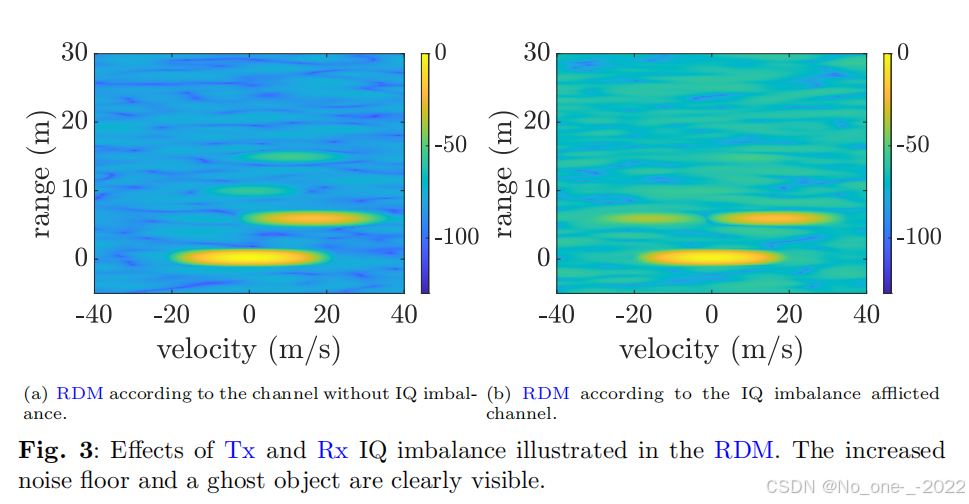
在图 3 中,展示了 a) 无 IQ 不平衡的信道和 b) 受 IQ 不平衡影响的信道的 RDM。对于这个示例场景(与图 2 中的场景不同),存在一个主导泄漏和三个额外的较弱物体。在图 3b 中,可以清楚地观察到由于 IQ 不平衡导致的本底噪声升高以及虚假目标。
4 Parameter Estimation via Bilinear Filters
在 [18] 中,提出了复数值双线性滤波器,构成了本文推导的估计方法的基础。在 3.2 节中,讨论了 (12) 的不同项。观察到,所描述的 ICI 是本底噪声升高的基础。最主要的主导信号分量对该效应有主要影响。因此,在本文中,为了估计 IQ 不平衡参数(αTx,βTx,αRx,βRx\alpha_{\text{Tx}}, \beta_{\text{Tx}}, \alpha_{\text{Rx}}, \beta_{\text{Rx}}αTx,βTx,αRx,βRx),我们首先找到了信号中最强的成分(主导振荡,即泄漏),提取其参数并人工重构了一个理想的信道矩阵(a synthetically generated channel matrix),然后基于这个合成矩阵来进行估算。
特别是在以用户设备 (UE) 为核心的 JCAS 系统中,最强的反射信号通常是内部泄漏(例如由天线隔离度不足引起,insufficient antenna isolation)。本文特意利用了(is explicitly exploited)这一非理想特性,将其作为获取信道矩阵 H\mathbf{H}H 初步估计(记为 H~\tilde{\mathbf{H}}H~)的基础,具体步骤如下:
- 根据 (3) 推导受 IQ 不平衡影响的信道矩阵 H\mathbf{H}H。
- 应用恒虚警率 (CFAR) 算法来识别远高于本底噪声的主导峰值。
- 在后续考虑中忽略可能是更强峰值的虚假目标的峰值。
- 估计所考虑峰值的距离、相对速度和复振幅。在本文中,RELAX 方法 [23, 24] 因其准确性和低计算复杂度而被用于此任务。
- 使用这些估计值来合成重构信道矩阵 H~\tilde{\mathbf{H}}H~。
下面将介绍双线性滤波器(the bilinear filters)的推导和行为。
4.1 Bilinear Model
来自 (12) 的受 IQ 不平衡影响的信道 hIQ\mathbf{h}_{\text{IQ}}hIQ 可以重写以匹配 [18] 中的双线性模型,即
hIQ,i=fHXig+n~i,(14) h_{\text{IQ},i} = \mathbf{f}^{\text{H}}\mathbf{X}_i\mathbf{g} + \tilde{n}_i, \tag{14} hIQ,i=fHXig+n~i,(14)
hIQ,i⏟观测到的脏数据≈fH×Xi(H~)⏟用替身算出的已知矩阵×g\underbrace{h_{\text{IQ},i}}_{\text{观测到的脏数据}} \approx \mathbf{f}^{\text{H}} \times \underbrace{\mathbf{X}i(\tilde{\mathbf{H}})}{\text{用替身算出的已知矩阵}} \times \mathbf{g}观测到的脏数据 hIQ,i≈fH×用替身算出的已知矩阵 Xi(H~)×g
其中 f\mathbf{f}f 和 g\mathbf{g}g 是参数向量,噪声由 n~i\tilde{n}_in~i 表示,Xi\mathbf{X}_iXi 是具有匹配维度的已知系统矩阵。可得
hIQ,i=[αRx βRx]⏟fH[h~ijh~ih~i[xTx′]ijh~i[xTx′]i[h~∗]i[xTx′]i−j[h~∗]i[xTx′]i[h~∗]i−j[h~∗]i]⏟Xi[ℜ(αTx)ℑ(αTx)ℜ(βTx)ℑ(βTx)]⏟g+n~i,(15) h_{\text{IQ},i} = \underbrace{[\alpha_{\text{Rx}} \ \beta_{\text{Rx}}]}_{\mathbf{f}^{\text{H}}} \underbrace{\begin{bmatrix} \tilde{h}_i & j\tilde{h}_i & \tilde{h}i[\mathbf{x}'{\text{Tx}}]_i & j\tilde{h}i[\mathbf{x}'{\text{Tx}}]i \\ [\tilde{\mathbf{h}}^*]i[\mathbf{x}'{\text{Tx}}]i & -j[\tilde{\mathbf{h}}^*]i[\mathbf{x}'{\text{Tx}}]i & [\tilde{\mathbf{h}}^*]i & -j[\tilde{\mathbf{h}}^*]i \end{bmatrix}}{\mathbf{X}i} \underbrace{\begin{bmatrix} \Re(\alpha{\text{Tx}}) \\ \Im(\alpha{\text{Tx}}) \\ \Re(\beta{\text{Tx}}) \\ \Im(\beta{\text{Tx}}) \end{bmatrix}}{\mathbf{g}} + \tilde{n}_i, \tag{15} hIQ,i=fH [αRx βRx]Xi [h~i[h~∗]i[xTx′]ijh~i−j[h~∗]i[xTx′]ih~i[xTx′]i[h~∗]ijh~i[xTx′]i−j[h~∗]i]g ℜ(αTx)ℑ(αTx)ℜ(βTx)ℑ(βTx) +n~i,(15)
其中参数向量 f∈C2\mathbf{f} \in \mathbb{C}^2f∈C2 和参数向量 g∈R4\mathbf{g} \in \mathbb{R}^4g∈R4 分别对应于 Rx 和 Tx IQ 不平衡参数。噪声项 n~i\tilde{n}in~i 代表 (αRxni+βRx[n‾∗]i)⊘xTx(\alpha{\text{Rx}}n_i + \beta_{\text{Rx}}[\underline{\mathbf{n}}^*]i) \oslash \mathbf{x}{\text{Tx}}(αRxni+βRx[n∗]i)⊘xTx,并在随后的推导中被忽略,因为它不会改变算法,只会使方程变长。然而,在本文后续的所有仿真中都考虑了该项。
对于 (15) 中具有实数值 g\mathbf{g}g 和复数值 f\mathbf{f}f 的双线性模型,[18] 中推导了几种适用的双线性滤波器,包括双线性最小均方 (LMS) 滤波器、双线性归一化 LMS (NLMS) 滤波器、双线性交替维纳滤波器 (AWF)、双线性迭代维纳滤波器 (IWF) 以及双线性递归最小二乘 (RLS) 滤波器。这些滤波器的共同点是,它们在固定 g^\hat{\mathbf{g}}g^ 的情况下迭代估计 f\mathbf{f}f,随后在固定 f^\hat{\mathbf{f}}f^ 的情况下估计 g\mathbf{g}g。与样本自适应双线性滤波器 LMS、NLMS 和 RLS 相比,维纳滤波器执行迭代操作。通过双线性 LMS 滤波器的更新方程示例性地展示了这一点,其中
f^i=f^i−1+μfei∗Xig^i−1,(16) \hat{\mathbf{f}}i = \hat{\mathbf{f}}{i-1} + \mu_f e_i^* \mathbf{X}i \hat{\mathbf{g}}{i-1}, \tag{16} f^i=f^i−1+μfei∗Xig^i−1,(16)
和
g^i=g^i−1+μg2ℜ{eiXiHf^i−1},(17) \hat{\mathbf{g}}i = \hat{\mathbf{g}}{i-1} + \mu_g 2 \Re \left\{ e_i \mathbf{X}i^{\text{H}} \hat{\mathbf{f}}{i-1} \right\}, \tag{17} g^i=g^i−1+μg2ℜ{eiXiHf^i−1},(17)
其中 μf\mu_fμf 和 μg\mu_gμg 是步长,ei=hIQ,i−f^i−1HXig^i−1e_i = h_{\text{IQ},i} - \hat{\mathbf{f}}{i-1}^{\text{H}} \mathbf{X}i \hat{\mathbf{g}}{i-1}ei=hIQ,i−f^i−1HXig^i−1 是受 IQ 不平衡影响的信道 hIQ\mathbf{h}{\text{IQ}}hIQ 的第 iii 个元素与对应于第 iii 次估计的双线性模型产生的结果之间的误差。
从公式 (12) 到 (14) 的推导过程:双线性形式变换
该过程通过变量分离和参数展开,将非线性耦合方程转换为双线性形式。主要包含两个步骤:提取 Rx 参数形成向量 f\mathbf{f}f,以及将 Tx 参数展开为实部和虚部形成向量 g\mathbf{g}g。
单个元素 iii 的标量形式整理
根据公式 (12),忽略噪声项,第 iii 个子载波元素 hIQ,ih_{\text{IQ},i}hIQ,i 表示为:
hIQ,i=αRxαTxhi+αRxβTxxi′hi+βRxαTx∗xi′hi∗+βRxβTx∗hi∗ h_{\text{IQ},i} = \alpha_{\text{Rx}}\alpha_{\text{Tx}}h_i + \alpha_{\text{Rx}}\beta_{\text{Tx}}x'i h_i + \beta{\text{Rx}}\alpha_{\text{Tx}}^* x'i h^*i + \beta{\text{Rx}}\beta{\text{Tx}}^* h^*_i hIQ,i=αRxαTxhi+αRxβTxxi′hi+βRxαTx∗xi′hi∗+βRxβTx∗hi∗注:hih_ihi 对应合成信道 h~i\tilde{h}_ih~i,hi∗h^*_ihi∗ 对应 h‾∗\underline{\mathbf{h}}^*h∗ 的第 iii 个元素。
按 Rx 参数 (αRx,βRx\alpha_{\text{Rx}}, \beta_{\text{Rx}}αRx,βRx) 分组
为构造 fH\mathbf{f}^{\text{H}}fH,提取 αRx\alpha_{\text{Rx}}αRx 和 βRx\beta_{\text{Rx}}βRx 作为公因式:
hIQ,i=αRx⏟Rx部分 1(αTxhi+βTxxi′hi)+βRx⏟Rx部分 2(αTx∗xi′hi∗+βTx∗hi∗) h_{\text{IQ},i} = \underbrace{\alpha_{\text{Rx}}}{\text{Rx部分 1}} \left( \alpha{\text{Tx}}h_i + \beta_{\text{Tx}}x'i h_i \right) + \underbrace{\beta{\text{Rx}}}{\text{Rx部分 2}} \left( \alpha{\text{Tx}}^* x'_i h^*i + \beta{\text{Tx}}^* h^*_i \right) hIQ,i=Rx部分 1 αRx(αTxhi+βTxxi′hi)+Rx部分 2 βRx(αTx∗xi′hi∗+βTx∗hi∗)对应向量形式:[αRx,βRx]×[Tx相关项1Tx相关项2] [\alpha_{\text{Rx}}, \beta_{\text{Rx}}] \times \begin{bmatrix} \text{Tx相关项1} \\ \text{Tx相关项2} \end{bmatrix} [αRx,βRx]×[Tx相关项1Tx相关项2]
Tx 参数的实部虚部展开
利用复数性质 z=ℜ(z)+jℑ(z)z = \Re(z) + j\Im(z)z=ℜ(z)+jℑ(z) 及 z∗=ℜ(z)−jℑ(z)z^* = \Re(z) - j\Im(z)z∗=ℜ(z)−jℑ(z) 展开括号内 Tx 参数。
分析 αRx\alpha_{\text{Rx}}αRx 对应项(矩阵第一行):
项1=αTxhi+βTxxi′hi=(ℜ(αTx)+jℑ(αTx))hi+(ℜ(βTx)+jℑ(βTx))xi′hi=hiℜ(αTx)+jhiℑ(αTx)+hixi′ℜ(βTx)+jhixi′ℑ(βTx) \begin{aligned} \text{项1} &= \alpha_{\text{Tx}}h_i + \beta_{\text{Tx}}x'i h_i \\ &= (\Re(\alpha{\text{Tx}}) + j\Im(\alpha_{\text{Tx}}))h_i + (\Re(\beta_{\text{Tx}}) + j\Im(\beta_{\text{Tx}}))x'i h_i \\ &= h_i \Re(\alpha{\text{Tx}}) + j h_i \Im(\alpha_{\text{Tx}}) + h_i x'i \Re(\beta{\text{Tx}}) + j h_i x'i \Im(\beta{\text{Tx}}) \end{aligned} 项1=αTxhi+βTxxi′hi=(ℜ(αTx)+jℑ(αTx))hi+(ℜ(βTx)+jℑ(βTx))xi′hi=hiℜ(αTx)+jhiℑ(αTx)+hixi′ℜ(βTx)+jhixi′ℑ(βTx)
系数: hi, jhi, hixi′, jhixi′h_i, \ j h_i, \ h_i x'_i, \ j h_i x'_ihi, jhi, hixi′, jhixi′分析 βRx\beta_{\text{Rx}}βRx 对应项(矩阵第二行):
由于包含共轭 αTx∗\alpha_{\text{Tx}}^*αTx∗ 和 βTx∗\beta_{\text{Tx}}^*βTx∗,虚部符号为负:
项2=αTx∗xi′hi∗+βTx∗hi∗=(ℜ(αTx)−jℑ(αTx))xi′hi∗+(ℜ(βTx)−jℑ(βTx))hi∗=xi′hi∗ℜ(αTx)−jxi′hi∗ℑ(αTx)+hi∗ℜ(βTx)−jhi∗ℑ(βTx) \begin{aligned} \text{项2} &= \alpha_{\text{Tx}}^* x'i h^*i + \beta{\text{Tx}}^* h^*i \\ &= (\Re(\alpha{\text{Tx}}) - j\Im(\alpha{\text{Tx}}))x'i h^*i + (\Re(\beta{\text{Tx}}) - j\Im(\beta{\text{Tx}})) h^*_i \\ &= x'_i h^*i \Re(\alpha{\text{Tx}}) - j x'_i h^*i \Im(\alpha{\text{Tx}}) + h^*i \Re(\beta{\text{Tx}}) - j h^*i \Im(\beta{\text{Tx}}) \end{aligned} 项2=αTx∗xi′hi∗+βTx∗hi∗=(ℜ(αTx)−jℑ(αTx))xi′hi∗+(ℜ(βTx)−jℑ(βTx))hi∗=xi′hi∗ℜ(αTx)−jxi′hi∗ℑ(αTx)+hi∗ℜ(βTx)−jhi∗ℑ(βTx)
系数: xi′hi∗, −jxi′hi∗, hi∗, −jhi∗x'_i h^*_i, \ -j x'_i h^*_i, \ h^*_i, \ -j h^*_ixi′hi∗, −jxi′hi∗, hi∗, −jhi∗组装矩阵形式 (14) 和 (15)
将上述系数填入矩阵 Xi\mathbf{X}iXi,实虚部填入向量 g\mathbf{g}g,得到双线性模型:
hIQ,i=[αRx βRx]⏟fH×Xi×[ℜ(αTx)ℑ(αTx)ℜ(βTx)ℑ(βTx)]⏟g h{\text{IQ},i} = \underbrace{[\alpha_{\text{Rx}} \ \beta_{\text{Rx}}]}{\mathbf{f}^{\text{H}}} \times \mathbf{X}i \times \underbrace{\begin{bmatrix} \Re(\alpha{\text{Tx}}) \\ \Im(\alpha{\text{Tx}}) \\ \Re(\beta_{\text{Tx}}) \\ \Im(\beta_{\text{Tx}}) \end{bmatrix}}_{\mathbf{g}} hIQ,i=fH [αRx βRx]×Xi×g ℜ(αTx)ℑ(αTx)ℜ(βTx)ℑ(βTx)
其中 Xi\mathbf{X}_iXi 结构如下:
Xi=[h~ijh~ih~i[xTx′]ijh~i[xTx′]i[h~∗]i[xTx′]i−j[h~∗]i[xTx′]i[h~∗]i−j[h~∗]i] \mathbf{X}_i = \begin{bmatrix} \tilde{h}_i & j\tilde{h}_i & \tilde{h}i[\mathbf{x}'{\text{Tx}}]_i & j\tilde{h}i[\mathbf{x}'{\text{Tx}}]_i \\ [\tilde{\mathbf{h}}^*]i[\mathbf{x}'{\text{Tx}}]_i & -j[\tilde{\mathbf{h}}^*]i[\mathbf{x}'{\text{Tx}}]_i & [\tilde{\mathbf{h}}^*]_i & -j[\tilde{\mathbf{h}}^*]_i \end{bmatrix} Xi=[h~i[h~∗]i[xTx′]ijh~i−j[h~∗]i[xTx′]ih~i[xTx′]i[h~∗]ijh~i[xTx′]i−j[h~∗]i]
4.3 Ambiguity of the Estimation Process
使用 (14) 的双线性模型,可以看出对于给定的 Xi\mathbf{X}_iXi,估计值 f^\hat{\mathbf{f}}f^ 和 g^\hat{\mathbf{g}}g^ 不是唯一的。这可以通过扩展方程来说明,如下所示
hIQ,i=λf^HXig^1λ∗,(20) h_{\text{IQ},i} = \lambda\hat{\mathbf{f}}^{\text{H}}\mathbf{X}_i\hat{\mathbf{g}}\frac{1}{\lambda^*}, \tag{20} hIQ,i=λf^HXig^λ∗1,(20)
其中 λ∈C\lambda \in \mathbb{C}λ∈C 是一个任意复数因子,满足 λ≠0\lambda \neq 0λ=0。因此,双线性模型的相同输出可以用一个缩放的 f^\hat{\mathbf{f}}f^ 和一个反向缩放的 g^\hat{\mathbf{g}}g^ 来描述。有趣的是,对于 (15) 中推导出的双线性模型,结果表明可以识别出的不是一个,而是两个密切相关的缩放因子,如下所示。为了推导,(15) 给出了通用的矩阵和向量元素 xi,fix_i, f_ixi,fi 和 gig_igi(with general matrix and vector elements),以限制方程的长度
hIQ,i=[f1∗ f2∗][x1jx1x2jx2x3−jx3x4−jx4][ℜ(g1)ℑ(g1)ℜ(g2)ℑ(g2)].(21) h_{\text{IQ},i} = [f_1^* \ f_2^*] \begin{bmatrix} x_1 & jx_1 & x_2 & jx_2 \\ x_3 & -jx_3 & x_4 & -jx_4 \end{bmatrix} \begin{bmatrix} \Re(g_1) \\ \Im(g_1) \\ \Re(g_2) \\ \Im(g_2) \end{bmatrix}. \tag{21} hIQ,i=[f1∗ f2∗][x1x3jx1−jx3x2x4jx2−jx4] ℜ(g1)ℑ(g1)ℜ(g2)ℑ(g2) .(21)
通过用 λ1\lambda_1λ1 缩放 f1∗f_1^*f1∗ 并用 λ2\lambda_2λ2 缩放 f2∗f_2^*f2∗,(21) 可以写为
hIQ,i=[λ1f1∗ λ2f2∗][x1jx1x2jx2x3−jx3x4−jx4][ℜ(g~1)ℑ(g~1)ℜ(g~2)ℑ(g~2)],(22) h_{\text{IQ},i} = [\lambda_1 f_1^* \ \lambda_2 f_2^*] \begin{bmatrix} x_1 & jx_1 & x_2 & jx_2 \\ x_3 & -jx_3 & x_4 & -jx_4 \end{bmatrix} \begin{bmatrix} \Re(\tilde{g}_1) \\ \Im(\tilde{g}_1) \\ \Re(\tilde{g}_2) \\ \Im(\tilde{g}_2) \end{bmatrix}, \tag{22} hIQ,i=[λ1f1∗ λ2f2∗][x1x3jx1−jx3x2x4jx2−jx4] ℜ(g~1)ℑ(g~1)ℜ(g~2)ℑ(g~2) ,(22)
其中 g~1\tilde{g}_1g~1 和 g~2\tilde{g}_2g~2 为未知参数。将展示可以通过选择 g~1\tilde{g}_1g~1 和 g~2\tilde{g}_2g~2 作为 g1g_1g1 和 g2g_2g2 的缩放版本(使用适当选择的缩放因子)来补偿 f1f_1f1 和 f2f_2f2 的缩放。重写 (21) 和 (22) 并令它们相等,可产生
hIQ,i=f1∗x1g1+f1∗x2g2+f2∗x3g1∗+f2∗x4g2∗=λ1f1∗x1g~1+λ1f1∗x2g~2+λ2f2∗x3g~1∗+λ2f2∗x4g~2∗(23) \begin{aligned} h_{\text{IQ},i} &= f_1^* x_1 g_1 + f_1^* x_2 g_2 + f_2^* x_3 g_1^* + f_2^* x_4 g_2^* \\ &= \lambda_1 f_1^* x_1 \tilde{g}_1 + \lambda_1 f_1^* x_2 \tilde{g}_2 + \lambda_2 f_2^* x_3 \tilde{g}_1^* + \lambda_2 f_2^* x_4 \tilde{g}_2^* \end{aligned} \tag{23} hIQ,i=f1∗x1g1+f1∗x2g2+f2∗x3g1∗+f2∗x4g2∗=λ1f1∗x1g~1+λ1f1∗x2g~2+λ2f2∗x3g~1∗+λ2f2∗x4g~2∗(23)
得到
g~1=g11λ1, g~2=g21λ1, g~1∗=g1∗1λ2, g~2∗=g2∗1λ2.(24) \tilde{g}_1 = g_1 \frac{1}{\lambda_1}, \ \tilde{g}_2 = g_2 \frac{1}{\lambda_1}, \ \tilde{g}_1^* = g_1^* \frac{1}{\lambda_2}, \ \tilde{g}_2^* = g_2^* \frac{1}{\lambda_2}. \tag{24} g~1=g1λ11, g~2=g2λ11, g~1∗=g1∗λ21, g~2∗=g2∗λ21.(24)
这表明如果 λ1\lambda_1λ1 等于 λ2∗\lambda_2^*λ2∗,则等式成立,并证明了 IQ 不平衡参数在双线性估计过程后是模糊的(are ambiguous after the bilinear estimation process),然而,受 IQ 不平衡影响的信道 hIQ\mathbf{h}_{\text{IQ}}hIQ 不受这种模糊性的影响,因为这些缩放因子相互抵消了。f\mathbf{f}f 和 g\mathbf{g}g 中的缩放参数被传递给随后讨论的补偿方法,以减轻 RDM 中的 IQ 不平衡影响。将会展示,增加的本底噪声可以被大幅降低。
The scaled parameters in f\mathbf ff and g\mathbf gg are passed to the subsequently discussed compensation approach to mitigate the IQ imbalance effects in the RDM.
5 Compensation Strategy
继上一节的参数估计过程之后,本节描述如图 5 所示的补偿策略。考虑到所有 NsymN_{\text{sym}}Nsym 个 OFDM 符号,利用估计出的 Tx IQ 不平衡参数,将频域数据矩阵 XTx\mathbf{X}{\text{Tx}}XTx 变换为 Y^Tx\hat{\mathbf{Y}}{\text{Tx}}Y^Tx,通过
Y^Tx=α^TxXTx+β^TxX‾Tx∗.(25) \hat{\mathbf{Y}}{\text{Tx}} = \hat{\alpha}{\text{Tx}}\mathbf{X}{\text{Tx}} + \hat{\beta}{\text{Tx}}\underline{\mathbf{X}}_{\text{Tx}}^*. \tag{25} Y^Tx=α^TxXTx+β^TxXTx∗.(25)
对于 Rx 通路,可得
YRx=α^RxX^Rx+β^RxX‾^Rx∗,(26) \mathbf{Y}{\text{Rx}} = \hat{\alpha}{\text{Rx}}\hat{\mathbf{X}}{\text{Rx}} + \hat{\beta}{\text{Rx}}\hat{\underline{\mathbf{X}}}_{\text{Rx}}^*, \tag{26} YRx=α^RxX^Rx+β^RxX^Rx∗,(26)
及其复共轭镜像版本(its complex conjugated and mirrored version)可以通过下式计算
Y‾Rx∗=α^Rx∗X‾^Rx∗+β^Rx∗X^Rx.(27) \underline{\mathbf{Y}}{\text{Rx}}^* = \hat{\alpha}{\text{Rx}}^*\hat{\underline{\mathbf{X}}}{\text{Rx}}^* + \hat{\beta}{\text{Rx}}^*\hat{\mathbf{X}}_{\text{Rx}}. \tag{27} YRx∗=α^Rx∗X^Rx∗+β^Rx∗X^Rx.(27)
结合两者可得出估计的频域数据 X^Rx\hat{\mathbf{X}}{\text{Rx}}X^Rx(对于 ∣α^Rx∣2−∣β^Rx∣2≠0|\hat{\alpha}{\text{Rx}}|^2 - |\hat{\beta}_{\text{Rx}}|^2 \neq 0∣α^Rx∣2−∣β^Rx∣2=0)
X^Rx=1∣α^Rx∣2−∣β^Rx∣2(α^Rx∗YRx−β^RxY‾Rx∗).(28) \hat{\mathbf{X}}{\text{Rx}} = \frac{1}{|\hat{\alpha}{\text{Rx}}|^2 - |\hat{\beta}{\text{Rx}}|^2} \left( \hat{\alpha}{\text{Rx}}^*\mathbf{Y}{\text{Rx}} - \hat{\beta}{\text{Rx}}\underline{\mathbf{Y}}_{\text{Rx}}^* \right). \tag{28} X^Rx=∣α^Rx∣2−∣β^Rx∣21(α^Rx∗YRx−β^RxYRx∗).(28)
随后,经过 IQ 不平衡补偿的信道 H^\hat{\mathbf{H}}H^ 通过下式计算
H^=X^Rx⊘Y^Tx.(29) \hat{\mathbf{H}} = \hat{\mathbf{X}}{\text{Rx}} \oslash \hat{\mathbf{Y}}{\text{Tx}}. \tag{29} H^=X^Rx⊘Y^Tx.(29)
图 6 展示了经过 IQ 不平衡补偿后的信道的 RDM。为此,以混合复数/实数值双线性 LMS 滤波器(the mixed complex-/real-valued bilinear LMS filter)为例,用于估计 IQ 不平衡补偿所需的参数。该估计过程基于受 IQ 不平衡影响的信道中的两个最主导的峰值。与图 3b 相比,本底噪声大幅降低,然而,虚假目标仍然可以识别。正如 [12] 中所论证的,这些虚假目标可以通过跟踪算法进行识别和消除。
假设只有一个自由度,且 λ\lambdaλ 是复数
x^k=rk⋅λ∗∣α∣2−λ∣β∣2∣λ∣2(∣α∣2−∣β∣2)⏟信号发生畸变+r−k∗⋅α∗β(λ∗−λ)∣λ∣2(∣α∣2−∣β∣2)⏟镜像干扰残留\hat{x}k = \underbrace{r_k \cdot \frac{\lambda^* |\alpha|^2 - \lambda |\beta|^2}{|\lambda|^2 (|\alpha|^2 - |\beta|^2)}}{\text{信号发生畸变}} + \underbrace{r_{-k}^* \cdot \frac{\alpha^* \beta (\lambda^* - \lambda)}{|\lambda|^2 (|\alpha|^2 - |\beta|^2)}}_{\text{镜像干扰残留}}x^k=信号发生畸变 rk⋅∣λ∣2(∣α∣2−∣β∣2)λ∗∣α∣2−λ∣β∣2+镜像干扰残留 r−k∗⋅∣λ∣2(∣α∣2−∣β∣2)α∗β(λ∗−λ)其中 rk=ck,m(αsk+βs−k∗)r_k=c_{k,m}(\alpha s_k+\beta s_{-k}^*)rk=ck,m(αsk+βs−k∗)